A formula for the number of spanning trees of a multi-star related graph

(1)

Informqtion

y$gwl

Information Processing Letters 68 (1998) 295-298

A formula for the number of spanning trees of

a multi-star related graph

Wen-Ming Yan a,1, Wendy Myrvold b,2, Kuo-Liang Chung ‘,*

a

Department of Computer Science and Information Engineering, National Taiwan University, Taipei, Taiwan 10764 b Department of Computer Science, Universi@ of Victoria, PO. Box 3055, STN CSC, Victoria, BC, Canada V8W 3P6

’ Department of Information Management and Institute of Information Engineering, National Taiwan University of Science and Technology, No. 43, Section 4, Keelung Road, Taipei, Taiwan IO672

Received 1 July 1998; received in revised form 1 October 1998 Communicated by S.G. Akl

Abstract

Using a new labeling technique and matrix computations, this paper derives a closed formula for the number of spanning trees of a multi-star related graph G = Kn - Km(al, ~22, . . , a,), where Km(al, q, . . , am) consists of m star graphs such that the ith one has a root node connected to ai leaves, and further, the m roots are connected together to form a complete graph. This result generalizes the previous result by Nikolopoulos and Rondogiannis (1998) which is limited to m = 2,3,4. 0 1998 Elsevier Science B.V. All rights reserved.

Keywords: Combinatorial problems; Spanning trees; Multi-star graph

1. Introduction

An undirected graph G consist of a set V(G) of vertices and a set E(G) of edges where each edge corresponds to an unordered pair of vertices from

V(G). All graphs considered in this paper are simple

(they have no loops or multiple edges), finite, and undirected.

A complete graph on n vertices, denoted K,, has one edge between each pair of distinct vertices. The

complement G of a simple graph G = (V, E) on n

* Corresponding author. Email: klchung@cs.ntust.edu.hv. Sup- ported by NSC88-2213-EOI l-005/006.

’ Email: gauboon@csie.ntu.edu.tw. Supported by NSC87-2119- MOO2-006.

* Email: wendym@csr.uvic.ca. Supported by NSERC.

vertices is the n-vertex graph containing exactly the edges of K, which are not in G.

A multi-star related graph, G = K,, - K, (al, a2, . . . , a,), is an n-vertex graph whose complement consists of Km with vertices labeled ~1, ~2, . . . , urn, plus there are ai vertices of degree one (leaves) incident to vertex ui of the K,, and the remaining

k = n - m - al - a2 - . . . - a, vertices are isolated

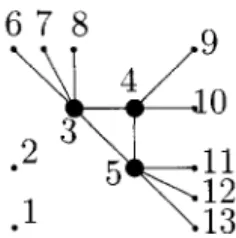
points. Fig. 1 illustrates a triple-star graph K3(3,2,3). Recently, using matrix computations, Nikolopoulos and Rondogiannis [3] derived a closed form for the number of spanning trees of multi-star related graphs G = K, - K,(al, a2, . . . , a,) for m = 2,3,4.

Surprisingly, some previous closed forms [ 1,2,4,5] for counting the number of spanning trees of some special graphs are covered in their result.

(2)

296 W-M. Yan et al. /Information Processing Letters 68 (1998) 295-298

Fig. 1. K3(3,2,3)

Using a new labeling technique and matrix computations, this paper derives a closed formula for the number of spanning trees of G = K, - Km (al, a2, . . . . a,) for arbitrary m. This extends the previous result [3] which is limited to m = 2,3,4.

2. Counting spanning trees

The complement spanning tree matrix [5] C for a graph G is defined by

Cij = i

n-di ifi=j, eij ifi#j,

where di is the degree of vertex i in G and eij is one if (i, j) is in E(G) and 0 otherwise.

The following result first derived by Temperley [5] provides a formula for the number of spanning trees of a graph. The notation ] C ] represents the determinant of matrix C.

Theorem 1 [5]. For the graph G, the number of spanning trees ofG, r(G), is equal to (l/n2)1CI.

This is applied in the next sections to derive a closed formula for the number of spanning trees of a multi- star related graph.

3. The generalization

In this section, a new approach to labeling the graph G is presented first. Then the closed form for counting the number of spanning trees of G for arbitrary m is given.

3.1. The new labeling method

Given the graph G = K, - K,,,(al, ~2, . . . , a,), the labeling method used by Nikolopolous and Ron- dogiannis [3] is to label the nodes in V(K,) -

Fig. 2. Labeling the complement graph of K13 - K3(3,2,3) [3].

V(K,(al,az,...,

a,)) first, then they label the nodes in the first star graph with at + 1 nodes. Finally, they label the nodes in the mth star graph with a, + 1 nodes. Therefore, using their labeling method, the labeling of the complement of K13 - K3(3,2,3) is shown in Fig. 2. In addition, the complement spanning tree matrix of Kt3 - K3(3,2,3) is given by

c=

wheren=13,m=3,and D= p11111 1 1 a 1 a 1 a 1 _{P2 11} ₁ 1 a 1 a \ 1 P3 11 1 1 a 1 a 1 a InmatrixD,a=n-1=12andpi=n-ai-m+ l=ll_Uiforl<i<3.

Our labeling method for G = K,, - K, (a,, ~22, . . . , a,) is to label the nodes in V(K,) - V(K,(al,az,

. . . , a,)) first, secondly to label the roots of the m star graphs. Then we label the nodes in the first star graph except the root node, and so on. Using the same graph as shown in Fig. 2, the new labeling is shown in Fig. 3.

(3)

WM. Yan et al. /Information Processing Letters 68 (1998) 295-298 297

Fig. 3. The new labeling of the vertices of K13 - K3 (3,2,3).

The complement spanning tree matrix corresponding to the graph as labeled in Fig. 3 is given by

C= but now D= p] 11111 1 P2 1 1 1 1 1 P3 1 a 1 a 1 a a 1 1 1 a a a a

The values of pi and a are as defined before.

Our new labeling method transforms the matrix D into a kite form. This simplifies the algebra involved in determining a closed formula for the number of spanning trees of G = K, - K,(u~,u~,...,u,) for arbitrary m .

r(G) = .k-2 * (n - l)a’+a2+...+am[1 + l/(ql - 1) + l/(q2-1)+...+ll(qm-l)l(qI-l)(q2-1)...(q,-

1) where qi = n - ui - m + 1 - ui/(n - l), and

k=n-m-ul-u2--..--ua,.

Proof. If the graph is labeled by the new method as described in the previous section, then the complement spanning tree matrix of G is given by

C=

wherek=n-m-at-uz-.-.-u,andthematrix

D is of a kite form and is written as

D= 1 ‘.. 111 p2 ‘.. : 1 “’ 1 pm a a 1 1 1 1 1 1 1 1 1 a a a 1 1 ‘.’ 1 a a a a

3.2. The closed formula

The next theorem gives our new formula. The proof involves algebraic manipulations of the complement spanning tree matrix which are facilitated by use of the new labeling scheme described in the previous section. Theorem 2. The number of spanning trees of a multi-

star related graph G = Kn - K,(ul, ~22, . . . , a,),

where a = n - 1 and pi = n - ui - m + 1 for 1 <

i < m. By Theorem 1, the number of spanning trees is rPID[.

To simplify the computation of the determinant of

D, we first zero out the ones in columns 1 to m which occur in the rows indexed by m + 1 or higher as follows: the one in row i is zeroed out by adding - 1 /(n - 1) times column i This affects only the main diagonals in the first m columns of the matrix.

(4)

298 W-M. Yan et al. /Information Processing Letters 68 (1998) 295-298

The matrix now has an m by m block which we label Q in the upper left hand comer with ones on the off-diagonal and diagonal entries qi = it - ai -

m + 1 - Ui/(n - 1). In columns 1 to m, the entries in

the rows indexed m + 1 or more are all zeroes. The determinant of D equals (n - l)crlfa2+-..+am 1 Q 1.

The matrix Q has diagonal elements ql,q2, . . . , qm and has ones on the off-diagonal. Border this matrix by adding a new first row and column. All the entries in the new row are ones. The entries in the new column which are not in the new row are zeroes. From expanding about the new column, it is clear that this new matrix has the same determinant as Q.

Subtract the new row from each of the other rows. The diagonal entries in the old row indexed i are now qi - 1. The first column has all -1’s except for the one in the first row. The first row is all ones. The remaining elements of the matrix are zero. Now add to the first column l/(qi - 1) times each of the other columns to zero out the off-diagonal entries in this column. The entry in the first row and column becomes 1+ l/(ql - 1) + l/(q2 - 1) +...+ l/(qm - 1). Also, the matrix is now upper triangular, so the determinant is: [l + l/(ql - 1) + l/(q:! - 1) + ... + l/(qm -

l>lh -

])(q2 - ]>...(qn? - 1).

In summary, t(G) is equal to nkp21DI. But IDI is equal to (n - l)‘l+‘~+“‘+‘~~ 1 Ql Further, ] QI = [ 1 + ]/(q1 - 1) + l/(92 - 1) + ... + l/(&r -

l)l(q1 -

])(q2 - ])*..(qrrl - 1). Thus, r(G) = nk-2(n- 1) “+a2+...+am[1 + l/(qt - 1) + l/(qz - 1) + . . . + l/(q,-l)l(qt-l)(q2-l)...(qm-l)asrequired. q 4. Conclusion

We have described how to derive the closed form for the number of spanning trees of a multi-star related graphG=K,-K,(at,a2,...,a,)forarbitrarym.

Our new labeling method transforms the complement spanning tree matrix G into matrix whose left-upper submatrix is an identity matrix and whose right-lower submatrix is of a kite form that makes the derivation of the closed form easier. The main contribution of this paper is that based on our new labeling method, the proposed closed form for arbitrary m generalizes the result of Nikolopoulos and Rondogiannis [3] whose closed form is limited to m = 2,3, and 4.

References

[l] C. Berge, Graphs and Hypergraphs, North-Holland, Amster- dam, 1973.

[2] W. Moon, Enumerating labeled trees, in: F. Harary (Ed.), Graph Theory and Theoretical Physics, Academic Press, London, 1967, pp. 261-271.

[3] SD. Niiolopoulos, P. Rondogiannis, On the number of spanning trees of multi-star related graphs, Inform. Process. Len. 65 (1998) 183-188.

[4] P.V. O’Neil, The number of trees in a certain network, Notices Amer. Math. Sot. 10 (1963) 569.

[5] H.N.V. Temperley, On the mutual cancellation of cluster inte- grals in Mayer’s fugacity series, Proc. Phys. Sot. 83 (1964) 3- 16.