Wave Propagation Analysis and Application of the Phononic Crystal with Defect Inserts

Wave propagation analysis and application of the phononic crystal

with defect inserts

Jia-Yi Yeh

Department of Information Management, Chung Hwa University of Medical Technology

E-mail: yeh@mail.hwai.edu.tw

Abstract

The wave propagation characteristics of the selective phononic crystals (PCs) with and without defect inserts are calculated in this investigation. According to the characteristics of the band gaps of the phononic crystals, it can be used to design some new type of wave filter devices. The wave propagation characteristics of the PCs are investigated and a detailed analytic model also developed to study the band structures of the phononic crystal system. In this paper, the experimental results are measured and compared with the numerical results. Based on the above investigations, we can design a series novel and tunable acoustic devices.

Keywords: Phononic crystal, Plane-wave-expansion, Band gap, Wave propagation

1. Introduction

The Phononic crystals (PCs) have unique characteristics named “phononic band gaps” (PBGs) within certain acoustic frequency. In PBGs, sound and vibrations in the PCs structure are forbidden, and those structures exhibit unique dynamic characteristics that make them act as mechanical filters for wave propagation. PCs named acoustic/sonic band gap media are the elastic analogues of photonic crystals and have also received renewed attention recently in Vasseur et al. [1] and Kuang et al. [2].

In recent years, extensive works have been done on analyzing the propagation of the elastic wave About the PCs. The PBGs were investigated theoretically by Kushwaha et al. [3] and experimentally by Vasseur [4] in composite systems constituted by periodic inclusions of a given material in a host matrix. Several theoretical methods such as, the plane-wave expansion (PWE) method, the finite difference time domain (FDTD) method and the multiple-scattering theory (MST) have been used to calculate the dynamic characteristics for wave propagation in many media of the PCs. The PWE method is most extensively used to calculate band structure among these methods because of its convenience. Kushwaha and Halevi [5] used the PWE method to investigate the characteristics of the periodic phononic system. Then, Caballero et al. [6] also used the PWE method to obtain larger gaps when they added a different size rod at the centre of each unit cell of square and honeycomb lattices.

Then, the PWE method was adopted by Hou et al. [7] to investigate the characteristics of the elastic wave in the periodic structures. The convergence problem of PWE method for phononic crystals was studied by Cao et al. [8]. Afterwards, Yeh [9] used the PWE method to calculate the variations of the band structure of the periodic structures with smart materials and controlled the wave propagation characteristics of the PCs by applying various electric fields. Kafesaki, Economou [10] studied the characteristics of periodic acoustic composites by using multiple-scattering theory, and Lai et al. [11] studied the acoustic band gaps problems by multiple scattering theory. According to the above references, it is convenient to calculate the band structures of periodic phononic system by ©2007 National Kaohsiung University of Applied Sciences, ISSN 1813-3851

PWE method.

In this study, the band structures of the PCs with different combination types with and without defect inserts are calculated, respectively. Applications of the PCs with the designed defects are presented and the PWE method is employed to analyze the feature of elastic wave equations and calculate the variations of the band gaps of the PCs. Additionally, the experimental results of the PCs system are measured and compared with the numerical results. According to the above investigations, a series tunable and active control acoustic device can be designed and utilized. The investigation in this paper hopes to provide the based guidelines to design the novel PCs system and more effective and tunable filtering characteristics in the future work.

2. Analytical Model and Calculation Method

In this paper, the band structure of the one-dimensional PCs system is modeled and calculated. The general vibration equation of the one-dimensional rod composites is shown as follows:

] ) ( ) ( [ ) ( ) ( 2 2 x u x A x E x t u x A x ∂ ∂ ∂ ∂ = ∂ ∂ ρ ₍₁₎

where ρ(x), , are the mass density, Young’s modulus, and sectional area, respectively. Generally, the mass density, Young’s modulus, and sectional area are constants for the homogeneous material. So, the equation (1) can be written as the general one-dimensional wave propagation equation form:

) (x E A(x) 2 2 2 2 2 x u c t u ∂ ∂ = ∂ ∂ (2)

in which,

c

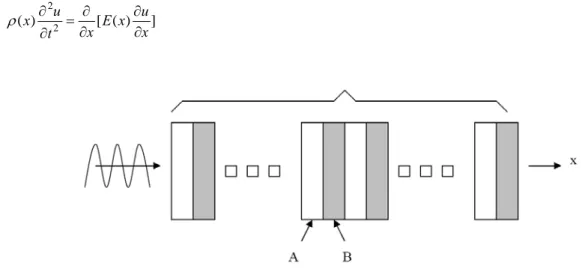
is the transverse speed of acoustic wave.

As shown in Fig.1, we suppose that the one-dimensional PCs consist of the material A with the width , the material B with the width , and the lattice spacing is

1

a

1

b a=a1+b1. Then, the equation (1) can be rewritten as follows: ] ) ( [ ) ( 2 2 x u x E x t u x ∂ ∂ ∂ ∂ = ∂ ∂ ρ (3)

Then, the mass density and Young’s modulus can be expanded as Fourier series and shows as the following equations for periodic composites:

∑

⋅ = G x iG e G x) ( ) ( ρ ρ (4)

∑

⋅ = G x iG e G E x E( ) ( ) ₍₅₎

where G is the reciprocal-lattice vector.

In this study, the mass density and Young’s modulus of the material A and B are ρ , A ρ , B , and ,

respectively. Therefore, the Fourier coefficients in equation (4) and (5) now take a particular simple form as follows: A E EB ⎪⎩ ⎪ ⎨ ⎧ ≠ − − = + = − 0 , / ) 1 )( ( 0 , / ) ( ) ( 1 1 G a e G a b a G _iGa B A B A ρ ρ ρ ρ ρ (6) ⎪⎩ ⎪ ⎨ ⎧ ≠ − − = + = − 0 , / ) 1 )( ( 0 , / ) ( ) ( 1 1 G a e E E G a E b E a G E _iGa B A B A (7)

In order to satisfy the Bloch theorem, the displacement u( tx, ) can be presented as follows:

) ( ) , (xt e( )u x u = ikx−ωt k (8)

and equation (8) can be rewritten as the following form:

∑

+ − = 0 0 _{( )} ) , ( ( ) ₀ G k kx x G i iωω _{e u G} e t x u ₍₉₎

in which, ( ) ( 0), is the Bloch wave vector, and 0 0 u G e x u _k G x iG

k =

∑

_{k ω is the circular frequency of the wave.}

Then, we substitute the equation (4), (5), and (9) into equation (3) and yield the following form:

∑

′− =

∑

+ ′+ ′− 0 0 ) ( ) )( ( ) ( ) ( ) ( _{0 0 0 0 0} 2 G G k k G G G u G G k G k E G G u ρ ω ₍₁₀₎ where G′=G+G0.

This is a set of linear, homogeneous equations for the eigenvector u_k(G) and eigenfrequency ω(k), if G is permitted to take all the possible values. Thus, the Band structures of the PCs can be obtained and calculate by scan the area of the irreducible region of the Brillouin zone.

3. Results and Discussions

The characteristics of the wave propagations of the selective PCs were calculated in this paper. The material A and B are aluminum and PMMA in the PCs as shown in Fig.1. In this study, the 1-D PCs consist of alternative stacking of aluminum and PMMA planar sheets, which have the same dimensions. The dimensions and material properties of the material A and B are listed in Table 1. Additionally, the used defects (described as material C) in this paper are aluminum and the relative properties are also listed in Table 1.

Table 1. Material properties of the PCs system

Material A (Al) Material B (PMMA) material C

thickness 3 mm 3 mm 1 mm

mass densities 2700kg/m3 1185kg/m3 2700kg/m3

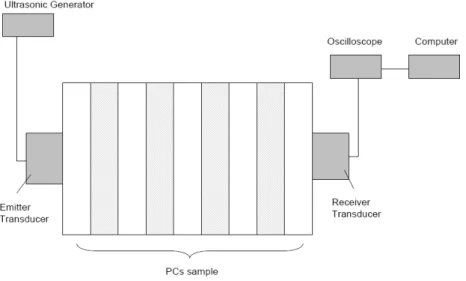
The experiments are adopted to validate the accuracy of the numerical results and the experimental configuration is shown in Fig. 2.

Figure 2. Experimental configurations of phononic crystal system.

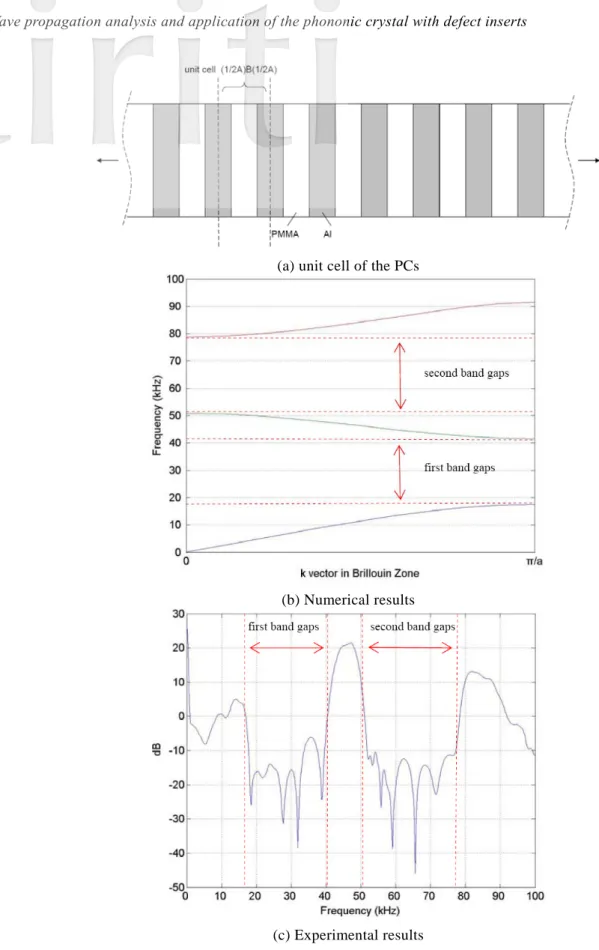
The numerical results of the PCs without defect are presented in Fig. 3(a) and (b), respectively. For this case, the experimental setup of the PCs has the stacking of five unit cells (the unit cell is (1/2A)B(1/2A)). It can be observed that the locations and widths of the band gaps of the PCs according to the numerical results. Additionally, Fig. 3(c) shows the experimental results of the present PCs system and it shows that numerical and experimental results have good agreement for the first two band gaps.

(a) unit cell of the PCs

(b) Numerical results

(c) Experimental results

Figure 3. The numerical and experimental results of PCs without defect inserts.

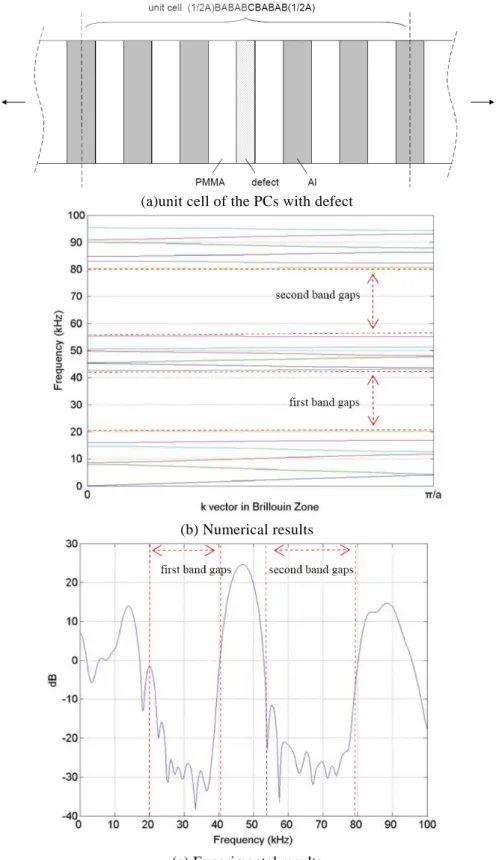
In Fig. 4, the numerical and experimental results of the PCs with designed defect insert are calculated and measured. In this case, the unit cell of the PCs with defect insert is presented as Fig. 4(a). The numerical results are plotted in Fig. 4(b). Additionally, in order to validate the numerical results, the experimental results are measured by the setup of stacking for one unit cells ((1/2A)BABABCBABAB(1/2A)). The experimental results of

this case are shown in Fig. 4(c) and there is only one defect in this experimental configuration. According to the results, the first two band gaps (about 20-42 kHz and 55-80 kHz) characteristics can be found in the experimental results. And, the band gaps also have better effect in filtering the acoustic wave compared with the results in Fig. 3.

(a)unit cell of the PCs with defect

(b) Numerical results

(c) Experimental results

From the above numerical and experimental results, it can be seen that we can design the PCs by combining different types of materials. We also can get some to get some specific-effect acoustic filters, such as high-effect or tunable acoustic wave filters by adding defect inserts in the phononic crystal system.

4. Conclusions

Unique characteristics of the wave propagation in PCs with and without defect are investigated in this study. The characteristics of the wave propagations of the PCs with selective defect were analyzed and applied to design a new type of filter according to the characteristics of the band gaps of the PCs in this paper.

According to above numerical and experimental results, it can be observed that we can filter the certain bands of frequencies by choosing a suitable periodic system. By adding a defect in the periodic system, the band gaps can be changed. Based on the experimental results, it can be observed and validated that the added defects also affect the location and width of the band gaps of the PCs and different defect will influence the wave propagation properties of the PCs system. Thus, we can achieve the specific filters of the PCs by the way of the combination with different materials and defects.

Acknowledgements

This research was partially supported by the National Science Council in Taiwan through Grant NSC 96-2221-E-273-009-MY3.

Reference

[1] Vasseur J.O., Djafari-Rouhani B., Dobrzynski L., Kushwaha M.S. and Halevi P., “Complete acoustic band gaps in periodic fibre reinforced composite materials: the carbon/epoxy composite and some metallic systems,” Journal of Physics: Condensed Matter, Vol.6, pp. 8759-8770, 1994.

[2] Kuang W., Hou Z. and Liu Y., “The effects of shapes and symmetries of scatterers on the phononic band gap in 2D phononic crystals,” Physics Letters A, Vol. 332, No. 5-6, pp. 481-490, 2004.

[3] Kushwaha M.S., Halevi P., Dobrzynski L. and Djafari-Rouhani B., “Acoustic band structure of periodic elastic composites,” Physical Review Letters, Vol. 71, pp. 2022-2025, 1993.

[4] Vasseur J.O., Deymier P.A., Frantziskonis G., Hong G., Djafari-Rouhani B. and Dobrzynski L., “Experimental evidence for the existence of absolute acoustic band gaps in two-dimensional periodic composite media,” Vol. 10, pp. 6051-6064, 1998.

[5] Kushwaha M.S. and Halevi P., “Giant acoustic stop bands in two-dimensional periodic arrays of liquid cylinders,” Applied Physics Letters, Vol. 69, No. 1, pp. 31-33, 1996.

[6] Caballero D., Sanchez-Dehesa J., Rubio C., Mártinez-Sala R., Sánchez-Pérez J.V., Meseguer F. and Llinares J., “Large two-dimensional sonic band gaps,” Physical Review E, Vol.69, No. 6, pp. R6316-R6319, 1999.

[7] Hou Z., Fu X. and Liu Y., “Acoustic wave in a two-dimensional composite medium with anisotropic inclusions,” Physics Letters A, Vol. 317, No. 1-2, pp. 127-134, 2003.

[8] Cao Y., Hou Z. and Liu Y., “Convergence problem of plane-wave expansion method for phononic crystals,” Physics Letters A, Vol. 327, No. 2-3, pp. 247-253, 2004.

[9] Yeh J.Y., “Control analysis of the tunable phononic crystal with electrorheological material,” Physica B: Physics of Condensed Matter, Vol. 400, No. 1-2, pp. 137-144, 2007.

[10] Kafesaki M. and Economou E.N., “Multiple-scattering theory for three-dimensional periodic acoustic composites,” Physical Review B, Vol. 60, No. 17, pp. 11993-12001, 1999.

[11] Lai Y., Zhang X. and Zhang Z.Q., “Engineering acoustic band gaps,” Applied Physics Letters, Vol.79, No.20, pp. 3224-3226, 2001.