The minimum spanner problem on butterfly graphs

The Minimum Spanner Problem on Butterfly Graphs

Shien-Ching Hwang and Gen-Huey Chen

Department of Computer Science and Information Engineering, National Taiwan University, Taipei, TA1 WAN

Email: ghchen@csie.ntu.edu.tw

Abstract

Given a connected graph G, a spanning subgraph G' of G is called a t-spanner

if every

pair of two adjacent vertices in G has a distance of at most t in G! A t-spanner of a

graph G is minimum

if

it contains minimum number of edges among all t-spanners of G. Finding minimum spanners for general graphs is rather difzcult. Most of previous results were obtained for some particular graphs,

e.g., butterfly graphs, cube-connected cycles, de Bruijn graphs, Kautz graphs, complete bipartite graphs, and permutation graphs. The butterfly graphs were originally introduced as the underlying graphs of FFT networks which can perform the fast Fourier transform (FFT) very eficiently. In this paper, we successfully construct most of the minimum t-spanners for the k-aiy r-dimensional butterfly graphs for 2 I t I 6 and t = 8.

1 Introduction

The notion of spanners was originated from constructing synchronizers that are used to transform synchronous algorithms into asynchronous ones [6]. Given a connected graph G, a spanning subgraph G' of G is called a t-spanner if d(u, v) I t in G' for every edge (U, v) of G, where d(u, v) is the distance between U and v. Further, a t-spanner G' is proper if it is a proper subgraph of G, and minimum if it contains minimum edges among all t-spanners of G. A t-spanner is a tree t-spanner if it forms a tree. A tree t-spanner must be a minimum t-spanner. A t-spanner is also a t'-spanner for t' > t. G is a t-spanner of itself for t 2 1.

Finding minimum spanners, in general, is very difficult.

It was shown in [7] that fmding a minimum t-spanner of an arbitrary graph for t 2 2 is NP-hard. It remains NP-hard even if the graph is of bounded degree (see [l]). Thus far, minimum t-spanners have been obtained for some particular graphs, e.g., butterfly graphs (2 I t I 7) [2, 31, cube-connected cycles (2 I t I 7) [3], de Bruijn graphs (t = 2, 3) [2, 31, Kautz graphs (t = 2, 3) [2], complete bipartite graphs (t = 3) [5], and permutation graphs (t = 3) [5].

For convenience we use BF(k, r) to denote an

r-dimensional k-ary butterfly graph. A formal definition of BF(k, r) is given in the next section. Heydemann et al. [3] first constructed a minimum 2-spanner of BF(2, 3) that contains 40 edges, a minimum 3-spanner of BF(2, r) that contains 3r2'-' edges for r 2 5, a minimum f-spanner of BF(2, r) that contains (3r

-

1)2F-' edges for 3 I r I 7 and max(3, r

-

1 } I t I 6, and a minimum 7-spanner of BF(2, r) that contains 5r2'-2 edges for r 2 9. However, their results are not correct for 4 I t I 6 and 3 I r I t

-

1. Then, Harbane and Padld [2] constructed minimum 3-spanners of BF(k, r) that contains (2r

-

l)kpl edges for r 2 5. In this paper, we construct a minimum t-spanner of BF(2, r) that contains ((2r

-

1)k

-

r)K' edges for 4 I t I 6 and r = t

-

2 or t

-

1, a minimum t-spanner of BF(k, r) that contains (2k

-

l)rkF-' edges for 3 I II 6 and ( k = 2 and r 2 t

+

2 or k 2 3 and r 2 t), and a minimum 8-spanner of BF(k, r) that contains 52" edges for r 2 10 even. Moreover, an (r

+

1)-spanner of BF(k, r) that contains ((2r

-

l)k

-

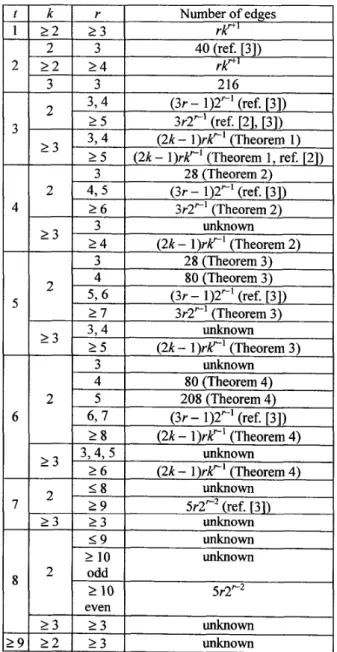
r)klL1

edges is constructed as well. We show in Table I the current status of the minimum t-spanners for BF(k, r).

2

Preliminaries

There are r levels, numbered 0, 1,

...,

r

-

1, associated with BF(k, r). Each level contains Y vertices that are labeled with

V k-ary sequences of

r symbols. A vertex of level 1 labeled with

flo~l-ppl

is represented with <1,

p0p1-ppI>,

where 0 I 1 I r-1 and 0 I

p,

I k

-

1 for all 0 I

j I r

-

1. Each vertex 4,

popl- pPl>

is connected to 2k vertices: <I

-

1, pop1-$-2i/3,--ppl> and

<I

+

1, ~ o ~ I . - p ~ - . l i

p/+~.-p,$

for all 0 I i I k

-

1. Throughout this paper, all arithmetic computations whose operands are the symbols and the levels are performed modulo k and modulo r, respectively. A formal definition of BF(k, r) is as follows.

Definition 1. The vertex set of BF(k, r) is {<Z,

po/31-.&l>

1

O l l l r - 1 a n d O I ~ , I k - l f o r a l l O I j ~ r - l ) . T h e edge set of BF(k, r) is {(4,

p0p1-.prl>,

<I

+

I ,

p',,p'l.-

p',.-1>)lOIl<r- 1 a n d h = p ' , f o r a l l O I j I r - 1 a n d j # l } . (4, /.?0pI--pp1>,

<I

+ 1,

p',,p'l.-.p',$)

is referred to as

an i-edge if

p'/

= + i, where 0 I i I k

-

1. An i-edge is firther called a straight edge if i = 0, and a skew edge if i # 0.

and rk*' edges contained in BF(k, r). The edges exist between adjacent levels. Level 0 and level r

-

1 are considered adjacent. Hence, BF(k, r ) with even r is a bipartite graph. Since BF(R, 1) and BF(1, r) have trivial structures and BF(k, 2) is a multigraph, we consider BF(k, r ) with k 2 2 and r 2 3 in this paper. The structure of BF(3, 3) is depicted in Figure 1 , where level 0 is replicated. BF(k, r) thus defined was named wrapped butterfly graphs in [4].

Given 4, /30P1-.Pr-1>, the subgraph of BF(k, r ) induced

by {<l,

PoPI-P/-~(P/

+

i)fi/+l-Pr-l>

I

0 I i I k

-

l } u

{<Z

+

1,

PoPI-.P,-I@/

+ i)P/+l-.Pr-I> I O I i I k

-

1) is a complete

bipartite graph with two partite sets of size k. In terms of

graph notations, the subgraph is a Kk,k. In this paper we consider the subgraph a basic module of BF(k, r). Three basic modules of BF(3, 3) are shown with bold edges in Figure 1. The following three observations are about the basic module.

Observation 1. The edge set of BF(k, r) can be partitioned into rK"' basic modules.

Observation 2. Suppose U is a vertex in BF(k, r), and v, w

are two vertices of the same level that are adjacent to U.

Then, U, v, and w belong to the same basic module. Observation 3. Two distinct basic modules are vertex-disjoint or have one vertex in common.

A cycle in BF(k, r) is referred to as an i-cycZe if its edges are all i-edges. For example, (<O, OOO>, 4 , OOO>, <2, OOO>, <3,000>, <O, OOO>) is a 0-cycle in BF(3, 3) and (<O,

ooo>,

4 , loo>,

a,

110>,

<o,

111>, <1, 211>, (2, 221>, <O, 222>, < I , 022>, <2,002>, <O, OOO>) is a 1-cycle in BF(3, 3). Each 0-cycle in BF(k, r ) contains r straight edges and each 1-cycle in BF(k, r) contains kr skew edges. There is no skew edge in 0-cycles, and there is no straight edge in 1-cycles.

In [ 5 ] , Madanlal et al. constructed a tree 3-spanner of a the two partite sets of the Kk,k. The tree 3-spanner contains edges ( x l , y,), (x,, f i ) for 1 I i I k and 2 I j I k. According to Observation 1, a spanning subgraph of BF(k, r ) can result if the tree 3-spanner is constructed for each basic module. We use Sk,r to denote the resulting spanning subgraph. Clearly, Sk,r contains (2k

-

1)rKl edges. Since a 3-spanner is also a t-spanner for t 2 3. We have the following lemma.

Lemma 1. sk,r is a t-spanner of BF(k, r) for t 2 3.

Kk,k. SUppOSe x = { X l , X2,

...,

X k } and Y = b l , y2,

...,

yk} are

Let Tk,r be a spanning subgraph of BF(k, r ) whose edge set is {(<O, aaP~-P,-l>, <I, P 0 ~ P 2 - . P P 1 > )

I

a,

PO,

P27

...)

PPI€ { O , 1,

...)

k

-

l}} U {(Cl, a0lp2.-pr-1>, <2, ap1p2.-

Pr-1>)

I

a,

PI,

P 2 , a . . , PP1 E (0, 1, a . . , k - 11 and

a+

P I > U

{(<l, pop1.-pr-1>, <2, POPl.~$%-l>)

I

Po, P1,

... ,

Pr-1 E (0,

1,

...,

k - l } and Po f P i } U

{(<k

PoP1...&1>, <E + 1,

POPl...Pr-l>>

I

Po,

P1, . a - , Pr-1 E (0, 1, e.., k - 11 and (2,

3,

. . .,

r

-

1)

I

U

((4,

POD1 -.D/-lOP/+l--D*l>,

<I

+

1,DoD1-

P/-lP/P/+l...Pr-l>)

I

Po,

P1,

-..,

Pr-1 E (0, 1, . * * Y k - 1 1 , 16 (2,

3,

. . .,

r

-

l}, and

PI

# 0 ) . Clearly, Tk,r contains ((27

-

1)k

-

r ) K 1 < (2k

-

1 ) r r ' edges, where (2k

- 1 ) r K '

is the number of edges in &,r. The 4-spanner shown in Figure 2 is

the graph T2,3. As explained below, Tk,r is an (r

+

1)-spanner of BF(k, r).

The edges of BF(k, r ) that are not contained in Tk,r can be classified into the following five classes: (1) (<O,

POPI.-

PPI>, <I, POPl*~.P?-l>), (2) (<O, POPl...Pr-l>, <I,

(Po

+

OPI

P2...Pr-l>), (3) (<I? POPOPZP3...Pr-l>, <2, POPObP3...Pr-l>),

(4) PO PI^-^>, <2,

W(P1

+ i)P2.-Pr-+), and ( 5 )

(4

PoP1-Pr-l>, <l + 1,

PoPI-.P/-I(PI

+ i)P/+1-Pr-?), where i E

c 1 7 2, e..> k - 11,

Po,

P1, a-.,

Pr-1

E (0, 1,

...,

k - 1 1 ,

I €

(2,

3,

. .

.,

r - 1 },

PO

#

PI,

and

fl,

f 0. Between both end vertices of each edge above, there is a path of length 5 (r

+

1) in S. The path can be constructed as (<O,

PoP1.-~r-l>,

<r

-

1,

Po

P1-.Pr-l>, <r

-

2, PoP1-Pr-l>,

...,

<I,

POPI-.PpI>)

for (I), (<O, P O P 1 -Pr-l>, <r

-

1, POpI-P,-1>, <r

-

2, P O P I - .

PH>,

...)

< I , P0P1-Pr-1>, <O, P1P1.-PP1>, <I, @O + j)P& ...Pr-l>> for

PoPoAP3.-Pr-1>,

<o,

P o P o ~ P 3 - ~ ~ P i - l > ,

<r - 1, PoPoP2P3.-Pr-1>, <r

-

2, POPoP2P3.-pr-l>,

. . .

, <2, P o

PO@I

+ i)b.-Pr-l>, <O, W(P1 + i)&-P,-l>, <r

-

1, P o (PI + i)P2

-P,-I>,

<r - 2, PO@^+ i)P2-Pr1>,

. . .

,

<2, Po@1

+ i ) P 2 + - 1 > ) for (4) ifPo=Pl+ i, (<I, P O P 1 4 . % - 1 > , <2, P O P 1

-.PA>,

<I,

POPO~~-..P,-~>,

<2, P o @ l + i)p2-.Pr-1>) for (4) if

Po

f

P1

+ i, and (<4 POPl...PPl>, + 1, POPl...Pr-1>, <l,

Po

Pl...P/-lOP,+1...Pr-l>,

<I

+ 1,

POP~.-P/-~@/

+ i)P/+1-Pr-I>> for

( 5 ) .

3 Minimum spanners

Since each 0-cycle in BF(k, r) has length r and there is no cycle of length three in BF(k, r) that contains skew edges, there is no proper 2-spanner of BF(k, r) for r 2 4 and there are minimum 2-spanners of BF(k, 3) which can be obtained by removing a straight edge from each 0-cycle. Each minimum 2-spanner of BF(k, 3) contains 3k4

-

k3

edges. In the rest of this section, minimum t-spanners of

BF(k, r ) for 3 I t I 6 are constructed.

3.1 Minimum 3-spanners

A minimum 3-spanner of BF(2, r ) was constructed in [3], which contains 3r2" edges if r 2 5 and (3r

-

1)2"-' edges if r = 3 or 4. In [2], Harbane and Pa& constructed 3-spanners of the complete generalized p-cycle graphs, which represent a family of underlying graphs produced by the conjunction of a directed cycle of length p with a de Bruijn digraph. They showed that BF(k, r ) belongs to the family of graphs and the 3-spanner is minimum for BF(k, r ) with r 2 5 . In the following, a minimum 3-spanner of BF(A, r ) for k 2 3 and r 2 3 is constructed.

Since the skew edges in a basic module of BF(k, r ) together form a connected spanning subgraph of the basic module, we have the following lemma.

Lemma 2. Suppose H i s a disconnected spanning subgraph

of a basic module of BF(k, r), where k 2 3. There is a skew edge in the basic module whose both end vertices belong to two distinct components of H.

Lemma 3. Every cycle of length I 4 in BF(k, r) is either a 0-cycle or contained in a basic module.

ProoJ Suppose (U, v, w, U) is a cycle of length three in BF(k, r). Without loss of generality, we assume lev(u)=l and lev(v) = 1

+

1, where 0 I 1 I r - 1 and lev(u) represents the level of vertex U. Then, lev(w) = I + 2. We have lev(u) = Iev(w)

+

1 or lev(w) - 1, which implies r = 3. Hence (U, v, w , U) is a 0-cycle in BF(k, 3).

On the other hand, suppose (U, v, w, x, U) is a cycle of length four in BF(k, r). We assume lev(u) = 1 and Iev(v) = 1

+

1, where 0 I E I r - 1. Then, Iev(w) = I o r I + 2 and lev(x)

= I

-

1 or I

+

1. If Iev(w) = land Iev(x) = I - 1, then U, v, and w belong to the same basic module and w, x, and U belong to the same basic module according to Observation 2. By Observation 3 the two basic modules are identical. Hence, (U, v, w, x, U) is contained in a basic module. The discussion is similar if lev(w) =

I

and Iev(x) =

I

+

1 or Iev(w) = I

+

2 and Iev(x) =

I +

1. If lev(w) = I + 2 and Iev(x) =

I-

1,

we have r = 4 because w and x are adjacent. It is easy to

0 Theorem 1. A minimum 3-spanner of BF(k, r), which contains (2k

-

l)rkpl edges, can be constructed, where k 2

3 a n d r 2 3 .

ProoJ We show that Sk,r is a minimum 3-spanner of BF(k,

r). By Lemma 1 s k , r is a 3-spanner of BF(k, r). sk,r is

minimum if every 3-spanner of BF(k, r) contains at least

(2k

-

1 ) r T ' edges.

Suppose S is a 3-spanner of BF(k, r), B is a basic module of BF(k, r), and B' is the subgraph of S induced by

the vertex set of B. B' is not necessarily a 3-spanner of B. We first show that every skew edge ( U , v) in B has d(u, v)

I 3 in B'. If (U, v) is an edge of S, then d(u, v) = 1 in B'.

Otherwise, there is a path of length I 3 between U and v in S. The path together with (U, v) forms a cycle of length I 4 in BF(k, r). Since there is no skew edge in 0-cycles, the cycle is contained in B according to Lemma 3. Hence, the path is contained in B', i.e., d(u, v) I 3 in B'.

Then we show that B' is connected. I f B' is disconnected, then Lemma 2 assures a skew edge (U', v') in B so that U' and v' belong to two distinct components of B',

which contradicts our discussion above. Hence, B' contains at least 2k

-

1 edges. By Observation 1 S contains at least

3.2

Minimum 4-spanners

Lemma 4. There is no cycle in BF(k, r) whose length is odd and smaller than r.

ProoJ: Suppose C is a cycle in BF(k, r) whose length is smaller than r. There exists a subgraph of BF(A, r) whose vertices are positioned at s consecutive levels so that C is contained in the subgraph, where s I r

-

1 is even. Since see that (U, v, w, x, U) is a 0-cycle in BF(k, 4).

(2k - 1)rT' edges. 0

the subgraph is bipartite, the length of C is even.

ProoJ Similar to the proof of Lemma 3.

0 Lemma 5. Every cycle of length five in BF(k, 5) is a 0-cycle.

0

Theorem 2. A minimum 4-spanner of BF(k, r), which contains (2k

-

l)rk'-l edges, can be constructed where k 2

3 and r 2 4 or k = 2 and r 2 6. A minimum 4-spanner of

BF(2,3), which contains 28 edges, can be constructed. Proof: We show that Sk,r is a minimum 4-spanner of BF(k,

r) for k 2 3 and r 2 4 or k = 2 and r 2 6. By Lemma 1 S,r is a 4-spanner of BF(k, r). Sk,r is minimum if every 4-spanner

of BF(k, r) contains at least (2k

-

1 ) r T ' edges.

Suppose S is a +spanner of BF(k, r), B is a basic module of BF(k, r), and B' is the subgraph of S induced by the vertex set of B. B' is not necessarily a 4-spanner of B. We first consider the situation of k 2 3 and r 2 4. For each skew edge ( U , v) in B, we have d(u, v) 5 3 in B' for the following reason. If (U, v) is not an edge of S, then there is a path of length I 4 between U and v in S. The path together with (U, v) forms a cycle of length I 5 in BF(k, r). By Lemma 4 there is no cycle of length three in BF(k, r). Also there is no cycle of length five in BF(k, r), as a consequence of Lemma 4, Lemma 5, and the fact that BF(k, 4) is bipartite. Consequently, the cycle has length four. By Lemma 3 the cycle is contained in B, which implies d(u, v)

I 3 in B! By the same argument as the proof of Theorem 1,

it can be proved that B' is connected and hence contains at least 2k

-

1 edges. By Observation 1 S contains at least (2k

-

1)rKC' edges.

Then we consider the situation of k = 2 and r 2 6. B' is

a 4-spanner of B for the following reason. If B' is not a 4-spanner of B, then there is an edge (U, v) in B so that d(u,

v) > 4 in B'. Since d(u, v) I 4 in S, there is a path of length I 4 between U and v in S. The path together with (U, v) forms a cycle of length I 5 in BF(2, r). The cycle is neither a 0-cycle nor contained in B. By Lemma 4 the cycle has length four, which contradicts Lemma 3. Since B is isomorphic to K2,2, B' contains at least 3 edges. By Observation 1 S contains at least 3r2" edges.

Next we consider the situation of k = 2 and r = 3. B is isomorphic to K2,2, which forms a cycle of length four, denoted by C4. If we remove a straight edge, say (4,

popl

p2>.

<I

+ 1, Pop&>), f?om a C4 and add two straight edges

popIp2>),

then a cycle of length five, denoted by Cs, results. For example, refer to Figure 2, where (<O, OOO>, <1, loo>, <O, loo>, <1,000>, <O, OOO>) is a C, and (<O, loo>, <1,

loo>,

<2, 1 lo>, <1, 1 lo>,

e,

loo>, <O, loo>) is a C5. As

explained below, the 4-spanner T2,3 shown in Figure 2 is minimum. We only need to show that S contains at least 28 edges.

Suppose ( ~ 1 , v l ) and (uZ, v2) are the two skew edges in B. It is not difficult to see that each cycle of length I 5 in BF(2,3) is a 0-cycle or a C4 or a C5. A 0-cycle contains no

skew edges. If a C4 (or a C5) contains one of ( u l , vl) and

(ut, v2), it also contains the other. Hence, S contains (U], vI) or (u2, v2), for otherwise there are no paths of length I 4 between u1 and v1 and between u2 and v2 in S. If S contains one skew edge of each basic module and two edges of each 0-cycle, then S contains 28 edges.

If there is a 0-cycle whose one edge is contained in S, then there are two basic modules whose skew edges are all contained in S. Hence, S contains at least 28

-

1

+

2 = 29 edges. This can be further explained as follows. Let us

consider (<O, OOO>, 4 , OOO>, <2, OOO>, <O, OOO>), which is the leftmost 0-cycle in Figure 2. Without loss of generality, we assume that the two edges (<O, OOO>, <I,

OOO>) and (<l, OOO>, <2, OOO>) are not contained in S. Then the two skew edges (<O, OOO>, 4 , loo>) and (<l,

OOO>, <O, loo>) are contained in S, for otherwise there are no path of length I 4 between <O, OOO> and < l,OOO> in S. Hence, (<O, OOO>, 4 , OOO>) can be "offset" with one of the two skew edges. Similarly, the two skew edges (<l, OOO>, <2,010>) and

(a,

OOO>, <1,010>) are contained in

S, and ( 4 , OOO>, <2, OOO>) can be "offset" with one of them. The discussion is similar if there is a 0-cycle whose

three edges are not contained in S. 0

3.3

Minimum

5-spanners

and

minimum

6-spanners

Lemma 6. Every cycle of length six in BF(k, r ) is either a 0-cycle or contained in a basic module, where r 2 5.

0

Theorem 3. A minimum 5-spanner of BF(k, r), which contains (2k

-

1)rkT' edges, can be constructed, where k 2 3 and r 2 5 or k = 2 and r 2 7. A minimum 5-spanner of BF(2, 3), which contains 28 edges, can be constructed. A minimum 5-spanner of BF(2, 4), which contains 80 edges, can be constructed.

Proof: By the aid of Observation 1, Lemma 1, Lemma 3, Lemma 4, Lemma 5 , and Lemma 6, it can be proved that Sk,r is a minimum 5-spanner of BF(k, r) for k 2 3 and r 2 5 or

k

= 2 and r 2 7. The proof is similar to the proof (for k 2 3 and r 2 4 or k = 2 and r 2 6) of Theorem 2. The 4-spanner T2,3 is a minimum 5-spanner of BF(2, 3), because every 5-spanner of BF(2, 3) contains at least 28 edges, as explained below.

Suppose S is a 5-spanner of BF(2,3) and (u1, V I ) , (242, v2) are two skew edges of a basic module. We first show that S

contains at least 12 skew edges. By Observation 1 there are 12 edge-disjoint basic modules. If S contains at least one skew edge of each basic module, then S contains at least 12 skew edges. We only need to consider the situation that neither of (ul, vl) and (ut, v2) is contained in S. It was shown in the proof of Theorem 2 that every cycle of length 2 5 in BF(2,3) that contains one of (U,, vl) and (uz, v2) also contains the other. Hence there are a cycle of length six that contains (ul, vl) but does not contain (ut, v2) and a Proof: Similar to the proof of Lemma 3.

cycle of length six that contains (u2, v2) but does not contain (ul, vl), both in BF(2, 3). The two cycles are 1-cycles, and they contain two skew edges of another basic module. One of (ul, vl) and (u2, v2) can be "offset" with one of the two skew edges. For example, consider (ul, vl)

Then (<O, 111>, 4 , 011>) and (<O, 011>, <1, ill>), which are two skew edges of another basic module, belong to the two 1-cycles that contain ( u l , vl) and (242, V Z ) , respectively. Refer to Figure 2. One of (U], vl) and (2.42, v2) can be "offset" with one of (<O, 11 I>, 4 , 01 1>) and (<O,

O l P , <1, 1 1 P ) . We say that both of (u1, VI) and (242, v2) and both of (<O, 11 1>, <1,011>) and (<O, 01 1>, 4 , 11 I>) are the dual of each other.

Without loss of generality, we assume that S contains 12 skew edges. There are eight edge-disjoint 0-cycles in BF(2, 3). If each 0-cycle has two edges contained in S,

then S contains 12

+

2 x 8 = 28 edges. It was shown in the proof of Theorem 2 that if there is a 0-cycle whose one edge is contained in S, then there are two basic modules whose skew edges are all contained in S. Since at least one of their dual skew edges is contained in S, one of the missing edges in the 0-cycle can be "offset" with one of the dual skew edges. For example, consider the leftmost 0-cycle (<O, OOO>, <1, OOO>, <2, OOO>, <O, OOO>) in Figure 2. If the two edges (<O, OOO>, 4 ,

OOO>)

and ( 4 , OOO>, <2, OOO>) are not contained in S, then the four skew edges (<O, OOO>, 4 , loo>), (<O, loo>, 4 , OOO>), ( 4 , OOO>, <2, 010>), and (<l, 010>, <2, OOO>) must be contained in S. Their dual skew edges are (<O, 011>, 4,

ill>), (<O, 111>, <1, 011>), (<l, 101>, <2, ill>), and ( 4 , 11 1>, <2, 10D). At least one of them is contained in S, for otherwise there is no path of length 1 5 between <O, 011> and 4, 111>. Hence one of (<O, OOO>, <1, OOO>) and ( 4 , OOO>, <2,000>) can be "offset" with one of (<O, 11 l>), and (<l, 11 I>, <2, 101>). The discussion is similar if there is a 0-cycle whose three edges are not contained in S.

By an argument similar to the proof (for BF(2, 3)) of Theorem 2, it can be proved that the 5-spanner T2,4, which

0

Lemma 7. Every cycle of length seven in BF(k, r ) is a 0-cycle, where r 2 6.

0

Lemma 8. Suppose S is a minimum t-spanner of a bipartite graph G, where t is odd. Then S is also a minimum (t +

1)-spanner of G.

Proof: Suppose S' is a minimum (t

+

1)-spanner of G. S' is also a t-spanner of G, for otherwise there exist two adjacent vertices in G whose distance is t

+

1 in S', which implies a cycle of odd length in G. This is a contradiction. Since S is a (t

+

1)-spanner of G, the size of S is greater than or equal to the size of S'. On the other hand, since S is a minimum t-spanner of G, the size of S is smaller than or = (<O, OOO>, <1, loo>) and (ut, ~ 2 ) = (CO, loo>, <1,000>).

011>, 4 , l l P ) , (<O, 111>, (1, 011>), ( 4 , 101>, <2,

contains 80 edges, is minimum.

equal to the size of S'. Hence, the size of S is equal to the

size of S'. U

Theorem 4. A minimum 6-spanner of BF(k, r), which contains (2k

-

1)rkr' edges, can be constructed, where k 2 3 and r 2 6 or k = 2 and r 2 8. A minimum 6-spanner of BF(2, 4), which contains 80 edges, can be constructed. A minimum 6-spanner of BF(2, 5), which contains 208 edges, can be constructed.

Prooj By the aid of Observation 1, Lemma 1, Lemma 3, Lemma 4, and Lemma 6, it can be proved that Sk,r is a minimum 6-spanner of BF(k, r) for k 2 3 and r 2 6 or k = 2 and r 2 8. The proof is similar to the proof (for k 2 3 and r

2 4 or k = 2 and r 2 6) of Theorem 2. Since BF(2, 4) is bipartite, by Theorem 3 and Lemma 8 a minimum 6-spanner of BF(2, 4) contains 80 edges. The 5-spanner T2,4 is a minimum 6-spanner of BF(2,4).

By an argument similar to the proof (for BF(2, 3)) of Theorem 2, it can be proved that the 6-spanner T2,5 which

0

Theorem 1, Theorem 2, Theorem 3, and Theorem 4 can be combined as follows.

Theorem 5. A minimum t-spanner of BF(k, r) for 3 I t I 6, which contains (2k

-

1 ) r T ' edges, can be constructed, where

k

= 2 and r 2 t

+

2 or k 2 3 and r 2 t. A minimum t-spanner of BF(2, r) for 4 1 t I 6, which contains ((2r

-

1)k - r ) r ' edges, can be constructed, where r = t - 2 or t

-

1.

A minimum 7-spanner of BF(2, r) that contains 5r2'2 edges was constructed in [3], where r 2 9. Since BF(2, r) with even r is bipartite, a minimum 8-spanner of BF(2, r) that contains 5r2'2 edges can be constructed according to Lemma 8, where r 2 10 is even. We show in Table I the current status of the minimum t-spanners for BF(k, r). As shown in Table I, minimum t-spanners of BF(2,3) for t I 5 have been obtained. A minimum 3-spanner of BF(2, 3) contains 32 edges. A minimum 4-spanner and a minimum 5-spanner of BF(2, 3) contain 28 edges. Minimum t-spanners of BF(2,3) for t > 5 were not obtained yet.

References

contains 208 edges, is minimum.

L. Cai and M. Keil, "Spanners in graphs of bounded degree," Networks, vol. 24, pp. 233-249, 1994. R. Harbane and C. Padro, "Spanners of de Bruijn and Kautz graphs,'' Information Processing Letters, M. C . Heydemann, J. G . Peters, and D. Sotteau, "Spanners of hypercube-derived networks," SIAM Journal on Discrete Mathematics, vol. 9, no. 1, pp. F. T. Leighton, Introduction to Parallel Algorithms and Architecture: Arrays. Trees. Hypercubes, Morgan Kauhan, San Mateo, CA, 1992.

M. S . Madanlal, G. Venkatesan, and C. P. Rangan, "Tree 3-spanners on interval, permutation and vol. 62, pp. 231-236, 1997.

37-54, 1996.

regular bipartite graphs," Information Processing Letters, vol. 59, pp. 97-102, 1996.

D. Peleg and J. D. Ullman, "An optimal synchronizer for the hypercube," Proceedings of the 20th ACM Symposium on Theory of Computing, D. Peleg and A. A. Schaffer, "Graph spanners," Journal of Graph Theory, vol. 13, no. 1, pp. 99-1 16,

1989.

1987, pp. 77-85.

Table I. Minimum t-spanners of BF(k, r).

k l r

I

Number of ednes

I

2 2

I

2 3

I

r P ' 2 1 3 1 40 (ref. 131) 2 2

I

2 4

I

r F '

I

3 3 216 2 334 (3r

-

1)2" (ref. [3]) 2 5 3r2" (ref. [2], [3]) 5 , 6 2 7 3r2" (Theorem 3) 3 , 4 unknown 2 5 3 unknown 4 80 (Theorem 4) 2 5 208 (Theorem 4) 2 3 (2k

-

1 ) r r ' (Theorem 3) 697 2 8 (3r

-

1)2"-' (ref. [3]) (2k

-

1)rklCl (Theorem 4) 3,435

I

unknown 2 3 2 6

I

(2k

-

1 ) r r ' (Theorem 4) 1 8 unknown 1 9 5r2" (ref. [31) 2 3 2 3 unknown 1 9 Unknown 2 10 unknown 2 odd 2 10 5r2" even 2 3 2 3 Unknown 2 2 2 3 Unknown

-

5:

-

0 0 5: 0 0

E!

0 0 0 m

.-

_cd E c.’

3

c.’ cd n yr)

s