NONPARAMETRIC BAYES RISK ESTIMATION FOR PATTERN-CLASSIFICATION

IEEETRANSACTIONSONSYSTEMS, MAN, AND CYBERNETICS,VOL. SMC-7,NO. 9, SEPTEMBER 1977

capability upon stimulus predictability," Vis. Res., vol. 6, pp.

707-716, 1966.

[20] P.Morasso,E.Bizzi,andJ. Dichgans,"Adjustmentofsaccade char-acteristics during head movements," Exp. Brain Res., vol. 16, pp.

492-500, 1973.

[21] P.Morasso, G.Sandini,and V.Tagliasco,"Plasticityin theeyehead coordination system,"inAspectsofNeuralPlasticity,Vital-Durand andJeannerod, Eds.,INSERM, vol.43,pp.83-94, 1975.

[22] P. Morasso, "EGOS: A minioperatingsystem for management of experiments in neurophysiology and behavioural sciences," Proc. IFAC-IFIP Workshop on Real-Time Programming, Budapest, pp.

259-263, 1974.

[23] C. Prablanc and M. Jeannerod,"Corrective saccades: Dependence on retinalreafferentsignals," VisionRes.,vol. 15, pp.465-469,1975. [24] D. A.Robinson,"Themechanics of human saccadiceyemovement,"

J. Physiol.,vol. 174, pp.245-264, 1964.

[25] ,"Theoculomotor control system:Areview,"Proc. IEEE, vol. 56, pp. 1032-1048, 1968.

[26] ,"Models of saccadic eyemovementcontrolsystem,"Kibernetik, vol. 14,pp.71-83, 1973.

[27]

L. Stark, G. Vossius, and L. R. Young, "Predictive control ofeye

tracking movements," IEEE Trans. HumanFactors in Electronics, vol.

HFE-3,

pp.

52-57,

1962.

[28]

N.SugieandM.Wakakuwa,"Visualtargettrackingwith activehead

rotation,"IEEE Trans.SystemsScienceandCybernetics,vol.SSC-6,

pp. 103-108,1970.

[29]

N.SugieandG.Melvill-Jones,"Amodel ofeyemovementsinduced

byheadrotation,"IEEE Trans.Systems,Man,andCybernetics,vol.

SMC-1,pp.251-260, 1971.

[30]

N. Sugie,"A model ofpredictivecontrolin visualtargettracking,"

IEEE Trans. Systems, Man, and Cybernetics, vol. SMC-1,pp. 2-7,

1971.

[31]

L. R.Young,"Asampleddata model foreyetrackingmovements,"

Sc.D.thesis,Dept.Aeronautics andAstronautics, MIT,

Cambridge,

1962.

[32]

L.R.Youngand L.Stark, "Variable feedbackexperimentstestinga

sampled data model for eye tracking movements," IEEE Trans.

HumanFactors inElectronics,vol.HFE-4,pp.52-57,1962.

[33]

R.Zaccaria,"BSSP: Biologicalsystemssimulation program,"Tech.

Rep.,Istituto diElettrotecnicaGenova,vol.TR 1/75,1975.

Nonparametric

Bayes

Risk

Estimation

for

Pattern

Classification

ZEN CHEN AND KING-SUN FU. FELLOW, IEEE

Abstract-The performanceofapattern classificationsystemis often evaluated based onthe risk committed by theclassification procedure. The minimum attainable risk is the Bayes risk.Therefore,

the Bayes riskcanbeusedas ameasure oftheintrinsiccomplexityof thesystem,anditalso servesas areferenceoftheoptimality measure ofaclassificationprocedure. There are many practicalsituationsin which the nonparametric methods may have tobe called uponto estimate the Bayes risk. One of thenonparametricmethods is via the

probabilitydensityestimation technique. Theconvergenceproperties ofthisestimationtechniquearestudiedunderfairly general assump-tions. In the computer experiments reported, the estimate of the Bayes risk is takenas thesample meanofthedensityestimateby making use of the leave-one-out method. The probability density estimate used is the oneproposed byLoftsgaardenandQuesenberry.

This estimate is shown to be, in general, superior to the risk associated withaBayes-likedecision rule basedontheerror-counting scheme.This estimate is alsocompared

experimentally

with the risk estimate associated with the nearest neighbor rule.

ManuscriptreceivedDecember 13, 1976; revised March 21, 1977. This workwassupportedby the AirForce Office ofScientific Research under Grant 74-2661.

Z.Chen is with theInstituteofComputerScience,NationalChiao Tung University,Hsin-Chu, Taiwan.

K. S.Fuis withtheSchool ofElectricalEngineering,PurdueUniversity,

WestLafayette, IN47907.

I.

INTRODUCTION

ASSUME thereexistsaclassofconditional

probability

densities F

{f,, f2,

A

ftM

in a

probability

space

{S,B,P},

where S is the

sample

space, B is a

a-algebra

of subsetsof

S,

andP isa

probability

measure onB.Letql 2,

*** jm Ii> 0,

EM

1qi = 1, be the prior probabilities of

occurrenceof theM

pattern

classes. Also let

L(i,j)

betheloss

incurred

by classifying

a

sample

from classi

into

class

j.

A

pattern

classification

procedure

isto

assign

anew

sample

in

the

sample

space

(usually

in the form of measurement

vectors)

tooneof the M

pattern

classes. The

performance

of a

pattern

classification

system

is

properly

evaluated

based

on the risk

(i.e.,

the

expected

value of the loss due to

misclassification)

committed

by

the

classification

procedure.

The

minimum

attainable riskis theBayes risk.

Therefore,

the

Bayes

risk canbe used as ameasure ofthe intrinsic

complexity

of the system, and it also servesas a reference ofan

optimality

measure ofa

procedure.

The

Bayes

riskis a

function

ofapriori

probabilities

and

the

underlying

conditional

probability

densities.

Inthecase

where

{ri}

and

{ffi

areknown

completely,

itis well known

[21] that thefollowingrandomizeddecision ruledB attains the Bayes risk:

1,

0,

Oj(x)

=

Xj,

M if Z

tli

L(i,j).f(x)

i=1 M < min L

qiL(i,k)fi(x)

k;j i=1 M if Z

q1i

L(i,j)J;(x)

i=1 M > min E

qiL(i,k)fi(x)

k:tj i=1 M if

E

qj

L(i,j)f(x) i-Mv = min

I

qiL(i,k)fi(x)

kj i= 1

wherexisthe observablemeasurementofthe new sample X,

and

M

L xj= 1, j=1

oti 0 The Bayes risk RB is given by

M RB- S

r1jEjyB(i,X),

it= M

YBQ,X)

= E

L(i,j)d (X),

j=1

where

YB(i,x)

istherisk associatedwith class i committed

by

thedecision rule dB,

given

that therandom vector X takeson the value x, and El is the expectation taken over S with respect

tofi

EF.

In the real

world,

there is often a lack of the exact

knowledge

of {i} and

{tfi;

instead

only partial

information

is

available.

Forinstance,therearesituations in which

only

the

parametric

forms of theunderlyingdistributions

and/or

a setof

correctly

classified

samples

from the distributionsare known. Based on this

partial

information,

parametric

and

nonparametric

methodshavebeen studied

by

many resear-chers to solve the pattern classification

problem.

Nonpar-ametric

methods are used under the condition that no

parametric

forms of

underlying

distributionsareknown or can be

assumed,

[1]-[11].

In this paper the focus is

placed

on the

nonparametric

Bayes riskestimationviathe

sample

meanofanestimator of

the conditional

Bayes

risk which, in turn, employs the

density

estimation

technique.

Various

asymptotic

proper-tiesof theaboveconditionalrisk estimatorarestudied under

fairly

general assumptions.

The

nonparametric Bayes

risk

estimationis

implemented

with the

given

correctlyclassified

samplesona

digital

computer.Theexperimentalresultsare

thendiscussed.

Il.

NONPARAMETRIC CLASSIFICATION PROCEDURE

WITH DENSITY ESTIMATION

In classifying a new sample into one of the

MI

possible

pattern classes, there are two categories of

nonparametric

classification procedures. On the one hand, there are

procedures which do not involve the use of any form of the

underlying probabilitydensities. Under this category there are

i)

the nearest neighbor

decision

rule

[1], [2],

[4]-[7];

ii)

classification procedures based on statistically equivalent blocks

[3],

[18];

iii)theclassification by linear orpiecewise

lineardiscriminant functions[19]; and others. On the other hand,there areprocedureswhichemploydensityestimation techniques [8]-[10]. These procedures are conceptually simple and are analogous to those parametric

methods

in

statistical decisiontheory. Tofacilitatelaterdiscussion,one

ofthe general forms ofthese procedures is given here. Assume that thedensity functions E F, i = 1, 2,

M,

areestimatedfrom thetrainingsample sets by making use of some density estimation technique. Let ,,,(x) denote the

estimate

offi(x),

i

1,

2, ,Mfromaset oftraining samples

{jyY),

, f

()},

i- 1,

2,

, M. Let

XA,

A

{X(l'

,I'(,1,

x()

...',

X(M)} - {X1, X2, , X,

tl

t +

n11

E,and

let j-

ni

n, i -

1,

2,

, M. Based on these estimates, a decision rule, denoted by d°(x), which is directed by the

Bayes rule, is defined as follows:

i 1,

I,

(x)

= 0 aXi, M if ,)j

L(i,j)

fi

n,(X)

i=t

M

<mmin

E

tL(i,k)fjni(x)

k4tj

i=1 if E i

L(i,j)fJ,n,(x)

> min E

tj

L(i,k)fi.n,(X)

k tj i=I if 5

r1L(ij)finj(x)

mmin

5

rjL(i,k)fJ,ni(x)

kj:j i I

(2)

where j >0,j= 1,2, ,M, and

j'

1 1.

III.

ESTIMATION OF

BAYES

RISK

Once the

classification

procedure

isdevised, the

perfor-mance is

mainly

evaluated

by

the misclassification

com-mitted by the

procedure. In

certaincases theestimation of

misclassification

can be related to the

Bayes

risk and is therefore usedtoestimatethelatter. Itwasshown

[4]

that in

atwo-classproblem,theriskofthe 1-nearest

neighbor

rule

Rwith the

(0,1)-loss

functionisrelatedtothe

Bayes

risk R*

by R* <R < 2R*(1

-R*).

Let

Sn/n

be an estimate ofR,

then the interval

[(1

1-

2Sn/n)

2,

S,1n]

isanestimate

of R*.

Therisk

associated

with thedecision rule

do

given

by

(2)

usingthe

error-counting

schemewas indicated toconverge

CHENANDFU: BAYES RISKESTIMATION

Adifferent estimation of theBayesriskcanbe builtupon anestimatorof theconditional

Bayes

risk. The conditional

Bayes risk YB(X)

corresponding

to

(1)

is

given

by

M

YB(X) =

min

L(i,j)pi(x)}

je{, .,

M}b

i=

Pj(x) = nj

fj(x)l/

E qi

fi(x))

Now define

pj,n(X

Xn)

=

{ij fj,nJ}E

(j

'ini(X)

i and

y~n(X

Xn)

= min

jcti

1ml**

..IM} M E L(inj)pi,n(X Xn)|* =1

Notice that

fpj,n(x

Xn)

and

yn0(x

Xn)

areconditionedon

Xn

and,

therefore,

are random variables.

Itwillbeshown that

y0(x

Xj)

isaconsistent estimatorof

YB(X). Consequently,

RB

canbeinferred

by

anestimatorof

Exy7n(X Xn)

IV. ASYMPTOTIC PROPERTIESOFy°(X

Xn)

Before theasymptotic

properties

of

-yn°(X

Xn)

are

studied,

someassumptionsandnotations will be

introduced

first.In

the

following

it will beassumedthat theconditional

probab-ility densitiesf1, i = 1,2,

...,

M, are

absolutely

continuous

and bounded from

above,

and that their estimates

fn,(x),

i= 1, 2, , M, are

nonnegative.

In

addition,

assume

J,ni(x)

P4f(x),

i =

1, 2,

,

M;

namely,fn(x)

converges to

f(x)in

probability

fori = 1,2, ,M.Also assumethat the loss functions

L(i,j),

i, j = 1,2, ,M,arenonnegative and

finite. Let thenotation

ni

-+ oo indicate

ni

-*oo,for i=

1, 2,

* M.

Besides,

EX

y°(x

Xn)

meansthe

expectation

is taken withrespect toallX1,X2,. ,

Xn.

Analogous

interpretations

apply to

ExyT(X

IXn)

and

Ex7EX/n(X

IXn).

Finally

define

Rn

=

Exj{ExnY(X

Xn)}-Xn

|Y(x

Xn)

[E

1ifi(x)

dx}.

Lemma 1:

i)'no(XI|Xn) P B(X)

and

ii) lim

E.y

(x|Xf)=yB(x).

nio

Proof:Since ,j-- t,i= 1,2, ,M,almosteverywhere

(a.e.) by the law oflarge numbers [17], this, together with

f,i(x)A

fi(x),

i- 1, 2, M, implies p Xn)-px),

j= 1, 2, M, and, therefore, y7n(x Xn) YB(X).

Furthermore,

forevery n

(kn),

with probability

1,

1yn

(X

Xn)

=

Em

L(i,j)Pi,n(X

Xn)

je1, M} i=1

< min

LE

E (x

Xn)j

=L < oo

where L is themaximum value of

L(i,j),

i,

j

= 1, , M.

By

Lebesgue's

dominated convergence theorem,

lim

Ex4?n

(X

Xn)

=

YB(X)

ni-o0

Vxexceptforasetof

points

withzeroprobabilitymeasure.

Theorem 1: R°

converges

to

the Bayes risk

RB

in the

ordinary

sense, as ni-* cx.

Proof:

Since

Ex,

y0(x

Xn)

<

L

almosteverywhereand

Vn

by

Lebesque's

dominated convergence

theorem,

lim R° = lim

ExExy

(X

IXn)

ni-+cc ni-0o

-Ex lim E.yn(X Xn) = EXVB(x)= RB. Theorem 2:

y°(x

|

Xn)

-*E'+y°(x

E X4

Proof:

Iyot(xI

Xn)

Exn

y(X Xn)I

=

yo(x

Xn)

- lim

Exnyo(x

Xn)

)

(x

E7

n)

ni-oo

+ lim

EXyYno(x|

Xn)

<

yo°(x

Xn)

- lim

EXnYno

(X |Xn)

nin-0

+

jEx/yn(xXn)-

lim

Ex

yV(IX|)I.

ni-oc

Given

£ >0 we can find

i1

>0 and 82>0 such that 8= + 82.

By

Lemma

1,

lim Pr

{yo(xIXn)-

lim E

.2}1=

ni-oo ni-c°

andthereexistsmi,i= 1,

2,

,M,if

ni

mi, i=

1, 2,

*,M,

Ey0

yn(x

Xn)- lim

Ex"7no(x

Xn)|l< cx

lim

Pr {

yn°

(xj|

Xn)-Exn

yn°

(x|Xn

)X

X.

8}

<

fl1-i

li>r70(

0i

Xim

Pr El°

_x,

0n)-Xlm

E;,n°xln)

)

ni nio

+

IEPrA

°(x

IXn)-

lim

Ex

.7n(X

)I

.n<8}

ni-oo

> lim Pr

{y10(xIXn)-

lim

E

nyn(xfXn)j

.8-81}

ni-o ni-+o

= 1

i.e., 7n

(X

Xn)

E+E

n°(X

Xn)-Corollary

1:

y0(IXn)

Ex2(xIXE)

in the

kth mean

(k

>

0).

n

Proof:

Since

In(x

Xn)

<L< oo, a.e.,Vn, the conver-gencein

probability implies

theconvergence in the kth mean

[17]. Therefore,

Corollary 1 follows fromTheorem 2.

Theorem 3:

Ex7

y(X

Xn)

P EX{EXny2(X

Xn)}

Proof: For any E >0, by the Markov inequality

[17],

lim Pr {

ExTy(X

Xn)-Ex(Ex70(X

Xn)) 2

ni- oo

K lim

{Ex, EX7J(X

Xn)

-

EX(Exy

y (X

Xn)

ni-oo

(im

|Ex,

({c

l°(x

I

Xn)-

Ex,Y(x

I

X)Idx)

8

where c isa constant such that M

f(x)=

E

fi(x)<c

it=1

forevery x except for a set ofpoints withzero

probability

measure, since

Ex7y(X

Xn)-

ExExnyn(X

Xn)

. Ex

jy0(X

Xn)

-

Ex,yO(X

Xn)

= F

7(x

Xn)

-

Ex

7y5(xI

|

f(x)

dx

. {

cIy,¶'(xlXn)-Exyn°(xIXn)I

dx.

Now

Ex,, y°(x

I

Xn)-EE.

70(x

I Xn) <c' < so, a.e., Vn, by

Corollary 1,

lim

Exj yo(x

I

Xn)-Ex,,y°(x

I Xn)

0.

Mni-oo

By

Lebesgues's

dominated convergence

theorem,

lim Pr

_n,r~~~

{

Exyo(X Xn)

-

Ex(EX")

Y(X Xn))

. £ ni- cc

<c

<c(J ur

JXlim E,,

~n

yn°(x Xn)

n

-Ex.7°(x

Xn)

dx /8-O

8=

i.e.,

ExaT(X

Xn)-

Ex{Exnyo(X

Xn)}

Corollary

2:

Exy°(X

X1)

Ex{Ex,

7y(X

Xn)}

in the kth

mean.

Theorem 4:

Ex

TO(X

I

Xn)

RB.

Proof: From

above,

RB

= lim

Ex,xnyo(X

Xn)

and

Exy°(X

Xn)

4

ExtExnyno(X

Xn)}

By a

technique

similar to the one used in the

proof

of

Theorem 2, itcan be shown that

Since

Ex,y(XI

Xj)

<L < oo, a.e.,

val,

the following

corollary can be shown.

Corollary 3:

Ex-o(X

X)-*RB in the kth mean. In particular,

<

Ex(Exy(X

Xn))

-RB

<

EyXE,,

Ex'(X

Xj)-RBI

O

0

as ni

XC

and

ExnIEx

y(XIXn)-

R12

-0 as ii- oo Vi.

The previoustheorems and corollaries are the foundation

for

yT(X

Xn)

to be used in the Bayes risk estimation. The

expectation of

y°(X

Xn)

is shown to converge to the Bayes

riskinprobability as well as in the kth mean, in contrast to the convergence of the risk of the nearest neighbor rule

which is only to a bound on the Bayes risk. This result indicates the use of a sample mean of

j!°(X

Xn)

as a desirable estimation of the Bayes risk. The empirical comparison of

this estimator withtheotherestimators will be given in the nextsection.

V. UTILIZATION OF GIVEN SAMPLES IN ESTIMATION

In order to estimate the risk by using the correctly classified samples, two things must be decided. One is to

choose a probability densityestimation technique and the

other is to decide on a method to effectively utilize the

available labeled samples to carry out the estimation scheme. Asfarasthefirstproblem is concerned,thedensity estimator proposed originally byParzen

[13]

and extended later byCacoullos

[14],

the oneby Murthy

[15],

and theone

by Loftsgaarden and Quesenberry

[12]

allmeetthe

consist-ency requirement ofthe

density

estimation. Itis the latter one which was

employed

in the computer

experiments

reported.

In

utilizing given

labeled

samples

to carry out the risk

estimation,

thereare

mainly

three methods.

They

are

i)

the

resubstitution method;

ii)

the holdout

method,

or H

method; and

iii)

the leave-one-out

method,

orthe Umethod

[16].

Generally

speaking,

the first method

gives

an

overly

optimistic

estimate,

whilethesecondmethod

gives

an

overly

pessimistic

estimate. The third method

yields

an estimate

with a small amount of bias

compared

with those of the

previous two

methods,

although

it suffers from

requiring

more computation time. It is the third method which was

used in the computer

experiments.

The

application

of the leave-one-out method to the

estimation oftheBayesriskdiscussed

previously

leadstoan estimator

A°(Xj)

which is

given by

M

,k°(Xn)

=

lln

>; I°l(Xi X1, *.* I Xi-11 Xi+1~'*'' Xn).

it-Theuseof

R°(Xn)

in

estimating

the

Bayes

risk is

justified

bythe

following

convergence theorem.

Theorem 5:

R°(X11)

converges to the

Bayes

risk

RB

in

probability as well as.in the kth mean

(k

>

0).

From Lemma 1, itcan be shown that 0n l(Xil Xi_1 Xi+li ' ' Xn)

A nO

(xl ATn1

0).A

655

CHEN AND FU:BAYES RISKESTIMATION

By the Markovinequality,

n n

Pr _{< n£)1}

_XiJXn

1)- 1(~

- (

X)B(Xi)

i=l i=1

By the convergence theorem in the kth mean [17],

n n

<1/n

E

Yn°_AXijXn-

1)/_

E

YB(Xi).

i=n1 i=1

Because the Xi are i.i.d., the

yB(X-)

are also i.i.d. By

Bernoulli's law, (1/n) E

YB(Xi)

-

EXYB(X)

= RB. i=1 Thus n

(1/n)

E

y0_j(XijXn_j-+RB

i=1

in

probability

aswellas inthe kth mean.

An

interesting

remark is in order.

Experimental

results

indicate that

R2(Xn)

has a smallervariance than does the

Bayes risk estimate

by

the risk associated with the

classification

procedure

obtained from theerror

counting

method. The reason may lie in the fact that

R&(Xn)

is a

smoother function

compared

with the error

counting

risk

estimate.

Therefore,

R°(Xo)

convergestothe

Bayes

riskmore

rapidly.

VI. COMPUTER EXPERIMENTS

The estimation of the

Bayes

risk discussed above is implemented on a

digital

computer. In the

following,

the

constant

{kn}

is referred to as the sequence of

positive

integers of the

Loftsgaarden

and

Quesenberry estimator

of

the density estimation. Let

R°,

RE, and Rk be the estimators of the Bayes risk

by

threedifferent

models, namely,

those basedonEx

y°(X

Xn),

the riskassociated with thedecision rule

d°(x),

andthek-NN decision

rule,

respectively.

Thedata

used in the

experiments

are bivariate Gaussian data

N(yi,i)

i =

1,2,

where

3.08

-

3.0\

81 =

\1.0}

I2 -

.0)

and

E m = (20

02)

Experiment

1: Five sets ofsampleswere generated with = n2 = n = 100, 150, 200.

R°

is obtained by the

leave-one-out method and the holdout method. The holdout

sample sizescorrespondingto n = 100, 150, and 200 are 25,

50,and75,respectively.The results areshownin Table

I.

As the results indicate, the U method is better than the H method.

TABLE I

AVERAGEANDSTANDARDDEVIATIONFOR R°WITHkn=(n)0.55 n n U Method H Method Avg. SD Avg. 1 SD 100 150 200 0.1363 0.1275 0 . 1 248 0.0259 0.0067 0.0067 0. 1472 0. 1406 0.1357 0.0461 0.0357 0. 0271 TABLE II

AVERAGEANDSTANDARD DEVIATIONFOR R°ANDREWITHn1 =n= 150,kn Rn(U Method) RE ' Avg. SD Avg. SD 0.45 0.1168 0.011J 0.0760 0.0134 0.50 0.1242 0.0113 0.0733 0.0139 0.55 0.1275 0.0067 0.0700 0.0139 TABLE III

AVERAGEANDSTANDARD DEVIATIONFOR

R°RE,ANDR3WITHkn=(n)

.10~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Rn(U Method) RE R3

1l=n2

Avg. SD Avg. SD Avg. SD

50 0.1562 0.0126 0.060 0.0316

75 0.1320 0.0152 0.0653 0.0152 0.0627 0.2433 100 0.1363 0.0259 0.064 0.0297 0.079 0.0222 150 0.1275 0.0067 0.070 0.0139 0.0733 0.0238 200 0.1248 0.0067 0.066 0.0133 0.077 0.0124

Experiment 2: Fivesets of sampleswere

generated

with

n,

=n2 =n 150. R°is obtainedfor threedifferent values of kn

i.e.,

kn =na, i=1,2,3, with

aI

=0.45, a2=0.5, and

O3=

0.55. The results are summarized in Table II. R° is much closer to the truerisk

(RB=

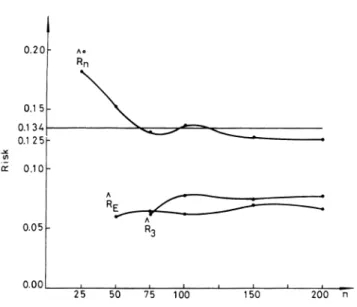
0.134)thanRE. For the

sample sizes under consideration, R° issuperiorto RE. Experiment3:Forn1 =n2= 25,50, 75,100,150,200,five

setsoftraining samplesweregenerated.Thethree Bayesrisk estimates

R0',

RE, and R3are computed. The experimental

resultsareshown inTable III andFig. 1. We can find thatR° isbetter than REandR3.BothREandR3areoptimistic risk

estimates.

It is important to know that the ability of

R°(Xn)

in

estimating the Bayes risk well relys on the appropriate

choice of theconstant

kn.

Animproper choice may lead to poor results

[20].

VII. CONCLUSIONS

Inthis paper focusisplaced onthe nonparametric Bayes riskestimation.Theestimate based on the conditional Bayes

risk estimator is employed by making use of the density

estimation. Various asymptotic properties of this estimate

0.20t A* Rn 0.15k 0.125 0.12 5 0.10F 0.05p- R3 2 5 50 75 100

Fig. 1. Plot of Bayes risk estimates versus

class).

The computer implementation ofth

riskwith thegiven samplesbytheleave

given. Theestimateconverges totheBa

lityandinthekthmean. Itwasshownti

basedontheconditional Bayesriskisg

the riskestimateassociated withaBay(

d°.

FortheGaussiandataused,R°5 wass

the BayesriskthanREandRkwere.Ho

of constants in the estimate may

to deteriorate.

The Bayesriskestimationdiscussed

priori information of the pattern unde

Thispoint lends themethod to a numl

1) TheFeature Selection Problem:C

tern classification problem there are

selectingan effective set of features. A

select aset of featurewhichyields thes

estimated Bayes risk. The set of feat

generally will lead to an efficient classi

2) The Measure ofSeparability of I

analysisthemeasureofseparabilityoft

by means of the Bayes risk estimatioi

insight into thestructure ofclusters.

REFERENCES

[1] E. FixandJ. L. Hodges,Jr.,"Discriminatoryanalysis,nonparametric

discrimination," USAF School of Aviation Medicine, Randolph

Field, TX, Project 21-49-004, Rep. 4, Contract AF41 (128)-31* Feb.

1951.

[2] ',"Discriminatory analysis: Small sampleperformance,' USAF

School of Aviation Medicine, Randolph Field, TX,Project21-49-004, Rep.11,Aug. 1952.

[3] T. W. Anderson, "Some nonparametric multivariate procedures

based on statistically equivalent blocks," inMultivariateAnalvsis, P. R. Krishnaiah,Ed. New York: Academic Press, 1966, pp. 5--27.

[4] T. M.Coverand P. Hart,"Nearest neighbor patternclassification,"

.____________

IEEE Trans. Inform. Theory,vol. IT-13, pp. 21-27, Jan. 1967.

[5] D.W. Paterson,"Someconvergence propertiesofanearestneighbor

decision rule," IEEE Trans. Inform. Theory, vol. IT- 16. pp. 26--31,

Jan. 1970.

[6] T. J. Wagner, "Convergence of the nearest neighbor rule," IEEE Trans. Inform. Theory, vol. IT-17, pp. 566-571, Sept. 1971.

[7] D. L. Wilson, "Asymptotic properties ofnearestneighbor ruleusing 150 200 n editeddata,"IEEETrans.Syst.Sci.Cvbern., vol.SSC-2,pp.408-421,

July 1972.

(number of samples per [8] J. Van Ryzin, "Bayes risk consistency of classification procedures using density estimation," Sankhya, Ser. A,pt. 2-3, vol. 28, pp.

261-270, Sept. 1966.

[9] S. C. Fralick and R. W. Scott, "Nonparametric Bayes risk estima-tion," IEEETrans.Inform. Theory,vol. IT- 17,pp.440-444,July1971.

e estimate ofBayes [10]E. A.Patric and F. P. Fischer,II,"Introductiontotheperformanceof

distribution free, minimum conditional risk learning systems,"

-one-outmethodis School of Electrical Engineering, Purdue Univ.,Lafayette, IN,Tech. Lyesrisk in probabi- Rep. EE67-12,July 1967.

hattheriskestimate

~at

[11]

T. Cover,

"Learning

in pattern

recognition,"

in Methodologies of

the riskestimate

Pattern

Recognition,

S.

Watanabe,

Ed.

New York:

Academic Press,

;enerally

superiorto 1969,pp.111-132.

es-likedecision rule

[12]

D. 0. Loftsgaarden andC. D. Quesenberry, "A nonparametric

esti-~hown

tobecloserto

mate

of

a

multivariate

density

function,"

Ann.

Math.

Stati.st..,

vol. 36,

pp. 1049-1051,1965.

wever, abadchoice [13] E. Parzen,"On theestimation ofaprobability densityfunction and

cause the results themode,"Ann.Math. Statist., vol. 33, pp. 1065-1076, 1962. [14] T. Cacoullos, "Estimation of a multivariate density," Alin. Matlh.

Statist.,vol. 18,pp. 179-189, 1966.

aboverequires no a [15] V. Murthy, "Estimation of probability density," Annti. Math. Statist.,

Nrlying

distribution. vol. 36,pp. 1027-1031, 1965.

ber of applications.

[16] P. A.

Lachenbruch

and M.

R.

Mickey,

"Estimation

of

error rates

in

discriminant analysis," Technometrics, vol. 10, pp. 715---725, Feb.

2uite often in a pat- 1968.

no clear rules for

[17]

M. Loeve, Probability Theory, third ed. Princeton, NJ: Van

Nos-trand, 1963.

good practice isto [18] G. W. Beakley and F. B. Tuteur, "Distribution-free pattern

;mallestvalue of the verification using statistically equivalent blocks," IEEE Tran.s. ures thus obtained Comput., vol.C-21,pp. 1337-1347, Dec. 1973.

fier

design.

[19]

K. Fukunaga, Introduction to Statistical Pattern

Recognitionl.

New

York:Academic Press, 1972.

Clusters: In cluster [20] Z.Chen,"Nonparametric methods for nonsupervised andsupervised

heresultantclusters patternrecognition," Ph.D.dissertation, Purdue Univ.,West

Lafay-provide good ette,IN, 1973.

canprov ide good [21] T. S. Ferguson, Mathematical Statistics: A Decision Theoretic

Approach. New York:Academic Press, 1967.

U.VVI ---- I