On the Least-Squares Monte Carlo (LSM) for Pricing American Barrier Options

On the Least-Squares Monte Carlo

(LSM)

for Pricing American Barrier Options

Chia-Peng Lee

Department of Finance

National Taiwan University

Contents

1 Introduction

2 The Decomposition Technique for American Options

2.1 Valuing American Puts

2.2 Valuing American Barrier Put Options

3 The LSM Methodology

3.1 The Valuation Framework

3.2 Valuing American Puts

3.3 Valuing American Barrier Put Options

3.3.1

The Homogeneous Property of American

Barrier Options

4 Conclusion

Bibliography

Abstract

Barrier options are options that are either extinguished (“out”) or established (“in”), when the price of the underlying asset crosses a particular level (“barrier”). Common examples are “down-and-out,” “down-and-in,” “up-and-out” and “up-and-in” options, which can be calls or puts. An additional feature of some barrier options is that a rebate is paid when the option is extinguished or an additional premium is due when the option is established. Closed-form formulas for European barrier options are known in the literature. This is not the case for American barrier options, for which no closed-form formulas have been published. One has therefore had to resort to numerical methods. Using lattice models on binomial or trinomial trees for the valuation of barrier options is known to converge extremely slowly compared to plain vanilla options. In this thesis we show how to apply a simple, yet powerful, least-square Monte Carlo algorithm to approximate the value of American barrier options.

Chapter 1

Introduction

There has been an explosive growth of financial derivatives markets during the last decades. The broad types of derivatives include equity, commodity, foreign exchange, and credit. Of particular interest are American options, which can be exercised at any time between the start of the contract and its maturity. The valuation of options with early-exercise features remains a difficult problem in many important settings, particularly for multifactor models. The major difficulty in handling the early-exercise features comes from the need to estimate the optimal exercise boundary. In contrast to the availability of closed-form solutions for European options, American options typically do not enjoy such formulas. Then we need numerical methods to overcome this pricing problem.

The paper by Longstaff and Schwartz (2001) presents a simple yet powerful new approach for approximating the values of American options via simulation. Their least-squares Monte Carlo (LSM) algorithm estimates the price of an American option by stepping backward in time. At any exercise time, the holder of an American option optimally compares the payoff from immediate exercise with the expected payoff from continuation (i.e., not exercising it). The key to

this approach is that this conditional expectation can be estimated from the cross-sectional information in the simulation by using regression. The fitted value from this regression provides a direct estimate of the conditional expectation for each exercise time. By estimating this conditional expectation function for in-the-money paths and comparing it with the value for immediate exercise, the optimal exercise strategy along each path can be estimated well. Discounting back and averaging these values for all paths results in the present value of the option.

Options whose payoff depends on whether asset’s price attains or fails to a given upper or lower level are called barrier options. Such contracts have become the most popular of exotic options. The main reason for their popularity is that although standard put or call options are useful risk management tools, they may not be suitable for hedging certain types of risks. For instance, the holder of a barrier option acquires option coverage on only a subset of risky outcomes for which a plain vanilla option pays off; this reduces the cost of the resulting coverage so that the barrier-option holder does not have to pay for the contingencies the holder thinks are unlikely to occur. Because of this flexibility, barrier options are widely used in currency markets (see Banks (1994) [1]). In addition, American barrier options offer the added flexibility of early exercise. No closed form solution for American barrier options exists in the literature. The techniques used to value American barrier options have therefore been numerically oriented. Lattice methods have been especially popular. Standard lattice methods have been shown to convergence extremely slowly. Boyle and Lau (1994) and Ritchken (1995) develop a restricted binomial/trinomial method to overcome the problem. However, with these methods, it is still extremely

the underlying asset. Cheuk and Vorst (1996) develop a time-dependent shift for the trinomial tree, and Figlewski and Gao (1999) introduce an adaptive mesh model that grafts high-resolution lattices around points that cause the inaccuracies in the binomial tree. Gao, Huang, and Subrahmanyam (2000) use the decomposition technique to the valuation of American barrier options. In this thesis, we propose a least-squares Monte Carlo simulation to the valuation of American barrier options. This approach is easy to implement since nothing more than least squares is required. We use this technique to value the American barrier option.

This work is organized as follows. We first briefly describe and apply the decomposition technique in the next Chapter. The LSM methodolody is covered in Chapter 3. Concluding remarks are given in Chapter 4.

Chapter 2

The Decomposition Technique for American

Options

In this chapter, we first obtain an analytic representation for American options

using the decomposition technique. Before proceeding with the analysis, we first define our notations as follows:

P_E: the price of a vanilla European put option P_A: the price of a vanilla American put option

P_E-uo: the price of European up- and- out barrier put options

A-uo

P : the price of American up- and- out barrier put options the early exercise boundary of American put options

rrier put options :

P

2.1 Valuing American Puts

Under the usual assumption of constant risk-free rate r, volatility σ, and a lognormal process for the underlying asset, and no dividend payment, Carr,

t

B :

uo-t

B : the early exercise boundary of American up-and-out ba

P the premium of American put options

rt

A E

d S B t

P S K

=

P S K

+

∫

rKe N

−

−

dt

where N(．) represents the cumulative standard normal function and

Jarrow, and Myneni (1992), Jacka (1991), and Kim (1990) obtain the following formula for the price of an American put:

T

[

2 0

]

0 0 ₀

( , , )

( , )

( , )

_t

(1)

(

)

(

)

(

)

2 lo g (x /y)+ (r+ σ /2 )t 1 2 1 d x , y , t = σ t d x , y , t = d x , y , t -σ t

The early exercise boundary B = B : t < 0,T_t

{

_t

[ ]

}

is determined by the

(2)

Once is obtained, the price of the American put can be calculated easily. us

following integral equation:

[

]

- ( - ) 2

- ( , , - )

-

( , )

T r s t _s t E t _t

d B B s t

t

K B P B K

=

+

∫

rKe

N

ds

t B Ju

(1998) es the multi-piece exponential (MPE) method to handle this problem. Under this scheme, multiple exponential functions are used to approximate the exercise boundary, each of which is defined by two variables which are in turn determined by continuity and smoothing-pasting conditions. Assume

bt t

B =Be for the interval

[

t ,t_{1 2}

]

, where parameters B and b are to be d later. Under this s e, the premium become

(

determine chem s

P S K B b t t

t1

, , , , ,

1 2

)

≈

K I S B b t t

×

(

t1

, , , ,

1 2

)

(3)

Integration by parts then yields

(

)

(

)

(

) (

)

(

) (

)

2 0 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 2 1, 2 ₁ 1 2 1 1 2 2 ( ) 2 2 1 1 ( ) 2 2 1 1 ( , , )

1

(

1)

2

1

(

1)

2

( , , ,

)

-

(

t _{rt bt} t rt rt y z x y z x d S Be t

x

e

z

x

e

z

I S B b t t

re N

d t

e N xt

yt

e N xt

yt

N zt

yt

N zt

yt

N zt

yt

N zt

yt

− − − − − − − − − − − + −

⎡

⎤

=

_⎣

_⎦

=

+

−

+

⎡

⎤

+

+

_⎣

+

−

+

_⎦

⎡

⎤

+

−

_⎣

−

−

_⎦

∫

4)

with _{x= (r b σ /2)− − −} 2 , _{y= ln S/B /σ−}

( )

_{andz= x +2r .} 2

If we define P1, P2, P3, as the approximate option values corresponding to

approximating the early exercise boundary as a one-piece exponential function

( 11t

11

B e ) , a two-piece exponential function ( , ), and a three-piece

exponential function ( , ), respectively, then the Ps are

given by 22t 22 B e 21t 21 B e 31t 31 B e 32t 32 B e , 31t 31 B e

11 11 11 1 11

( ,

,

, 0 , )

if

if

(5)

E

P K I S B

b

T

S

B

P

K S

S

B

+ ×

>

⎧⎪

= ⎨

−

≤

⎪⎩

22 22 22 21 21 22 2

( ,

, , 0, )

( ,

, , , ) if

2

2

if

(6)

E

T

T

P K I S B b

K I S B b

T

S B

K S

S B

P

⎧ + ×

+ ×

>

⎪

⎪

=⎨

−

≤

⎪

⎪⎩

33 33 32 32 3 31 31 33

( ,

,

, 0 , )

( ,

,

,

, )

2

2

( ,

,

,

, )

if

2

if

(7)

E

T

T

P K I S B

b

K I S B

b

T

T

P

K I S B

b

T

S B

K S

S B

⎧ + ×

+ ×

⎪

⎪

⎪

=

_⎨

+ ×

>

⎪

⎪

−

≤

⎪⎩

33

To determine B’s and b’s, we apply “an iterative root-finding algorithm”. For example, to determinate B₂₂ and b , applying an iterative root-finding ₂₂ algorithm at t＝0 yields 1 22 22 22 22 22 22 21 21 22 22 22 22 22 21 21

( , , )

( , , ,0, /2)

( , , , /2, )

(8

1

( ( , , ))

( , , ,0, /2)

( , , , /2, ) (9)

E S S S S

K B P B KT K I B B b

T

K I B B b T T

N d B KT K I B B b

T

K I B B b T T

− =

+ ×

+ ×

− =−

+ ×

+ ×

)

(

)

The function Is (…) is defined by

(

)

(

)

(

)

(

)

(

)

(

)

1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 1 2 1 2 1 1 2 2 ( ) 2 2 1 1 ( ) 2 2 1 1 ( ) 2 1 ( 1) 2 1 ( 1) 2 1 ( 1) 2 , , , , 1 ( ) ( )

{

S rt rt y z x y z x y z x x e z x e z x e z I I S B b t t S e N xt yt e N xt yt S z x N zt yt N zt yt z x N zt yt N zt yt n zt σ − − − − − − − − − − + − + + ∂ = ∂ = − + − + ⎡ ⎤ + − _⎣ + − + _⎦ ⎡ ⎤ − − + _⎣ − − − _⎦ +

(

)

(

)

(

)

(

)

2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 1/ 2 2 ₂ 1 1 ₁ 1/ 2 1/ 2 ( ) 2 2 ₂ 1 1 ₁ 1 ( 1) 2

} (10)

y z x x e z yt t n zt yt t n zt yt t n zt yt t − − − − − − − − − + ⎡ _{+ − +} ⎤ ⎣ ⎦ ⎡ ⎤ − − _⎣ − − − _⎦ y= ln S/B /σ−

( )

, and_{z= x +2r .} 2

The B’s and b’s can be obtained by the two-dimensional Newton-Raphson method [12]. To find B₁₁ and b , the approximations of MacMillan (1986) ₁₁ and Barone-Adesi and Whaley (1987) provide a good initial estimate for and zero provides a good initial estimate for

11

B

11

they provide good initial estimates for finding B₂₁and b respectively. To find ₂₁

22

B and b , ₂₁ B₂₁ and b are good initial estimates. ₂₁

In this thesis, we recommend a three-point Richardson scheme to improve convergence. If P1, P2, and P3 are the values given in equations (5), (6), and (7),

then the American put price is approximated by

3 2 1

ˆ 4.5

_A

4

0.5

(10)

P

=

P

−

P

+

P

To illustrate the result, Table 1 reports the values of the early exercise option implied by the binomial tree (time steps equal to 5000) and the decomposition techniques. It is a set of contracts for comparison. The set consists of sixteen contracts that have different values of the underlying asset price St at valuation

date t, the time-to-expiration T, and the volatility parameter σ. The strike value K is fixed at 45. The risk-free rate r is chosen to be 0.0488. In a set, St = (40;

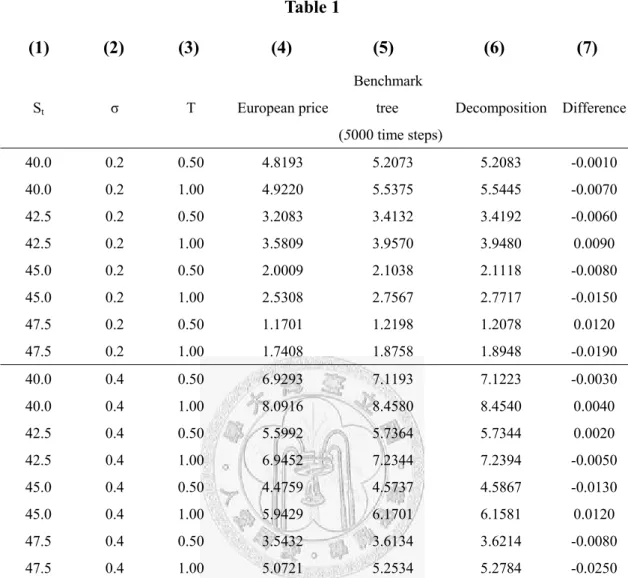
42:5; 45; 47:5), T = (0.5; 1.0), and σ = (0.2; 0.4). As a result, the set of contracts include out-of-the-money, at-the-money, and in-the-money options. The decomposition approximation is based on the observation that the early exercise premium does not depend on the exact values of the early exercise boundary critically. This insight allows us to approximate the early exercise boundary as a multi-piece exponential function. Because the resulting integral of the early exercise premium can be evaluated analytically, an accurate approximation is obtained. Table 1 shows that the approximation based on a three-point extrapolation scheme have the accuracy of a 5000-time-step binomial tree model.

Table 1 (1) (2) (3) (4) (5) (6) (7) St σ T European price Benchmark tree (5000 time steps) Decomposition Difference 40.0 0.2 0.50 4.8193 5.2073 5.2083 -0.0010 40.0 0.2 1.00 4.9220 5.5375 5.5445 -0.0070 42.5 0.2 0.50 3.2083 3.4132 3.4192 -0.0060 42.5 0.2 1.00 3.5809 3.9570 3.9480 0.0090 45.0 0.2 0.50 2.0009 2.1038 2.1118 -0.0080 45.0 0.2 1.00 2.5308 2.7567 2.7717 -0.0150 47.5 0.2 0.50 1.1701 1.2198 1.2078 0.0120 47.5 0.2 1.00 1.7408 1.8758 1.8948 -0.0190 40.0 0.4 0.50 6.9293 7.1193 7.1223 -0.0030 40.0 0.4 1.00 8.0916 8.4580 8.4540 0.0040 42.5 0.4 0.50 5.5992 5.7364 5.7344 0.0020 42.5 0.4 1.00 6.9452 7.2344 7.2394 -0.0050 45.0 0.4 0.50 4.4759 4.5737 4.5867 -0.0130 45.0 0.4 1.00 5.9429 6.1701 6.1581 0.0120 47.5 0.4 0.50 3.5432 3.6134 3.6214 -0.0080 47.5 0.4 1.00 5.0721 5.2534 5.2784 -0.0250 Comparison of the binomial method and the decomposition techniqe’s values for the early exercise option in an American put option on a share of stock. The early exercise value is the difference between the American and European put values. In this comparison, the strike price of the put is 45, the short-term interest rate is 0.0488, and the underlying stock price S, the volatility of returns σ, and the number of years until the final expiration of the option T are as indicated. The European option values are based on the closed-form Black-Scholes formula. Column 5 shows the numerical results of option values form the binomial method with at least 5,000 time steps (the benchmark). Column 6 shows the numerical results from an analytic approximation technique: the 3-step multi-piece exponential (MPE) approximation with Richardson extrapolation.

0 0 ₀ 2 2 2 2 0 0 2 0

( , )

( , )

[ (

( , , )) ( / )

(

(

/ ,

, ))

(11)

T _rt A uo E uo t uo t

P

S K P

S K

r K e

N d S B t

H S

λ

N d H S B

t d t

− − − − −

=

+

−

−

−

∫

2.2 Valuing American Barrier Put Options

In this section, we apply the decomposition technique to other nonstandard American options when the early exercise premium can be represented as integrals involving the cumulative normal function. One particular example is American barrier options. Gao, Huang, and Subrahmanyam (1996) have derived quasi-analytic formulas for American barrier options. The focus of this thesis is on the valuation of “up-and-out” barrier put options using LSM. The price of an American “up-and-out” barrier put option is given by

where

(

)

(

) (

)

2 2

(

2

)

0, 0, / 0 / 0, E u o E E P ₋ S K = P S K + H S λ− P H S K (1 2 ) 2

is the price of an European “up-and-out” barrier option, is the

Black-Scholes formula for standard European put options, H is the barrier, and

E

P

2

(r / 2) /

λ = +σ σ

.

The form of the above formula is very similar to that in

equation (1); therefore the method of approximating the early exercise boundary as a multi-piece exponential function applies.

The early exercise boundary B = B : t < 0,T is determined by the _uo-t

{

_uo-t

[ ]

}

following integral equation:

( ) 2 2 2 2 0 2 0

( , )

[ ( ( , ,

)) ( / )

( ( / ,

, ))]

(13)

T _{r s t} t E t _t t s uo t

K B P B K

rKe

N d B B s t

H S

λ

N d H S B t d s

− − − −

− =

+

−

− −

−

∫

Assume bt uo-t

B =Be for the interval [t1, t2] where parameters B and b are to be determined later. Under this approximation, the premium becomes

(

)

(

)

(

)

2 2

(

2

)

1, , , , ,1 2 1, , , ,1 2 / 1 / , , , ,1 1 2 (14)

uo t t t t

P S K B b t t ≈ ×K I S B b t t − ×K H S λ− ×I H S B b t t

where I is the same as in equation (4)

Suppose the exercise boundary is to be approximated by three pieces of exponential functions. The boundary is then specified by the set of parameters (B, b). Given the boundary, the option price can be determined as follow:

3 1 3 3 1 1 3 3 0 0 2 2 2 3 3 0 0 0 0

( , , )

( , , ,( 1) /3, /3)

( ,0, )

( / )

(

/ , , ,( 1) /3, /3)

(15)

i i i E uo i i A uo i i

P

S K T

K I S B b i T iT

P

S

T

H S

K I H S B b i T iT

K S

λ = = = − − −

⎧

₊

_∑

_×

₋

⎪

⎪

≈ −

⎨

∑

∑

×

−

⎪

−

⎪

⎩

To determine B’s and b’s, each pair of (B, b) has to be determined by simultaneously solving two nonlinear equations:

1 1 1 1 2 2 1 2 1 1 1 , , 1 , , , , 1 , , , , 1 N N i i N i N N i i i i b T b T N _N N _N E uo i i i i N _{b T bj T} N N N N N i j j j i i N _{bj T} N N N j j i i b T b T j i N N N N i i N i K B e P B e K T N j i j i K I B e B e b T T N N H H j i j i K I B e b T T N N B e B e N λ − − − − − = − − − − = ⎛ − + ⎞ − = _{⎜ ⎟} ⎝ ⎠ ⎛ − − + ⎞ + _{× ⎜ ⎟} ⎝ ⎠ ⎛ ⎞ ⎛ − − + ⎜ ⎟ ⎜ − _{⎜ ⎟} × _⎜ ⎜ ⎟ ⎜ ⎝ ⎠ ⎝ − = −

∑

∑

⎞⎟_⎟⎟ ⎠ 1 1 1 1 2 1 2 1 1 1 , , 1 , , , , 1 , , , , (2 2) N i N i N N i i N i i b T N N i i i N _{b T bj T} N N N N N S i j i j i i N _{bj T} N N N S j i i i b T b T j i N _N N _N i i b N i N i d B e K T N j i j i K I B e B e b T T N N H H j i j i K I B e b T T N N B e B e H B e λ λ − − − = − − − = ⎛ ⎛ − + ⎞⎞ ⎜ ⎜ ⎟⎟ ⎜ _{⎝ ⎠}⎟ ⎝ ⎠ ⎛ − − + ⎞ + _{× ⎜ ⎟} ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ − − + ⎜ ⎟ ⎜ ⎟ + _{⎜ ⎟} × _{⎜ ⎟} ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ + −

∑

∑

2 2 1 2 1 1 0 1 , , , , N i i N _{bj T} N N N j i i _{T b} i _T j i N N N i K H j i j i I B e b T T S N B e λ− − − − = ⎛ ⎞ ⎛ − − + ⎛ ⎞ ⎜ ⎟ ⎜ ⎜ ⎟ ⎜ ⎟ _{⎝ ⎠} ⎜ ⎜ ⎟ ⎜ ⎝ ⎠ ⎝

∑

_N ⎞⎟_⎟⎟ ⎠ 1

where Is is the same as in equation (10).

For American barrier options, we also recommend a three-point Richardson scheme to improve converge. If the P’s are the values given in equation (15), then the American “up-and out” barrier option price is approximated by

3 2

ˆ 4.5

_A

4

0.5

P

=

P

−

P

+

P

_.

To illustrate the fact, Table 2 reports the values of the early exercise option implied by the decomposition techniques. It is a set of contracts for comparison. Each set consists of sixteen contracts that have different values of the underlying asset price St at valuation date t, the time-to-expiration T, and the

volatility parameter σ. The barrier level H and the strike value K are fixed at 50 and 45, respectively. The risk-free rate r is chosen to be 0.0488. In a set, St =

contracts include out-of-the-money, at-the-money, and in-the-money options. In summary, Table 2 shows that the quasi-analytic pricing formula (11) is accurate [6]. Recently, Hansen and Jorgensen (2000) applied the quasi-analytical formula to the case of floating strike Asian options [7]. The quasi-analytical formula does not have the problem. In the next chapter, we will choose the decomposition technique’s values as our benchmarks.

Table 2

(1) (2) (3) (4) (5) (6) (7)

St σ T European price

Benchmark: Ritchken’s trinomial tree(5000 time steps)

Decomposition Difference 40.0 0.2 0.50 4.7986 5.1828 5.1869 -0.0041 40.0 0.2 1.00 4.7592 5.3797 5.3843 -0.0046 42.5 0.2 0.50 3.1440 3.3443 3.3456 -0.0013 42.5 0.2 1.00 3.2753 3.6403 3.6423 -0.0020 45.0 0.2 0.50 1.8385 1.9331 1.9357 -0.0026 45.0 0.2 1.00 2.0128 2.2111 2.2132 -0.0021 47.5 0.2 0.50 0.8232 0.8609 0.8614 -0.0005 47.5 0.2 1.00 0.9347 1.0215 1.0213 0.0002 40.0 0.4 0.50 6.2435 6.4244 6.4260 -0.0016 40.0 0.4 1.00 6.3540 6.7029 6.7032 -0.0003 42.5 0.4 0.50 4.5514 4.6721 4.6737 -0.0016 42.5 0.4 1.00 4.6727 4.9155 4.9169 -0.0014 45.0 0.4 0.50 2.9602 3.0336 3.0352 -0.0016 45.0 0.4 1.00 3.0586 3.2133 3.2131 0.0002 47.5 0.4 0.50 1.4496 1.4846 1.4851 -0.0005 47.5 0.4 1.00 1.5035 1.5781 1.5780 0.0001

Comparison of the restricted binomial method and the decomposition technique’s values [6] for the early exercise option in an American” up-and-out” put options on non-dividend-paying stocks for one set of contracts computed using different methods. Set I includes 16 contracts, each of which has a different value of the parameter set (St; T; σ). The domain of this parameter set is St = (40; 42:5; 45;

47:5), T = (0.5; 1.0), σ= (0.2; 0.4), the strike price of the put is 45, the barrier level is 50, and the short-term interest rate is 0.0488. Panels (a) shows the numerical results for contract set I, respectively. Columns 1 through 3 represent the values of the parameters, St (the time-t stock price), σ (volatility),

and T (the time to expiration), respectively. Column 4 reports the European option values obtained using the analytic formula in (11). Columns 5 through 6 show the numerical results of option values from the Ritchken method with at least 5,000 time steps (the benchmark) [13], Columns 6 show the numerical result from an analytic approximation technique: the 3-step multi-piece exponential (MPE) approximation with Richardson’s extrapolation.

Chapter 3

The LSM Methodology

This chapter briefly reviews the LSM approach discussed in Longstaff and Schwartz (2001). For more details and a numerical illustration of the algorithm with the help of a simple example, the reader is referred to the original paper.

3.1 The Valuation Framework

Formally, the approach assumes an underlying complete probability space (Ω, F,

P) and finite time horizon [0, T]. The probability space is a triple consisting of

Ω, the set of all possible sample paths (ω), F, the sigma-algebra of events at time T and P, a probability measure defined on the elements of F. Let

,

(

, : ,

)

C ω s t T ω∈ Ω , s∈

( )

t T, denote the path of option cash-flows,

conditional on (i) the option being exercised after t and (ii) the option holder following the optimal stopping strategy at every time after t. The American option is approximated by its Bermuda counterpart, assuming that there are a finite number of exercise dates0< < < ⋅⋅⋅ <t₁ t₁ t_N = . The continuation value T

is equal, under the no-arbitrage conditions, to the risk-neutral expectation of the future discounted cash flows C

(

ω, : ,s t Ti

)

：

1

( , )

[

exp(

j

( , ) ) ( , ; , ) | ]

(16

i N _t i Q _t j i t j i

F

ω

t

E

r

ω

s ds C

ω

t t T F

= +

=

∑

−

∫

)

)

where is the risk-free interest rate and is the information set at

time . The idea underlying the LSM algorithm is that this conditional

expectation can be approximated by a least-squares regression for each exercise date. At time , it is assumed that

(

r ω,s Ft i t 1 N

t ₋ F

(

ω,tN−₁

)

can be expressed as a linear

combination of orthonormal basis functions. This procedure is repeated going back in time until the first exercise date.

Intuitively, in pricing American options, because there exist several possible exercise dates, the holder of the option must decide, at each exercise time, whether to exercise the option or to wait. This decision depends on the comparison between (i) the amount of money that can be obtained if the option is exercised (the immediate exercise value) and (ii) the amount of money that can be obtained if the option is exercised at a future date (the continuation value). The optimal exercise decision, therefore, relies on the estimation of the continuation value. The LSM approach estimates this value by a least-squares regression jointly with the cross-sectional information provided by Monte Carlo simulation. The fitted values of these regressions are then taken as the expected continuation values. Comparing these estimated values with the immediate exercise, the LSM identifies the optimal stopping rule. This procedure is repeated recursively going back in time. Discounting the obtained cash flows to time zero, the price of the American option is found.

American put options. Assume that we are interested in pricing an American put option on a share of stock, where the risk-neutral stock price process follows the stochastic differential equation

d S

=

rS d t

+

σ

S d Z

(1 7 )

where r and σ are constants, Z is a Brownian motion, and the stock does not pay

ercise option

ts per year. dividends. Further assume that the option is exercisable 50 times per year at a strike price of K up to and including the final expiration date T of the option. This type of discrete American exercise feature is sometimes termed a Bermuda exercise feature. As the set of basis functions, we use a constant and the first three Laguerre polynomials. Thus we regress discounted realized cash flows on a constant and three nonlinear functions of the stock price. Since we use linear regression to estimate the conditional expectation function, it is straightforward to add additional basis functions as explanatory variables in the regression if needed. Using more than three basis functions, however, does not materially change the numerical results; in other words, three basis functions are sufficient to obtain effective convergence of the algorithm in this example.

To illustrate the results, Table 3 reports the values of the early ex

implied by both the decomposition and LSM techniques. The value of the early exercise option is the difference between the American put value and that of the European put. The European put value is given by the Black-Scholes formula. This thesis focuses primarily on the early exercise value since it is the most difficult component of an American option’s value to determine; the European component of an American option’s value is much easier to identify.

The LSM estimates are based on 10,000 paths using 50 exercise poin

typically very small. Of the 16 differences shown in Table 3, 13 are less than or equal to one cent in terms of absolute value. In addition, the differences can be both positive and negative. The results show that the LSM algorithm is able to approximate closely the decomposition value. On the other words, the LSM algorithm can verify it, e.g., the decomposition technique and that LSM is more flexible as it can be applied to other problems, like American barrier options.

Table 3

(1) (2) (3) (4 (5) (6) (7)

40 5.

)

St σ T European price Decomposition LSM Difference

.0 0.2 0.50 4.8193 5.2083 2069 0.0014 40.0 0.2 1.00 4.9220 5.5445 5.5374 0.0071 42.5 0.2 0.50 3.2083 3.4192 3.4152 0.0040 42.5 0.2 1.00 3.5809 3.9480 3.9499 -0 -0 .0019 45.0 0.2 0.50 2.0009 2.1118 2.1049 0.0069 45.0 0.2 1.00 2.5308 2.7717 2.7643 0.0074 47.5 0.2 0.50 1.1701 1.2078 1.2188 .0110 47.5 0.2 1.00 1.7408 1.8948 1.8842 0.0106 40.0 0.4 0.50 6.9293 7.1223 7.1202 0.0021 40.0 0.4 1.00 8.0916 8.4540 8.4577 -0 -0 .0037 42.5 0.4 0.50 5.5992 5.7344 5.7329 0.0015 42.5 0.4 1.00 6.9452 7.2394 7.2312 0.0082 45.0 0.4 0.50 4.4759 4.5867 4.5769 0.0098 45.0 0.4 1.00 5.9429 6.1581 6.1599 .0018 47.5 0.4 0.50 3.5432 3.6214 3.6155 0.0059 47.5 0.4 1.00 5.0721 5.2784 5.2528 0.0256

Comparison of the decomposition techniques and simulation values for the early exercise option in an American put option on a share of stock, where the option is exercisable 50 times per year. The early exercise value is the difference between the American and European put values. In this comparison, the strike price of the put is 45, the short-term interest rate is 0.0488, and the underlying stock price S, the volatility of returns σ, and the number of years until the final expiration of the option T are as indicated. The European option values are based on the closed-form Black–Scholes formula. The LSM simulation is based on 10,000 paths for the stock-price process. An analytic approximation technique is the 3-step multi-piece exponential (MPE) approximation with Richardson extrapolation.

3.3 Valuing American Barrier Put Options

tic path-dependent

a final

it not only has an American

e In this section we apply the LSM algorithm to a more exo

option: the American “up-and-out” barrier put option, where the put option can be exercised at any time as long as the stock price has not hit the barrier.

Define the current valuation date as time t, we assume that the option has

expiration date T= (0.5; 1) and that the option can be exercised at any time that the stock price has not hit the barrier H. The risk-neutral dynamics for stock price are the same as in the previous section.

This option is particularly complex because

exercise feature, but the cash flow from exercise is path dependent as the stock price cannot have hit the barrier. In general, these types of problems are very difficult to solve using traditional binomial/trinomial methods. In this case, we can value the option by the LSM. Note that the path dependency of the option payoff does not pose any difficulties to the simulation-based LSM algorithm. Table 4 compares the numerical results from valuing this option by th decomposition technique with those obtained by the LSM. The LSM results are based on 10,000 paths and use 50 exercisable points per year to approximate the continuous exercise feature of the option. As the set of basis functions, we use a constant and the first three Laguerre polynomials to evaluate discount cash flow. As shown in Table 4, differences between the decomposition technique and the LSM are small. The differences in the early exercise values are also small relative to the levels of the American and European option values. These differences would likely be well within the bid-ask spread or transaction cost.

Table 4

(1) (2) (3) (4 (5) (6) (7)

40 5.

)

St σ T European price Decomposition LSM Difference

.0 0.2 0.50 4.7986 5.1869 1817 0.0052 40.0 0.2 1.00 4.7592 5.3843 5.3793 0.0050 42.5 0.2 0.50 3.1440 3.3456 3.3408 0.0048 42.5 0.2 1.00 3.2753 3.6423 3.6402 0.0021 45.0 0.2 0.50 1.8385 1.9357 1.936 2. -0.0003 45.0 0.2 1.00 2.0128 2.2132 2041 0.0091 47.5 0.2 0.50 0.8232 0.8614 0.8763 -0.0149 47.5 0.2 1.00 0.9347 1.0213 1.0007 0.0206 40.0 0.4 0.50 6.2435 6.4260 6.4239 0.0021 40.0 0.4 1.00 6.3540 6.7032 6.6975 0.0057 42.5 0.4 0.50 4.5514 4.6737 4.674 -0.0003 42.5 0.4 1.00 4.6727 4.9169 4.9114 0.0055 45.0 0.4 0.50 2.9602 3.0352 3.0291 0.0061 45.0 0.4 1.00 3.0586 3.2131 3.2088 0.0043 47.5 0.4 0.50 1.4496 1.4851 1.4774 0.0077 47.5 0.4 1.00 1.5035 1.5780 1.5248 0.0532 Comparison of the decomposition techniques [6] and simulation val es for the earlyu exercise option in an American” up-and-out” put options on non-dividend-paying stocks for one set of contracts computed using different methods. Set I includes 16 contracts, each of which has a different value of the parameter set (St; T; σ). The domain of this parameter set is St = (40; 42.5; 45; 47.5), T = (0.5; 1.0), σ= (0.2; 0.4), the strike price of the put is 45, the barrier level is 50, and the short-term interest rate is 0.0488. Panels (a) shows the numerical results for contract set I, respectively. Columns 1 through 3 represent the values of the parameters, St (the time-t stock price), σ (volatility), and T (the time to expiration), respectively. Column 4 reports the European option values obtained using the analytic formula in (11). Columns 5 through 6 show the numerical results of option values from analytic approximation technique: the 3-step multi-piece exponential (MPE) approximation with Richardson extrapolation. Columns 6 show the numerical result from the LSM algorithm based on 10,000 paths for the stock-price process.

.3.1

The Homogeneous Property of American Barrier

For Amer options with a strike level K and a barrier H, the optimal

)

H

t

T

3

Options

ican barrier

exercise boundary has the following property called the homogeneity of degree one in strike and barrier prices [5]:

(

,

)

(

B

_{uo t−}

λ λ

K H

=

λ

B

_{uo t−}

K, ),

∀ >

λ

0,

∈

[0, ] (18

e homogeneity property suggests that among all the contracts considered for

ry, our numerical experiments show that the LSM produces results Th

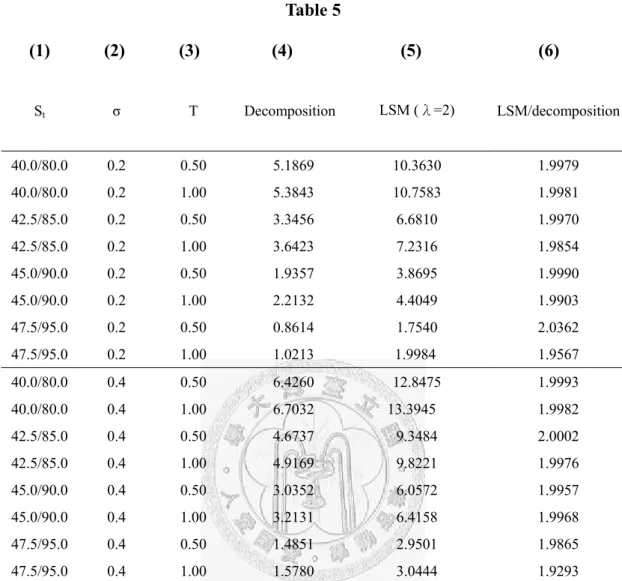
American barrier options and among the contracts with the same proportional value of (K; H), only the boundary for one set of (K; H) needs to be calculated. We use the decomposition technique to price a (K;H) pair and then the LSM to price the ( λ K; λ H ) pair. Then the LSM values should equal the decomposition values timesλ for the homogeneity property to hold. With λ=2, Table 5 confirms that indeed the decomposition results times 2 equal the LSM results.

In summa

consistent with the homogeneity property and that the LSM produces results consistent with the decomposition technique.

Tab 5 (1) (2) (3) (4 (5) (6) St σ T omposition LSM (λ=2) LSM/decomposition 40.0/ .0 0.2 0.50 5. 869 10.3 30 1.9979 le ) Dec 80 1 6 40.0/80.0 0.2 1.00 5.3843 10.7583 1.9981 42.5/85.0 0.2 0.50 3.3456 6.6810 1.9970 42.5/85.0 0.2 1.00 3.6423 7.2316 1.9854 45.0/90.0 0.2 0.50 1.9357 3.8695 1.9990 45.0/90.0 0.2 1.00 2.2132 4.4049 1.9903 47.5/95.0 0.2 0.50 0.8614 1.7540 2.0362 47.5/95.0 0.2 1.00 1.0213 1.9984 1.9567 40.0/80.0 0.4 0.50 6.4260 12.8475 1.9993 40.0/80.0 0.4 1.00 6.7032 13.3945 1.9982 42.5/85.0 0.4 0.50 4.6737 9.3484 2.0002 42.5/85.0 0.4 1.00 4.9169 9.8221 1.9976 45.0/90.0 0.4 0.50 3.0352 6.0572 1.9957 45.0/90.0 0.4 1.00 3.2131 6.4158 1.9968 47.5/95.0 0.4 0.50 1.4851 2.9501 1.9865 47.5/95.0 0.4 1.00 1.5780 3.0444 1.9293

Set I i 32 c h nt value of rameter set (St; ). The

.2

I, respecti

ncludes ontracts, each of whic has a differe the pa T; σ;λ domain of the decomposition parameter set is St = (40; 42.5; 45; 47.5), T = (0.5; 1.0), σ= (0 ; 0.4), the strike price of the put is 45, the barrier level is 50 and the short-term interest rate is 0.0488. The domain of the LSM parameter set is St = (80; 85; 90; 95), T = (0.5; 1.0), σ= (0.2; 0.4), λ=2, the strike price of the put isλ*45, the barrier level isλ*50 and the short-term interest rate is 0.0488. Panels (a) shows the numerical results for contract set vely. Columns 1 through 3 represent the values of the parameters, St /λ*St, σ (volatility), and T (the time to expiration), respectively. Column 4 reports the American up and out barrier put options values obtained using the quasi-analytic approximation in (11) and Column 5 reports the American up and out barrier put options values obtained using the LSM withλ=2. Column 6 shows the ratios of the LSM values divided by the decomposition values.

Chapter 4

Conclusion

options are in widespread use today in the global

s a simple technique, the LSM, to price American puts and Nonstandard or exotic

financial markets. Increasingly, over-the-counter options on many assets including equities, fixed income securities, foreign exchange and commodities have nonstandard characteristics such as the knock-in/knock-out feature, the averaging of the price of the underlying asset, and countless others. Often, due to the lack of liquid secondary markets for these products and in view of their custom-designed nature, an optimal exercise or American feature is incorporated into the design of the contract. It is well-known that even for standard options, the American feature causes problems for valuation because there is no closed-form solution for the prices in general. Therefore, most models of American option valuation are implemented using numerical procedures.

This thesis applie

American barrier options. This approach is intuitive, accurate, and easy to apply. As a framework for valuing and risk managing derivatives, simulation has many important advantages. With the ability to value American options, the applicability of simulation techniques becomes much broader and more promising, particularly for models with multiple factors.

Bib

] Banks, E. Complex Derivatives. Chicago: Probus Publishing, 1994.

roximation of

[3] r with the Binomial

[4] 92, “Alternative Characterizations of

[5] Options," Journal of

[6] g, and Marti G.. Subrahmanyam, 2000, “The Valuation of

[7] cal Valuation of American-Style

[8] Mathematical

[9] Ju, N., 1998, “Pricing an American Option by Approximating Its Early Exercise

[10 , 1990, “The Analytical Valuation of American Options,” Review of

[11 , 2001, “Valuing American Options by Simulations:

liography

[1

[2] Barone-Adesi, G., and R. Whaley, 1987, “Efficient Analytic App American Option Values,” Journal of Finance, 42, 301–320. Boyle, P. and S.H. Lau, 1994, “Bumping Up against the Barrie Method,” Journal of Derivatives, 2, 6–14.

Carr, P., R. Jarrow and R. Myneni, 19

American Put Options,” Mathematical Finance, 2, 87–106. Cheuk, T.H.F., and T.C.F. Vorst, 1996, “Complex Barrier Derivatives,” 4, 8–22.

Gao, B., Jing-Zhi Huan

American Barrier Options Using the Decomposition Technique,” Journal of Economic Dynamics & Control, 24, 1783–1827.

Hansen, A.T. and P.L. Jorgensen (2000), “Analyti

Asian Options,” Management Science, Vol. 46, No. 8, 1116–1136. Jacka, S.D., 1991, “Optimal Stopping and the American Put,” Finance, 1, 1–14.

Boundary as a Piece-Wise Exponential Function,” Review of Financial Studies, 11, 627–646.

] Kim, I.J.

Financial Studies, 3, 547–572. ] Longstaff, F., and E. Schwartz

[12 es,

[13 3,

] Lyuu, Y.-D. 2002, Financial Engineering and Computation: Principl Mathematics, and Algorithms, Cambridge, U.K.: Cambridge University Press. ] Ritchken, P., 1995, “On Pricing Barrier Options,” Journal of Derivatives,