Pattern Formation in Martensitic Thin Films

Pattern formation in martensitic thin films

Y. C. Shua兲 and J. H. Yen

Institute of Applied Mechanics, National Taiwan University, Taipei 106, Taiwan, Republic of China 共Received 4 June 2007; accepted 16 June 2007; published online 10 July 2007兲

Pattern formation in martensitic materials refers to the accommodation problem of how to mix martensitic variants coherently to minimize the strain energy. A framework motivated by energy-minimizing multirank laminated patterns is proposed to study this problem in martensitic films. It is found that the interfaces between the variants of martensite can be quite different in thin films than in bulk materials, and they typically have a simpler structure. Various intriguing and fascinating self-accommodation patterns are predicted for martensitic thin films with different orientations. The results are in good agreement with the Bhattacharya-James thin-film theory 关K. Bhattacharya and R. D. James, J. Mech. Phys. Solids 47, 531 共1999兲兴 as well as with experimental observations. © 2007 American Institute of Physics. 关DOI:10.1063/1.2756320兴 Martensitic materials undergo a first-order diffusionless

phase transformation during which there is a sudden change in the crystal structure at a certain temperature.1A number of recent investigations have suggested that the characteristic distortions of martensite can be exploited to create tiny machines.2The key, then, to achieve the exceptional poten-tial of these materials is to design devices that can take full advantage of the inherent martensitic microstructure. How-ever, while much work has addressed the problem of pattern formation in martensitic bulk crystals, little consideration had given to this phenomenon in martensitic thin films until recently. There are various reasons for that. In particular, the anisotropic and highly nonlinear properties of martensitic materials have made it difficult to develop suitable theories to describe their behavior in slender structures. Bhattacharya and James3 have employed the notion of⌫-convergence to derive a theory of martensitic single crystal films, and Shu4 has extended it to polycrystal films. They have shown that the coherence requirement is weakened in thin films, and this enables a novel strategy for the design of microactuators.5,6 Such a strategy, on the other hand, requires a detailed under-standing of microstructure and its evolution under stress in martensitic films. This in turn calls for an appropriate model that can capture the spirit of the Bhattacharya-James theory while also serving as a convenient tool to evaluate various conditions in design.

The key feature of a martensitic phase transformation is the microstructure it generates. The high-temperature

auste-nite phase is cubic, while the low-temperature martensite

phase has less symmetry. This gives rise to symmetry-related variants, which are identical crystal lattices of martensite with different orientations. The transformation from the aus-tenite to the ith variant of martensite is described by the transformation strain ␧共i兲, and i = 1 , . . . , N where N is the number of martensitic variants. It can be determined from the change of symmetry and lattice parameters. In the case of cubic to trigonal transformation, N = 4 and

␧共1兲₌

冢

冣

冢

冣

冢

冣

冢

冣

where␣ and ␦ are material parameters. Above, the crystal and reference bases are assumed to coincide. Let ␧* _{be a}

macroscopically homogeneous strain. It is recoverable if it can be obtained by a coherent mixture of martensitic vari-ants. Indeed, any recoverable strain in this case can be achieved by a rank-3 laminate of variants;7i.e.,

␧*₌

兺

i=1

4

␥i␧共i兲, 共2兲

where␥iis the global volume fraction of the ith variant and

can be expressed in terms of ␥1=␮1,

␥2=共1 −␮1兲␮2,

共3兲 ␥3=共1 −␮1兲共1 −␮2兲␮3,

␥4=共1 −␮1兲共1 −␮2兲共1 −␮3兲,

and␮jis the local volume fraction of some combinations of

martensitic variants in the jth rank of laminate 共j=1, ... ,N − 1兲. Notice that 兺i=1

N _␥

i= 1. This idea of using an

energy-minimizing multirank laminated microstructure has recently been applied to the study of domain switching in ferroelec-tric crystals under combined electromechanical loadings共see Fig.1 therein8兲.

Instead, let␧*here be interpreted as a locally inhomoge-neous strain; i.e,␧*共x兲 is equal to one of ␧共i兲at each point x. The above multirank laminated structure suggests that this is feasible if each␮j共x兲 is equal to 0 or 1 at each point x. Thus,

when␥k共x兲=1 at x,␥l共x兲=0 if l⫽k. We now use this idea to

study the morphology of martensitic microstructure.

a兲_{Author to whom correspondence should be addressed; electronic address:}

yichung@spring.iam.ntu.edu.tw

APPLIED PHYSICS LETTERS 91, 021908共2007兲

0003-6951/2007/91共2兲/021908/3/$23.00 91, 021908-1 © 2007 American Institute of Physics

Let ␮j共x兲 be relaxed to continuously vary across the

sharp interfaces at the boundaries of martensitic variants. The free energy of a martensite at some fixed temperature below the critical temperature is described in terms of the field variables␮jby I共␮兲 =

冕

兺

subject to the constraint, ⵜ ·␴= 0,

共5兲 ␴= C关␧ − ␧*_{共␮兲兴,}

where ␮=共␮1,␮2, . . . ,␮N−1兲, ␧ is the compatible linear

strain, and C is the elastic modulus and is approximated to be the same for all phases.

Each of the terms in Eq.共4兲has a physical interpretation. The first term with A⬎0, called the interfacial energy den-sity, penalizes changes in the field variables and thus is in-terpreted as the energy of forming a martensitic interface. The second and third terms, with K⬎0, are the anisotropy and elastic energy densities. The sum of these two denotes the energetic cost that the crystal must pay if the field vari-ables and strain deviate from the preferred states; thus, this builds in the information that the crystal prefers a certain spontaneous strain.

We postulate that the martensitic microstructure is ob-tained by minimizing the total free energy in Eq.共4兲 under the constraint in Eq. 共5兲. However, it is not an easy task. Alternatively, the energy is decreasing if it follows the path9

⳵␮ ⳵t = − L

␦I

␦␮= LF, 共6兲

where L⬎0 is the mobility and F=−␦I/␦␮ is the

thermo-dynamic driving force defined by the variational derivative of

the free energy. It is equal to Fint_{+ F}a_{+ F}elas_{, where F}int

= 2Aⵜ2_{␮ is the driving force for the coarsening of}

micro-structure, Fa= −⳵Wa共␮兲/⳵␮is the driving force for setting␮

as much close to the lowest points in the energy wells as possible, and Felas_{= C关␧−␧}*_{共␮兲兴·⳵␧}*_{共␮兲/⳵␮ is the driving}

force for the refinement of microstructure to accommodate the boundary constraints.

The present method is different from the conventional phase field models developed by Jin et al.,10 Lookman

et al.,11Salje et al.,12 Slutsker et al.,13and Li et al.,14,15for martensitic and ferroelectric microstructure evolutions. Their approaches choose a suitable set of order parameters and the special polynomial expansions of them at high orders for a particular transformation. Instead, we choose a set of field variables motivated by the hierarchical structure of multirank laminates as in Eq.共3兲. Besides, the anisotropy energy den-sity Wa共␮兲 in Eq. 共4兲is explicitly given irrespective of dif-ferent types of martensitic transformation under consider-ation.

We now apply Eq.共6兲 to the study of pattern formation in martensitic thin films undergoing cubic to trigonal trans-formation at a fixed temperature below the critical one. Therefore, the influence of the austenite variant is insignifi-cant here. We consider a martensitic single crystal film re-leased from the substrate but constrained on its lateral boundaries. Suppose the thickness of the film is much smaller than the lateral extent. In this situation, Bhattacharya and James3 have shown that the out-of-plane strain incom-patibility can be neglected. Therefore, we need to consider only the in-plane components of the transformation strains ␧共i兲 _{in Eq. 共1兲. Let R}

共001兲, R共110兲, and R共111兲 be the proper

rotations that map 共001兲关11¯0兴, 共110兲关11¯0兴, and 共111兲关11¯0兴 back to the identity. Therefore, the transformation strains in the reference basis become R_共001兲␧共i兲R_共001兲T , R_共110兲␧共i兲R_共110兲T , and R_共111兲␧共i兲R_共111兲T for i = 1 , . . . , 4. The matrices containing the in-plane components of the above transformation strains are denoted by␧_共001兲共i兲 ,␧_共110兲共i兲 , and␧_共111兲共i兲 .

We use Ti–Ni in the R phase as the representative mate-rial. This gives␣= 0 and␦= 0.0047 in Eq. 共1兲.16The elastic moduli of Ti–Ni single crystals are not available, therefore, we take C11= C22= 80 GPa, C12= 20 GPa, C66= 30 GPa, and C₁₆= C₂₆= 0 共Voigt notation兲, which are typical parameters for Ti–Ni polycrystals. The present formulation involves only two parameters. The first one A is related to the length TABLE I. Compatible interfacial normals in共110兲 films.

Variants 1, 2 or 1, 3 1, 4 2, 4 or 3, 4

兵100其 type 共1,0兲 共0,1兲 共1,0兲

兵110其 type 共1,冑2兲 共1,0兲 共−1,冑2兲

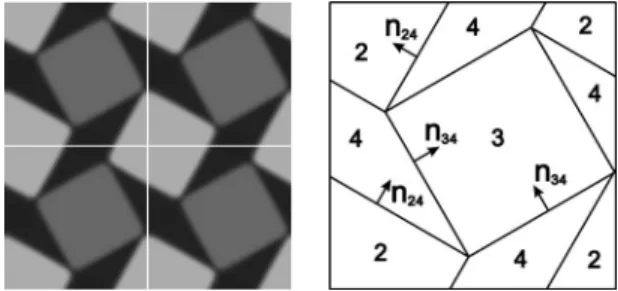
FIG. 2. Self-accommodation pattern in共110兲 films. FIG. 1. LHS and RHS are self-accommodation patterns in共001兲 and 共111兲

films. As periodic conditions are taken in the simulations, four identical patterns are packed together to obtain a better image.

021908-2 Y. C. Shu and J. H. Yen Appl. Phys. Lett. 91, 021908共2007兲

scale of the microstructure and can be grouped to a dimen-sionless parameter D =共A/K兲/l02, where l0 is the size of the

simulation. We take D = 0.0001.17 The other parameter K is chosen such that the energy densities Wa_{and W}elas_{are of the}

same order. The periodic boundary conditions are taken for simulations, and the fast Fourier transform is employed to enhance the speed of computation. As the nucleation prob-lem is not considered in the present study,10,18 we take the random initial conditions.19

For共001兲 films, variants 1 and 4 and variants 2 and 3 are indistinguishable, since␧_共001兲共1兲 =␧_共001兲共4兲 and␧_共001兲共2兲 =␧_共001兲共3兲 . There-fore, there are only two distinct variants, and the self-accommodation pattern is the lamellar type, as shown in the left-hand side共LHS兲 of Fig.1, where different variants are presented by different gray levels. While such a lamellar pat-tern is not a basic unit for self-accommodation in bulk trigo-nal martensites,20it holds true in thin films since the in-plane average of transformation strains is zero. As a result, this pattern is commonly observed in many共001兲 trigonal films.21 For 共110兲 films, variants 2 and 3 are indistinguishable, since ␧_共110兲共2兲 =␧_共110兲共3兲 . Therefore, there are three distinct vari-ants. In a bulk trigonal martensite, there are two typical in-terfaces: one is兵100其 type and the other is 兵110其 type. The corresponding interfacial normals predicted based on the Bhattacharya-James thin-film theory are listed in TableI. The simulation results give two distinct patterns. The first one, in Fig.2, is similar to the commonly observed “herring-bone⬙ pattern in trigonal martensites.20 Another simpler pattern is shown in the LHS of Fig.3, which is not an allowable pat-tern in bulk martensites, since the third components in the interfacial normals are different, as can be seen in the right-hand side共RHS兲 of Fig.3. However, it is a legitimate one in thin films, and this confirms that martensitic materials can

form many more interfaces in a thin film than in bulk. In addition, the interfacial normals in these two simulations agree very well with those listed in TableI.

For共111兲 films, all of the in-plane transformation strains are different in this case, and a self-accommodation pattern containing all of these four martensitic variants is shown in the RHS of Fig. 1. Next, to see how the microstructure evolves under stress, consider a biaxial tension␴*=␴0I

ap-plied in the plane of the film, where ␴0⬎0 and I is the

identity matrix. This case is important since these films are typically stressed under pressure when used in micropumps. Figure4shows the coalescence of martensitic variants under stress. Variant 1 disappears and the volume fractions of phases 2, 3, and 4 are identical. This can be explained by an energetic argument: −␴*·␧_共111兲共2兲 = −␴*·␧_共111兲共3兲 = −␴*·␧_共111兲共4兲 ⬍0 while −␴*·␧_共111兲共1兲 ⬎0. Finally, according to Table II, the sulting morphology evolves along a compatible path to re-duce the strain energy.

The authors are glad to acknowledge the financial sup-port of the National Science Council of Taiwan under Grant No. 95-2221-E-002-166.

1_{S. K. Wu and H. C. Lin, Mater. Chem. Phys. 64, 81共2000兲.} 2_{K. Bhattacharya and R. D. James, Science 307, 53共2005兲.}

3_{K. Bhattacharya and R. D. James, J. Mech. Phys. Solids 47, 531共1999兲.} 4_{Y. C. Shu, Arch. Ration. Mech. Anal. 153, 39共2000兲.}

5_{K. Bhattacharya, A. DeSimone, K. F. Hane, R. D. James, and C. J.}

Palmstrøm, Mater. Sci. Eng., A 273-275, 685共1999兲.

6_{Y. C. Shu, Mater. Trans. 43, 1037共2002兲.}

7_{K. Bhattacharya, Continuum Mech. Thermodyn. 5, 205共1993兲.} 8_{Y. C. Shu, J. H. Yen, J. Shieh, and J. H. Yeh, Appl. Phys. Lett. 90, 172902}

共2007兲.

9_{Y. C. Shu, M. P. Lin, and K. C. Wu, Mech. Mater. 36, 975共2004兲.} 10_{Y. M. Jin, A. Artemev, and A. G. Khachaturyan, Acta Mater. 49, 2309}

共2001兲.

11_{T. Lookman, S. R. Shenoy, K. Ø. Rasmussen, A. Saxena, and A. R.}

Bishop, Phys. Rev. B 67, 024114共2003兲.

12_{E. K. H. Salje, H. Zhang, D. Schryvers, and B. Bartova, Appl. Phys. Lett.}

90, 221903共2007兲.

13_{J. Slutsker, A. Artemev, and A. L. Roytburd, J. Appl. Phys. 91, 9049}

共2002兲.

14_{Y. L. Li, S. Y. Hu, Z. K. Liu, and L. Q. Chen, Appl. Phys. Lett. 78, 3878}

共2001兲.

15_{Y. L. Li, S. Y. Hu, Z. K. Liu, and L. Q. Chen, Appl. Phys. Lett. 81, 427}

共2002兲.

16_{S. Miyazaki, S. Kimura, and K. Otsuka, Philos. Mag. A 57, 467共1988兲.} 17_{A. Artemev, Y. Jin, and A. G. Khachaturyan, Acta Mater. 49, 1165}

共2001兲.

18_{K. Dayal and K. Bhattacharya, Acta Mater. 55, 1907共2007兲.}

19_{K. Ø. Rasmussen, T. Lookman, A. Saxena, A. R. Bishop, R. C. Albers,}

and S. R. Shenoy, Phys. Rev. Lett. 87, 055704共2001兲.

20_{T. Fukuda, T. Saburi, K. Doi, and S. Nenno, Mater. Trans., JIM 33, 271}

共1992兲.

21_{S. K. Streiffer, C. B. Parker, A. E. Romanov, M. J. Lefevre, L. Zhao, J. S.}

Speck, W. Pompe, C. M. Foster, and G. R. Bai, J. Appl. Phys. 83, 2742 共1998兲.

TABLE II. Compatible interfacial normals in共111兲 films.

Variants 1, 2 1,3 1,4 2,3 2,4 3,4

兵100其 type 共冑3 , 1兲 共−冑3 , 1兲 共0,1兲 共0,1兲 共−冑3 , 1兲 共冑3 , 1兲 兵110其 type 共冑3 , 1兲 共−冑3 , 1兲 共0,1兲 共1,0兲 共1,冑3兲 共1,−冑3兲

FIG. 3. Another possible self-accommodation pattern in共110兲 films.

FIG. 4. Pattern in共111兲 films under biaxial tension.

021908-3 Y. C. Shu and J. H. Yen Appl. Phys. Lett. 91, 021908共2007兲