A Hybrid Data Mining Approach for Analysis of Patient Behaviors in RFID Environments

A Hybrid Data Mining Approach for Analysis of Patient Behaviors in RFID

Environments

Vincent S. Tseng

1

, Eric Hsueh-Chan Lu

1

, Chia-Ming Tsai

1

, and Chun-Hung Wang

2 1

Department of Computer Science and Information Engineering

National Cheng-Kung University, Tainan, Taiwan, R.O.C.

2

Institute for Information Industry

1

tsengsm@mail.ncku.edu.tw,

2

mars@iii.org.tw

Abstract

In this paper, we propose a novel hybrid approach named Hybrid Behavior Pattern Mine (HBP-Mine) for analysis of patient behaviors by mining the RFID movement log. We first discover more about the regular behavior models using data mining techniques, then calculating the variation between different periods of regular behavior model. A number of studies have been done on the variations of association rule and sequential pattern in the past few years. In our approach, we are not only based on the variations of these two behavior patterns, but also integrated the other three kind of new behavior patterns using the weighted method. Finally, we conducted a series of experiments to evaluate the rationality of the proposed hybrid method under different system conditions by varying the parameters.

Keywords: Data Mining, RFID, Association Pattern, Sequential Pattern, Patient Monitoring.

1. Introduction

With the progress of RFID (Radio Frequency Identification) [7] techniques, many applications have been proposed [8], [15], and one of the very interesting applications is precisely positioning for objects. The object positioning can be achieved by using the RFID Readers to read the position of objects that attach RFID Tags. In the area of object positioning, the widely used techniques are RFID and GPS. In this research, we use RFID to position the objects instead of GPS with the reasons listed as follows: 1) the cost of RFID Tag is cheap, 2) the size of RFID Tag is small, 3) it is easy to carry, and 4) the RFID positioning can be used in the buildings. Obviously, the RFID techniques are suitable for in-door object monitoring applications.

Consider an in-door patient-care application. In the past, if a doctor needs to observe the drug treatment for the patients, the doctor must spend the whole day aside the patient and record the patient’s behavior. The

collected information is then used by the doctor to determine the patient’s physical and mental condition evaluation. However, this needs a lot of human efforts for collecting the patients’ behavior information. In our research, we use RFID Readers and Tags to record the patient behaviors without the help of the humans to save the human resources. After collecting the patients’ behaviors for a period of time, we can establish the regular model for the patients by utilizing data mining techniques. In this way, the doctor is able to know the behavior changes of certain patient after the drug treatment by comparing the behavior differences between the patient’s current behavior and the regular model. In addition, the patient’s behavior can also be monitored to automatically warn the doctor in real-time if the behavior of the patient is abnormal. Establishing this kind of systems will be very helpful for patient health care and human resource saving.

Based on the motivation, we first use RFID techniques to monitor the behavior of patients and afterwards we devise the novel data mining methods for the discovery of patient patterns. In the drug treatment monitoring applications, the doctors pay their attention to the pattern changes after the treatment. Therefore, we propose a set of data mining methods for discovering the information of pattern changes.

In recent years, the association rules and sequential patterns are the popular issues in data mining field. For the research on behavior pattern mining, number of studies have been proposed to discover this kind of interesting patterns from transaction database [2], [3], [6], [9], [12]. In [2], Agrawal first proposed a method named Apriori for fast mining of the association rules from transaction databases. In [9], Han proposed a tree-based method named FP-Tree for discovery of the association rules without candidate generation. The issue of sequential pattern mining was explored in [3]. The behavior patterns include four types in terms of Association Pattern (AP) [2], [9], Sequential Pattern (SP) [3], Navigation Pattern (NP) [4].

In the discovery of pattern changes, some of the past studies focused on association patterns and sequential

patterns respectively [5], [10], [11], [14], [13]. In addition, there exist very few studies talk about integrate varies variations of behavior pattern. Generally, the variation of pattern sets is to calculate the difference of structure or support. In [14], the authors proposed a distance measurement for two closed frequent patterns. In [13], the authors proposed the alignment algorithm to align two sequences with different length. In order to apply alignment algorithm to sequential pattern, some researches modify the penalty functions in terms of insertion, deletion, and substitution [5], [10].

The rest of this paper is structured as follows. In Section 2, we state the proposed system architecture. The details of the proposed data mining methods are described in Section 3. The empirical performance evaluation for the proposed methods is made in Section 4. The conclusions and the future work are given in Section 5.

2. System Architecture

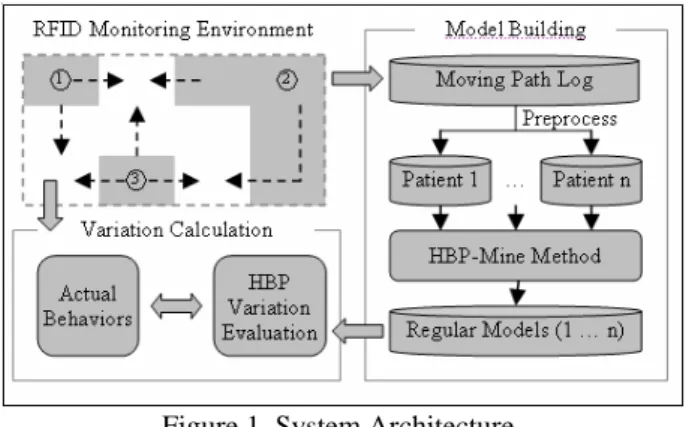
Figure 1 shows the system architecture. The RFID Readers and Tags are used to record the moving log of patients, the store the log to the database. After a period of time, the moving log for each patient is collected. Then, we can establish the regular model for each patient by using our proposed data mining method named HBP-Mine. Finally, we can evaluate the variation between regular models and current behaviors for each patient. The results can provide the valuable information for the doctors to determine whether the drug treatment is effective or not.

Figure 1. System Architecture.

3. Proposed Method

In this section, we describe the proposed method for calculating variations of behavior patterns in RFID environments. The main purpose of this method is to calculate the whole deviation for two consecutive movement logs which are divided by check point. In our

follows: 1) Association Patterns, 2) Sequential Patterns, and 3) Location Change Frequency/Velocity.

3.1 Variation of Association Patterns

The variation of association patterns can be divided into two parts, 1) structure variation, and 2) support variation.

Definition 1: Let p1 and p2 be two closed patterns. The

structure variation (Vstr) of association patterns p1 and p2 is defined as (1).

(

)

2 1 2 1 2 1

,

1

p

p

p

p

p

p

V

_str

U

I

−

=

(1)

Definition 2: Let s1 and s2 be two supports of closed patterns. The support variation (Vsup) of association patterns s1 and s2 is defined as (2).

(

)

₍

₎

max( , ) 1 2 2 1 2 1 2 1 sup

log

1 2

,

max

,

s

s

s

s

s

s

s

s

V

=

−

×

_{s s}

−

(2)

The pattern variation of two association closed patterns (Vap) is to combine structure variation and support variation with a weight as (3), where w1 + w2 = 1.

(

p

1

,

p

2

)

w

1

V

(

p

1

,

p

2

)

w

2

V

sup

(

s

1

,

s

2

)

V

ap

=

×

str

+

×

(3)

Definition 3: Let A1 = {p1, p2, …, pn}, A2 = {p1’, p2’, …, pm’} be two sets of closed pattern, and si be the support of pi. A pattern pi’ in A2 is a couple pattern for pattern pk in A1 (denote to c(pk) = pi’), if and only if there exists no pattern pj’ in A2 such that Vap(pk, pj’) < Vap(pk, pi’), where 1 ≤ j ≤ m and i ≠ j.

Furthermore, we extend the variation of two closed patterns to the variation of two closed pattern sets. We evaluate the variation of two pattern sets by using the bipartite graph. For each pattern p in a set, we find the most similar pattern c(p) in another set named couple pattern. The variation of two pattern sets (VAP) is as shown in (4). The function rsup is defined as Σsup(pj) / sup(pi), ∀pj∈A1.

( )

(

)

(

)

(

(

( )

)

)

2

,

'

'

,

'

,

,

1 sup 2 1 sup 1

∑

∑

= =

+

=

m j j j j ap n i i i i ap AP

A

p

r

p

c

p

V

A

p

r

p

c

p

V

V

(4)

0.5. Figure 2-(c) shows the couple relation of A1 and A2. The variation of A1 and A2 is 0.31.

Figure 2. Example of the variation on association pattern sets.

3.2 Variation of Sequential Patterns

The variation of sequential patterns can be divided into structure variation and support variation. The support variation is the same as (2) and the pattern variation is the same as (3).

Definition 4: Let s1 and s2 be two sequential patterns. The

structure variation (Vstr) of sequential patterns s1 and s2 is defined as (5).

(

s1,s2

)

1 Alignment

(

s1,s2

)

V_str = − (5) In alignment algorithm, we modify the penalty function in terms of insertion, deletion, and substitution. Figure 3 shows the algorithm for aligning sequential patterns. Initially, the penalty is set as the inverse of sequence length (line 1) and then the matrix is initialized (line 2 to line 6). We use dynamic programming to decide Mi,j (line 7 to line 12). Finally, Mn, m is returned as the similarity of the two sequential patterns (line 13).

Figure 3. Algorithm for sequential pattern alignment.

Example 2: Let s1 and s2 be two sequential patterns. s1 = {A, C, D, G, T, K} and s2 = {C, B, G, T, K}. The penalty of insertion or deletion is 1 / (6 + 5) = 0.9. Table 1 shows the detailed alignment process of s1 and s2. The structure variation of s1 and s2 is Vstr(s1, s2) = 1 - 0.73 = 0.27.

Table 1. Alignment between s1 and s2.

The variation of sequential patterns (VSP) is similar to association patterns (4). At fist, we find the couple relation of two sequential pattern sets. Then, the variations of every pairs of couple patterns are normalized. The final results can be represented by the variation of sequential patterns.

3.3 Variation of Location Change Frequency and

Velocity

In this paper, location change frequency (LCF) is defined as the average count of patient movement and location change velocity (LCV) is defined as the average speed of patient movement everyday. LCF and LCV are both variations of two real numbers like the support variation. Note that we consider not only variation ratio but also the variation quantity. The formal definitions are given as below.

Definition 5: Let (f1, v1) and (f2, v2) be two pairs of location change frequency and velocity. The location

change variation of (f1, v1) and (f2, v2) is defined as (6).

(

)

(

)

(

)

2 , , , , , _{1 2 2} sup 1 2 sup 1 2 1 v v V f f V v f v f V_LC = + (6)

Example 3 Suppose f1 is set as 60 and v1 is set as 100. Figure 4 shows the variation distributions of location change frequency f2 and velocity v2.

Figure 4. Variation distribution of location change.

3.4 Integrated Variations of Behavior Patterns

We have introduced all of the behavior patterns we used in this paper. Because all of the variations of behavior pattern are from 0 to 1, we utilize the expert domain knowledge to combine the three types of behavior patterns with the weighting strategy. The variation of two logs can be formulated as (7), where w1 + w2 + w3 = 1.

LC SP AP w V w V V w V= ₁× + ₂× + ₃× (7)

4. Experimental Evaluation

In this section, we conducted a series of experiments to evaluate the performance for the proposed method namely HBP-Mine under different system conditions by varying the parameters in terms of minimal support, close pattern set, activity and event probability. We employ Visual C++ to implement our experiments on a 3.0 GHz machine with 1 GB of memory running windows XP.

Table 2 : Major parameters of the simulation model.

4.1 Simulation Model

Table 2 shows the major parameters of the simulation model. We design a simulation model in NCKU hospital - Mental Health Center [16]. This detection center consists of four floors with 49 regions. We use activity and event probability to represent the characteristic of a patient.

event probability represents the moving habit of patients. Table 3 shows six distinct models of patient types. There are 30 simulated patients within the center (5 patients for each model). Figure 5 shows the movement model of patients. We generated 30 days of data used for training to obtain regular models and 150 days of data used for evaluation.

Figure 5. Movement model of simulation.

Table 3. Major models of patient type.

4.2 Impact of varying minimal support threshold

This experiment analyzes the execution time when varying the minimal support threshold in pattern mining phase. Figure 6 shows that the execution time of navigation pattern mining and the execution time of sequential pattern mining are both invariant. We also observe that the execution time of association pattern mining increases with the decrease of the minimal support threshold.

Figure 6. Execution Time with minimal support varied.

4.3 Impact of different patient type models

This experiment analyzes the variation under different patient type models. Table 4 shows that the variation is the smallest when it is calculated by the same models.

and event probability, so behavior patterns are similar. In particular, we observed that the variation of type 1 and type 4 is smaller then those of the other combinations of models. The reason is that type 1 and type 4 are with the same activity, which leads the amount of behavior patterns to be more similar than others.

Table 4. Variations with different patient type models.

4.4 Impact of varying activity and event

probability

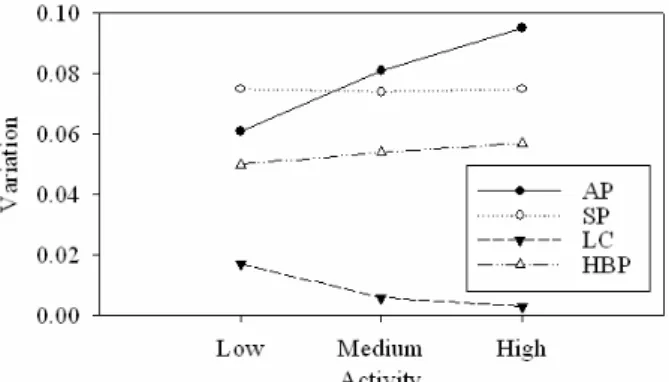
This experiment analyzes the variation when varying the activity and the event probability. Figure 7 shows the impact on variation by varying the activity and Figure 8 shows the impact when varying the event probability. We observed that: 1) for AP, the variation increases when the activity increases or the event probability decreases, 2) for SP, the variation decreases when the event probability increases, 3) for LC, the variation decreases when the activity increases, and 4) for HBP, the variation increases when the activity increases or the event probability decreases. Based on experimental results, we can obtain that when the behaviors of patients are more regular, the variations of behavior patterns are more similar.

Figure 7. Variation with activity varied.

Figure 8. Variation with event probability varied.

5. Conclusions And Future Work

In this paper, we have proposed a novel hybrid approach named HBP-Mine based on the combination of behavior patterns for efficient behavior pattern mining and rational variation evaluating by mining the RFID log in RFID monitoring environments. Although there exist lots of studies exploring various research topics of behavior pattern mining, few of them discussed the variation issue between two behavior pattern sets. To our best knowledge, this is the first work aiming at the goal of rational variation evaluating and calculating with the consideration of efficiently mining issue simultaneously.

To evaluate the performance of the proposed method, we designed a simulator reflecting a reasonable movement model in real mental health center and conducted a series of experiments. The evaluation can be divided into two parts, 1) behavior pattern mining, and 2) variation evaluation. For the behavior pattern mining, the minimal support is varied to evaluate the execution time of HBP-Mine, and it is shown that our method is scalable under different minimal support. For the variation evaluation, we observed that HBP-Mine calculates lower variation does under lower activity or higher event probability. The above experiments demonstrate that our proposed methods are efficient and rational under different kinds of system conditions.

As to the future work, because the real movement data of patient RFID environments is difficult to obtain, we will deploy a patient RFID environment to collect the movement data. In addition, we will apply the HBP-Mine on other applications like amusement park, with the aim to discover the variation of behavior patterns in RFID environments.

6. Acknowledgement

This research was supported by National Science Council, Taiwan, R.O.C., under grant no.

NSC95-2218-E-006-020 and Institute for Information Industry, under grant no. IA96H01313E04(W5).

7. References

[1] R. Agrawal, T. Imielinski, and A. Swami “Mining association rules between sets of items in large databases.” In Proc. of the ACM SIGMOD, pages 207–216, May 1993. [2] R. Agrawal and R. Srikant ”Fast algorithms for mining

association rules.” In Proc. of the 20th VLDB pages 478-499, 1994.

[3] R. Agrawal and R. Srikant “Mining sequential pattems.” In Proc. 1995 Int. Conf. Data Engineering (ICDE’95), pages 3-14, Taipei, Taiwan, Mar. 1995.

[4] J. Borges and M. Levene, Data Mining of User Navigation Patterns. Proc. of the Workshop on Web Usage Analysis and User Profiling (WEBKDD’ 99), pages 31-36. August 15, 1999, San Diego, CA.

[5] Matthieu Capelle, Cyrille Masson, and Jean-Francois Boulicaut “Mining Frequent Sequential Patterns under a Similarity Constraint.” IDEAL 2002: 1-6.

[6] David Wai-Lok Cheung, Jiawei Han, Vincent T. Y. Ng, Ada Wai-Chee Fu, Yongjian Fu “A Fast Distributed Algorithm for Mining Association Rules.” PDIS 1996: 31-42

[7] Fanberg. H., "The RFID Revolution," Marketing Health Services, vol. 24, no. 3, 2004, pp. 43-44.

[8] Jiawei Han, Hector Gonzalez, Xiaolei Li, Diego Klabjan “Warehousing and Mining Massive RFID Data Sets.” ADMA 2006: 1-18.

[9] Jiawei Han, Jian Pei, Yiwen Yin, Runying Mao “Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach.” Data Min. Knowl. Discov. 8(1): 53-87 (2004).

[10] Hye-Chung(Monica) Kum, Joong Kyuk Chang, and Wei Wang “Sequential Pattern Mining in Multi-Databases via Multiple Alignment.” Data Min. Knowl. Discov. 12(2-3):151-180, 2006.

[11] P. Moen “Attribute, Event Sequence, and Event Type Simarity Notions for Data Mining.” PhD thesis, Dept. of Computer Science, University of Helsinki, Finland, February 2000.

[12] N. Pasquier, Y. Bastide, R. Taouil, and L. Lakhal “Discovering frequent closed itemsets for association rules.” Proceedings of 7th International Conference on Database Theory (ICDT’99), 1999.

[13] Altschul S.F., Gish W, Miller W, et al. “ Basic local alignment search tool. ＂ Journal of Molecular Biology, 215: 403～410, 1990

[14] Dong Xin, Jiawei Han, Xifeng Yan, Hong Cheng “Mining Compressed Frequent-Pattern Sets.” VLDB 2005: 709-720. [15] Shang-Wei Wang, Wun-Hwa Chen, Chorng-Shyong Ong,

Li Liu, Yun-Wen Chuang “RFID Application in Hospitals: A Case Study on a Demonstration RFID Project in a Taiwan Hospital.” HICSS 2006

[16] Mental Health Center of National Cheng Kung University Hospital. URL: http://www.carehouse.org.tw/