This article was downloaded by: [National Chiao Tung University 國立交 通大學]
On: 27 April 2014, At: 22:53 Publisher: Taylor & Francis
Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer House, 37-41 Mortimer Street, London W1T 3JH, UK
Applied Artificial
Intelligence: An
International Journal
Publication details, including instructions for authors and subscription information: http://www.tandfonline.com/loi/uaai20
A new method for
generating fuzzy rules from
numerical data for handling
classification problems
Shyi-Ming Chen , Shao-Hua Lee & Chia-Hoang Lee
Published online: 30 Nov 2010.
To cite this article: Shyi-Ming Chen , Shao-Hua Lee & Chia-Hoang Lee (2001) A new method for generating fuzzy rules from numerical data for handling classification problems, Applied Artificial Intelligence: An International Journal, 15:7, 645-664, DOI: 10.1080/088395101750363984
To link to this article: http://dx.doi.org/10.1080/088395101750363984
PLEASE SCROLL DOWN FOR ARTICLE
Taylor & Francis makes every effort to ensure the accuracy of all the information (the “Content”) contained in the publications on our platform. However, Taylor & Francis, our agents, and our licensors make no representations or warranties whatsoever as to the accuracy, completeness, or suitability for any purpose of the Content. Any opinions and views expressed in this publication are the opinions and views of the authors, and are not the views of or endorsed by Taylor & Francis. The accuracy of the Content should not be relied upon and should be independently verified with primary sources of information. Taylor and Francis shall not be liable for any losses, actions, claims,
connection with, in relation to or arising out of the use of the Content. This article may be used for research, teaching, and private study purposes. Any substantial or systematic reproduction, redistribution, reselling, loan, sub-licensing, systematic supply, or distribution in any form to anyone is expressly forbidden. Terms & Conditions of access and use can be found at http://www.tandfonline.com/page/terms-and-conditions
Applied Arti® cial Intelligence, 15:645± 664, 2001 Copyright # 2001 Taylor & Francis 0883-9514 /01 $12.00 ‡.00
&
A NEW METHOD FOR
GENERATING FUZZY RULES
FROM NUMERICAL DATA
FOR HANDLING
CLASSIFICATION PROBLEMS
SHYI -MING CHENDepartment of Computer Science and Information Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan, Republic of China
SHAO-HUA LEE and CHIA-HOANG LEE
Department of Computer and Information Science, National Chiao Tung University, Hsinchu, Taiwan, Republic of China
Fuzzy classi® cation is one of the important applications of fuzzy logic. Fuzzy classi® cation Systems are capable of handling perceptual uncertainties, such as the vagueness and ambiguity involved in classi® cation problems. T he most important task to accomplish a fuzzy classi® cation system is to ® nd a set of fuzzy rules suitable for a speci® c classi® cation problem. In this article, we present a new method for generating fuzzy rules from numerical data for handling fuzzy classi® cation problems based on the fuzzy subsethood values between decisions to be made and terms of attributes by using the level threshold value ¬ and the applicability threshold value , where ¬ 2 [0;1] and 2 [0;1]. W e apply the proposed method to deal with the ``Saturday Morning Problem,’’ where the proposed method has a higher classi® cation accuracy rate and generates fewer fuzzy rules than the existing methods.
Fuzzy classi® cation is one of the important applications of fuzzy logic (Zadeh, 1965, 1988). In a fuzzy classi® cation system (Yoshinari, Pedrycz, & Hirota, 1993), a case can properly be classi® ed by applying a set of fuzzy rules based on the linguistic terms (Zadeh, 1975) of its attributes. Fuzzy classi® cation systems are capable of handling perceptual uncertainties, This work was supported by the National Science Council, Republic of China, under Grant NSC 89-2213-E-011-060.
Address correspondence to Professor Shyi-Ming Chen, Ph.D., Department of Computer Science and Information Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan, R.O.C. E-mail: smchen@et.ntust.edu.tw
645
such as the vagueness and ambiguity involved in classi® cation problems (Yuan & Shaw, 1995). The most important task to accomplish a fuzzy clas-si® cation system is to ® nd a set of fuzzy rules suitable for a speci® c classi-® cation problem. Usually, we have two methods to complete this task. One approach is to obtain knowledge from experts and translate their knowledge directly into fuzzy rules. However, the process of knowledge acquisition and validation is di cult and time-consuming. It is very likely that an expert may not be able to express his or her knowledge explicitly and accurately. Another approach is to generate fuzzy rules through a machine-learning process (Castro & Zurita, 1997; Chen & Yeh, 1998; Chen, Lee, & Lee, 1999; Hayashi & Imura, 1990; Hong & Lee, 1996; Klawonn & Kruse, 1997; Nozaki, Ishibuchi, & Tanaka, 1997; Wang & Mendel, 1992; Wu & Chen, 1999, Yuan & Shaw, 1995; Yuan & Zhuang, 1996), in which knowledge can be automatically extracted or induced from sample cases or examples. In Castro and Zurita (1997) an inductive learning algorithm in fuzzy systems is presented. In Chen and Yeh (1998) we have presented a method for generating fuzzy rules from relational database systems for estimating null values. In Hayashi and Imura (1990) a method to automatically extract fuzzy if-then rules from a trained neural network is presented. In Hong and Lee (1996) an algorithm to induce fuzzy rules and membership functions from training examples is presented. In Klawonn and Kruse (1997) a method for constructing a fuzzy controller from data is presented. In Nozaki, Ishibuchi, and Tanaka (1997) a heuristic method for generating fuzzy rules from numerical data is presented. In Wang and Mendel (1992) an algorithm for generating fuzzy rules by learning from examples is presented. In Wu and Chen (1999), we have presented a method for constructing membership func-tions and fuzzy rules from training examples. In Yuan and Zhuang (1996) a genetic algorithm for generating fuzzy classi® cation rules from training examples is presented.
A commonly used machine-learning method is the induction of decision trees (Quinlan, 1994) for a speci® c problem. The method of decision trees induction has been expanded to induce fuzzy decision trees proposed by Yuan and Shaw (1995), where fuzzy entropy is used to lead the search of the most e ective decision nodes. However, the method presented in Yuan and Shaw (1995) has some drawbacks, i.e., (1) it generates too many fuzzy rules and (2) its classi® cation accuracy rate is not good enough.
In this article, we present a new method based on the ® ltering of the fuzzy subsethood values (Kosko, 1986; Yuan & Shaw, 1995) between decisions to be made and terms of attributes by the level threshold value ¬ and the applicability threshold value for generating fuzzy rules from the numerical data in a more e cient manner, where ¬ 2 [0;1] and 2 [0;1]. We apply the proposed method to deal with the Saturday Morning Problem (Yuan & Shaw, 1995), where the proposed method has higher classi® cation accuracy
and generates fewer fuzzy rules than the one presented in (Yuan & Shaw, 1995).
FUZZY SET THEORY
In 1965, Zadeh proposed the theory of fuzzy sets (1965). Let U be a universe of discourse, where U ˆ {u1;u2; . . . ;un}. A fuzzy set A of the universe of discourse U can be represented by
A ˆX n iˆ1
·A…ui†=ui
ˆ ·A…u1†=u1‡ ·A…u2†=u2‡ ¢ ¢ ¢ ‡ ·A…un†=un; …1† where ·A is the membership function of the fuzzy set A, ·A…ui† indicates the degree of membership of uiin the fuzzy set A, ·A…ui† 2 [0; 1], the symbol ``+ ’’ means the union operator, the symbol ``/’’ represents the separator, and 1 µ i µ n.
De® nition 2.1. Let A and B be two fuzzy sets of the universe of discourse U with membership functions ·Aand ·B, respectively. The union of the fuzzy sets A and B is de® ned by
·A [ B…u† ˆ max{uA…u†; ·B…u†}; 8u 2 U: …2† The intersection of A and B, denoted as A \ B, is de® ned by
·A \ B…u† ˆ min{·A…u†; ·B…u†}; 8u 2 U: …3† The complement of A, denoted as AA, is de® ned by
·AA…u† ˆ 1 ¡ ·A…u†; 8u 2 U: …4†
De® nition 2.2. Let A and B be two fuzzy sets de® ned on the universe of
discourse U with membership functions ·A and ·B, respectively. The fuzzy subsethood S…A;B† (Kosko, 1986; Yuan & Shaw, 1995) measures the degree in which A is a subset of B:
S…A;B† ˆM…A \ B†M…A† ˆ X u 2 U
Min…·A…u†; ·B…u†† X
u 2 U
·A…u† ; …5† where S…A;B† 2 [0;1].
A New Method for Generating Fuzzy Rules 647
A REVIEW OF YUAN AND SHAW’S METHOD FOR FUZZY RULES GENERATION
In the following, we brie¯ y review Yuan and Shaw’s method for fuzzy rules generation (1995). In a fuzzy classi® cation problem, a collection of cases
U ˆ {u} is represented by a set of attributes A ˆ {A1; . . . ;Ak}, where U is called the object space (Yuan & Shaw, 1995). Each attribute Akdepicts some important feature of a case and is usually limited to a small set of discrete linguistic terms T …Ak† ˆ {T1k; . . . ;Tskk}. In other words, T …Ak) is the domain
of the attribute Ak. Each case u in U is classi® ed into a class Ci, where Ci is a member of classes C and C ˆ {C1; . . . ;CL}. In our discussions, both cases and classes are fuzzy. The class Ciof C, i ˆ 1;. . . ;L , is a fuzzy set de® ned on the universe of cases U. The membership function ·ci…u† assigns a degree to
which u belongs to class Ci. The attribute Akis a linguistic variable that takes linguistic values from T …Ak† ˆ {T1k; . . . ;Tskk}. The linguistic values T
k j are also fuzzy sets de® ned on U. The membership value ·Tk
j…u† depicts the degree
to which case u’s attribute Akis Tk
j. A fuzzy classi® cation rule (or abbreviated into fuzzy rule) can be written in the form
IF …A1is T1i1† AND . . . AND …Ak is T
k
ik† THEN …C is Cj†: …6†
Using a machine-learning method from a training set of cases whose class is known can induce a set of classi® cation rules. An example of a small training data set of the Saturday Morning Problem (Yuan & Shaw, 1995) with fuzzy membership values is shown in Table 1. In the Saturday Morning Problem, a case is a Saturday morning’s weather which can have four attri-butes:
Attribute ˆ {Outlook, Temperature, Humidity, Wind}, and each attribute has linguistic values
Outlook ˆ {Sunny, Cloudy, Rain}, Temperature ˆ {Hot, Mild, Cool}, Humidity ˆ {Humid, Normal}, Wind ˆ {Windy, Not windy}.
The classi® cation result (i.e., Plan) is the sport to be taken on that weekend day, Plan ˆ {Volleyball, Swimming, Weightlifting}.
The fuzzy decision tree induction method presented in Yuan and Shaw (1995) consists of the following steps:
T A B L E 1 A Sm al l D at a Se t fo r th e Sa tu rd ay M or ni ng P ro bl em (Y ua n & Sh aw , 19 95 ) O ut lo ok T em pe ra tu re H um id it y W in d P la n C as e Su nn y C lo ud y R ai n H ot M ild C oo l H um id N or m al W in dy N ot -w in dy V ol le yb al l Sw im m in g W -l if ti ng 1 0. 9 0. 1 0 1 0 0 0. 8 0. 2 0. 4 0. 6 0 0. 8 0. 2 2 0. 8 0. 2 0 0. 6 0. 4 0 0 1 0 1 1 0. 7 0 3 0 0. 7 0. 3 0. 8 0. 2 0 0. 1 0. 9 0. 2 0. 8 0. 3 0. 6 0. 1 4 0. 2 0. 7 0. 1 0. 3 0. 7 0 0. 2 0. 8 0. 3 0. 7 0. 9 0. 1 0 5 0 0. 1 0. 9 0. 7 0. 3 0 0. 5 0. 5 0. 5 0. 5 0 0 1 6 0 0. 7 0. 3 0 0. 3 0. 7 0. 7 0. 3 0. 4 0. 6 0. 2 0 0. 8 7 0 0. 3 0. 7 0 0 1 0 1 0. 1 0. 9 0 0 1 8 0 1 0 0 0. 2 0. 8 0. 2 0. 8 0 1 0. 7 0 0. 3 9 1 0 0 1 0 0 0. 6 0. 4 0. 7 0. 3 0. 2 0. 8 0 10 0. 9 0. 1 0 0 0. 3 0. 7 0 1 0. 9 0. 1 0 0. 3 0. 7 11 0. 7 0. 3 0 1 0 0 1 0 0. 2 0. 8 0. 4 0. 7 0 12 0. 2 0. 6 0. 2 0 1 0 0. 3 0. 7 0. 3 0. 7 0. 7 0. 2 0. 1 13 0. 9 0. 1 0 0. 2 0. 8 0 0. 1 0. 9 1 0 0 0 1 14 0 0. 9 0. 1 0 0. 9 0. 1 0. 1 0. 9 0. 7 0. 3 0 0 1 15 0 0 1 0 0 1 1 0 0. 8 0. 2 0 0 1 16 1 0 0 0. 5 0. 5 0 0 1 0 1 0. 8 0. 6 0 649
1. fuzzi® cation of the training data, 2. induction of a fuzzy decision tree,
3. conversion of the decision tree into a set of rules, 4. application of the fuzzy rules for classi® cation.
Using the data shown in Table 1, the generated fuzzy decision tree is shown in Figure 1. From the fuzzy decision tree shown in Figure 1, we can enumerate the number of routes from root to leaf. Each route can be con-verted into a rule, where the condition part represents the attributes on the passing branches from the root to the leaf and the conclusion part represents
FIGURE 1. The induced fuzzy decision tree and fuzzy rules of Yuan and Shaw’s method (1995) .
the class at the leaf with the highest classi® cation truth level. The generated fuzzy rules after conversion from the fuzzy decision tree are also shown in Figure 1. Yuan and Shaw (1995) pointed out that Rule 3: ``IF T emperature is
Hot AND Outlook is Rain THEN W eightlifting’’ can be simpli® ed into Rule
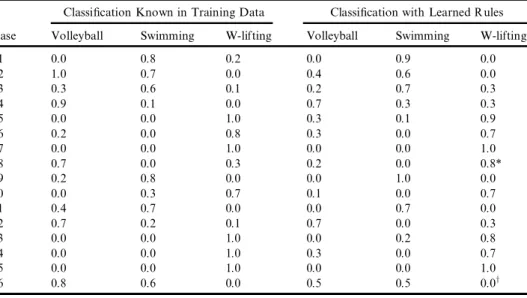
3¢: ``IF Outlook is Rain THEN W eightlifting.’’ The truth level of Rule 3¢ is 0.89 and is not less than 0.73 (the truth level of the original Rule 3). With the generated six fuzzy rules in Figure 1, the classi® cation results for the training data shown in Table 1 are shown in Table 2. Among 16 training cases, 13 cases (except cases 2, 8, 16) are correctly classi® ed. The classi® cation accuracy of Yuan and Shaw’s method is13
16£ 100% ˆ 81%.
A NEW METHOD FOR GENERATING FUZZY RULES FROM NUMERICAL DATA
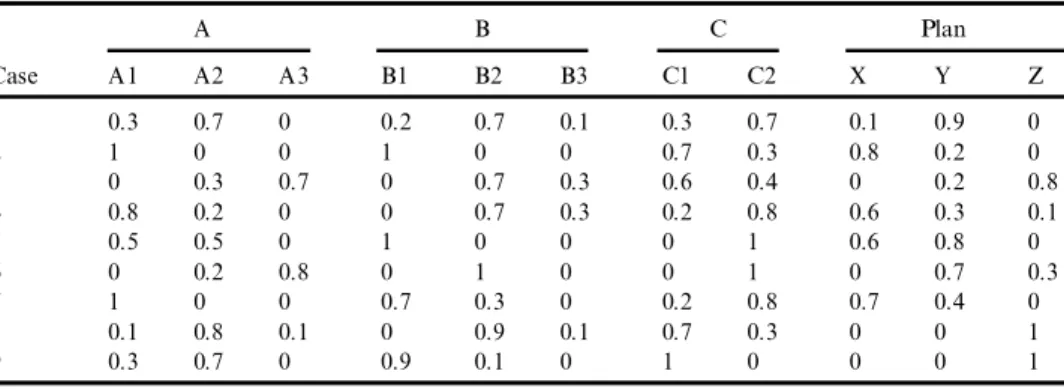
In the following, we present a new method for generating fuzzy rules from numerical data. The data set we use to introduce the concepts of fuzzy rules generation is shown in Table 3. In Table 3, we have nine cases with three attributes for each case and three kinds of decisions for each plan:
Attribute= {A, B, C}
A New Method for Generating Fuzzy Rules 651
TABLE 2 Learning Result from the Small Training Data Set (Yuan & Shaw, 1995)
Classi® cation Known in Training Data Classi® cation with Learned Rules Case Volleyball Swimming W-lifting Volleyball Swimming W-lifting
1 0.0 0.8 0.2 0.0 0.9 0.0 2 1.0 0.7 0.0 0.4 0.6 0.0 3 0.3 0.6 0.1 0.2 0.7 0.3 4 0.9 0.1 0.0 0.7 0.3 0.3 5 0.0 0.0 1.0 0.3 0.1 0.9 6 0.2 0.0 0.8 0.3 0.0 0.7 7 0.0 0.0 1.0 0.0 0.0 1.0 8 0.7 0.0 0.3 0.2 0.0 0.8* 9 0.2 0.8 0.0 0.0 1.0 0.0 10 0.0 0.3 0.7 0.1 0.0 0.7 11 0.4 0.7 0.0 0.0 0.7 0.0 12 0.7 0.2 0.1 0.7 0.0 0.3 13 0.0 0.0 1.0 0.0 0.2 0.8 14 0.0 0.0 1.0 0.3 0.0 0.7 15 0.0 0.0 1.0 0.0 0.0 1.0 16 0.8 0.6 0.0 0.5 0.5 0.0y
* Wrong classi® cation
yCannot distinguish between two or more classes.
and each attribute has linguistic terms A ˆ {A1, A2, A3}
B ˆ {B1, B2, B3} C ˆ {C1, C2}.
The classi® cation is the decision to be made on a case with attributes Ai, Bj, and Ck, respectively, to carry out one of the plans X, Y, or Z:
Plan ˆ {X,Y,Z}.
We want to generate fuzzy classi® cation rules from the given numerical data in Table 3. The generated fuzzy classi® cation rules are in the form of formula (6). For example,
Rule 1: IF A is A1 THEN Plan is X,
Rule 2: IF B isNOT B3 AND C is C2 THEN Plan is Y,
Rule 3: IF MF(Rule 1)< AND MF(Rule 2)< THEN Plan is Z,
are the rules that satis® ed our purpose, where MF means ``membership function value’’ (Yuan & Shaw, 1995), is an applicability threshold value, and 2 [0;1].
All the attributes and classi® cations are vague by nature, since they represent a human’s cognition and desire. For example, peoples’ feeling of cool, mild, and hot are vague and there are no de® nite boundaries between them. Assume that attributes ``A,’’ ``B,’’ and ``C’’ stand for some attributes of weather, respectively, and assume that ``X,’’ ``Y,’’ and ``Z’’ stand for sport plans of ``volleyball,’’ ``Swimming,’’ and ``Weightlifting’’ for a special day, respectively. Although there are distinctions between the sport plans such as ``Swimming’’ or ``Volleyball,’’ the classi® cation when it is interpreted as the
TABLE 3 A Small Data Set for Illustrating the Proposed Fuzzy Rules Generation Method
A B C Plan Case A1 A2 A3 B1 B2 B3 C1 C2 X Y Z 1 0.3 0.7 0 0.2 0.7 0.1 0.3 0.7 0.1 0.9 0 2 1 0 0 1 0 0 0.7 0.3 0.8 0.2 0 3 0 0.3 0.7 0 0.7 0.3 0.6 0.4 0 0.2 0.8 4 0.8 0.2 0 0 0.7 0.3 0.2 0.8 0.6 0.3 0.1 5 0.5 0.5 0 1 0 0 0 1 0.6 0.8 0 6 0 0.2 0.8 0 1 0 0 1 0 0.7 0.3 7 1 0 0 0.7 0.3 0 0.2 0.8 0.7 0.4 0 8 0.1 0.8 0.1 0 0.9 0.1 0.7 0.3 0 0 1 9 0.3 0.7 0 0.9 0.1 0 1 0 0 0 1
desire to play can still be vague. For example, the weather can be excellent or just okay for swimming. The classi® cation has the same situation. For example, the weather could be suitable for both swimming and playing volleyball and one may feel that it is di cult to select between the two.
As shown in Table 3, we have nine cases, where each case has three attributes to describe it. For each attribute, we have two or three terms to choose. In addition to the attribute part, we have to decide on a plan. One of decisions ``X,’’ ``Y,’’ or ``Z’’ is the plan to be decided for a speci® c case. The value accompanying each term or decision of plan is in the range [0, 1]. For each case, we can decide which decision of plan (with the highest possibility value) is most likely to be chosen. For example, in Case 6, the possibility to choose decision ``X’’ is 0, to choose decision ``Y’’ is 0.7, to choose decision ``Z’’ is 0.3, and the ® nal decision is plan ``Y.’’
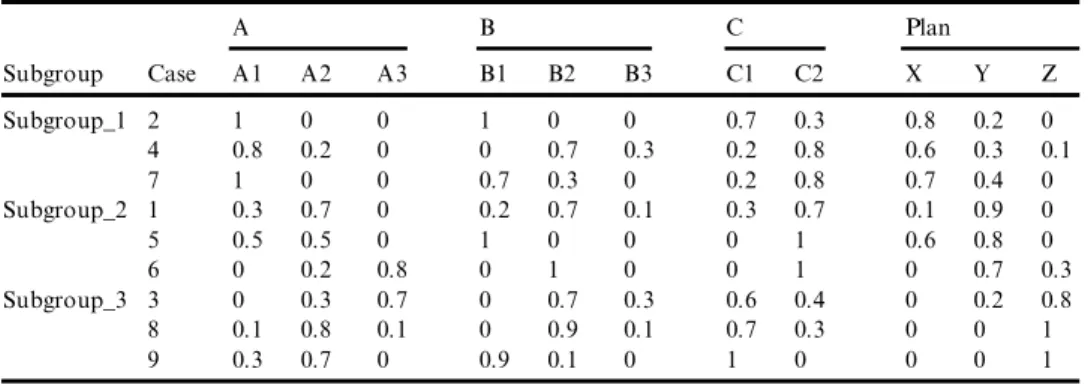
From the possibility values of decisions ``X,’’ ``Y,’’ and ``Z,’’ for each case, we can decide which decision to make for a speci® c case. If we divide the nine cases into three subgroups according to the classi® cation results, i.e., ``X,’’ ``Y,’’ and ``Z,’’ we can get another table as shown in Table 4. As Table 4 depicts, there are three instances for ``X,’’ three instances for ``Y,’’ and three instances for ``Z,’’ respectively. After carefully examining the table, it seems that there are close relationships between classi® cation results (decision of plan for that subgroup) and some terms of the attributes. Making use of the fuzzy subsethood concept (Kosko, 1986; Yuan & Shaw, 1995), we can get information about the relationship between the decision of the plan and every distinct term of the attributes.
In each subgroup, we calculate the fuzzy subsethood values between decisions of that subgroup and every term of each attribute. After the com-putations of subsethood values, we can get a set of subsethood values for each decision. In this set of values, the larger the value, the closer the rela-tionship between the decision of the plan and the term. For each subgroup, we can attain the most important factors that result in the decision of the
A New Method for Generating Fuzzy Rules 653
TABLE 4 Three Subgroups According to the Decision to be Made
A B C Plan Subgroup Case A1 A2 A3 B1 B2 B3 C1 C2 X Y Z Subgroup_1 2 1 0 0 1 0 0 0.7 0.3 0.8 0.2 0 4 0.8 0.2 0 0 0.7 0.3 0.2 0.8 0.6 0.3 0.1 7 1 0 0 0.7 0.3 0 0.2 0.8 0.7 0.4 0 Subgroup_2 1 0.3 0.7 0 0.2 0.7 0.1 0.3 0.7 0.1 0.9 0 5 0.5 0.5 0 1 0 0 0 1 0.6 0.8 0 6 0 0.2 0.8 0 1 0 0 1 0 0.7 0.3 Subgroup_3 3 0 0.3 0.7 0 0.7 0.3 0.6 0.4 0 0.2 0.8 8 0.1 0.8 0.1 0 0.9 0.1 0.7 0.3 0 0 1 9 0.3 0.7 0 0.9 0.1 0 1 0 0 0 1
plan of that subgroup. We can use these terms to form the condition part of the classi® cation rule for that decision of the plan. The consequent part of the rule is the decision of the plan for that subgroup.
From Table 4, we can see that there are three subgroups of cases. In each subgroup, the decision to be made is ® xed. To ® nd the closeness between the decision and each term of the three attributes, we ® rst calculate the subset-hood values for them. The meaning of fuzzy subsetsubset-hood value is de® ned by using formula (5), A is a subset of B, de® ned by
S…A;B† ˆM…A \ B†M…A† :
Take Subgroup_1 as an example (``X’’ is the decision of Subgroup_1), the denominator and the numerator of the subsethood formula for S(X, Al) are as follows:
M…X† ˆ 0:8 ‡ 0:6 ‡ 0:7 ˆ 2:1;
M…X \ A1† ˆ Min…0:8;1† ‡ Min…0:6;0:8† ‡ Min…0:7;1† ˆ 0:8 ‡ 0:6 ‡ 0:7
ˆ 2:1: The value of S(X, A1) is
S…X;A1† ˆ M…X \ A1†=M…X† ˆ 2:1=2:1
ˆ 1;
where S…X;A1† stands for the subsethood of ``X’’ to ``A1’’ of ``A’’ in Subgroup_1.
Using the same formula (i.e., formula (5)), we can compute all the subset-hood values as summarized in Figure 2. From Figure 2, we can ® nd that some terms are closely related to the decision to be made in that subgroup and some are not. We need a standard to distinguish close or not close enough between the decision and terms of attributes. We use the level threshold value ¬ as the standard to measure close enough or not on fuzzy subsethood values between the decision of the subgroup and all terms of attributes, where ¬ 2 [0;1]. Assume that the value we assigned to the level threshold ¬ is 0.9. For each attribute, we can select at most one term. If there are two or more terms belonging to the same attribute which have a fuzzy subsethood value not less than 0.9, the one with the largest fuzzy subsethood value will be chosen. If there
are two terms with subsethood values not less than 0.9 at the same time, the term which is the original term of the attribute will have privilege over the one which is a complemented term of the same attribute.
Referring to Figure 2 the fuzzy subsethood values (including those for the complement terms) not less than the level threshold value ¬, where ¬ ˆ 0:9, in Subgroup_1 are S(X, A1) = 1, S(X, NOT A2) = 0.9, and S(X, NOT A3) = 1. Because ``A1,’’ ``A2,’’ and ``A3’ ’ are all terms of attribute ``A,’’ only one of them will be chosen. In this condition, ``A1’’ is the only original term that belongs to attribute ``A,’’ and it is the one we choose among them. From this term we can generate the ® rst fuzzy rule as follows:
Rule 1: IF A is A1 THEN Plan is X:
Likewise, the fuzzy subsethood values that are not less than 0.9 in Subgroup_2 are S(Y, NOT B3)= 0.96 and S(Y, C2)= 0.92. The generated fuzzy rule is as follows:
Rule 2: IF B is NOT B3 AND C is C2 THEN Plan is Y:
For a rule to be generated, there must be at least one original term not less than ¬. From Subgroup_3, we can see that the subsethood values are quite average. In this condition, no term is outstanding among them (no term has a value not less than 0.9 in Subgroup_3). This means that for decision ``Z,’’ those terms of attributes are average and no terms are representative enough. Thus, Rule 3 is unable to be generated at this time.
We use MF(Rule i)= MF(condition part of Rule i), where 1 µ i µ 2 and MF means ``membership function value’’ (Yuan & Shaw, 1995). If we want
A New Method for Generating Fuzzy Rules 655 Subgroup_1(X):
Subgroup_2(Y):
Subgroup_3(Z):
FIGURE 2. The list of the fuzzy subsethood values for small data set.
to classify Case 3 of Table 3, then we can get MF…condition part of Rule 1†ˆMF…A1† ˆ 0;
MF…condition part of Rule 2†ˆMF…NOT B3 \ C2†ˆ …1 ¡ 0:3† \ 0:4 ˆ 0:4; MF…Rule 1† ˆ MF…condition part of Rule 1† ˆ 0;
MF…Rule 2† ˆ MF…condition part of Rule 2† ˆ 0:4:
Because both membership values of the existing rules are not high enough to choose decision ``X’’ or decision ``Y,’’ it is very possible that decision ``Z’’ is more appropriate than the other two decisions. In this situation, we need another applicability threshold value , where 2 [0;1], to judge the applic-ability of the existing rules. The existing rules are applicable to a case if MF(Rule i) ¶ , where i 2 {1;. . . ;n} and n is the number of existing rules.
As an alternative, we can conclude that a case that is not well classi® ed by Rule 1 and Rule 2 will be classi® ed into the plan with decision ``Z.’’ Thus, the third fuzzy rule is generated as follows:
Rule 3: IF MF…Rule 1† < AND MF…Rule 2† < THEN Plan is Z;
where MF(Rule i)= MF(condition part of Rule i), where 1 µ i µ 2 and MF means ``membership function value’’ (Yuan & Shaw, 1995), and is an applicability threshold value that MF(Rule 1) or MF(Rule 2) must exceed if that rule is applicable to a case, where 2 [0;1].
To apply the generated fuzzy rules to each case of the data sets shown in Table 3, we must assign the applicability threshold value in advance, where 2 [0;1]. For each case, calculate MF(Condition part of Rule 1) and MF(Condition part of Rule 2), respectively, and then assign MF(Rule 1) ˆ MF(Condition part of Rule 1), MF(Rule 2) ˆ MF(Condition part of Rule 2). The applicability threshold value is used to compare MF(Rule 1) and MF(Rule 2), respectively, for the speci® ed case. If both MF(Rule 1) and MF(Rule 2) are less than , then we let MF(Rule 3)ˆ1. Otherwise, we let MF(Rule 3) ˆ 0.
In the example of Table 3, the classi® cation results of Rule 1, Rule 2, and Rule 3 are ``X,’’ ``Y,’’ and ``Z,’’ respectively. The possibility values of the classi® cation result for a speci® c case with respect to ``X,’’ ``Y,’’ and ``Z’’ are represented by ``Plan(X),’’ ``Plan(Y),’’ and ``Plan(Z)’’ for a speci® c case, we can assign
Plan…X† ˆ MF…Rule 1†;
Plan…Y† ˆ MF…Rule 2†; …7† Plan…Z† ˆ MF…Rule 3†:
The generated fuzzy rules at the level threshold value ¬ ˆ 0:9 are listed as follows:
Rule 1: F A is Al THEN Plan is X:
Rule 2: IF B is NOT B3 AND C is C2 THEN Plan is Y:
Rule 3: IF MF…Rule 1† < AND MF…Rule 2† < THEN Plan is Z:
Assume that the applicability threshold value in the explained example is 0.6 (i.e., ˆ 0:6), then
1. From Case 1 of Table 3, we can get
MF…condition part of Rule 1† ˆ MF…A is Al† ˆ 0:3;
MF…condition part of Rule 2† ˆ MF…B is NOT B3 AND C is C2† ˆ MF…B is NOT B3 \ C is not C2† ˆ MF…B is NOT B3† \ MF…C is C2† ˆ Min{…l ¡ 0:l†; 0:7}
ˆ 0:7;
MF…Rule 1† ˆ MF…condition part of Rule 1† ˆ 0:3; MF…Rule 2† ˆ MF…condition part of Rule 2† ˆ 0:7:
Because MF(Rule 1) < and MF(Rule 2)> , where ˆ 0:6, thus MF(Rule 3) ˆ 0.
From formula (7), the possibility values of the decisions of plan for Case 1 are
Plan…X† ˆ MF…Rule 1† ˆ 0:3; Plan…Y† ˆ MF…Rule 2† ˆ 0:7; Plan…Z† ˆ MF…Rulea3† ˆ 0;
and we ® ll Plan(X), Plan(Y), and Plan(Z) (i.e., 0.3, 0.7, and 0) into the last three columns of Case 1 in Table 5. Because Plan(Y) is the one with the highest possibility value among the values of Plan(X), Plan(Y), and Plan(Z), the decision to be made for Case 1 is ``Y.’’
A New Method for Generating Fuzzy Rules 657
2. From Case 2 of Table 3, we can get
MF…condition part of Rule 1† ˆ MF…A is Al† ˆ 1;
MF…condition part of Rule 2† ˆ MF…B is NOT B3 AND C is C2† ˆ MF…B is NOT B3 \ C is C2† ˆ MF…B is NOT B3† \ MF…C is C2† ˆ Min{…l ¡ 0†; 0:3} ˆ 0:3;
MF…Rule 1† ˆ MF…condition part of Rule 1† ˆ 1; MF…Rule 2† ˆ MF…condition part of Rule 2† ˆ 0:3:
Because MF(Rule 1) > and MF(Rule 2) < , where ˆ 0:6, thus MF(Rule 3) = 0.
From formula (7), the possibility values of the decisions of plan for Case 2 are
Plan…X† ˆ MF…Rule1† ˆ 1; Plan…Y† ˆ MF…Rule 2† ˆ 0:3;
Plan…Z† ˆ MF…Rule3† ˆ 0;
and we ® ll Plan(X), Plan(Y), and Plan(Z) (i.e., 1, 0.3, and 0) into the last three columns of Case 2 in Table 5. Because Plan(X) is the one with the highest possibility value among the values of Plan(X), Plan(Y), and Plan(Z), the decision to be made for Case 2 is ``X.’’
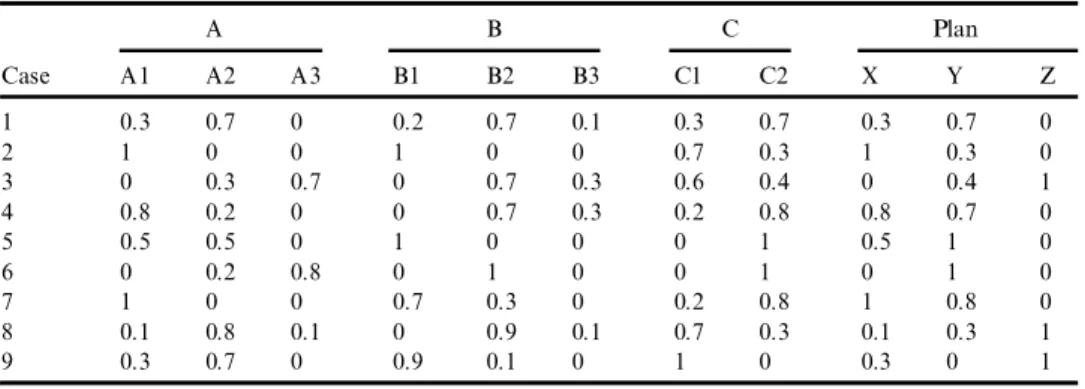
TABLE 5 Results After Applying the Generated Fuzzy Rules to Table 3
A B C Plan Case A1 A2 A3 B1 B2 B3 C1 C2 X Y Z 1 0.3 0.7 0 0.2 0.7 0.1 0.3 0.7 0.3 0.7 0 2 1 0 0 1 0 0 0.7 0.3 1 0.3 0 3 0 0.3 0.7 0 0.7 0.3 0.6 0.4 0 0.4 1 4 0.8 0.2 0 0 0.7 0.3 0.2 0.8 0.8 0.7 0 5 0.5 0.5 0 1 0 0 0 1 0.5 1 0 6 0 0.2 0.8 0 1 0 0 1 0 1 0 7 1 0 0 0.7 0.3 0 0.2 0.8 1 0.8 0 8 0.1 0.8 0.1 0 0.9 0.1 0.7 0.3 0.1 0.3 1 9 0.3 0.7 0 0.9 0.1 0 1 0 0.3 0 1
3. From Case 3 of Table 3, we can get
MF…condition part of Rule 1† ˆ MF…A is Al† ˆ 0;
MF…condition part of Rule 2† ˆ MF…B is NOT B3 AND C is C2† ˆ MF…B is NOT B3 \ C is C2† ˆ MF…B is NOT B3 \ MF…C is C2† ˆ Min{…l ¡ 0:3†; 0:4}
ˆ 0:4;
MF…Rule 1† ˆ MF…condition part of Rule 1† ˆ 0; MF…Rule 2† ˆ MF…condition part of Rule 2† ˆ 0:4:
Because MF(Rule 1) < and MF(Rule 2) < , where ˆ 0:6, thus MF(Rule 3) = 1.
From equation (7), the possibility values of the decisions of plan for Case 3 are
Plan…X† ˆ MF…Rule1† ˆ 0; Plan…Y† ˆ MF…Rule2† ˆ 0:4;
Plan…Z† ˆ MF…Rule3† ˆ 1;
and we ® ll Plan(X), Plan(Y), and Plan(Z) (i.e., 0, 0.4, and 1) into the last three columns of Case 3 in Table 5. Because Plan(Z) is the one with the highest possibility value among the values of Plan(X), Plan(Y), and Plan(Z), the decision to be made for Case 3 is ``Z.’’
The other cases are treated in a similar way. We summarize the result in Table 5.
Based on the generated fuzzy classi® cation rules, the classi® cation results for the training data in Table 3 are shown in Table 5. Among nine training cases, all cases are correctly classi® ed. The classi® cation accuracy rate is 100%.
EXPERIMENT RESULTS
In the following, we use an example (Yuan & Shaw, 1995) (i.e., the Saturday Morning Problem) to illustrate the fuzzy rules generation process.
Example. Assume that the small data set we use here is the same as Yuan
and Shaw (1995) and shown in Table 1. From Table 1, we can see that there
A New Method for Generating Fuzzy Rules 659
are four attributes for each case and there are three kinds of sport for each plan:
Attribute ˆ {Outlook, Temperature, Humidity, Wind), and each attribute has terms shown as follows:
Outlook {Sunny, Cloudy, Rain), Temperature ˆ {Hot, Cool, Mild), Humidity ˆ {Humid, Normal), Wind ˆ {Windy, Not-windy).
The classi® cation result is the sport plan to be played on the weekend day: Plan ˆ {Volleyball, Swimming, Weightlifting}.
Assume that the values for level threshold value ¬ and applicability threshold value are 0.9 and 0.6, respectively (i.e., ¬ ˆ 0:9 and ˆ 0:6). From Table 1, we divide the 16 cases into three subgroups according to the sport plan with the highest possibility value in each case. The result of the division is as follows (refer to Table 6):
1. Subgroup_1 with ``Volleyball’’ as the activity to be taken: Cases 2, 4, 8, 12, and 16.
2. Subgroup_2 with ``Swimming’’ as the activity to be taken: Cases 1, 3, 9, and 11.
3. Subgroup_3 with ``Weightlifting’’ as the activity to be taken: Cases 5, 6, 7, 10, 13, 14, and 15.
According to formula (5), the calculations for subsethood for all three subgroups are shown in Figure 3.
According to the previous discussions, there are three fuzzy rules to be generated for ¬ ˆ 0:9 and ˆ 0:6 which are summarized as follows:
Rule 1: IF Outlook is NOT Rain AND Humidity is Normal AND Wind
is Not-windy
THEN Plan is Volleyball.
Rule 2: IF Outlook is NOT Rain AND Temperature is Hot
THEN Plan is Swimming.
Rule 3: IF MF(Rule 1) < AND MF(Rule 2) <
THEN Plan is Weightlifting.
T A B L E 6 T hr ee Su bg ro up s A cc or di ng to th e Sp or t to be T ak en O ut lo ok T em pe ra tu re H um id it y W in d P la n Su b-G ro up C as e Su nn y C lo ud y R ai n H ot M ild C oo l H um id N or m al W in dy N ot -w in dy V ol le yb al l Sw im m in g W -l if ti ng Su bg ro up _1 2 0. 8 0. 2 0 0. 6 0. 4 0 0 1 0 1 1 0. 7 0 4 0. 2 0. 7 0. 1 0. 3 0. 7 0 0. 2 0. 8 0. 3 0. 7 0. 9 0. 1 0 8 0 1 0 0 0. 2 0. 8 0. 2 0. 8 0 1 0. 7 0 0. 3 12 0. 2 0. 6 0. 2 0 1 0 0. 3 0. 7 0. 3 0. 7 0. 7 0. 2 0. 1 16 1 0 0 0. 5 0. 5 0 0 1 0 1 0. 8 0. 6 0 Su bg ro up _2 1 0. 9 0. 1 0 1 0 0 0. 8 0. 2 0. 4 0. 6 0 0. 8 0. 2 3 0 0. 7 0. 3 0. 8 0. 2 0 0. 1 0. 9 0. 2 0. 8 0. 3 0. 6 0. 1 9 1 0 0 1 0 0 0. 6 0. 4 0. 7 0. 3 0. 2 0. 8 0 11 0. 7 0. 3 0 1 0 0 1 0 0. 2 0. 8 0. 4 0. 7 0 Su bg ro up _3 5 0 0. 1 0. 9 0. 7 0. 3 0 0. 5 0. 5 0. 5 0. 5 0 0 1 6 0 0. 7 0. 3 0 0. 3 0. 7 0. 7 0. 3 0. 4 0. 6 0. 2 0 0. 8 7 0 0. 3 0. 7 0 0 1 0 1 0. 1 0. 9 0 0 1 10 0. 9 0. 1 0 0 0. 3 0. 7 0 1 0. 9 0. 1 0 0. 3 0. 7 13 0. 9 0. 1 0 0. 2 0. 8 0 0. 1 0. 9 1 0 0 0 1 14 0 0. 9 0. 1 0 0. 9 0. 1 0. 1 0. 9 0. 7 0. 3 0 0 1 15 0 0 1 0 0 1 1 0 0. 8 0. 2 0 0 1 661
Subgroup_1(Volleyball):
Subgroup_2(Swimming):
Subgroup_3(Weight-lifting):
FIGURE 3. The list of the fuzzy subsethood values for the Saturday Morning Problem.
TABLE 7 Learning Result of the Saturday Morning Problem with the Generated Fuzzy Rules
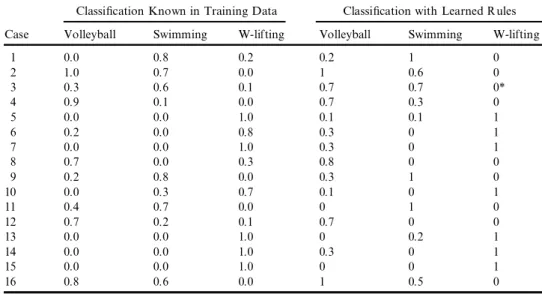
Classi® cation Known in Training Data Classi® cation with Learned Rules Case Volleyball Swimming W-lifting Volleyball Swimming W-lifting
1 0.0 0.8 0.2 0.2 1 0 2 1.0 0.7 0.0 1 0.6 0 3 0.3 0.6 0.1 0.7 0.7 0* 4 0.9 0.1 0.0 0.7 0.3 0 5 0.0 0.0 1.0 0.1 0.1 1 6 0.2 0.0 0.8 0.3 0 1 7 0.0 0.0 1.0 0.3 0 1 8 0.7 0.0 0.3 0.8 0 0 9 0.2 0.8 0.0 0.3 1 0 10 0.0 0.3 0.7 0.1 0 1 11 0.4 0.7 0.0 0 1 0 12 0.7 0.2 0.1 0.7 0 0 13 0.0 0.0 1.0 0 0.2 1 14 0.0 0.0 1.0 0.3 0 1 15 0.0 0.0 1.0 0 0 1 16 0.8 0.6 0.0 1 0.5 0
* Cannot distinguish between two or more classes.
Based on the previous discussions, we can apply the generated fuzzy rules to Table 1. The classi® cation results of the application of the generated fuzzy rules are summarized in Table 7. From Table 7, we can see that among 16 training cases, 15 cases (except Case 3) are correctly classi® ed. The classi® ca-tion accuracy rate is15
16£ 100%ˆ 93:75%.
A comparison of the number of generated fuzzy rules and accuracy rate between the proposed method and Yuan and Shaw’s method (1995) is listed in Table 8.
From Table 8, we can see that the accuracy rate of the proposed method is better than that of Yuan and Shaw’s method under ¬ ˆ 0:9 and ˆ 0:6. The number of rules generated by the proposed method is less than the number of rules generated by Yuan and Shaw’s method.
CONCLUSIONS
We have presented a new method for generating fuzzy rules from numer-ical data for handling fuzzy classi® cation problems based on the fuzzy sub-sethood values between the decisions to be made and terms of attributes of subgroups by using the level threshold value ¬ and the applicability threshold value , where ¬ 2 [0;1] and 2 [0;1]. We also apply the proposed method to deal with the Saturday Morning Problem (Yuan & Shaw, 1995). The proposed method has the following advantages:
1. The proposed method gets a better accuracy rate than the one presented in Yuan and Shaw (1995). From Table 8, we can see that the accuracy rate of the proposed method is 93.75% (for ¬ ˆ 0:9 and ˆ 0:6), while the accu-racy rate of the Yuan and Shaw’s method is 81.25%.
2. The proposed method generates fewer fuzzy rules than the one presented in Yuan and Shaw (1995). From the experimental results, we can see that the number of fuzzy rules generated by the proposed method is 3, but the number of fuzzy rules generated by Yuan and Shaw’s method is 6. 3. The proposed method needs less calculations than the one presented in
Yuan and Shaw (1995).
REFERENCES
Castro, J. L., and J. M. Zurita. 1997. An inductive learning algorithm in fuzzy systems. Fuzzy Sets and Systems 89(2):193± 203.
A New Method for Generating Fuzzy Rules 663
TABLE 8 A Comparison of the Number of Generated Fuzzy Rules and Accuracy Rate Between the Yuan
and Shaw’s (1995) Method and the Proposed Method
Yuan and Shaw’s Method (1995) The Proposed Method (for ¬ ˆ 0:9 and ˆ 0:6†
Number of rules 6 3
Accuracy rate 81.25% 93.75%
Chen, S. M., and M. S. Yeh. 1998. Generating fuzzy rules from relational database systems for estimating null values. Cybernetics and Systems: An International Journal 29(6):363± 376.
Chen, S. M., S. H. Lee, and C. H. Lee. 1999. Generating fuzzy rules from numerical data for handling fuzzy classi® cation problems. Proceedings of the 1999 National Computer Symposium, Taipei, Taiwan, Republic of China, Vol. 2, 336± 343.
Hayashi, Y., and A. Imura. 1990 Fuzzy neural expert system with automated extraction of fuzzy if-then rules from a trained neural network. Proceedings of the 1990 First International Symposium on Uncertainty Modeling and Analysis, University of Maryland, College Park, MD.
Hong, T. P., and C. Y. Lee. 1996. Induction of fuzzy rules and membership functions from training examples. Fuzzy Sets and Systems 84(1):33± 47.
Klawonn, F., and R. Kruse. 1997. Constructing a fuzzy controller from data. Fuzzy Sets and Systems 85(2):177± 193.
Kosko, B. 1986. Fuzzy entropy and conditioning. Information Sciences 40(2):165± 174.
Nozaki, K., H. Ishibuchi, and H. Tanaka. 1997. A simple but powerful heuristic method for generating fuzzy rules from numerical data. Fuzzy Sets and Systems 86(3):251± 270.
Quinlan, J. R. 1994. Decision trees and decision making. IEEE T ransactions on Systems, Man, and Cybernetics 20(2):339± 346.
Spirtes, P., C. Glymour, and R. Scheines. 1993. Causation, Prediction, and Search. New York: Springer-Verlag.
Wang, L. X., and J. M. Mendel. 1992. Generating fuzzy rules by learning from examples. IEEE Trans-actions on Systems, Man, and Cybernetics 22(6):1414± 1427.
Wu, T. P., and S. M. Chen, 1999. A new method for constructing membership functions and fuzzy rules from training examples. IEEE Transactions on Systems, Man, and Cybernetics ± Part B 29(1):25± 40. Yoshinari, Y., W. Pedrycz, and K. Hirota. 1993. Construction of fuzzy models through clustering
tech-niques. Fuzzy Sets and Systems 54(2):157± 165.
Yuan, Y., and M. J. Shaw. 1995. Induction of fuzzy decision trees. Fuzzy Sets and Systems 69(2):125± 139. Yuan, Y., and H. Zhuang. 1996. A genetic algorithm for generating fuzzy classi® cation rules. Fuzzy Sets
and Systems 84(1):1± 19.
Zadeh, L. A. 1965. Fuzzy sets. Information and Control 8:338± 353. Zadeh, L. A., 1988. Fuzzy logic. IEEE Computer 21(4):83± 91.
Zadeh, L. A. 1975. The concept of a linguistic variable and its approximate reasoning ± I. Information Sciences 8(3):199± 249.