Cavity characteristic analysis of two-dimensional phononic crystal
Jia-Yi Yeh
Department of Information Management, Chung Hwa University of Medical Technology.
E-mail : yeh@mail.hwai.edu.tw
Abstract
This paper investigated the cavity characteristics analysis of the two-dimensional phononic crystal Present phononic crystal is composed of steel cylindrical with square array embedded in air background. The plane wave expansion method and supercell calculation are adopted to obtain the band structures and transmission characteristics of the perfect and defect modes of the phononic crystal. Additionally, the COMSOL Multiphysics software is used to simulate the acoustic wave propagation in the PCs with a point defect.
Keywords: phononic crystal, point defect, cavity, supercell.
1. Introduction
In recent years, it had been attracted growing interest in the study of wave propagation in artificial periodic media because of the implications in technology and because it could be instrumental in understanding a large area of physical problems. Phononic crystals (PCs) named acoustic/sonic band gap media are the elastic analogues of photonic crystals and have also received renewed attention recently [1,2]. A phononic crystal means a number of identical structural components which are composed together to form the structure. The PCs exhibit a unique characteristic called “phononic band gaps” (PBGs) within which sound and vibrations are forbidden, and those structures exhibit unique dynamic characteristics that make them act as elastic or acoustic filters for wave propagation.
The propagation of an acoustic wave through one-dimensional PCs (or called periodic structure) had been presented by James et al. [3] and calculated the transmission coefficients of various finite structures. Then, for two-dimensional PCs, extensive work has been done on analyzing the propagation of the elastic wave. The PBGs were investigated and calculated theoretically [4] and experimentally [5] in composite systems constituted by periodic inclusions of a given material in a host matrix. The contrasts in elastic properties and densities between the constituents are emerging as critical parameters in determining the existence of PBGs and their width about 2-D and 3-D composites. Sigalas et al. [6] obtained the defect modes in two-dimensional PCs. Additionally, surface waves and localization phenomena in linear and point defect were investigated by Torres et al. [7]. Point defect characteristics of acoustic waves in square arrays of water rods in a mercury host were studied by Wu et al. [8].
Several theoretical methods have been used to study the dynamics for wave propagation in PCs, such as, the plane-wave expansion (PWE) method, the finite difference time domain (FDTD) method and the multiple- scattering theory (MST). Among these methods, the PWE method is most extensively used to calculate band structure because of its convenience. The PWE method was adopted to investigate the characteristics of the periodic system by Kushwaha et al. [9]. The finite difference time domain method was presented to study the ©2007 National Kaohsiung University of Applied Sciences, ISSN 1813-3851
wave propagation problems of the PCs by Tanaka, Tamura [10] and Garcia-Pablo [11]. Kafesaki, Economou [12] and Lai [13] studied the wave propagation problems by multiple scattering theory.
In this paper, the properties of the PCs are studied and the defect bands, band structures are also determined. The calculation is based on the plane wave expansion method and the defect mode is obtained by supercell calculation. This work investigates the acoustic wave in point defects of two-dimensional PCs which are composed of steel cylinders with square arrays embedded in air background. A defect is introduced by removing one cylinder from the middle of the PCs and the point defect can act as the resonant cavity and by using commercial software, COMSOL Multiphysics [14], the pressure in the cavity was calculated in this study.
2. Analytical Model and Calculation Method
In this paper, the band structure of the two-dimensional periodic PCs with point defect is studied. The justification is that this seems to be the only case in which the wave equation for inhomogeneous solids greatly simplifies. The wave equation of the PCs is known to be:
) ( ) ( 2 1 2 1 11 P P ∇ ⋅ ∇ = ∂ ∂ − − ρ t C , (1)
where ρ is the mass density, is the longitudinal elastic constant, is the longitudinal speed of acoustic wave, is the pressure, and is the two-dimensional nabla. Making use of the periodicity of the PCs system, the quantities and can be expanded in the two-dimensional Fourier series as the following equations: 2 11 cl C =ρ
c
l P ∇ ) ( 1 r − ρ C11−1(r)∑
⋅ − = G r iG e r) ( ) ( 1 ρ G ρ , (2)∑
⋅ − = G r iG e r C111( ) τ(G) , (3)where G is the two-dimensional reciprocal-lattice vector.
As shown in Fig. 1, the supercell with 5x5 circular cylinders (material A, steel) embedded in a background medium (material B, air), and introduces a defect by removing a central cylinder, to form two dimensional lattices with lattice spacing
a
0. The corresponding densities of the system are ρ and A ρ , respectively. Then, the BFourier coefficient can be written as follows [15]:
⎪⎩ ⎪ ⎨ ⎧ ≠ Δ ≡ ⎭⎬ ⎫ ⎩⎨ ⎧ − × − = ≡ − − + − = − − = ⋅ − − = × ⋅ − − − − − −
∑
∑
) ( ) ( ), for 0 ( ) ( ) ( 0 for , ] ) 1 ( 1 [ ) 1 ( ) ( 1 1 [( , ) ] (0,0) 1 1 1 2 1 2 1 2 2 1 G G G G G G G F e e F f N f N N N m i N N m a m m i B A B A ρ ρ ρ ρ ρ ρ ρ (4) in which, 2 0 2 2 0 a N rf =π is the filling fraction of one cylinder in the supercell and F(G) is the structure factor. An equation analogous to Eq.(4) can be written for τ(G) in terms of 111. For the cylinder with radius in
−
present system, the structure factor F(G) can be written as follows: 0 0 1( ) 2 ) ( r r J f F G G G = , (5)
where J1 is the Bessel function of the first kind of order 1.
Fig.1. The 5x5 supercell with a cavity (point defect).
Then, the eigenvalue equation can be obtained as the following form by applying the Bloch theorem:
∑
≠ ′ − − − − + − ′ + Δ + ⋅ + ′ −Δ − ′ ′ = G G k k G k G k G G G G G k ( ) ]P ( ) [ ( ) ( ) ( ) ] ( )P ( ) 0. [ρ 1 2 C111 ω2 ρ 1 C111ω2 F (6)This is a set of linear, homogeneous equations for the eigenvectors Pk(G) and eigenfrequencies ω(k) if G is permitted to take all the possible values. The Band structures of the PCs can be obtained by letting k scan the area of the irreducible region of the Brillouin zone as shown in Fig. 2.
Additionally, the COMSOL Multiphysics software is used to simulate the acoustic wave propagation in the PCs with a point defect and the equation utilized to analyze present problem and pressure fields in the cavity of the PCs is the following equation:
P P 2 2 l c ρ ω ρ = ∇ ⋅ ∇ − . (7)
3. Results and Discussions
In this study, the characteristics of point defect into the perfect PCs system consisting of steel cylinders in air background are presented. The materials properties and relative parameters are , , , and . Besides, the filling fractions of the cylinder in the unit cell,
3 / 7800kg m A = ρ 3 / 2 . 1 kg m B = ρ cA =6100m/s cB =343m/s 2 0 2 0 a r
f′=π , investigated and discussed in this paper are 0.4 (r0 a0 =0.3568), 0.5 (r0 a0 =0.4), and 0.6 (r0 a0 =0.437).
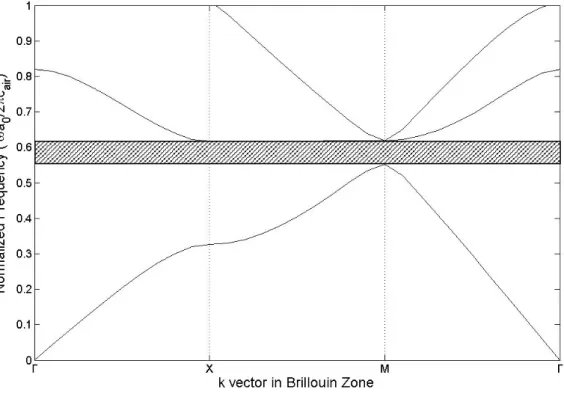
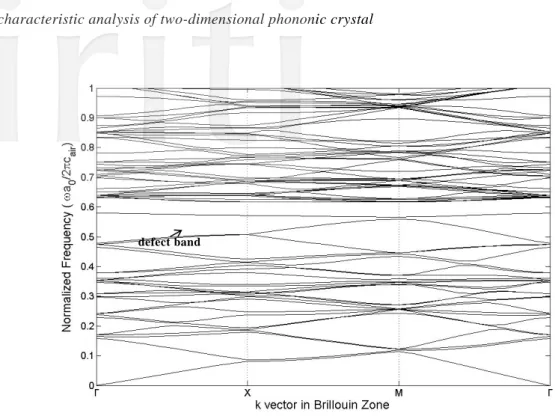
Fig. 3 (a) and (b) show the band structures with filling fraction f′=0.4 for the perfect PCs and the PCs with a point defect, respectively. In the perfect PCs, there exists a full band gaps between 5.64-6.15 kHz. And, the point defect is created by removing a single cylinder from the middle of the perfect PCs. According to the plane wave expansion method and supercell calculation, the band structure of the PCs with point defect can be obtained. The defect band of the PCs with point defect can be observed in the band gaps of the perfect PCs. The defect band can act as the pass band and the acoustic wave can pass through the PCs with a point defect at the frequency of the defect band. Besides, the frequency of the defect band is called the resonant frequency of the point defect and the acoustic will be localized in the point defect.
defect band
(b) The 5x5 supercell with pint defect.
Fig. 3. Band structure for the PCs with filling fraction f =0.4.
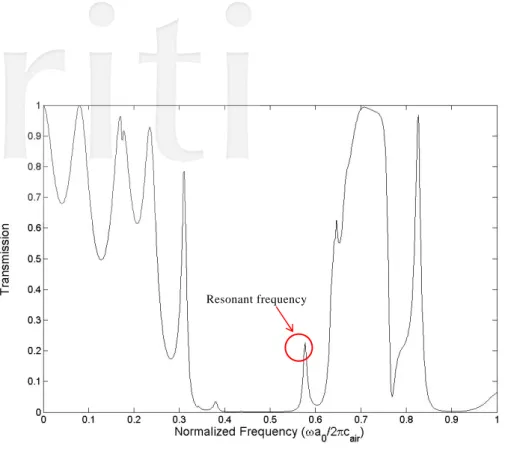
The transmission coefficients in Γ−X direction with filling fractions f =0.4 for the perfect PCs and the PCs with point defect are plotted in Fig. 4 (a) and (b), respectively. The resonant frequency of the PCs with point defect can be seen in the numerical results, and the range of the resonant frequency is about the normalized frequency 0.57-0.584. The numerical results show that we can use the acoustic propagation characteristics of the PCs with point defect to design some high-precision and high-efficacy devices according to the requirements.
Resonant frequency
(b) The 5x5 supercell with pint defect.
Fig. 4. Transmission coefficient (Γ−X direction) for the PCs with filling fraction f =0.4
Fig. 5 presents the simulated results of the pressure fields of the 5x5 PCs with a point defect with the filling fractions 0.4 The absorbing boundary conditions are used and the waves are not reflected and the acoustic waves are incident from the left-side of the PCs at a pressure of 1 Pa. According to the results, it can be seen that the incident acoustic wave will be localized in the cavity. And, it can be utilized to design some novel mechanical devices according to the difference characteristics of the pressure fields.
= f
normalized frequency=0.574
Fig. 5. Pressure field simulation of the 5x5 PCs with a cavity (point defect). ( the acoustic waves are localized in the cavity at the resonant frequency)
4. Conclusions
The acoustic characteristics of the perfect PCs and the PCs with point defect are studied in this study and the defect bands, band structures are also determined. The calculation is based on the plane wave expansion method and the defect mode is obtained by supercell calculation. From the numerical and simulated results, the following conclusions can be drawn:
The incident acoustic wave of the resonant frequency will localized in the cavity (point defect) of the PCs according to the numerical and simulated results.
The full band gaps of the perfect PCs can be controlled and also can be used to design some acoustic devices. According to the simulated results, the differences of the pressure fields for the PCs with cavity can be utilized to design some novel acoustic devices, such as high-efficacy acoustic cavity and acoustic energy generation devices.
In this study, those analytical results can be used in the development of the novel acoustic applications for the PCs with cavity.
Acknowledgements
This research was partially supported by the National Science Council in Taiwan through Grant NSC 99-2221-E-273-001-.
Reference
[1] Vasseur J.O., Djafari-Rouhani B., Dobrzynski L., Kushwaha M.S. and Halevi P., “Complete acoustic band gaps in periodic fibre reinforced composite materials: the carbon/epoxy composite and some metallic systems,“ Journal of Physics: Condensed Matter, Vol.6, pp. 8759,1994.
[2] Goffaux C. and Vigneron J.P.,” Theoretical study of a tunable phononic band gap system,” Physical Review B, Vol. 64, pp. 075118, 2001.
[3] James R., Woodley S.M., Dyer C.M. and Humphrey V.F., “Sonic bands, bandgaps, and defect states in layered structure-Theory nad experiment,” Journal of the Acoustical Society of America, Vol. 97, pp. 2041, 1995.
[4] Kushwaha M.S., Halevi P., Dobrzynski L. and Djafari-Rouhani B., “Acoustic band structure of periodic elastic composites,” Physical Review Letters, Vol. 71, pp. 2022, 1993.
[5] Montero de Espinoza F.R., Jimenez E., and Torres M., “Ultrasonic Band Gap in a Periodic Two-Dimensional Composite,” Physical Review Letters, Vol. 80, pp. 1208, 1998
[6] Sigalas M.M., “Defect states of acoustic waves in a two-dimensional lattice of solid cylinders,” Journal of Applied Physics, Vol. 84, pp. 3026, 1998
[7] Torres M., Montero de Espinosa F.R. and Aragon J.L., “Ultrasonic Wedges for Elastic Wave Bending and Splitting without Requiring a Full Band Gap,” Physical Review Letters, Vol. 86, pp. 4282, 2001
[8] Wu F., Hou Z., Liu Z. and Liu Y., “Point defect states in two-dimensional phononic crystals,” Physics Letters A, Vol. 292, pp. 198, 2001
[9] Kushwaha M. S. and Halevi P., “Giant acoustic stop bands in two-dimensional periodic arrays of liquid cylinders,” Applied Physics Letters, Vol. 69(1), pp. 31, 1996.
[10] Tanaka Y. and Tamura S.I., “Two-dimensional phononic crystals: surface acoustic waves,” Physica B, Vol. 263, pp. 77, 1999.
[11] Garcia-Pablo D., “Theory and Experiments on Elastic Band Gaps,” Physical Review Letters, Vol.84, pp. 4349, 2000. [12] Kafesaki M. and Economou E.N., “Multiple-scattering theory for three-dimensional periodic acoustic composites,”
Physical Review B, Vol.60, pp. 11993, 1999.
[13] Lai Y., Zhang X. and Zhang Z.Q., “Engineering acoustic band gaps,” Applied Physics Letters, Vol. 79, pp. 3224, 2001. [14] COMSOL 3.4a, The COMSOL Group, Stockholm, Sweden.