Training of a Neural Network Classifier by Combining Hyperplane with Exemplar Approach
Hahn-Ming Lee and Weng-Tang Wang Department of Electronic Engineering National Taiwan Institute of Technology Taipei, Taiwan. E-mail : HMLEE @ TWNNTIT.BITNET
Abstract-A neural network classifier which combines hyperplane with exemplar approach is presented. The network structure does not have to be specified before training and an appropriate network structure will be build during training.
Perceptron-based algorithm is first applied to train a linear threshold unit (LTU). The LTU will build a hyperplane that classifies as many training instances as possible. Afterwards, HB nodes that represent hyperboxes will be generated to classify the training instances that can not be classified by the hyperplane. The proposed model also works well on both clustered and strip-distributed instances. Number of HB nodes generated depends on the overlapping degree of training instances.
This classifier can classify continuous-valued and nonlinearly separable instances. In addition, on- line learning is supplied and learning speed is very fast. Furthermore, the parameters used are few and insensitive.
I. INTRODUCnON
The perceptron algorithm [l], one of the supervised learning algorithms, converges for linearly separable instances. The main drawback of the perceptron algorithm is that nonlinearly separable instances can not be classified.
Although we can build a multi-layered perceptron 121 that forms any shape of decision region to solve this problem, unfortunately, it is quite complex and has not be proven that it will converge as with single layer perceptron. Moreover, there is no existing theory for determination of network structure. According to Lippmann89 131, we know a training algorithm which can "match classifier complexity to training instances available" will obtain the best performance. In addition, hyperplane classifier [3] algorithms, such as perceptron and backpropagation, need low memory and have low computation load but training time may be long. So as to exemplar classifier 131 algorithms, they train rapidly but have high memory and computation requirements. We can see that, by combining these two approaches, the drawbacks
of each approach could be relieved. According to the above description, we want to build a hyperplane and exemplar combined classifier algorithm with appropriate network structure generation ability for classifying continuous-valued and nonlinearly separable instances.
On the other hand, taking advantage of fuzzy theory could improve the learning ability of neural networks [4]-[61.
Therefore, our proposed classifier is concemed in combining hyperplane and exemplar classifier algorithm and utilizes fuzzy theory to classify continuous-valued and nonlinearly separable instances. Besides, if instances are strip- distributed, using the exemplar classifier algorithms is not a good choice. In the proposed classifier, most of instances are classified by the hyperplane and the hyperboxes are only responsible for classification of the overlapped instances.
Therefore, number of hyperboxes needed is reduced and this makes the classifier also suitable for strip-distributed instances. The network structure of the classifier is automatically generated and the number of hidden nodes needed depends on the overlapping degree of training instances. In addition, this classifier also consists of many other features, for example, few nodes needed, on-line learning, and fast learning speed. Furthermore, the parameters needed are few and insensitive.
II. THE CLASSIFIER
This classifier is designed to generate a two-layered neural network with a single node at the output. The complete structure is illustrated in Fig.1. The first hidden layer is composed of a linear threshold unit &TU) [l] and none or some HB nodes that represent hyperboxes. HB nodes are generated for classifying those training instances that can not be correctly classified by the hyperplane (defined by the LTU node). Therefore, the number of HB nodes generated depends on the overlapping degree of training instances. The second hidden layer contains only an output node. When an input vector X is presented to the classifier, this classifier will check whether X is contained in some hyperboxes. If it is, the innermost hyperbox will send a correct classification output to the output node. Otherwise, it will be classified
0-7803-0999-5~3/$03.00 01993 IEFiE 494
1
Classification ResultInput X
Fig. 1. The stmcture of the proposed calssifier.
by the hyperplane.
A . The LTU node
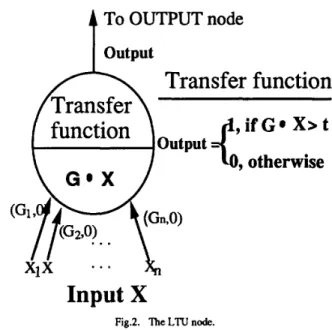
The hyperplane classifier algorithm used here is the pocket algorithm [7]. The pocket-run-length [7] was used as a stopping criterion. The LTU node shown in Fig.2 is first trained to build a hyperplane. Where Gi in Fig.2 is the only weight needed to be adjusted on ith connection. Another weight on the ith connection is zero. Since a hyperplane can be viewed as a special kind of a hyperbox, we use this formulation to make it consistent with the representation of the hyperboxes. The pocket algorithm will classify as many training instances as possible.
B. HBnodes
A fuzzy set can be viewed as a template of a class [81 with fuzzy boundary. The membership value for instances located in fuzzy boundary is less than one and greater than zero.
Boundary of kernel part of a class (instances whose membership value is equal to one) can be quickly defined by nested hyperboxes. Moreover, nested hyperboxes can be used to classify nonlinearly separable instances. Fig.3 illustrates two cases that instances can not be separated by a hyperplane.
By using two(A and B)and three(A1, A2, and B) nested
A To OUTPUT node output
Transfer function
output - , if Go X> t 0, otherwise
Input 1 X
Fig.2. "he LTU node.
Exemplars used here are hyperboxes. Each HB node represents a hyperbox. The minimun and maximun values of feature i of a hyperbox are the two weights, Li and Gi respectively, on ith connection. Since we take fuzzy set as a template of a class, using the fuzzy subsethood degree [ 131 as the membership value makes the system work well. We use Kosko's fuzzy subsethood equation [ 131 (described in Section 3) as the activation function of HB nodes. A HB node's structure and its transfer function is illustrated in fig. 4.
Simpson [9] used the same representation, but the activation function, transfer function, and the way hyperboxes used are different. The activation function used here is more neat and easily understood. When an input vector X is presented to
Fig.3. Nested hypehxes which can calssify nonlinearly separable instances.
hyperboxes respectively, instances can be easily classified.
To Output node
Y Transfer function
1, if S = 1 and (class of input X = class of the HB node = 1 )
of input X = class of the HB node = -1 ) -1, if s = 1 and (class
A Classification Result
Transfer function
output =
-1, otherwise
Input X
Fig.4. The HB node.
the proposed classifier, at most one HE3 node is allowed to be active (explained in Section 3 ).
C . The Output node
Fig.5 shows the structure and the function of the output node. All connection weights between the first hidden layer and the output node are 1. The output node receives the information from both the LTU node and the HB nodes. The activation function of the output node is weighted-Sum. If input X is contained in some hyperboxes, only the innermost hyperbox is allowed to be active (its output will be either -1 or 1). then the weighted-sum operation will correct the misclassification output coming from the LTU node.
III. LEARNING
Before detailing the learning procedure, we will explain fuzzy subsethood theorem first.
Fig.5. The Output node.
For crisp set : A c B iff b'x E A -+ x E B .
For fuzzy set : A c B iff b' X i E X , m&i) I mb(xi).
Where m,(x) and mb(x) are the membership values of element x belonging to fuzzy set A and B, respectively. The degree S(A,B) which represents the degree fuzzy set A is a subset of fuzzy set B is calculated by the equation :
S(A,B) = M ( A n B ) / M ( A ) , 0 I S(A,B) s 1 (1)
n i-1
, which M ( A ) =
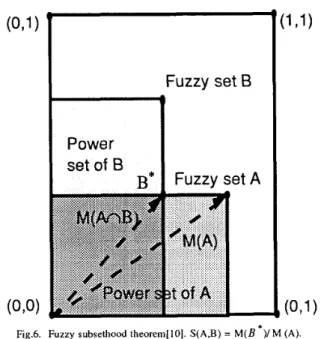
Fuzzy Set A is a subset of Fuzzy set B (S(A,B) = 1) if and only if A is within the hyperbox F ( f ) , power set of fuzzy set B. That is because M ( A n B ) = M ( A ) , and S ( A , B ) = M ( A ) / M ( A ) = 1. If fuzzy set A is outside the hyperbox F(?) as illustrated in Fig.6, then B * = A n B and.
mdxi), m- = Min(m,(X), mb(X)).
B. The learning procedure A . Fuzzy Subsethood Theorem
The membership value of a training instance belonging to a hyperbox is measured by Kosko's fuzzy subsethood equation.
The membership value of a training instance belonging to a hyperbox is measured by Kosko's fuzzy subsethood equation [ 101. It is described as follows :
Set A is a subset of set B if and only if A belongs to B's power set.
First of all, we use pocket algorithm and stopping criterion mentioned in Section 2 to build a hyperplane which classifies most of training instances. Afterwards, hyperboxes will be generated to classify the training instances that can not be classified by the hyperplane.
To avoid one feature overwhelms the others, input value for each feature must be normalized. Normalized value of each feature is between 0 and 1. The normalization equation used is :
496
S ( X , hyperbox 1') = M(WjrrZ) / M Q . (5)
n
PowerFig.6. Fuzzy subsethood theorem[lO]. S(A,B) = M(B *)/M (A).
where f),q, and f i ( m i n ) are the maximun and minimun values of feature i, respectively.
After a training instance X is normalized and presented to the proposed classifier, Kosko's fuzzy subsethood equation is used as membership function indicating the degree to which training instance X belongs to a hyperbox. Because the hyperboxes generated in the proposed classifier may be located in any position in [0,1]" instead of i n position [O.O], coordinate transformation for training instance X and each hyperbox is needed before applying Kosko's fuzzy subsethood equation. The transformation procedure is described as follows :
[Step 11 : Find the farest comer U; and nearest comer V; of each hyperbox j to the training instance X.
[Step 21 : For each hyperbox j, let W; be the coordinate of U;, and Z be the dummy coordinate of X. For each value of feature i,
W;i = I Vji - Vji I and zi = I Xi -- Uji I, (4)
The degree of a training instance belonging to a expanded hyperbox j is then calculated by the equation :
If hyperbox j is just a single point, the degree of a training instance belonging to it is calculated by the equation :
S(X,hyperbox j ) = 1 / (1 + M(Z)). (6) If training instance X is not contained in any existing hyperboxes (for each hyperbox j , S(X,Hyperbox j ) < l), the best matched hyperbox will be expanded to contain it .
The expansion criterion is : the expanded hyperbox will never overlap with other hyperboxes that represent different classes.
If expansion criterion can not be satisfied, then a new hyperbox will be generated to contain training instance X.
At this time, this new hyperbox is just a point . Because hyperboxes are only generated for training instances that can not be classified by the hyperplane, hyperboxes needed are few and the chance that cross-overlapped hyperboxes occurs is reduced. Thus, if the expansion criterion can not be satisfied, we would like to create a new hyperbox. A hyperbox is expanded by the Fuzzy-AND and Fuzzy-OR operation. That is,
L; = Fuzzy-AND(Li,xi) = Min ( L i , X i ) ,
Gi = Fuzzy-OR(G;,x;) = Max (G;,x;)
(7) (8) If the size of a hyperbox exceeds the maximun allowed size then a new hyperbox will be created. It is easy to see that, on-line learning can be supplied if we allow the hyperboxes to be expanded or generated during operation.
Fig.7 illustrates expanding situation of a hyperbox.
Because we allow hyperboxes to be nested, inner hyperboxes represent the exceptions to the surrounding hyperboxes. It may happen that a training instance X is contained in many hyperboxes (these hyperboxes is nested).
For this situation, only the innermost hyperbox will be chosen. An example is illustrates in Figure 8. In this case,
L 0
x
U XFig. 7. The hyperbox expansion
Fig. 8. The nested hyperboxes.
training instance X will be classified as the class the innermost hyperbox B represents.
IV. EXPERMENTALRESULTS
In this section, we present some experiment results produced by the simulation of proposed training algorithm.
The experiment was simulated under PDP software environmenttll] on SUN/ SPARC 11. In order to evaluate the effectiveness of the proposed model, experimental results [4 J of fuzzy perceptron and crisp perceptron running on IRIS [4] data were taken and compared to the results of the proposed model. The IRIS data set contains three classes, each with 50 instances, of four continuous features. Since only the Virginca, Versicolor of IRIS data are overlapped distributed, and Setosa is linearly separable from the above two classes, only Virginca and Versicolor were used in this experiment.
Table I summarizes the comparison results of crisp perceptron, fuzzy perceptron, and the proposed model. The data of the fmt two rows is obtained from fuzzy perceptron, and the data of the proposed model is the average of ten trials.
Pocket-run-length [7] used here is 12 and maximun allowed size of a hyperbox was set to 0.3. Inner hyperbox's size allowed was 0.25 times of outer hyperbox's. Notice that crisp perceptron is unstable because of its decision boundary deteriorates substantially as number of iteration changes.
Leaving-one-out [ 121 is another approach used here for estimating classifier error rates. Maximun allowed size of a hyperbox was set to 0.3 and the pocket-run-length was set to 12. leaving-one-out error rate of our proposed model is 0.076. It is the average of ten trials.
Fig9 shows the relationship between the maximun allowed size of a hyperbox and the number of hyperboxes generated.
We can see that the number of hyperboxes generated is not absolutely increased as the maximun allowed size of a hyper size of a hyperbox is decreased. The number of hyperboxes
generated partly depends on the input sequence of training instances and the position of generated hyperplane. Generally speaking, the higher overlapping degree of training instances is, the more hyperboxes are generated in the same condition.
Moreover, pocket-run-length and maximun size of a hyperbox allowed are the two parameters needed to be adjusted and they only affects the number of HB nodes created
It is worthwhile to notice that if instances are strip- distributed, using exemplars like hyperboxes as an approach
-
Pocket run len = 8-
Pocket run len = 12 Pocket run len = 16I .
Number of HB node
'I I , . I
c - -I- 4-\
I I 1
4.4 3.6 3.3
0.3 0.6 0.9 1.2
Maximun allowed hyperbox size
Fig 9. Relationship between hyperbox size and number of HB nodes.
498
is not a good choice. That is because number of hyperboxes needed is large and the frequency that overlapping hyperboxes occur may quite often in such situation. In our model, since most of instances are classified by a hyperplane, number of hyperboxes needed is reduced quite a lot. So, it works well on both clustered and strip-distributed instances.
V. CONCLUSION
We have proposed a neural network classifier which combines hyperplane with exemplar approach. The network structure does not have to be specified before training and the number of hidden nodes needed depends on the overlapping degree of training instances. The proposed classifier utilizes the pocket algorithm to classify most of instances. Nested hyperboxes are then generated to classify these training instances that can not be classified by the hyperplane. The hyperplane can be viewed as a special kind of a hyperbox.
Kosko's fuzzy subsethood equation is utilized as the membership function of a training instance belonging to a hyperbox. This classifier also consists of many other features, for example, it can classify continuous-valued and nonlinearly separable instances , nodes needed are quite few, on-line learning is supplied, learning parameters are few and insensitive, and its learning speed is fast. Furthermore, the proposed classifier is suitable for both clustered and strip- distributed instances.
REFERENCE
Richard P. Lippman. "An introduction to computing with neural net,"
IEEEASSP magazine. pp. 4-22, April 1987.
D. E. Rumelhart, G. E. Hinton, and R.J. Williams, "Learning
internal representations by error propagation," Parallel Distributed Processing : Explorations in the MicroBtructure of cognition, Vol. 1, Cambridge : Bradford Books / Mit press, 1986.
Richard P.Lippmann, "Pattern classification using neural networks,", IEEE Communications magazine, pp. 47-64, November 1989.
James M. Keller and Douglas J. Hunt, "Incorporating fuzzy membership function into perceptron algorithm," IEEE Transactions. on Panern Analysis and Machine Intelligence.
Vol. PAMI-7, No. 6, pp. 693699, November 1985.
Gail A. Carpenter, Stephen Grosaberg, and David B. Roren,
"Fuzzy ART : fast stable learning and categorization of analog patterns by an adaptive resonance ryatem,".Neural Networks,
W. Pedrycz, "Fuzzy logic in development of fundamentals of pattern recognition," International Journal of Approximate Reasoning. Vol. 5 , pp. 251-264. 1991.
Stephen I. Gallant, "Connectionist expert system,"
Communication. ACM, Vol. 31, No. 2, pp. 152-169, 1988.
Bezdek, J. Pattern Rrecognition with Fuzzy Objective Algorithms. Plenum Press: New York, NY, 1981.
Patric K. Simpson, "Fuzzy min-max neural networks,"
Singapore, 1991, pp. 1658-1669.
Vol. 4, pp. 759-771, 1991.
IJCNN.
[lo] Bart Kosok, Neural networh and fuzzy systems. Prentice-Hall,
[ l l ] I. McClelland and D. Rumelhard, Explorations in Parallel Distributed Processing, Cambridge : Bradford Books/Mit Press, 1988.
[12] Sholom M. Weiss and loannis Kapouleas, "An empirical comparison of pattern recognition. neural nets, and machine learning classification method," Proceeding of Eleventh International Joint Conference on Artificial Intelligence, Detroit, MI. 1989, pp. 781-787.
992.