Dynamic surfing and trapping of charged colloids in a traveling-wave
electrophoretic ratchet
Hsien-Hung Weia兲
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
and Center for Micro/Nano Science and Technology, National Cheng Kung University, Tainan 701, Taiwan 共Received 22 January 2007; accepted 23 April 2007; published online 16 May 2007兲
The author theoretically demonstrates a gel-free electrophoretic ratchet under a nearly unidirectional traveling electric field whose wavelength is much longer than the transverse dimension. Because of length scale separation, a charged particle can migrate synchronously or asynchronously with the field as if it was surfing on the wave. The author shows, with a dynamical phase portrait, that if the wave speed is slower than the characteristic electrophoretic velocity, a suspension of charged particles can be trapped into distinct particle bands synchronizing with the field. A tunable sieving capability of this ratchet provides the potential for continuous fractionation and characterization of colloidal suspensions. © 2007 American Institute of Physics. 关DOI:10.1063/1.2740176兴
Electrophoresis 共EP兲 is the motion of charged particles under the actions of an applied electric field. It has been widely used in separation of charged species and recently explored under the theme of microfluidics.1 The electro-phoretic velocity U of a charged particle in response to an electric field E is described by
U =E. 共1兲
Hereis the particle mobility of a scale/, where and
represent, respectively, dielectric constant and viscosity of the solution andis the surface zeta potential.
In this letter, we demonstrate an alternative EP scheme based on ac electric fields for separation of charged colloids. Our strategy is to utilize traveling-wave fields to produce an electrophoretic ratchet capable of trapping charged particles selectively, called traveling-wave electrophoresis 共TWEP兲. In contrast to conventional EP ratchets2,3 which often re-quires working with gel for rendering field/size dependent mobilities, a TWEP ratchet can sieve charged particles purely on a free-EP basis. The core of this ratchet invokes a length scale disparity in the field whose wavelength ᐉ is sufficiently long compared to the transverse dimension d. Because Gauss’s law with electroneutrality demands that the field must be divergence-free共it is obvious that a rigorously one-dimensional traveling field is impossible because it will inevitably lead to space charges兲, the field in the traveling direction and hence the electrophoretic velocity are much higher than those in the transverse direction. In analogy to hydrodynamic lubrication flow,4the resulting particle move-ment looks nearly unidirectional. As this character can sup-press lateral drift in a much smaller dimension, it allows the particle to move synchronously or asynchronously with the field as if it were “surfing” on the wave.5 We thus refer to such motion as a nearly one-dimensional TWEP despite its two-dimensional origin. We should also emphasize that our strategy differs fundamentally from those in previous studies5–8 using traveling-wave signals. In these early stud-ies, there involve non-equilibrium dynamics of charged toner,5,6 space charge injection,7 or high-frequency ac polarization,8 so their systems are not electro-neutral and
hence involve significant Coulombic forces. In our study, on the contrary, common colloids are typically dielectric and hence the charges are usually confined within the thin 共10–100 nm兲 Debye screening layer at Poisson-Boltzmann equilibrium. There is virtually no electrostatic attraction/ repulsion between particles even if they aggregate.9 As we shall demonstrate, our ratchet can permit non-Coulombic ag-gregation of like-charge colloids in the context of electro-phoresis; it seems unlikely to realize like-charge aggregation in these previous studies.
Let x and y stand, respectively, for the wave propagating and transverse directions with y = 0 defined at the channel bottom surface embedded with electrodes. Define the wave number k = 2/ᐉ共Ⰶ1/d兲. The longitudinal, traveling field is taken in a simple sinusoidal form satisfying Laplace equa-tion: Ex= E0cosh共k共y−d兲兲cos共k共x−ct兲兲, with the
correspond-ing transverse field Ey= E0sinh共k共y−d兲兲sin共k共x−ct兲兲 that
satisfies zero normal field penetration Ey= 0 at the top bound-ary y = d, where E0 is the characteristic field strength, c the
wave speed, and t time. Owing to much smaller transverse dimension ky⬃kdⰆ1, Ex= E0cosh共k共x−ct兲兲兲 which does
not vary in y. In addition, Eynow becomes O共E0kd兲ⰆExin magnitude and hence the velocity UyⰆUx, making trans-verse drift confined in a much smaller dimension. These two characters deduced by length scale separation stipulate that the particle motion will be dictated by the longitudinal field and hence can be viewed as nearly one dimensional. While the particle migrates in response to the traveling field, the particle position changes with time and hence the spatial influence of the field on the particle. To capture this effect, the local field E 共=Ex兲 in Eq. 共1兲 must be evaluated at the particle instant position xp共t兲, viz., x=xp共t兲⬅x0+兰0
t
U共t1兲dt1, where x0is the initial position of the particle. This yields the following equation governing the particle motion under nearly one-dimensional共1D兲 TWEP:
U =E0cos共kL兲, with L =
冕
0 tU共t1兲dt1− ct + x0. 共2兲
As a result, U is determined simultaneously by the particle displacement relative to the wave, L. L⬎0 共⬍0兲 corresponds to the particle ahead of共behind兲 the wave. As the local field a兲Electronic mail: hhwei@mail.ncku.edu.tw
APPLIED PHYSICS LETTERS 90, 204103共2007兲
0003-6951/2007/90共20兲/204103/3/$23.00 90, 204103-1 © 2007 American Institute of Physics
exerting on the particle depends on the history of the time-varying particle-field phase difference, the apparent particle mobilitycosh共kL兲 now becomes nonlinear in U. Hence the particle motion is not reversible even though is indepen-dent of the applied field—it is this irreversibility that fur-nishes the unique ratchet capable of trapping/separating charged particles, as we will show shortly.
Without loss of generality, hereinafter we consider only the motion of a positively charged共⬎0兲 particle. Letting 共X,X0兲=k共L,x0兲, V=U/U0, and= kU0t, with U0= E0
be-ing the velocity at dc fields, we rewrite Eq.共2兲in the dimen-sionless form,
X
⬘
= cos共X兲 − cˆ, with X =冕
0
V共1兲d1− cˆ+ X0, 共3兲 where cˆ = c / U0is the ratio of the wave speed to the charac-teristic electrophoretic velocity. Prime denotes the derivative with respect to . Instead of directly observing the particle trajectory in space, we adopt an alternative approach to iden-tify the nature of the particle motion. Here we employ a dynamical phase diagram10to elicit the evolution of the mo-tion in the displacement-velocity space. This approach does not require solving the solution in detail. More importantly, it can immediately reveal the stabilities of various stationary solutions共i.e., fixed points兲, so that the ultimate fate of the particle can be graphically identified without needs in carry-ing out integration or numerical simulations.
Figure 1共a兲 shows the phase diagram for Eq. 共3兲. The path of the dynamical state for X
⬘
⬎0 is toward right, whereas that for X⬘
⬍0 goes left. At X⬘
= 0, there are a num-ber of fixed points Xeat which the particle stays stationary. However, these points are not all dynamically stable,de-pending on how the two paths intercept at the X
⬘
= 0 axis. For a field with negative gradients, the fixed points toward which the two paths converge are stable; otherwise they are un-stable. Therefore, when the particle is close to the stable 共unstable兲 fixed points, it will be trapped toward 共repelled from兲 there. Since the fixed points are critical to the fate of the particle and their locations depend on cˆ, below we dis-cuss three cases:共i兲 兩cˆ兩⬍1, 共ii兲 兩cˆ兩⬎1, and 共iii兲 兩cˆ兩=1.For 兩cˆ兩⬍1 there are two fixed points within the wave-length: Xe
±
= ± cos−1共cˆ兲+2共n−1兲 共n is an integer兲. Xe +
is a stable fixed point and hence will trap the particle from any positions X苸共Xe+− 2 cos共cˆ兲,Xe+− 2 cos共cˆ兲+2兲. On the con-trary, Xe−is an unstable fixed point, so the particle near which will be repelled; yet it will take a time of at least
O共ln兩sin共Xe−兲兩兲 to be arrested again by one of the neighboring stable fixed points. In the special case of cˆ = 0, the field is stationary, so all the particles will be trapped at the zero-field points: Xe+=/ 2 + 2n, regardless of the amounts of the charges.
As for 兩cˆ兩⬎1, there are no fixed points at all, so the particle is never able to be trapped by the field. Also since
X
⬘
= cos共X兲−cˆ⬍0共⬎0兲 for cˆ⬎1共⬍−1兲 from Eq.共3兲, the par-ticle always lags 共leads兲 the wave; it will move back and forth with a nonzero net displacement during a cycle.Finally, for 兩cˆ兩=1 case, we have fixed points: Xe= 2n, where X
⬘
has zero maxima/minima. In this case, as indicated by Fig. 1共a兲, if 兩cˆ兩 is slightly different from unity, either a fixed point can split into two when兩cˆ兩⬍1 or there is no fixed point at all when 兩cˆ兩⬎1. As this bifurcation phenomenon always occurs at the neighborhood of兩cˆ兩=1 and the associ-ated fixed points, it is identified to be saddle-pointbifurca-tion, as shown in Fig.1共b兲.
How a charged particle surfs in a traveling-wave field and is trapped by the ratchet can be pictured in Fig. 2. In short, the key to trapping a particle is that the particle must have a speed not slower than the wave speed during its jour-ney. Consequently, such trapping is feasible only when U0
⬎c. As such, it is possible to sort charged particles by choos-ing an appropriate wave speed of the applied field. The ex-istence of stable fixed points suggests that a suspension of uniformly charged particles will be attracted toward these points, forming an organized band structure. Since these fixed points are viewed in the frame moving with the field, the particle band will synchronize with the field once it forms. As the band locates according to the particle charge 共via U0兲, particles with different charges will sooner or later
be locked into their designated positions at a given wave FIG. 1.共a兲 Phase portrait for a particle with⬎0. The arrows indicate the
directions of how the dynamical state of the particle motion evolves.共b兲 A saddle-node bifurcation.
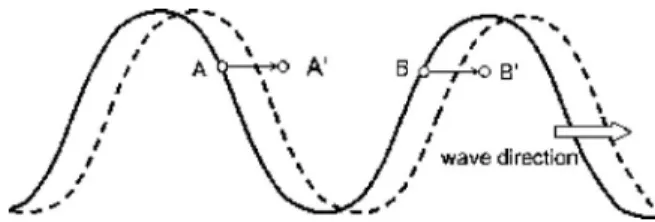
FIG. 2. Surfing and trapping of a charged particle under a traveling-wave electric field. Consider a particle starting with some speed faster than the wave speed. Suppose its initial position共at A兲 ahead of the wave 共solid curve兲. At the next instant, the particle 共at A⬘兲 will be slowed down since it experiences a weaker field共dashed curve兲. This process continues until the particle speed matches the wave’s, after which the particle movement will be synchronized with the wave. If the particle trails behind the wave共at B兲, it will first accelerate共at B⬘兲 before reaching the maximum of the field, and then decelerate afterwards as in the A-A⬘process.
204103-2 Hsien-Hung Wei Appl. Phys. Lett. 90, 204103共2007兲
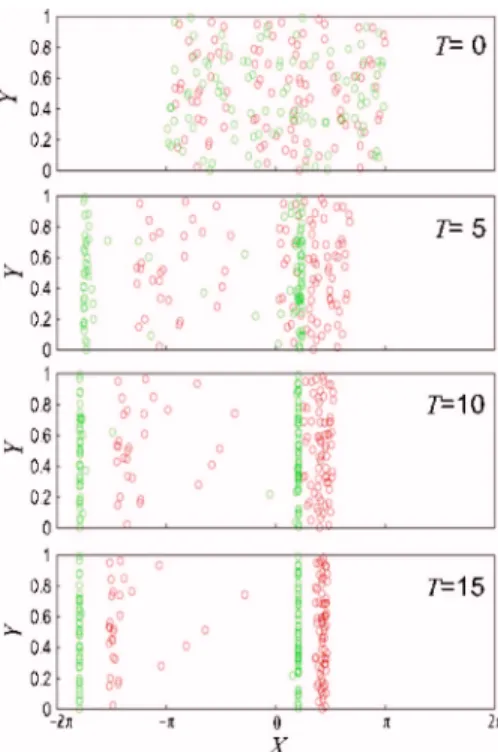
speed of the field, leading to a number of distinct particle clouds moving with the field. We carry out numerical simu-lations for Eq. 共3兲 to identify this phenomenon in Fig. 3. Such a ratchet can be applied to particle sorting or detection for a solution consisting of a variety of particle populations. As a colloidal suspensions can be characterized by correlat-ing band positions/intensities to amounts of charges/ particles, a fingerprint will be readily obtained for the suspension.
In previous studies,5,6 the particle motion can exhibit various drifting behaviors due to two-dimensional traveling fields. Our work is distinct from these studies. Our nearly 1D TWEP ratchet possesses a length scale disparity in the field and hence significantly reduces lateral drift during the trapping—it is this scale/field separation that can sustain the trapped particle clouds without being dispersed indefinitely.
It is possible to trap particles using nearly 1D TWEP in microdevices. Similar to the setup in traveling-wave
dielectrophoresis,8 a traveling field can be generated by an array of interdigitated electrodes subject to sequential phase-shifted voltages. With the electrodes of ᐉ⬃102m 共or k⬃10−2m−1兲, the device needs 10m or smaller in
depth d for minimizing lateral drift. A typical electrophoretic mobility for colloids is about 104m2/共s V兲. At an
ap-plied voltage of Ve= 10 V, one can trap particles with the wave speed c slower than U0=E0⬃Ve/ᐉ⬃103m / s. Therefore, the applied frequency = kc must be not faster than kU0⬃10 Hz for the effect at work. With the conditions
above and from Fig. 3, it takes about 10 cycles 共less than 100 s兲 for a colloidal suspension to form discrete particle bands. Such a ratchet does not require a field-dependent mo-bility for realizing biased trapping. In addition, it has a tun-able sieving capability which can be controlled by the ap-plied frequency and voltage. This nearly 1D TWEP ratchet not only provides a renewed strategy for electrophoretic separation on a gel-free basis but also offers an added advan-tage for continuous particle sorting and functional fraction-ation of colloidal suspensions.
This work is supported by the National Science Council of Taiwan under Grant Nos. NSC94-2214-E006-008 and NSC95-2221-E006-310.
1A. Manz, D. J. Harrison, E. M. J. Verpoorte, J. C. Fettinger, A. Paulus, H. Ludi, and H. M. Widmer, J. Chromatogr. 593, 253共1992兲; S. C. Jacobson, C. T. Culbertson, J. E. Daler, and J. M. Ramsey, Anal. Chem. 70, 3476 共1998兲; C. A. Emrich, H. Tian, I. L. Medintz, and R. A. Mathies, ibid. 74, 5076共2002兲.
2P. Sewer and G. A. Griess, Anal. Chim. Acta 372, 299共1998兲; G. A. Griess, E. Rogers, and P. Sewer, Electrophoresis 22, 981共2001兲. 3C. Desruisseaux, G. W. Slater, and T. B. L. Kist, Biophys. J. 75, 1228
共1998兲.
4O. Reynolds, Philos. Trans. R. Soc. London 177, 157共1886兲.
5A similar analogy can also be found in the context of electric transport of charged toner. However, it occurs when toner is in contact with the grid surface via being held by the normal field. F. W. Schmidlin, IEEE Trans. Ind. Appl. 27, 480共1991兲; F. W. Schmidlin, J. Electrost. 34, 225 共1995兲. 6S. Masuda, M. Washizu, and I. Kawabata, IEEE Trans. Ind. Appl. 24, 217 共1988兲; J. R. Melcher, E. P. Warren, and R. Kotwal, ibid. 25, 956 共1989兲. 7A. P. Washabaugh, M. Zahn, and J. R. Melcher, IEEE Trans. Electr. Insul.
24, 807共1989兲.
8L. Cui and H. Morgan, J. Micromech. Microeng. 10, 72 共2000兲; A. Ramos, H. Morgan, N. G. Green, A. Gonzalez, and A. Castellanos, J. Appl. Phys. 97, 084906共2005兲.
9Electrostatic interactions could become important when the separation be-tween particles is comparable to the Debye layer, which is obviously beyond the validity of our point-particle ansatz.
10D. W. Jordan and P. Smith, Nonlinear Ordinary Differential Equations 共Oxford University Press, Oxford, 1999兲.
FIG. 3.共Color online兲 Selective trapping of charged particles in a nearly 1d TWEP ratchet shown in the frame moving with the traveling field. The suspension consists of two types of positively charged particles: red共U0 = 0.2c兲 and green 共U0= 0.8c兲, and 100 particles for each. Initially, the par-ticles are randomly distributed with −⬍X⬍. Upon the field is applied, the particles gradually migrate toward their own trapping locations, forming respective band structures. T = t共kc兲/共2兲 measures the time normalized by the cycling period of the field.
204103-3 Hsien-Hung Wei Appl. Phys. Lett. 90, 204103共2007兲