On the Independent Spanning Trees Problem in a Hypercube

全文

(1)On the Independent Spanning Trees Problem in a Hypercube* Jinn-Shyong Yang1, Shyue-Ming Tang2, Jou-Ming Chang1, and Yue-Li Wang3 1. Department of Information Management, National Taipei College of Business 2 Department of Psychology, National Defense University 3 Department of Computer Science and Information Engineering, National Chi-Nan University Abstract* A set of spanning trees rooted at some vertex r in G is said to be independent if for each vertex v in G, v≠r, the paths from v to r in any two trees are vertex-disjoint. If the connectivity of G is k, the independent spanning trees problem is to construct k independent spanning trees rooted at each vertex. This problem is still open for general graph with connectivity greater than four. However, it has been proved that a k-dimensional hypercube (or Qk) has k independent spanning trees rooted at an arbitrary vertex. In this paper, a simple algorithm is proposed to construct k optimal independent spanning trees on Qk . The algorithm is also suitable for parallel or distributed system.. same vertex, say r, and for each vertex v ≠ r, the paths from v to r, one path in each tree, are internally disjoint (or vertex-disjoint). In this definition, we should note that the one-step path (v,r) can appear at most once. If the connectivity of G is k, the independent spanning trees problem is to construct k independent spanning trees rooted at an arbitrary vertex.. Keywords: independent spanning trees, vertex-disjoint paths, hypercube, fault-tolerant broadcasting. 1: INTRODUCTION. *. This research was supported by National Science Council under the Grants NSC94-2115-M-135 -001. Figure 1. 2. 3. 6. 7. 4. 5. 12. 13. 8. A k-dimensional hypercube, denoted by Qk , can be represented by a graph G = (V, E) with V = {0,1,2,..., 2k−1} and E = {(u,v) | v ⊕ u = 2i, 0 ≤ i ≤ k−1}, where ⊕ denotes a k-bit exclusive or operation. Thus, if k is a positive integer, then Qk is both k-connected and k-regular. The hypercube is a well-known class of graphs which may be described in terms of a product operation; i.e., Qk = Qk−1 × K2 , and Q1 = K2 is a complete graph with two vertices [4]. For example, Q4 is the product graph of Q3 and K2 , as shown in Figure 1. Hypercubes (or hypercube networks) are important due to their simple structure and suitability for developing algorithms [1,2,6,8,12,13,14,17,18,21, 22]. There are commercially available parallel computers, such as nCUBE, CM-5 and iPSC, which are equipped with hypercube multiprocessor architectures. A set of paths connecting two vertices in a graph is said to be internally disjoint if any pair of paths in the set have no common vertex except the two end vertices. Considering a graph G=(V,E), a tree T is called a spanning tree of G if T is a subgraph of G and T contains all the vertices in V. A set of spanning trees of G are said to be independent if they are rooted at the. 1. 0. 14. 15. 10. 11 9. The 4-dimensional hypercube Q4 .. Let IST denote a set of k independent spanning trees (if exists) rooted at a common vertex in G. For example, two IST’s on Q4 are shown in Figure 2. In each IST, the four paths from 0 to v (v = 1,2,...,15), one path in each tree, are internally disjoint. Since hypercubes are vertex-symmetric [9], an IST rooted at one vertex is also a solution of IST for other vertices. Thus, the two IST’s are two solutions for the independent spanning trees problem of Q4 . The study of independent spanning trees has applications in fault-tolerant protocols for distributed computing networks. For example, broadcasting in a network is sending a message from a given node to all the other nodes in the network. A fault-tolerant broadcasting protocol can be designed by means of independent spanning trees [3,11]. Fault-tolerance is achieved by sending k copies of the message along k independent spanning trees rooted at the source node. If the source node is faultless, this scheme can tolerate up to k−1 faulty nodes. In [11], Itai and Rodeh gave a linear time algorithm for solving the independent spanning trees problem in a biconnected graph. In [5], Cheriyan and Maheshwari. - 734 -.

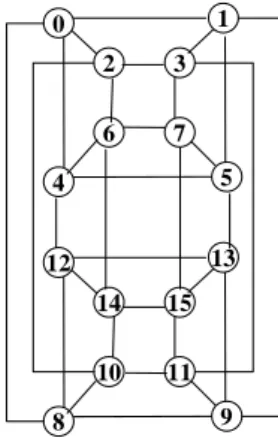
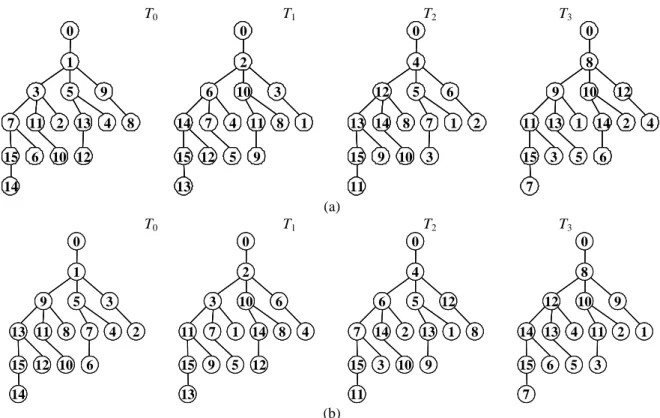
(2) as that of Ramanathan's algorithm. Meanwhile, we show that both results are optimal.. showed that, for any 3-connected graph G and for any vertex r of G, three independent spanning trees rooted at r can be found in O(|V||E|) time. In [25], Zehavi and Itai conjectured that any k-connected graph has k independent spanning trees rooted at an arbitrary vertex r. In [10], Huck has proved that the conjecture holds for planar graphs. In [7], Curran et al. have presented an O(|V|3) time algorithm for solving the problem in 4-connected general graphs. However, Zehavi and Itai’s conjecture is still open for general k-connected graphs with k > 4. In [19], Obokata et al. have solved the independent spanning trees problem by means of product graph scheme. Based on their scheme, a k-dimensional hypercube Qk can be viewed as the product graph of Qk−1 and K2 , and an IST of Qk is recursively obtained from an IST of Qk−1. However, an IST constructed using Obokata's algorithm is not optimal in terms of its average path length for k > 3. To make up this drawback, Tang et al. propose another recursive algorithm to construct an optimal IST on a k-dimensional hypercube [24]. In [20], Ramanathan and Shin also presented an algorithm for fault-tolerant broadcasting in a hypercube. Based on their algorithm, the source node sends the message to all its neighbors at first. Then, the neighbors in turn send the message to adjacent nodes based on a bit direction rule. The spirit of Ramanathan's algorithm is to construct an IST in a top-down manner. In this paper, we shall propose an algorithm that constructs an IST in a bottom-up manner. We shall also prove that the IST obtained from the proposed algorithm is the same T0. 3. The remainder of this paper is organized as follows. In Section 2, we introduce some notations and define optimal criterion for an IST on a hypercube. In Section 3, we introduce Ramanathan's algorithm. In Section 4, we propose our algorithm for constructing an IST on a k-dimensional hypercube. The last section contains our concluding remarks.. 2: NOTATION AND DEFINITION Without loss of generality, we simply consider independent spanning trees rooted at vertex 0 of a hypercube. Since vertex 0 has only one child in every tree of an IST and the child must be a neighbor of vertex 0 [23], we denote a tree in an IST of Qk by Ti where vertex 2i is the only child of vertex 0. Then, we define parent(v,i) as the parent of vertex v in Ti . The ancestor set of a vertex v in Ti , denoted by ancestor(v,i), is the set of vertices in the path from r to parent(v,i) in Ti . Based on the definition of independent spanning trees and the ancestor set, we have the following Lemma. Lemma 1. [20] Let Ti and Tj (i≠j) be two spanning trees rooted at vertex r in G. Ti and Tj are independent if and only if for every vertex v in G, v ≠ r, ancestor(v,i) ∩ ancestor(v,j) = {r}.. T1. T2. T3. 0. 0. 0. 0. 1. 2. 4. 8. 5. 9. 6. 7 11 2 13 4. 8. 10. 3. 12. 14 7. 4 11 8. 15 6 10 12. 15 12. 5. 14. 13. 1. 5. 13 14 8. 9. 6 7. 1. 9 2. 10. 12. 11 13 1 14 2. 15 9 10 3. 15 3. 11. 7. 5. 4. 6. (a) T0. 9 13 11 8. T1. T2. T3. 0. 0. 0. 0. 1. 2. 4. 8. 5. 3 7. 4. 3 2. 11. 7. 15 12 10 6. 15 9. 14. 13. Figure 2. 10. 6. 1 14 8 5 12. 6 4. 5. 12. 7 14 2 13 1. 12 8. 9. 14 13 4 11 2. 15 3 10 9. 15 6. 11. 7. (b) Two solutions for the independent spanning trees problem in Q4 . (a) Solution 1. (b) Solution 2.. - 735 -. 10. 5. 3. 1.

(3) The distance between vertex u and v in a tree is the number of edges connecting the two vertices. In [16], the path length of a tree is defined as the summation of distance between each vertex to the root. An IST is optimal if the average path length of the trees in the IST is the minimum. In [24], the authors have given some sufficient conditions for identifying an optimal IST in a hypercube. The following lemma is of vital importance. Lemma 2. [24] Given an IST of Qk . For each Ti ∈ IST (i=0, 1, …, k−1), if the distance between every vertex and the only child of the root is equal to their Hamming distance, the IST is optimal. The two IST’s shown in Figure 2 are both optimal since Lemma 2 holds. That is, for each vertex v, the distance between v and the only child of the root (i.e., 1, 2, 4 and 8 in T0, T1 , T2 and T3 , respectively) is their Hamming distance.. 3: RAMANATHAN’S ALGORITHM In this section, we introduce the algorithm proposed by Ramanathan and Shin [20]. The algorithm generates every tree of an IST from the root to the leaves. The root generates one child at first, the child then generates its own children in turn, and so forth. Since the vertices in a tree are generated in different phases, they are divided into generations. Each vertex in a Qk can be uniquely represented by a k-bit binary string, and the binary strings of two adjacent vertices differ in exactly one bit. For convenience, we number the binary string of a vertex in Qk from right to left as 0 to k−1. All already-existed vertices (except the root) are responsible for generating new vertices in a tree. The new vertices are determined by means of bit comparison. For a tree Ti in an IST, the (j+1)-th generation vertices is generated by differing from their parents at the [i+ j]k-th bit. Note that [y]x denotes y modulo x. Besides, a leaf v in Ti differs from its parent at the i-th bit. We rewrite the algorithm proposed by Ramanathan and Shin as follows. Algorithm IST_RAM Input: k. Output: An IST of Qk . Method: Step 1. Generate the first-generation vertex which is the only child of root in Ti.. For i = 0 to k−1 do parent(2i, i) = 0. Enddo Step 2. Generate next k−1 generations of vertices from already-existed vertices in Ti . For j = 1 to k−1 do For i = 0 to k−1 do. For each already-existed vertex v in Ti (v. ≠ 0) do. Let u be a neighbor of v and its [i+j]k-th bit differs from v. parent(u, i) = v. Enddo Enddo Enddo Step 3. Generate the last generation vertices, or leaves, in Ti . For i = 0 to k−1 do For each already-existed vertex v in Ti (v ≠ 0, 2i) do parent(v−2i, i) = v. Enddo Enddo End of Algorithm IST_RAM Consider the hypercube Q4 in Figure 1. The IST in Figure 2(a) is generated as follows. In Step 1, the root generates vertices 1, 2, 4 and 8 in T0, T1, T2 and T3, respectively. Using T0 as an example, the second generation vertices are {5,7}, the third generation vertices are {9,11,13,15}, and other vertices are leaves. Theorem 3. [20] Algorithm IST_RAM correctly constructs an IST of Qk in O(kn) time, where n = 2k. Theorem 4. The IST constructed IST_RAM is optimal.. by Algorithm. Proof: We prove this theorem by Lemma 2. For each tree in the IST, the distance between every vertex and the only child of the root is their Hamming distance. Thus, the output IST is optimal. If we number the binary string of a vertex in Qk from left to right as 0 to k−1, the output of Algorithm IST_RAM will be another one. For example, the IST shown in Figure 2(b) is another solution when Q4 is given.. 4: THE PROPOSED ALGORITHM The main idea of our algorithm is to compare the binary bit string of a vertex v with one neighbor of the root in a hypercube. Then, we can determine the parent of v in every tree and make all paths from v to root (one path in each tree) internally disjoint. Similar to previous section, we number the binary string of a vertex in Qk from right to left as 0 to k−1. Suppose we compare two different vertices bit by bit. Let bit i be the starting bit. The comparison is performed from bit i rightward to bit 0, and then from bit k−1 rightward to bit i+1. If bit p is the first different bit encountered, then bit p is named as the vital bit of the comparison.. - 736 -.

(4) Algorithm IST_YTCW Input: k. Output: An IST of Qk . Step 1. Connect every vertex to its parent in Ti. For i = 0 to k−1 do For each vertex v in Ti (v ≠ 0, 2i) do Compare vertices 2i and v from bit i. Let bit p be the vital bit of the comparison. If p = i then parent(v, i) = v + 2p Else parent(v, i) = v − 2p Endif Enddo Enddo Step 2. Connect vertex 2i to the root in Ti.. For i = 0 to k−1 do parent(2i, i) = 0. Enddo End of Algorithm IST_YTCW We use the IST shown in Figure 2(a) to illustrate Algorithm IST_YTCW. In T0 , for example, the binary string of vertex 11 is 1011. As comparing with vertex 1 from bit 0, the vital bit is bit 3. Since the vital bit is not the starting bit, parent(11, 0) = 11 − 23 = 3. In T1 , for another example, the binary string of vertex 13 is 1101. As comparing with vertex 2 from bit 1, the vital bit is bit 1. Since the vital bit is the starting bit, parent(13, 1) = 13 + 21 = 15. Then, we have to prove the correctness of Algorithm IST_YTCW. Theorem 5. [23] Algorithm IST_YTCW correctly constructs an IST of Qk in O(kn) time, where n = 2k. Proof: Every vertex in the path from v to the only child of the root variates according to an ordered sequence {ap2p, ap+12p+1,… , ak−22k−2, ak−12k−1, a020, a121, …, ap−12p−1}, where ai is −1, 0 or 1 and bit p is the vital bit. Since the prefix sums of the sequence in one tree is never the same as those in another tree, Lemma 1 holds for every vertex in Qk . Q.E.D. Theorem 6. The IST constructed IST_YTCW is optimal.. by Algorithm. Proof: We prove this theorem also by Lemma 2.Q.E.D. Similarly, if we number the binary string of a vertex in Qk from left to right as 0 to k−1, the output of Algorithm IST_YTCW will be another one.. 5: CONCLUDING REMARKS In this paper, we have presented a simple algorithm for constructing an IST in a hypercube. This result is optimal since the average path length of the IST is the minimum. Meanwhile, the algorithm is suitable for parallel and distributed system.. REFERENCES [ 1] B. Abali, F. Ozguner, and A. Bataineh, Balanced Parallel Sort on Hypercube Multiprocessors, IEEE Transactions on Parallel and Distributed Systems, Vol. 4, No. 5, 1993, pp.572-581. [ 2] C. Aykanat, F. Ozguner, F. Ercal, and P. Sadayappan, Iterative Algorithms for Solution of Large Sparse Systems of Linear Equations on Hypercubes, IEEE Transactions on Computers, Vol. 37, No. 12, 1988, pp.1554-1567. [ 3] F. Bao, Y. Igarashi, and S.R. Ohring, Reliable Broadcasting in Product Networks , Discrete Applied Mathematics, Vol. 83, 1998, pp.3-20. [ 4] G. Chartrand and O. R. Oellermann, Applied and Algorithmic Graph Theory, McGraw-Hill, Inc., 1993, pp.29-30. [ 5] J. Cheriyan, S. N. Maheshwari, Finding Nonseparating Induced Cycles and Independent Spanning Trees in 3-connected Graphs, Journal of Algorithms 9, 1988, pp.507-537. [ 6] G.-M. Chiu, A Fault-tolerant Broadcasting Algorithm for Hypercubes, Information Processing Letters, Vol. 66, 1998, pp.93-99. [ 7] S. Curran, O. Lee and X. Yu, Finding Four Independent Trees, SIAM Journal on Computing, Vol. 35, No. 5, 2006, pp.1023-1058. [ 8] A. K. Gupta and S. E. Hambrusch, Multiple Network Embeddings into Hypercubes, Journal of Parallel and Distributed Computing, Vol. 19, 1993, pp.73-82. [ 9] F. Harary, Graph Theory, Addison-Wesley, 1968, pp.171-173. [10] A. Huck, Independent Trees in Planar Graphs, Graphs and Combinatorics 15, 1999, pp.29-77. [11] A. Itai and M. Rodeh, The Multi-tree Approach to Reliability in Distributed Networks, in Proceedings of the 25th Annual IEEE Symposium on Foundation of Computer Science, 1984, pp.137-147. (Seen also in Information and Computation, Vol. 79, 1988, pp.43-59.) [12] S. L. Johnsson, Communication Efficient Basic Linear Algebra Computations on Hypercube Architectures, Journal of Parallel and Distributed Computing, Vol. 4, 1987, pp.133-172. [13] S. L. Johnsson and C. T. Ho, Optimum Broadcasting and Personalized Communication in Hypercubes, IEEE Transactions on Computers, Vol. 38, No. 9, 1989, pp.1249-1268. [14] J. F. Jenq and S. Sahni, All Pairs Shortest Paths on a Hypercube Multiprocessor, Proceedings of the International Conference on Parallel Processing, 1987, pp.713-716. [15] S. Khuller and B. Schieber, On Independent Spanning Trees, Information Processing Letters, Vol. 42, 1992, pp.321-323. [16] D. E. Knuth, The Art of Computer Programming, Vol. 3: Sorting and Searching, Addison-Wesley, 1973, pp.194-198. [17] P.-Z. Lee, Parallel Matrix Multiplication Algorithms on Hypercube Multicomputers, International Journal of High Speed Computing, Vol. 7, No. 3, 1995, pp.391-406. [18] F. T. Leighton, Hypercubes and Related Networks, Chapter 3 in Introduction to Parallel Algorithms and Architectures: Arrays, Trees, Hypercubes, Morgan Kaufmann Publishers, Inc., 1992. [19] K. Obokata, Y. Iwasaki, F. Bao, and Y. Igarashi, Independent Spanning Trees of Product Graphs, Lecture Notes in Computer Science 1197, 1996, pp.338-351. [20] P. Ramanathan and K. G. Shin, Reliable Broadcast in Hypercube Multicomputers, IEEE Transactions on Computers, Vol. 37, No. 12, 1988, pp.1654-1657. [21] Y. Saad and M. H. Schultz, Topological Properties of Hypercube, IEEE Transactions on Computers, Vol. 37, No. 7, 1988, pp.867-872. [22] T.-Y. Sung, M.-Y. Lin, and T.-Y. Ho, Multiple-edge-fault Tolerance with respect to Hypercubes, IEEE Transactions on Parallel and Distributed Systems, Vol. 8, 1997, pp.187-192. [23] S.-M. Tang, , Y.-L. Wang, and J.-X. Lee, On the Height of Independent Spanning Trees of A k-connected k-regular Graph, Proceedings of National Computer Symposium, Taipei, 2001, pp.A159-A164. [24] S.-M. Tang, Y.-L. Wang, and Y.-H. Leu, Optimal Independent Spanning Trees on Hypercubes, Journal of Information Science and Engineering, Vol. 20, No. 1, 2004, pp.143-155. [25] A. Zehavi, A. Itai, Three Tree-paths, Journal of Graph Theory 13, 1989, pp.175-188.. - 737 -.

(5)