Broadcasting on Incomplete WK-Recursive Networks
Min-Yang Su and Gen-Huey Chen Dyi-Rong Duh
Department of 1Zomputer Science and Information Engineering, Department of Electronic Engineering, National Taiwan University, Taipei, TAIWAN
Abstract
The WK-recursive networks, which were originally proposed by Vecchia and Sanges, have suffered from a rigorous restriction on the number of nodes. Like other incomplete networks, the incomplete WK-recursive networks have been proposed to relieve this restriction. In this paper, broadcasting on the incomplete WK-recursive networks is discussed. The proposed broadcasting algorithm is optimal with respect to message complexity. Besides, experimental results show that the heights of the broadcasting trees do n,ot exceed the diameters, and
a
high percentage of the nodes can receive the message from the source node via the shortest paths.1
Introduction
In the recent decade, a number of networks have been announced in the literature. Among them, the WK-recursive networks own two structural advantages: expansibility and equal degree. A network is expansible if no changes t o node configuration and link connection are necessary when it is expanded, and of equal degree if all its nodes have the same degree no matter what the size is.
Although the WK-recursive networks own many favorable properties (see 12, 3, 4-6, 7, 16, 17]), there is a rigorous restriction on the number of their nodes. As will become clear in the next section, the number of nodes in a WK-recursive network must satisfy d f , where d>:l is the size of the basic building block and 121 is the level of expansion. Thus, as d=4, extra 3.47=49152 nodes are required to expand from a 7-level WK-recursive network to an &level one. Almost all the announced networks have suffered from the same restriction. To relieve this restriction, some incomplete networks, such as incomplete hypercubes [SI, incomplete stars [9, 121, iincomplete rotators [ 1 I] and incomplete WK-recursive networks [I31 have been defined recently.
In this paper, a broaldcasting algorithm for the incomplete WK-recursive networks is proposed. Since the structures of the incomplete WK-recursive inetworks can be expressed as multistage graphs, the broadcasting problem is reduced to constructing spanning trees for the representative multistage graphs. The proposed broadcasting algorithm has optimal message complexity. Besides, extensive experiments have been made to verify its efficiency.
The rest of this paper is organized as follows. In the next section, the incomplete 'WK-recursive networks are formally defined, and their multistage graph representations are introduced. Broadcastings for two special situations are first described in Sections 3 and 4, respectively. Then. broadcasting for general situation is described in Section 5. The performance of the broadcasting algorithm is evaluated in Section 6 with extensive experiments. Finally, this paper is concluded in Section 7.
2 Incomplete WK-Recursive Networks and
Their Multistage Graph Representations
Hwa Shia Junior College, Taipei, T M A N
In this section we first review the structures of the WK- recursive networks. The incomplete WK-recursive networks are then defined as their induced subgraphs (graphs and networks are used interchangeably in this paper). It is also shown that the incomplete WK-recursive networks can be conveniently expressed as multistage graphs.
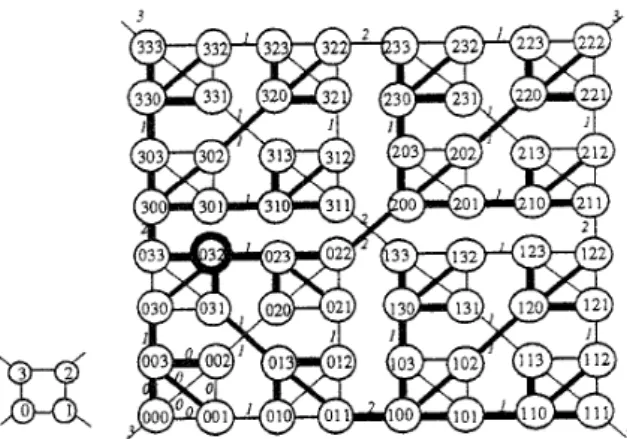
The WK-recursive networks can be constructed recursively by grouping basic building blocks. Any complete graph can serve as a basic building block. For convenience, let K(d, t ) denote a WK- recursive network of level t whose basic building blocks are each a d-node complete graph, where d>l and r2l. K(d, I), which is the basic building block, is a d-node complete graph, and K(d, t ) for t22 can be constructed by connecting d K ( d , r-lys as a d- supernode complete graph (each K(d, t-1) is regarded as a supernode). Each node of K(d, t ) is associated with a t-digit identifier.
Definition 2.1.[2] The node set of K(d, I ) is denoted by {a,la,..2...ala, I a, E ( 0 , 1, ..., d - I ) for OS&-I). Node adjacency is defined as follows: ~ , ~ u , - ~ . . . a ~ a ~ is adjacent to (1) a,la,-2...alb, where OSbld-1 and &, and ( 2 ) af-,af~2...a,+la,~l(a,Y if aj#a,-l and ujbl=aj-2= ... =ao, where 1SjSt-1 and (ajY represents j consecutive ais. The links of (1) are called substituting links, and are labeled 0. The link of (2), if existing, is called j-flipping link (or simply flipping link). and is labeledj. Besides, if a,-1=a,-2= ... =ao, there is a link, called open link, incident to node a,.Ia,-2...alao. The open link is labeled t . Since the open link is reserved for further expansion, its other end node is unspecified.
K(d, t ) contains df nodes. Since each node is incident with d-1 substituting links and one flipping link (or open link). K(d, t ) has degree d. The structures of K(4, 1) and K(4, 3) are illustrated in Figure 1. The substituting links are within basic building blocks, whereas eachj-flipping link connects two embedded K(d, j ) ' s . The open links are left for future expansion.
Definition 2.2. Define ~ , ~ ~ c ~ ~ ~ . . . c , ~ K ( d , m ) to be the induced subgraph of K(d, t ) by { c , ~ ~ c , . z . . . c , u , . ~ . . . ~ , ~ I aj E {O, 1,
...,
d - I ) for OSjSm-I), where l<m<t and c , - ~ , c,.~, ..., c, are all integers from {0, 1,...,
d - I ) .For example. refer to Figure 1, where 31*K(4, 1) is the induced subgraph of K(4,3) by {310,311,312,313).
Definition 2.3. Node ~ , ~ , a , ~ ~ . . . a ~ a ~ is a k-frontier if ak-,=
...
=al=:ao. where lSklr.By Definition 2.3, a k-frontier is automatically an 1-frontier for l l l < k . Both end nodes of a k-flipping link are k-frontiers. An embedded K(d, m ) contains o n e (nz+l)-frontier and d-1 m - frontiers. These d frontiers are 2"-1 distant from each other.
3
Figure 1. The structures of K(4, 1) and K(4, 3). The latter also shows the spamng tree rooted at 032 that results from Chen and Duhs broadcasting algorithm.
The incomplete WK-recursive networks [ 131 are induced subgraphs of the WK-recursive networks. If we number the nodes of K(d, t ) according to their lexicographical order, then an N-node incomplete WK-recursive network is the subgraph of K(d, t ) induced by the fust N nodes. Throughout this paper, we use IK(d,
r)
to denote an N-node incomplete WK-recursive network, where dr-kN<d' and N is a multiple of d.The coeficienr vector of IK(d, I) is uniquely defined as a ( f -
1)-vector (b,,, blv2,
....
b,) such that N=b,-ld'-l+br.2d'-2+ ...+
bid,where O$b,Sd-1 for all 1SmSr-1. IK(d, t ) with coefficient vector (bf-l, bc2, ..., b , ) contains b, embedded K(d, m)k, i.e., br-lb,-2... b,+,O.K(d. m), bf.lbf-2...b,+ll.K( d , m),
...,
and b,-)b,-2... b,+,(b,,,-l).K(d. m), where lSm5f-1. For example, IK(5, 6) with coefficient vector (2, 3, 0, 4, 2) contains the following embedded K(d, m)'s.O.K(5, 5 ) , l.K(5, 5 )
20.K(5, 4), 21.K(5, 4), 22.K(5, 4)
2300,K(5, 2), 230l.K(5, 2 ) , 2302.K(5, 2), 2303.K(5, 2) 2304O.K(5, l ) , 23041 .K(5, 1)
Figure 2 shows the structure of IK(4, 3) with coefficient vector (3, 2). In the rest of this paper, a coefficient vector (b,-], b f - 2 , ..., b,) is written as (b,-,, b,-2, ..., b,, *), where 1SiSt-1, provided b,rO and bl-1=b,-2=
...
= bl=O. For example, (2, 0. 4, 0) is written as ( 2 , 0, 4, *), and ( 2 , 3, 4) is written as ( 2 , 3, 4, *).Figure 2. The structures of IK(4.3) with coefficient vector (3, 2).
Let S, represent the subgraph of IK(d, t ) with coefficient vector ( b , - , , b,,,
...,
b,, * ) induced by the nodes of br-lbI.2... b,+,O.K(d, m), b , ~ l b l ~ 2 . . . b m + l l ~ K ( d , m), ..., and br.lbr.2...bm+~(bm- 1).K(d, m), where i<m$t-1. For example, when IK(5, 6) with coefficient vector (2, 3, 0, 4, 2, *) is concerned, S5 contains O,K(5, 5) and l.K(5, 5), and S2 contains 230O.K(5, 2), 230l.K(5, 2), 2302.K(5, 2) and 2303.K(5, 2). W e note that there is an m- flipping link between any two of these b, embedded K(d, m)'s within S,.According to the discussion above, the structure of IK(d, t) with coefficient vector (b,-,, br-2,
...,
bi, *) can be expressed as a (r-i)-stage graph, regarding each S, as a stage. The (t-i)-stage graph is denoted by SI-I+Sr.2+ ...+Si.
For example, IK(5, 6) with coefficient vector (2, 3, 0,4, 2, *) can be expressed as a five-stage graph as shown in Figure 3. For simplicity each embedded K(d, m ) within S, is drawn as a circle, and the one b , .lb,.2... b,+,j,K(d, m ) where OSjSb,-l, is denoted by CA. All the m- flipping links between these circles are omitted for conciseness. Also note that for r - 1 2 m l n l i . Sm+Sm-,+ ... +S, itself forms an embedded IK(d, m+l) with coefficient vector (b,, bm-l, ..., b,, *), in which each node has its identifier prefixed with bf.lbl-2...bm+l.There are min{ b,, b,.l ) m-flipping links between S, and S,.
1, each connecting
c',
and Ci.1 for some OSjSmin { b,, bm-l ) - 1.Besides, for t-lZu>v>i and u-v>l, there may exist a u-flipping link between S , and S,. If such a link exists, it is called a jumping u-flipping link. A necessary and sufficient condition for the existence of jumping flipping links has been suggested in [14] as follows.
s5 s 4 s 3 s2
Figure 3. The multistage graph representation of IK(6, 5) with coefficient vector (2, 3, 0 , 4 , 2, *).
Theorem 2.1.1141 For IK(d, t ) with coefficient vector (bf-l, b,-2,
....
b,, *), one jumping u-flipping link exists between S, and S, if and only if b,>b,-l=bu-2= ... =bv+l<bv, where f-llu>v>i and u - v p l . Moreover, this jumping flipping link connects C: and C,", where e=b,.l=bu.2= ... =bv+l.In the rest of this paper we use .I,'" to denote the jumping u-
flipping link between C : and C t (refer to Figure 3 for illustration).
The structure of Sf-1+Sr.2+ ... +SI is further detailed as follows. Since each
e,,
where 1-12 m2i and 05j5bn,-l, is a K(d,other hand, the links incident to C;” include (1) b,-1 m-flipping links connecting C,, C,, ..., m , m ,
...,
and C 2 , respectively; ( 2 ) one m-llipping link connecting C i l ifj<b,-,-l, or one jumping m-flipping link connecting C:, where k m - 1 , if j=b m- I =bm-,= ._. = bl+]<bil; (3) one (m+l)-flipping link connecting CA+, i f j 5 bm+l-ly or one jumping h-flipping link connecting C i , where h>m+l, if bh>bh-l.=&h-2= ... =b,+]=j. Both end nodes of (1) are b,-lb,-2...bm+j(x)m E C;” and bl~lb,-2...b,+Ix(j)m E e m , whereOln<b,-l and x#j. Both end nodes of (2) are bl-lbf-2...b,+j(b,)m E C ~ and br.lbf.2...bm+lbm~)m E C i l (or E C:). Both end nodes of
E
cjh)
and b,-lbf-2...bm+2bm+l(j)m+1 E Cb.Since the structurle of IK(d, t ) can be expressed as a multistage graph, message-optimal broadcasting in IK(d, t ) is equivalent to constructing a spanning tree for the multistage graph. The spanning tree is also referred to as broadcasting tree when broadcasting is concemed. Suppose the source node is r E
S,
and broadcasting is performed on IK(d, f) with coefficient vector (b,-l, b,,, ..., b , *), where t-122i. The resulting spanning tree is denoted by ST(r-I, i, r,z).
In subsequent sections, without loss of generality, we describe the broadcasting algorithm by explaining how to construct ST(m, n , r,z )
in Sm+Sm-]+...
+S,, where t- l>m>z>n>i. In the next two sections, we first construct ST(m, n, r,z)
for two special cases: z=m and z=n. Then, constructing ST(m, n, r,z )
for arbitrayz
ranging from n to m is discussed in Section 5. b - IcJ-I
cJ+
0 1 (3) are bl-lb,-2...bm+j(tlm+l)m+1 Eck+l
(Or b,-1b,-2..-bh+d(bh)~3
Constructing S T ( m ,
n ,
r , m )
Several basic dissemination patterns lay the foundation of our construction algorithm for ST(m, n, r, m). The purpose of this section is to introduce them and show how they can be used to construct ST(m, R , r, m). First of all, we have to review Chen and Duh’s broadcasting algorithm [2] for K(d, t ) because the algorithm will be executed by the dissemination patterns. Chen and Duh’s algorithm requires a stack of length f + l (a bit array of length r+l for real implementation), which keeps the labels of links. to be carried with the message. Initially, the source node pushes the label t into the stack and disseminates the message over all its incident links but the one with label t. Once a node receives the message via its one incident link with label, say k, it further disseminates the. message by executing the following steps.
1. Pop elements of the stack until the top element is greater than
k .
2. Push k into the stack.
3. Disseminate the message over those incident links whose labels do not appear in the stack.
For illustration, Figure 1 shows with bold lines the broadcasting tree that results from executing Chen and Duh’s algorithm on K(4, 3 ) with source node 032. (that is, the spanning tree rooted at node 032). ‘The foliowing lemma has been proved in
P I .
Lemma 3.1.[2] Starting from any node, Chen and Duh’s algorithm can disseminate a message to each node of K(d, t ) exactly once. Moreover, Ithe resulting spanning tree has height at most 2-1, which is the diameter of K ( d , f).
With slight modification, Chen and Duh’s algorithm can disseminate a message within any embedded K(d, l ) , where K k t . W e assume r=rf~lr,~2...rlro. A spanning tree of r,-lr,-z ...rl+lrl.K(d, 1)
rooted at node r can be obtained by executing Chen and Duh’s algorithm, provided step 3 is modified as follows.
3. Disseminate the message over those incident links whose
The modified step 3 restricts the message dissemination inside the embedded K(d, 1). As a consequence of Lemma 3.1, the resulting spanning tree has height at most 2’-1.
Now we are going to construct ST(m, n, r, m ) in I K ( d , 1 )
(=Sf-1+S,-2+ ... +Si), where t-l>m>n>i. Recall that S, contains b, embedded K(d, m)’s that are completely connected by m- flipping links. Moreover, since r E S,, we have r=r,-lrr-2...
rm+lr ,... rIr0=b, -lb,~~...bm+lrm...rlrO E b,-, br-2...bm+l r,.K(d, m ) , where Olr,Sb,-l. By the aid of the modified Chen and Duh’s algorithm, ST(m,
m, r,
m ) , i.e., a spanning tree of S, rooted at node r, can be constructed as the union of the following components.0 A spanning tree of bl-lbr-2...bm+lrm.K(d, m) rooted at node r.
Link set {(b,~lb,~z...bm+lrm(x)m, b,-lbr-2...bm+lx(rm)m) I O%b,-l Spanning trees of b,.lbf-~...b,+lx~K(d, m ) rooted at b,-lb,-z...
labels are smaller than 1 and do not appear in the stack.
and ~ r , ) .
bm+lx(rm)m for all Olnlb,-l and xfr,.
Constructing S T ( m , n , r , m ) for m>n proceeds with examining Sm+Sm-l+
...
+S,
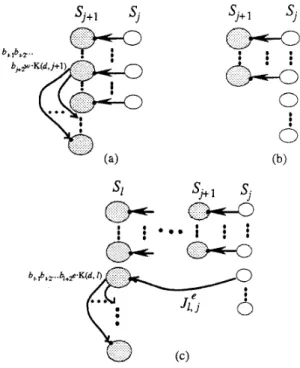
from the left to the right and recursively executing the following five dissemination patterns. Pattern A.of the following components (refer to Figure 4(a)). ST(m, m, r, m ) .
Link (b,-lbl-2 -bm+ 1 rm(bmIm, b,-,br-2...bm+lbm(~m)~). ST(m-1, n, r’, m-1), where r‘=b,~lbl-2...b,+lb,(r,)m. Pattern B .
If r,=b,-, and there exists one jumping flipping link from S, to some SI (i.e., J m , l ) , where m - l > k n , then by Theorem 2.1 we have bm>bm-]=bm.,=
...
= b l + ] < b l , and S T ( m , n , r , m ) is constructed as the union of the following components (refer to Figure 4(b)).ST(m, m, r, m).
Jumping flipping link ( bt- l b,- 2. .. bm+l rm( bm)mr b,-lb,-2...bm+l ST(m-1, n, r‘, I ) , where r‘=b, ~lb,~2...b,+lb,(rm)m=bl~lb,~z...bl+l
If rmSbm-l-l, then ST(m, n, r, m) is constructed as the union
bm-1
bm(ynJm).
( r,)l+l .
Pattern C .
If rm>b,-l and there exists one jumping flipping link from S, to some
SI,
where m - l > l S n , then S T ( m , n , r , m ) is constructed as the union of the following components (refer to Figure 4(c)).S T ( m , m , r, m ) .
Link set { (b,.lb,.2...b,+lx(b,)m, b , . l b , . z . . . b m , , h , l l ( ~ ) m ) I O a S Spanning trees of b,-,b,~2...b,+lb~~K(d, m - I ) rooted at b,-lb,-2 bm-l-l ).
* Jumping flipping link (bt-~bl~~...bm+lbm.~(bm)m, bf-lbr-2 ... bm+l ST(m-2, n , r', 1), where r'=b, .lbr-2...bm+lbm(bm-l)m=br-ibr-2... bm(bm-Ilm).
bl+l (bm-1 )'+I,
Pattern
D.
If rm2bmF1 and there is no jumping flipping link from S, to some S,, where m-l>12n, then we determine the leftmost jumping flipping link, say J e , in
s,+s,-]+
...+s,,
if it exists.Since J u , v is the leftmost one, by Theorem 2.1 w e have b,>(rm2)bm-,2b,-22 ... 2b,>b,-,= bu-2= ... =bv+]<bv and e=bu-l= bu-2= ... Then ST(m, n, r, m ) is constructed as the union of the following components (refer to Figure 4(d)).
U , v
e
ST(m, m, r, m ) .
Link sets ( (b,lb,2...bj+lx(bj~, bf.1b,2...bj+lbj(x~) I O S b j - l - l ) for all u<j<m.
Spanning trees of b,lb,2...bj+lb~~K(d,j-l) rooted at bl.lbr.2... .bj+]bj(xY for all Olxlbj-l-l and all uSjSm.
Jumping flipping link ( b r ~ l b , ~ 2 . . . b u + l e ( b u ) u , bl-lbr.2 ... bu+l ST(u-2, n . r', v), where r'=b l . l b r ~ 2 . . . b u + l b u ( e ) u = b r . I b f ~ z . . . b,(e)").
by+, (e)Y+l.
IfJ;," does not exist, then ST(m, n, r, m ) is constructed as the union of the first three components above, with substituting n + l for U.
Note that the last components in Patterns B , C , and D are spanning trees of the form ST(m', n, r', k), where m'=k or m 5 k and bm=bm,.l=
...
=bk+]<bk. If m'=k, ST(m', n, r', k ) is constructed recursively. Otherwise, ST(m', n, r', k ) is constructed as follows.0
p
0 ;,
;
0Figure 4. Five dissemination pattems for constructing ST(m, n, r , m ) . (a) Pattern A . (b) Pattern B . (c) Pattern C. (d) Pattern D . (e) Pattern E .
Pattern E .
ST(m', n, r', k), where b,3=bm,bl= ... =bk+]<bk and m S k n , is constructed as the union of the following components (assuming h=b,.=b,-,=
...
=bk+]) (refer to Figure 4(e)).S T ( k , n, r', k).
Link sets {(bclb,.z...bj+,bj(n)i, bl.lb,.2...bj+lx(bj)i I 05x5 h - 1 ) for all k<jSm'.
Spanning trees of b,.lbf-*...b,+lx.K(d, j ) rooted at bl-lb,-2 ... b,+,x(b,y'for all Olxlh-1 and all k<jSm'.
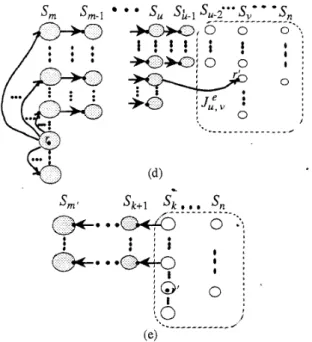
With these patterns, S T ( m , n , r, m ) , where m>n, can be constructed recursively. For example, let us consider IK(d, 11) with d>5 and coefficient vector (4, 5, 4, 2, 2, 4, 2, 2, 1, 5. U).
Assuming r ~ 4 5 3 . K ( d , 8), ST(8, 2 , r, 8 ) can be constructed as follows (refer to Figure 5(a)). First, Pattern C is applied because r8=3>2=b7 and there exists one jumping flipping link from S , to S g . A spanning tree of S,+S, rooted at r is thus obtained. Then Pattern E is applied to construct ST(6, 2, r', 5 ) ,
where r'=454(2),= 45422(2)6, and the spanning tree of Ss+S7 rooted at r grows by augmenting ST(5, 2, r', 5) and the nodes of S6. ST(5, 2, r', 5) can be obtained by applying Pattern
D.
4 Constructing
S T ( m ,
n , r , n )
In this section, we aim to construct S T ( m , n , r. n). The construction algorithm contains three basic dissemination patterns: Pattern F , Pattern G, and Pattern H . A variable w is used by the algorithm. Initially, w is set to r,,, where z r l - l r f - 2...r1r0 is assumed. and ST(n, n , r, n ) is constructed as an initial spanning tree. The current spanning tree, assuming STU, n, r, n ) and nSj<m, will grow toward the left when the patterns are applied. The details are shown as follows.
=45422(2)6 0
0
(a)s10 s9 sf! s7 s6 s5 s4 s3 s2
SI
0
Figure 5 . Examples. (a) ST(8, 2, r, 8 ) , where r belongs to 453.K(d, 8). (b) ST(9, 4, r, 4 ) , where r belongs to 4542240.K(d, 4)
Pattern F .
If bjlbj+l, then STU, n, r, n ) grows into STo+l, n, r, n ) by augmenting the following components (refer to Figure 6(a)).
Link set { ( b
,
k ~ , . ~ . ..
bl+ b,+ ( xp+
, b,. b,.2...
b j+2x( bj+ Y + l ) ISpanning trees of b,lE,,2...bj+2n.K(d,j+l) rooted at br-lbr-2... Link set { (b,.lb,-2...bj,.2w(yy+1, b,-lb,.z...bj+zy(w)j+l) I bjSy< Spanning trees of b,.lE),.2...bj+2y.K(d, j + l ) rooted at b,-1b,-2...
The subnetwork b,-l~b,2...bj+2w.K(d, j + l ) is responsible for disseminating the messalge to b,lb,.2...b,+2y.K(d, j+l) for all b$jSbj+l-l. They are not allowed to receive the message directly from S,.
Pattern G .
If bj>bj+l and there :is no jumping flipping link from
S
’
to some Si, where m?l>j+l., then STO, n , r, n ) grows into ST(j+l,n, r, n ) by augmenting the: following components (refer to Figure 6(b)).
Link set { (b,-lb,.2...b,+2,b,+l(xp1, b,-lb,-2...b,+2~(b,+l~+~) I 0% Spanning trees of b,.lb~,.2...b,+2x.K(d,j+l) rooted at b,-lb,-z... Pattern H .
If bj>bj+] and there exists one jumping flipping link from S, to some SI, where mll>j-tl, then STU, n , r, n ) grows into ST(I,
09Xlb,- 1 ) .
bj+2x(bj+lY1 for all 0 9 S b j - l . bj+l-1)*
b,+Zy(w)’+’ for all bjlySbj+l-l.
bj+l-lI.
b,+2x(b,+l
Y+l
for all Olx:$b,+l-
1.n, r, n) by augmenting the following components (refer to Figure 6(c), where e=bl-l=bl-2=
...
=b,+] is assumed.Link sets { (b,-lbc2...bs+lbs(~)S. br-lbf-2...bs+,~(bs)5) I O e s e - 1 ) Spanning trees of bf-,b,-,...b,+,x.K(d, s) rooted at bf-lbf-2... Jumping flipping link (b,-lb,2...bl+lb,(e)’, b,-lb,-2...b,+le(bl)’). Spanning tree of b,.lb,-2...bl+1e.K(d, I ) rooted at b,-lb,-2... Link set ((b,~lb,-2...b,+le(y)~, b,-1b,-2...bl+1y(e)9 I e + l l y $ b , - l ) . Spanning trees of b,-lb,.z...bl+ly.K(d, I ) rooted at bf-lb,-z...
Besides, w is updated to e after Pattern H is executed. The purpose of this change is to maintain the height of ST(m, n, r, n )
as small as possible. for all j<sll.
bs+lx(b,)s for all OSxle-1 and all j c s l l .
bl+le(b,Y.
bl+ly(e)’ for all e+llySb,-l.
Sj+1 sj
Figure 6. Three dissemination patterns for constructing ST(m, n, r, n). (a) Pattem F. (b) Pattern G . (c)Pattem H .
By the aid of the three patterns, S T ( m , n , r , n ) can be constructed from the right to the left. For example, refer to Figure 5(b) where r ~454224O.K(d, 4 ) and ST(9,4, r, 4 ) is shown. The IK(d, 1) has d>5, t = l l , and coefficient vector (4. 5, 4, 2, 2, 4, 2,
2, 1, 5 , *). Initially, ST(4, 4 , r , 4 ) is constructed as an initial spanning tree, and w is set to r,=O. Since b,=2<4=bs. Pattern F is first applied and ST(4, 4, r, 4 ) grows into ST(5, 4, r, 4). Next, Pattern H is applied and the current spanning tree becomes ST(8, 4, r, 4). Also w is updated to 2 (=b&). Finally. ST(9, 4,
r, 4 ) results after Pattern F is applied.
5
Constructing
S T ( m ,
n ,
r ,
z )In this section, we explain how to broadcast in IK(d, f) by constructing ST(m, n, r,
z),
where m S 5 n . Since the two cases of z=m and z=n have been discussed in the previous two sections, weonly need to consider m>z>n. Without loss of generality, we assume r E b,.,br.2...bz+la-K(d,
z ) ,
where OlaSb,-l. First of all,we have to determine whether or not there is a jumping flipping link passing S,, i.e., whether or not some J e exists such that
m?u>z>v>n. If not, S T ( m , n , r ,
z )
can be obtained by first constructing ST(z, n , r ,z )
and then expanding it to ST(m, n, r, 2). The former can be done in the same way as described in Section 3. The latter can be done just like in Section 4, but ST(z, n, r,z),
instead of ST(z, z, r,z),
is regarded as the initial spanning tree, and w is initialized with a.If such a J e exists, by Theorem 2.1 we have b,>b,-l=bu-2=
._. =bv+l<bV and e=bu.l=bu.2= ... = b v + l . S T ( m , n , r , 2) is constructed according to the following two cases.
Case 1. z=u-1.
First, ST(u, n, r,
z )
is obtained by combining together the following components (refer to Figure 7(a) where a=e-1 isu , v
,,Y
a S S U m e d ) .
= ST(z, n, r, z).
Link set {(br.lb,.2...bu+lbu(x)u, br-lbl.2...bu+lx(bu)u) I O2xxle-1).
0 Spanning trees of b,.lb,.2...b,,lx~K(d, U ) rooted at bl-lb,.2...
bn+lx(bu)u for all O<_x<e-1.
Jumping flipping link (br-lbl.2...bu+lbu(e)U. bl-lbt-2...bu+l 4bU)").
= Spanning tree of b,1b,-2...bu+le.K(d, U ) rooted at br.lbr-t... bu+le(bu)u.
Link set { (b,-lb,-2...bu+la(y)u, bl.lbr-2...bu+ly(a)U) I e+llySb,- 1).
Spanning trees of b,~lb,~...b,+ly.K(d, U ) rooted at bl-lbr-2... b,+,y( a)" for all e+lSySb,-1.
The subnetwork b,~,b,2...b,+le~K(d, U ) in S, receives the message via
i.ey
in order to reduce the transmission length. Then, ST(u, n, r,z )
grows into ST(m, n, r, z) by augmenting the nodes of Sm+Sm.l+ ... +Su+l, which can be done almost the same as in Section 4 except that ST(u, n, r , z) is regarded as the initial spanning tree and w is initialized with a.Case 2. ~ u - 1 .
First, ST(u, n, r,
z)
is obtained by combining together the following components (refer to Figure 7(b) where a=e-1 isaSSUmed).
* ST(z, n , I , 2).
* Link sets { (br-lbr-2...bj+lbj(xy', b,-lbr-2...bj+l~(bjy') I O i x l e - 1 ) for all z<jlu.
a Spanning trees of b,-lb,-2...b,+l~.K(d, j ) rooted at b,.1b,.2...
bj+lx(bjy for all 0-e-1 and 11 z-=j5u.
Jumping flipping link (b,.lb,.2...bu+lbu(e)U, b,-lbr-2...bu+l
4 b U ) " ) .
0 Spanning tree of b,~lb,.2...b,+le~K(d, U ) rooted at b,lb,.2...
bU+la.b"Y.
0 Link set { ( b , . ~ br-2...bu+le(y)u, b,.lb,~2...b,+ly(e)") I e + l l y l b , -
11.
0 Spanning trees of b,.,b,.2...bu+ly~K(d. U ) rooted at b,.,b,.2...
b,+ly(e)Y for all e+lSylb,- 1.
Like Case 1, ST(u, n, r. z) then grows into ST(m, n, r , z) by augmenting the nodes of Sm+SmSl+ ... +Su+l with S T ( u , n, r , z) being the initial spanning tree and e being the initial value of w. A distributed algorithm (in pseudo codes) for broadcasting on IK(d, f) can be found in [ 151.
s,
*- - S U C 1
s,
s,
- - -
s,
'
s,
*
*
*Figure 7 . Illustration of ST(m, n, r, z). (a) z=u-1. (b)
z a -
16 Experiments and Results
Clearly our broadcasting algorithm achieves optimal message complexity, because each node receives the message exactly once. Besides, extensive experiments had been made to verify the efficiency. The following four algorithms as well as our broadcasting algorithm were implemented for the need of our experiments.
Su, Chen, and Duh's algorithm for computing the diameter of I K ( 4 f ) [ 131.
Remark. Using the prune-and-search technique [ 103, the algorithm can compute the diameter of IK(d, t ) in O ( t ) time. Moreover, the farthest pair of nodes can be determined simultaneously. Note that although the diameter of IK(d. f ) can be computed, no formula is available for computing it.
Su, Chen, and Duh's shortest-path routing algorithm for IK(d, f )
Chen and Duh's shortest-path routing algorithm for K(d, r ) [2]. Chen and Duh's broadcasting algorithm for K(d. t ) [2] (also reviewed in the beginning of Section 3).
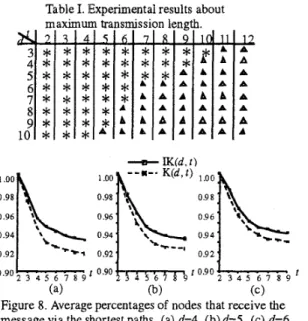
W e first compared the maximum transmission length, i.e.. the height of ST(r-1, i, r, z), with the diameter of IK(d. I). Table I shows the experimental result. For each of the entries marked with
*,
the experiment was made exhaustively. That is, for each d'-'ulr<d', we let each of the N nodes act as the source node and then determine the height of the corresponding ST(f-1. i, r,z).
Our experimental result shows that all ST(1-1, i, r, z)'s have their 1141.heights bounded above: by the diameter. The diameter was computed by Su et al.'s algorithm [ 131.
On the other hand, fior each of the entries marked with A, we randomly chose lo5 experiment instances (instances for short). Here, an arbitrarily selected value of N combined with an arbitrarily selected source node r forms an instance. Our experimental result shows that their corresponding ST(t-1, i, r,
z)'s have their heights bounded above by the diameters. Moreover, the experiment was also made by selecting peripheral nodes as r. A node in a network is said to be a peripheral node [ l ] if the distance between it and its farthest node is equal to the diameter of the network. Su et al.'s algorithm [13] can find two peripheral nodes as well. It is clear that the height of ST(t-1, i, r, z ) is at least the diameter if r is a peripheral node. Our experimental result shows Chat the height of ST(t-1, i, r, z) for peripheral node r is just the same as thediameter.
In addition to the maximum transmission length, we also investigated how close to the shortest paths the transmission paths are. Figure 8 shows the average percentages of nodes that receive the message from the source node via the shortest paths. Chen and Duh's broadcasting algorithm [2] for K(d, t) was adopted in the experiment. The experiment proceeded as follows. First, 1000 instances were randomly chosen for both IK(d, f) and K(d, t), Here a selected value of N combined with a selected source node r forms an instance of IK(d, f), whereas a selected source node alone forms an instance of K(d, t ) . For each of the chosen instances, the percentage was computed by the aid of Su et al.'s algorithm [14] and Chen and Duh's algorithm [ 2 ] . T h e two algorithms can compute the distance of arbitrary two nodes in IK(d, t ) and K(d, t), respectively. The average percentages for IK(d, f) and K(d, t) were then computed for the 1000 instances (we found in the experiment that all average percentages got stable after running 1000 instances).
Table I. Experimental results about
P
A A A A A A A (a) (b) (c)Figure 8. Average percentages of nodes that receive the message via the shortest paths. (a) d=4. (b) d=5. (c) d=6.
7
Concluding
Remarks
In this paper we have shown that the i n c o m p l e t e WK- recursive networks can be conveniently represented with the multistage graphs, and thus broadcasting on the incomplete WK- recursive networks is equivalent to constructing spanning trees for
the corresponding multistage graphs. The resulting broadcasting algorithm achieves optimal message complexity. Besides, experimental results showed that t h e maximum transmission length does not exceed the diameter, and a high percentage of nodes can receive the message from the source node via the shortest paths.
REFERENCES
[l] [2]
F. Buckley and F. Harary, Disfance in Graph, Addison- Wesley, 1990.
G. H. Chen and D. R. Duh, "Topological properties, communication, and computation on WK-recursive networks," Networks, vol. 24, no. 6, pp. 303-317, 1994. D. R. Duh and G. H. Chen, "Topological properties of WK- recursive networks," J . of Parallel and Distributed Computing, vol. 23, no. 3, pp. 468-474, 1994.
R. Fernandes and A. Kanevsky, "Substructbre allocation in recursive interconnection networks," in Proc. of Int. Cwn$
on Parallel Processing, vol. I, 1993, pp. 31 9-322.
R. Femandes, D. K. Griesen, and A. Kanevsky, "Efficient routing and broadcasting in recursive interconnection networks," in Proc. of the Int. Con5 on Parallel Processing, R. Femandes, D. K. Friesen, and A. Kanevsky, "Embedding rings in recursive networks," in Proc. of Int. Symp. on Parallel and Distributed Processing, 1994, pp. 273-280. [7] A. Iazzetta, C. Sanges, and U. Scafuri, "Special multicast
wormhole routing for WK-networks," manuscript.
[8] H. P. Katseff, "Incomplete hypercubes," IEEE Trans. on
Computers, vol. C-37, no. 5, pp. 604-608, 1988,
[9]
S.
Latifi and N. Bagherzadeh, "Incomplete star: an incrementally scalable network based on the star graph,"IEEE Trans. on Parallel and Disrributed Systems, vol. 5 ,
no. 1, pp. 97-102, 1994.
[lo] D. T. Lee and F. P. Preparata, "Computational geometry - a survey," IEEE T. C., vol. C-33, pp. 1072-1101.
Dec.
1984. [ l l ] S . Ponnuswamy and V. Chaudhary, "Embedding of cycles in rotator and incomplete rotator graphs,'' in Proc. of Int. Symp. on Parallel and Distributed Processing, Oct. 1994, [12] C. P. Ravikumar, A. Kuchlous, and G. Manimaran, "Incomplete star graph: an economical fault-tolerant interconnection network," in Proc. of Int. Con5 on Parallel Processing, vol. I, 1993, pp. 83-90.[13] M. Y. Su. G. H. Chen, and D. R. Duh, "Topological properties of incomplete WK-recursive networks," Tech. Rep. NTUCSIE 95-06, National Taiwan Univ., Taipei. 'Taiwan, March 1995.
[14] M. Y. Su, G. H. Chen, and D. R. Duh, "A shortest-path routing algorithm for the incomplete WK-recursive networks," Tech. Rep. NTUCSIE 95-07, National Taiwan Univ., Taipei, Taiwan, July 1995.
[15] M. Y. Su, G. H. Chen, and D. R. Duh, "A broadcasting algorithm for incomplete WK-recursive networks," Tech. Rep. NTUCSIE 95-09, National Taiwan Univ., Taipei, Taiwan, December 1995.
[16] G. D. Vecchia and C. Sanges, "A recursively scalable network VLSI implementation," Future Generation Computer Systems, vol. 4, no. 3, pp. 235-243. 1988. [17] G. D. Vecchia and C. Sanges, "An optimized broadcasting
technique for WK-recursive topologies," Future Generation Computer Systems, vol. 4, no. 3, pp. 353-357. 1989190. 131 [4] [5] 1994, pp. 51-58.