THE STUDY OF A NEW PERFECT HASH SCHEME

[131 R. L.Mattson,J.Gecsei, D. R. Slutz, and I. L.Traiger, "Evalua-tiontechniques for storage hierarchies," IBM Syst. J., voL 9, pp. 78-117, 1970.

[14] J. B. Morris, "Demand paging through the use of workingsetson the MANIAC II," Commun. Ass. Comput. Mach., vol. 15, pp. 867-872, Oct. 1972.

[151 J.-F.Paris, personal communication, Feb. 1981.

[16] B. G. Prieve, "A page partition replacement algorithm," Ph.D. dissertation, Univ. California, Berkeley, 1974.

[17] J. Rodriguez-Rosell and J. P. Dupuy, "The design, implementa-tion, and evaluation of a working set dispatcher," Commun. Ass. Comput.Mach.,voL 16, pp.247-253, Apr. 1973.

[18] A. J. Smith, "A modified working set pagingalgorithm," IEEE Trans.Comput., voLC-25, pp.907-914, Sept. 1976.

[19] A. J. Smith, "Two simple methods for the efficient analysis of memory address trace data," IEEE Trans. Software Eng., vol. SE-3, pp. 94-101, Jan.1977.

[201 J. R. Spirn, "Program locality and dynamic memory manage-ment," Ph.D. dissertation,PrincetonUniv.,Mar. 1973.

Domenico Ferrari (M'67), for a photograph and biography, see p. 79 of the January1983 issue of this TRANSACTIONS

Yiu-Yo Yih received theB.E. degree in com-puter engineering from theUniversityof Michi-gan, Ann Arbor, and theM.S. degree in com-puter science fromtheUniversityof

California,

Berkeley.

He joined

Bell

Laboratories,

Holmdel,

NJ,

as

amember ofthe technical staffin May 1980. * His interests include operating systems and pattem recognition. He iscurrently working

towards a Ph.D.degreein computerscience at RutgersUniversity.

The

Study

of

a

New

Perfect

Hash

Scheme

M.W. DU, MEMBER, IEEE,T. M. HSIEH, K. F. JEA, AND D. W. SHIEH

Abstract-Anewapproach isproposed for the design of perfect hash functions. Thealgorithms developed canbeeffectively appliedtokey setsof large size. The basic ideas employed in the construction are rehash and segmentation. Analytic results aregiven which are appli-cable when problem sizes are smalL Extensive experiments have been performed to test the approach for problems of largersize.

IndexTerms-Hashing, perfect hash functions, rehash, segmentation.

I. INTRODUCTION

ASHING has been considered as an effective means to

H

organize and retrieve data in program design and has

been widely used in databasemanagement,compiler construc-tion, and many other applications. In order to use hashing

techniques in a specificapplication, one hasto first choose a suitable hash function, then select a method for collision

resolution. Quite a number ofways have been proposedto design hashfunctions [2], [13], [16], [17],

[211.

Two

colli-sionresolving methods, chainingandopenaddressing,have also

been exploredinmany papers [12], [15] [17]

-[201,

[23]. Ifa hash function can be found whichisone-to-one from the set ofkeysin thekeyspace tothe addressspacethen that Manuscript receivedApril 20, 1981; revisedDecember27, 1982. This workwassupported in part by theNational Science CouncilofR.O.C. under Grant NSC-68E-0201-04(05). Partofthis paperwas presented atCOMPSAC'80,Chicago, IL, October 1980.

M. W. Du is with the Institute of Computer Engineering, National ChiaoTungUniversity, Hsinchu, Taiwan, R.O.C.

T. M. Hsieh is with the Institute ofElectronic Engineering,National Chiao Tung University, Hsinchu, Taiwan, R.O.C. and the Department ofElectronic Engineering, Chung Yuan University, ChungLi, Taiwan, R.O.C.

K. F. Jea is with the Department of Computer Science, University ofWisconsin, Madison,WI53706.

D. W. Shieh is with the System Development Center, Institute for InformationIndustry, Taiwan, R.O.C.

hash functionwill becomemucheasiertousesincethe bother-some key collision problem can be avoided. There exist a numberof methodsfor the designofa one-to-one hash func-tion

[1], [3],

[8]-[10],

[22]

or called perfect hashing

func-tion in

[221.

In suitable situations their methods mayyield good hash functions as far as thememory space usedor the execution timeareconcerned.

In this paper an entirely newapproach isproposed for the design of

perfect

hash functions. An indicator table isused

in the construction of a perfect hash function with table

size in linear proportion to the number of keys. Compared

to other methods proposed in the literature for designing perfect hash functions

[1],

[3], [8]

-[101,

[22],

the

construc-tion procedures here have the advantages that they are easy

to

implement

and can be effectively applied to key sets of largesize.

The basic ideas employedinourconstructionarerehash and segmentation. In Sections II-IV we will show how random hash functions are organizedbyusingahashindicatortableto

construct a desired perfect hash function. Analytic resultsare

given

which

are

applicable

when problems sizesare small. In

Section V, twoalgorithmsaredesigned for the construction of the hash indicator table. Extensive experiments have been performed to testthenewapproach forproblems of largesize.

Theresults are presented in Section VI.

Formulas for calculating probabilities and expectations dis-cussedinthe context arelistedinthe Appendix.

II. RANDOM HASH FUNCTIONS

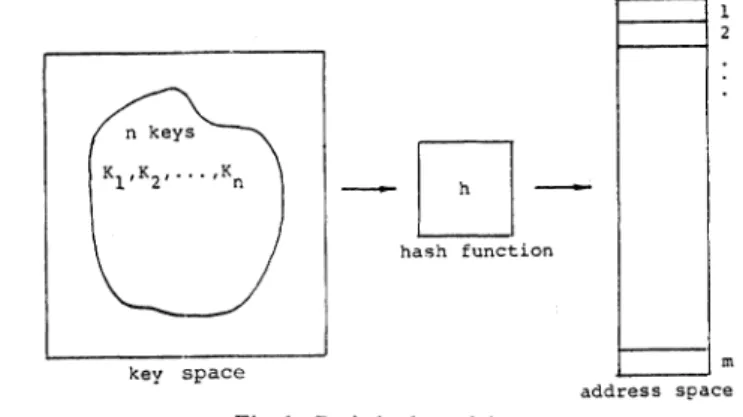
We shall consider random hash function first. Fig. 1 shows

the basic model which will be considered throughout this paper. In the model, a set of nnonequal

keysK,

,K2,*

,Kn

inthekeyspaceis mapped into anaddressspacewithmentries

Ih hash function 1 2 key space m address space Fig.1. Basic hashmodel.

by a hash function h. No interrelations will be assumedto exist among the n keys. The keys can be thought ofasjust arbitrary binary strings. Therefore, the hashfunction canbe

fully characterized by the listing of the values h

(Ki)

for all

1 .i.n, where 1

.h(Ki)<m.

h is called a random hash function whenever all theh

(Ki)'s

are selected randomly from

{

1, 2,

* m}

Wesaythatacollisionoccursif forsomei#

j,

h

(Ki)

=h

(K1).

In such situation, we also say that

Ki

and

K1

arecollided keys underh.

Definition 1: h is a perfect hash function iff no collision

occurs inh.

We define belowaprobability which will beused to measure

thelikelihoodof constructingperfect hashfunctions.

Definition 2: Let F be a set ofpossible distinct functions obtainable from a construction procedure P, with the

func-tions mapping from a set of keys into an address space. As-sume that there are

np

perfect hash functions amongthenF

functions inF. If ahashfunctionh isselectedrandomly from

F, the probability of h being perfect, denoted as pbp(h), is

equalto

np/nF-It should be noted that h is a formal name representing a

function selectedrandomly fromF inDefinition 2. Itcanalso bethought ofastheformalnamerepresentingafunction

con-structed by the procedure P. Clearly,

pbp(h)

depends entirely

onhowprocedure P constructsperfect hash functions. Asan example,assumethat his amapping functionselected randomly from

Fn Xm,

the set ofallfunctions thatmap nkeys into an address space with m entries. The chances that h is a

perfect hash function are ordinarily quite small. Actually,

pbp(h)=0

if

n>m,

and is

equal

to

m!/(m- n)!

X(1/ma)

if n < m. When n =m =10 pbp(h)=0.0003629. Even when

m is much larger than n, the probability is still very small.

Whenn=23 andm =365,wehavethefamous"birthday

para-dox"

[7],

[13]. The probabilityisonly0.4927,still less than

half!

We say that a hash function h has k singletons if thereare k entries in the address space with a single key hashed by h to each of them. Ingeneral, we canfindthe probability for

hhaving exactlyksingletons by thefollowing theorem. Theorem 1: Assume that h is arandom hashfunctionfrom n keysto anaddress space of size m. Let us denote the

proba-bility distribution of the number of singletons

k(O

< k < min

(m,

n)) asPk (n, m). Then

Pk(n,m)-=e(nm)

where

ek )n !mJ)nnk kLm kJ

(m-r-k)n-r-k

This theorem can be proved by first findingthe numberof

possible h functions having atleast

i

singletons,usingthe ordi-nary enumerator (xl +x2 +* +

Xmn)n

of the number of

ways in which n distinct objects can be distributed into m

distinct cells, then applying the principle of inclusion and exclusion [6], [14]

togetpk(n,m).

By using the distribution function in Theorem 1, closed

formfor the mean ofPk (n, m)canbe found

[41,

[I

1] as

E[k] =nX(1- (2)

Let us assumethat n=am, theformula n X (1 -

(lm))n-1

approaches nX e-° when n becomes very

large.

Therefore,

ish is selectedrandomly from

Fnxm,

ordinarily

it will be far from being aperfect hashfunction. To improvethis situation,

some information about the keys should be usedtoconstruct the hashfunction. In the next section we use rehashto con-struct a new hash function from a numberof hash functions selected from

Fnxm

. Information relatedtothekeysand the

hash functions selected is kept ina table called hashindicator

table(HIT).

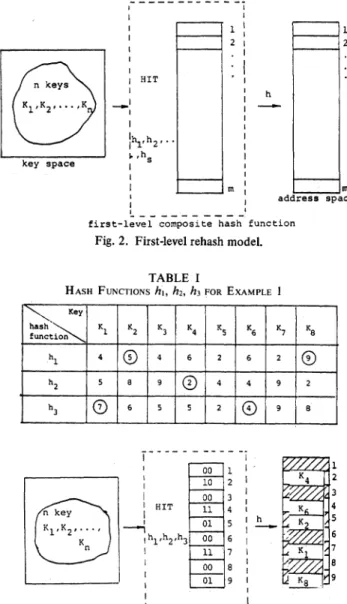
III. FIRST LEVEL REHASH

Fig. 2 shows the first-level rehash model where the hash function h is constructed from a number of hashfunctions,

hl,

h2,* * * ,

hs,

selectedrandomly from Fn

m,

Inthefigure,

the HIThas the same number ofentries asthatof theaddress

space. In fact, entry d in HITcorresponds to entry d inthe

addressspace.

The contents in HIT can be defined by thefollowing Pidgin Algolprogram.

Procedure1 [Procedureto ConstructFirst-Level

HIT]:

begin

KEYSET :={K1 K2

Kn};

clearallentiresofHIT; forj:= 1 step 1 untilsdo begin

forallelementsinKEYSET do

HIT(d) :=jif

HIT(d)

=0and

hj(Kr)

= d

foroneandonlyoneKrin KEYSET;

KEYSET KEYSET - {Kr

IKr

satisfiesthe above

conditions},

end end

The first-level compositehash function hcan be defined as

follows:

h(K)=hi(K)=d

if

HIT(hr(K))

$rforr<i

andHIT(h1(K))=

i,

=undefined otherwise. (3)

(1) It can be seen that if q hash functionsare selectedfor com-posingh,atable HIT ofwidth

[log2 (q

+

1)1

bits isrequired.

2-HIT t

1hi

h2 *t

I ~~~m

addx

first-level composite hash function

Fig. 2. First-level rehash model.

0. 6 1 2 o.51 0.4 0.31 0.2 0.1 0.C sm ress space TABLE I

HASH FUNCTIONs h1, h2, h3FOREXAMPLE 1

Key hash KI K2 K K4 K5 K6 K7 K functio~n 2 3 4 h1 | 4 ( 4 6 2 6 2 h2 |5 a 9 () 4 4 9 2 h3 6 5 5 2 9 8 KlI . . 00 1 I 10 2 00 3 HIT 11 4 01 5 h1th2,h3 00 6 11 7 00 8 . I 01 9 .L_ _ __ _ --_-__ K4 11- KS; , aK2 K ) K 1 2. 3 4 5 6 7 8 9

Fig. 3. HIT constructed by Procedure 1 ofExample1.

Tofindh(K)forakeyK in thekeyspace,weapplythehash

functions

hI,

h2,* *

*,h.

on K in turn until

HIT(hi(K))=i.

Ifthesearchfails, h(K) is undefined.

Example 1: Assume that the key setis{K1,K2,.* * ,K8},

and that the address space is from 1 to9. The hash functions

selected are

hl,

1h2,h3, as defined by Table I. Thecircles in

each row-h in the table indicate where the

hi

contributes

singletons.-The HIT constructed by Procedure 1 is given in Fig. 3. We can see thatK2 and K8 find their right places by

h,

. K4 by

h2,K1 and K6 byh3. Note that h2(

Q)

=5 is asingleton in

the second rowofh2, however, since5has been already

occu-pied by K2 through the mapping of

h,,

K1 doesnot find its

right position byh22. The mapping ofthe composedfunction hisundefinedontheremainingkeys K3,

Ks,

andK7.

Let us see how h(K6)can be calculated. When

h,,

h2, h3

are-applied on K6 in turn,wehave HIT(h1(K6))=HIT(6)=

(00)2 =0 1, HIT(h2(K6)) =HIT(4) =( )2 = 3 = 2, HIT

(h3(K6))-HIT(4)=(11)2 3 =3. Therefore, h(K6)=4.

Suppose that k'keys have been hashed successfully into the address space afters hash functions of

hj1's

are appliedin the

way described above. Givenany one keyK of thesekkeys, we can apply the

h,,

h2,* ,

h.

successively, consulting the

HIT table, to find h(K). We defineNE1- (n,m, s, k)as the

Qk(n,m)

s=7

s=3 s=1

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Fig.4. Distribution diagram of

Q9(n,

m) with n = 14, m =17, and s=1, 3,7.

expected number of times it is required to apply

hi's

for cal-culating h (K) with K amongthese k keys.

Let

Q'(n,

m) be the probability of getting k singletons by

applying

hI,

h2

,hs

in the way described previously,

where each

hi

maps from the n givenkeys to the address space of sizem. Formulas for calculating NE1 and

Qs

are givenin theAppendix.

Example 2: The

Qs(n,

m) values for n= 14, m = 17, s = 1,3,7, are calculated and plotted in Fig. 4.

It can be seen that Qj (n, m) is exactly the probability dis-tribution of the number ofsingletons of arandom hash func-tionand is equal to the distributionfunction Pk (n, m) in(1).

By comparing the values of Q (14, 17)with thoseof

Q'

(14, 17), one can observe that he may find more singletons in a

first-level composite hash function than in a random hash

function. The expectation ofk for Q)(14, 17)is 6.673471 while that forQk(14, 17)is 13.280872.

When n singletons have been obtained by the above con-struction, we get aperfect hash function. Theexpectation of the number oftimes ofapplying

hi's

in calculating h(K) is

NEl(14,

17, s,

14).

They are 1, 1.579916, 2.163818 with

s=1,3,7,respectively.

The probability of being perfect pbp for the first-level hash function composed from seven random hash function is

Q14(14,

17). It is much larger than

Q14(14,

17),the pbp of arandomhash function.

When more and more random hash functionsareselectedto compose a first-levelcomposite hash function,theprobability

ofbeing perfect of the composite function will becertainly

increased, but it will be increased very slowly. The reason isthat the more singletons wealready have, the fewerchances aretherefor theremaining keystobehashed onunused entries in the address space. It has been found that dividing the

address space into segments can be a more effective means to increasethe pbp than usingindefinitelymany randomhash

functions,aswillbedescribedinthe' next section.

IV. SECOND LEVEL REHASH

Fig. 5 showsthe second-levelrehash scheme.

The address spaceisdividedintoq segments. Corresponding

to segment

Ai,

which is ofsize

mi,

wehave a first-level com-posite hash function hi which maps

1K1,

K2, *

,K,}

into { 1, ,

mi}. HITi

isthe hash indicatortable of

h'

for indicat-ing which h isappliedtogetthevalueof

h'.

HIT1,,.

,HITq

compose the hashindicatortableHIT ofthesecond-level com-positehash functionH.

I,hl,...,hl l 2, 2 h1 hs HITI l

~

I

I,. ---I I HIT 2 q~~~~~~

second-level composite hash functionad

1 2 Al _ 1 2 A2 I1 I

.1

Aq . idress space

Fig.5. Second-levelrehash.

follows:

H(K)

=hj(K)

+ mt ifi, jcanbe found such that

t=O

HITi(hM

(K)) and

HITi(h'

(K)) :/rforr<j,and

HITa

(ha

(K)) / b fora<i,

1<b.s,

where it is assumed thatmo =0,

=undefined otherwise.

That is, if a keyK cannot find its right positionin the first segment by h, it will try the second segment by h2, and so

forth.

The following program is an implementation ofthe hash

functionH.

Procedure2

[Procedure

forComputing

H(K)J:

begin t :=0;

for i:= 1 step 1 untilqdo

begin

forj 1 step 1 untilsdo

begin

z

h(K);

if

HITi(z)

jthenreturnH(K) t+z

end; t:=t+m

end;

returnH(K) =undefined

end

We useR*(n, m, q)todenote theprobabilitydistribution of

getting k singletons by thesecond-level compositehash func-tion H. The vectormi is thepartitionontheaddressspace. It

can also be represented as

(mln,

m2,...*,

mq).

We shall also represent (mi ,m2,... in,.)asrm. qjm=mibyourconvention.

Formulas for calculating R'(n, mi, q) are also given in the

Appendix.

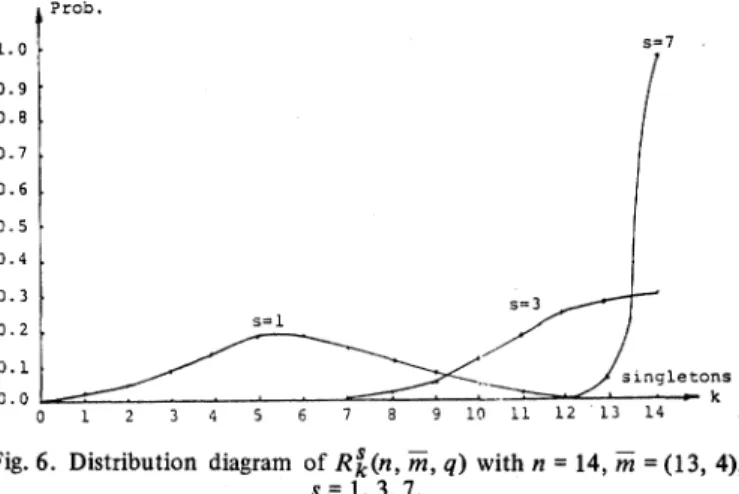
Example 3: To make things comparabletotheresults shown in Fig. 4, we let n =14,m =17,m =(13, 4),s= 1, 3, 7,and get three second-level composite hashfunctionswhichmap 14

keysintotwosegmentsofsize 13 and 4 each.

TheR'(n,

m,q)

values arecalculated andplottedonFig. 6.

Let usexamine the

Rk

(14, (13,4), 2)case. Theprobability 1.0 0.9 0.8 0.7 0.6 0.5 0.4 O. 3 0.2 0.] 0.0 ,Prob. s=l 1 27 f 4 5 7 89 101 1 13singletons 2 3 4 5 6 7 8 9 10 I11 12 13 14

Fig.6. Distribution diagram ofRs(n,rm,q) withn =14,m=(13,4),

s =1,3, 7.

for the second-level hashfunctionH to beperfect isR 4 (14, (13, 4), 2), which is greater than 97.8 percent!

Likein thefirst-levelanalysis,supposethat kkeyshave been

hashed successfully into the address space after the construc-tion of the second-level hash function. Given anyonekeyK

ofthese k keys, we canapply theh,h *,

h'5

h h h2* successively, consulting the second-level HIT table,to find H(K). Similarly, we define NE2(n, m, q, s,

k)

as the expected number oftimes it isrequired to apply

ht

's for

cal-culating H(K) with K among these k keys. Formulas for

calculatingNE2 are givenintheAppendix.

Example3 (Continued): NE2(n, mr,q,s,n)istheexpected

number of times to apply the

hj's

functionstocalculateH(K) for any keyK,ifthe second-level composite hash functionis

perfect. Using (A9) in the Appendix to calculateNE2(14,

(13, 4), 2, s, 14), we get 1.275607, 2.286545, 3.273526 for s= 1,3,7.

V. CONSTRUCTION OF THEHASH INDICATOR TABLE According to the way the hash indicator table is defined in

Section III, amultipass procedure canbedesignedforthe con-struction ofthe HIT. Let thetset ofkeys be {K1,K2, * ,

Kn}.

Assume that the partition of the address space

(Al,

A2,-*,Aq)

of size (M1, M2,

,mq)

and the hash

func-tions h *

*,

hlI

h * ,h , h,** h are allgiven.

Thefollowingis aHIT construction procedure.

Procedure3(StaticProcedureto ConstructHIT's):

begin

KEYSET ={K1,K2,

Kn};

clearallentriesofHITS; fori:= 1 step 1 until q do

for! 1 step 1 untilsdo

begin

forallelementsinKEYSET do

HITi

(d):=j

if

HIT1

(d)=0andh3(Kr)= d foroneandonlyoneKr in

KEYSET;

KEYSET := KEYSET -

{Kr

lKr

satisfies theabove

conditions};

end;

if KEYSET =empty then HITofaperfecthashfunction

hasbeen assigned elseitfailstofindaperfect hash

function

end

I

L

TABLE II

HASH FUNCTIONSFOREXAMPLE 4

Key fUncta

K1

K2

K3 K4 K5 K6 K7 K8 K9 h1 4 4 6 2 6 2 J 8 5 8 9 4 42 2

_D

h1 6 1 5 2 9 8 5 h2 1 3 2 4 2 3 2 5 3 2h2 4 5 2 5 5 1 3 h2₃ 5 2 (hC

1D3

4D

₂ HIT' 01 1 K9 1 t2102 K4 2 00 3 3 11 4, K 4 01 5 K2 5 006' 6 1 2 K1I77 008, H 9 9

~~~~~~~~~8

9 11 1 3 14 001 2 l2 1 I-, _ _ HIT lO 3 I-K 1 2 00 4 1 11 5' 1

Fig.7. HITconstructedbyProcedure 3 ofExample 4. Example 4: Assume that nine keysK1, K2, ,

Kg

are to

be hashed

perfectly

to an address space of size 14. The

ad-dress space is partitioned into

(Al,

A2)

of size

(9,

5).

The

hash functions used are {hL hh, h},

{h2, h2, h2}

asdefined by Table II. Again,as inExample 1,the circlesineachrowM

inthe tableindicatewhere theh contributessingletons. Fig.7 showsthe HITconstructedbyProcedure 3.

Procedure 3 works on an address space with the segments

preset to

(ml,*

* ,

mq).

In contrast to this, the size ofthe address space and the segments can be set in a dynamic man-ner, asthefollowingprocedure suggests.

Procedure4[Dynamic Procedureto ConstructHIT(or

H)]:

assume that the sizelimitation of the address space is m.

begin

KEYSET ={KK1,*, ;

for i = 1 step 1 until a large number M do begin

let

mi

be the size of KEYSET; m :=m-

mi;

if m <0, then it fails to find aperfecthash function, return;

reserve atableHIT1 of length

mi

and clear it; generate s hash functionshi, ,

h'

thatmap from KEYSET into

{1,

2,*

ri};

forj 1 step 1 until s do

begin

for allelements in KEYSET do

HITi

(d):=j if

HITi

(d)=0 and

hf

(Kr)=d foroneandonlyoneKr in KEYSET;

KEYSET := KEYSET {Kr Krwhichsatisfies the aboveconditions};

if KEYSET =empty thenHIT's of a perfect hash

function'has beenassigned,return end

end end

The expectation of the length of the HIT (or the

length

of the address

space)

andtheexpectationof thenumber of times it is required to apply

h(

'sto findH(K) for K=anykey K1,

with the HIT constructed by Procedure 4, are defined as L

(n,

s) and NED(n,

s)

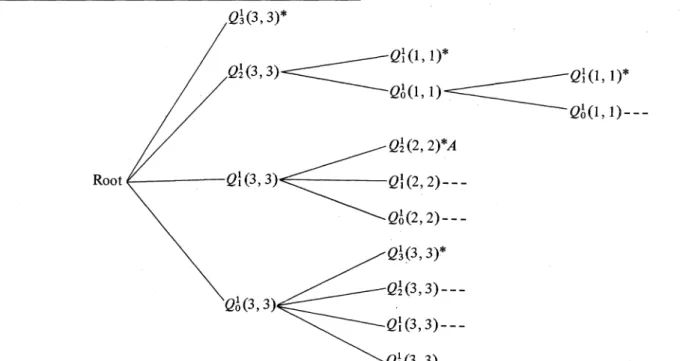
respectively. They can be calculated by formulasintheAppendix.

Example 5: Let 's=1,n =3. The probabilities ofall

possi-ble cases constructed by Procedure 4 are depicted by the following probabilitytree:

W(3,

3)*

Q'(3,

~

3) Q(l,~) Q1(1, 1)*

,Q2(3,3)=X~~~Q

(11

1)*

Q1~~~~~~~Q

(1,

1)

Q'(2,

2)*A

Q'

(3, 3) Ql(2,

2)-__

-

Qo(2,

2)---Ql(3,

3)*

/,-J

jl-t

-v\-(3,

3)---Root

The pathfrom theroot to each terminal node(indicated by

an asterisk) represents a

possible configuration

(11.,

q4,),

with

11

+12 + +4,=3. For example, the path from the root to *A in the figure represents the configuration (1, 2).

The probability to get 11 = 1, 12 = 2 isQI(3, 3)X Q (2,

2)-the product ofthe Qh onthepathfrom theroot to

the-termi-nal node.

There are 33 =27 distinct functions which map three keys

into {1, 2, 3}. Six of these contain 3

singletons,

18 of these contain 1 singletons, and 3 of these contain 0

singletons.

Therefore,

Ql(3,

3)

=

6/27

=

2/9, Q (3, 3)

=

0,

Ql(3,

3)

=

18/27

=

2/3,

Q%(3, 3)

=

3/27

=

1/9.

Similarly,

Ql

(2, 2)

=

1/2,

Q1(2,

2)

=

0, Q (2, 2)

=

1/2.

The

probability

tree canbe

sim-plifled to the following tree by noting that

Ql

(3, 3)

=0 and

Ql

(2,

2)

0: 2* 9 / ~~~~~1* 6 2 2* V Root 1 6 9 9 9 By

(A6)

wehave

L(3, 1)= 2

X 3+ X - X

(3+2)

+ 2 X (3

+2+2)+

* +4X

2X(3+3)+

4 X X

X(3

+3

+2)+*.

+ I X g

X2g

X

(3

+3

+3)

+** 9 9 9 6

38

Similarly,

by

(A8),

wehave

NED(3,1)

=9 X +

69

XIX

[ X(1+2 X2)] + + -₉ X 2₉₃X [ +

3]

+4X 6 X X

[

+ X

(1

+2X

2)]

+4X X 2 X [I +1 + 3] +

=

241

8-VI. EXPERIMENTAL RESULTS

The formulas derived in theprevious sections can beusedto

find

important measures to characterize the construction of

second-level perfect hash functions. However, they can be

applied only when the problem sizes are small. Thisis due to

the fact that the formulasget involved with the enumeration of all possible partitions of a number ofintegers. The

com-plexity of such enumeration is exponential. Computing by recursiveformulaseasesthe problem to a certain extent. When the integers (parameters) becomes larger, it will be still ex-tremely time-consuming to do the calculations. For instance, it takes 36.237 s for a program implemented on a Cyber

170/720 system to calculate NE2(14, (14, 3), 2, 7, 14) = 3.273526. Therefore, extensive experiments have been de-signed to test the approach of constructingperfecthash func-tionsintroduced inthispaper.

Quite a number ofstrategies can be adopted for the parti-tioning of a given address into segments in the experiments.

Here we introduce a strategycalledgeometric partition strategy.

9

Assume that the size of the address space is m, and that it is tobepartitioned into segment

(m

I1

,M2, * Inthegeometric partition strategy all m

I-/mi

are kept close to a constant,

called the reductionratio. If thereductionratiois

'y,

0 'yc 1,

thefollowing formulacanbeapplied.

ml llzm

21

MEn=ALx

m,1

+

I-

if

>L

i.m

j=1 i-I =m- L mi 1=1 otherwise. (4)

For example, if m= 125, y=

0.3,

m will be partitioned into 5 segments according to the geometric partition strategy as

(mi , M2,M3

,iM4

,in5)=

(88,

26, 8,2, 1).

In all the experiments, 36-bitrandom numbersaregenerated

for thekey values. The hash functions

hi's

arealso generated randomly.

Some more comments on the commonly used

terminology,

loading factor, are needed here. In an experiment, if the

numberofkeysis n, the loading factor is given as r,thenthe

pbp 1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.0 L 0.0 Fig. 8. T0O. 5 .11 TE - .6 T-0.8 T=0. -0.9~ ~ ~~~ 0 reduction _ ratioy 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

Diagramof thepbpvalues ofExperiment1. Experiment 1-Explanation:

1)

Geometricpartition strategy is tested.

2)

Reduction ratio y varies from 0.1 to0.8 instepsof 0.1.

3)

Loadingfactorrvariesfrom 0.5to0.9instepsof0.1.

4)

Numberofrandomhashfunctions for eachh' is7.

5)

100independent setswith 100 nonequal keysineachare

tested for eachcombinationofyand r.

6)

For each combination ofyand r, wecalculatethe proba-bility of being perfect pbp asthe number ofsucceeded trials

dividedby the numberof total trials

(which

is 100).

Theresultsof this experiment areplottedinFig.8.

From Fig. 8 we may observe immediately thatwe mayhave better chancetofindaperfect hash function when the loading factor is smaller, which is quite natural. Also, all the curves

corresponding to different T valuesappear concave downward. It appears that there exists one andonly one peak in each of

thesecurves.

Experiment2-Explanation:

1)

Dynamicprocedure

(Procedure 4)

for the constructionof

aperfect hash functionistested.

2)

Number of keys n varies from 40 to 50, in stepsof 1,

thenfrom 50to500 in stepsof50.

3)

For each n, 100 independent sets withn nonequal keys aretested.

4)

The number ofhash functionsfor constructing eachhiis

1,3,7,i.e.,s 1,3,7.

The results ofExperiment 2 are depicted in Figs.9 and 10.

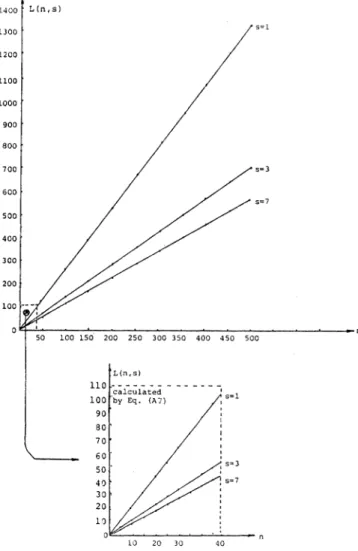
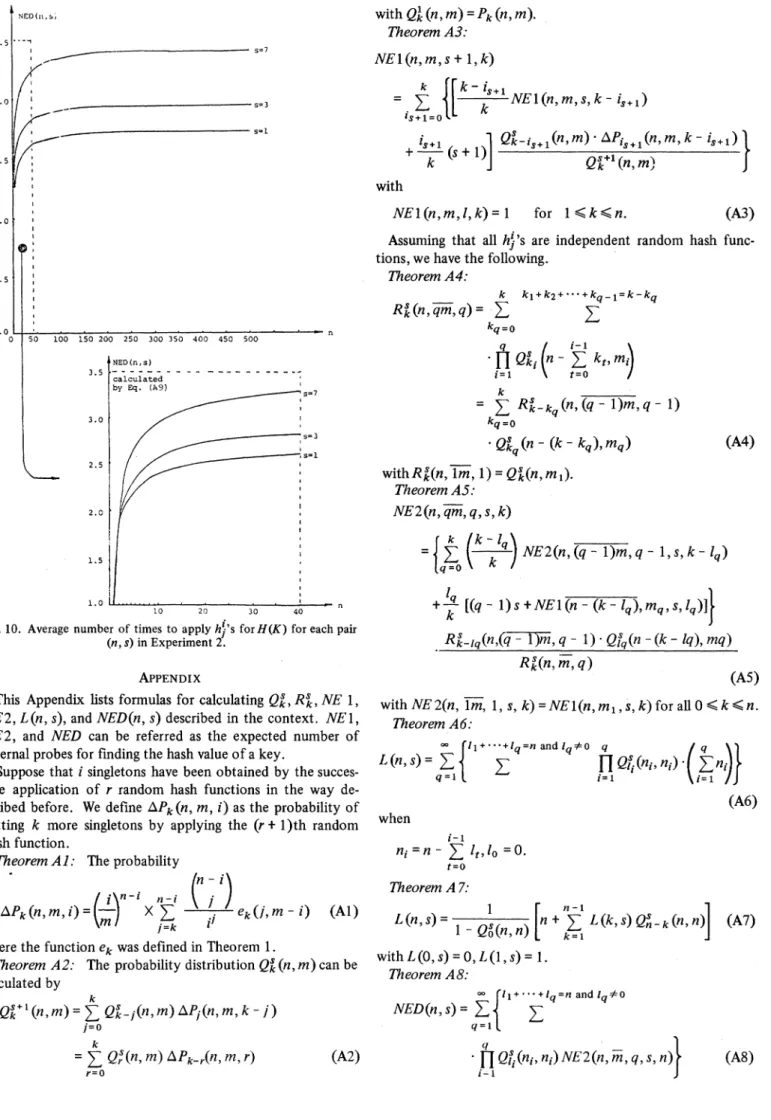
Fig. 9 shows the average size of the address spaceassigned for

each

(n, s)

in the experiment. Note that there are 100 trials for each combination ofn and s. Fig. 10 shows the average number of times to apply

ha's

for calculating

H(K)

for each

combination ofnands. Forn<40,thesetwofigures,L

(n, s)

and

NED(n, s),

arecalculated

through

applying

(A7)

and

(A9),

respectively.

Example 6: Suppose that Procedure 4will be usedto con-struct a perfect hash function tomap 300nonequal keysinto an address space. FromFigs. 9 and 10,if 7 hashfunctionsare used in constructing each hi, the length ofthe address space will be about equal to 348. Thetotal size of the HIT table

L(n, s)

s=7

500

10 20 30 40

Fig.9. The average size of the address space assigned for each pair (n, s)inExperiment2.

created will be about 348 X 3 bits. Whichisabout 131 bytes.

The expected number oftimes it isrequired to apply

hM's

for

calculatingH(K) willbe about equalto3.48. VII. DISCUSSION

Thispaperessentially proposedtwoprocedures for construct-ing perfect hashfunctions. In thefirstprocedure, the segmen-tationof the address space is preset. From Experiment 1 we can see that the way the address space ispartitionedhasgreat

effect on the probability that a perfect hash function can be

obtained. An interesting but unsolvedproblemistoshow how to partition the address space so that we may maximizethe probability ofobtaining a perfect hash functionby the con-structionprocedure.

In the second procedure, the segmentation ofthe address spaceisobtained

dynamically.

If the address space isunlimited,

the procedure can certainlyconstruct a perfect hash function eventually. From Experiment 2, we observe that the ratioof

the size of the address space constructed to the number of keys will approach a constant for each s value, as the number ofkeys goeslarge. Forexample, when s=7, L(n, s) - 7/6n.

This provides us a very simple guide rule in applying Proce-dure 4.

3.5 3.0 2.5 - s=7 s-.1 withQ4(n,m)=Pk (n, m). Theorem A3: NEI(n,m, s+ 1,k) -1s0{[ k NE1(n,m,s,k-

is+1)

1s+1=0

+s+l

1)Qk-s+

I

(n,

m)

APis+1(n,m,k-

iS+,)

w k J Qk (n,m) with 2.0 1. 5 1.0 NEl(n,m,l,k)= I for 1.k<n. 50 100 150 200 250 300 350 400 450 500 NED(n,s) 3.5 - -- - -- - - - --calculated by Eq. (A9) 3.0 2.5 2.0 1.5 -s=3 I= is 1 .0-I| 10 20 30 40

Fig. 10. Average number of timestoapply h's for H(K)for eac (n,s)inExperiment 2.

APPENDIX

This Appendix lists formulas for calculating Qk,

R4,

A

NE2,

L(n, s),

and NED(n, s) described in the context. . NE2, and NED can be referred as the expected numb

internal probesforfindingthe hash value of a key.

Suppose that isingletons have been obtained by the su sive application of r random hash functions in the wa,

scribed before. We define

APk

(n,m, i) asthe probabili getting k more singletons by applying the (r+

I)th

rar hashfunction.

Theorem Al: The probability

APk(n,

m,

i)

X ( / ) eke (

j=k

where the functionek wasdefined inTheorem 1.

Theorem A2: The probabilitydistribution Qk(n,m) Cz

calculated by k

Q

k+

(n,m)

=

f,

Qs

-j(n,

m),APj(n,

m,k-

j)

j=0 k = Z

Q'(n,

m)

APk..r(n,

m, r) r=o (A3) Assuming that all

hj's

are independent random hash

func-tions, wehavethefollowing. TheoremA4: k kl+k2+"--+kq l=k-kq

Rs(n,qm,q)=

Z kq=o *

1Qsin

kt, m,

z=1 ~t=O k Z

Rs-

kq (n, (q-

I)m,

q - 1) kq=O

Qs

(n

-

(k

-

kq),

mq)

(A4)

withR(n,lm, 1)s Q(n,mi1). TheoremAS:

NE2(n,qm,q,s,k)

k ( k

k-

NE2(n,

(q

-

1)m,

q- 1,s,k- I

)

q =o. +

k[(q

1)

s+NE 1

(n

-

(k

-

14),

mq,

s,

1qB)]}

Rs-lq(n,(ql7JTm,

q - 1)

Qsq(n

-(k -

lq),

mq) R (n,rm,q) (AS)

with NE2(n,Ilm, 1,

s,

k)=NE1(n

Ml,

s, k) for all O< k6n.

Theorem A6:

00 Il) +.+lXq=nandIq*1Oqzq)}

L

(n,s)= f<

I

I

Qls

(ni,

ni)

in),F

(A6)

when ni=n- Z t,lo =0. t=o TheoremA7: (Al)

L(n, s)=

QS( n)[n

E

(

L(ks)Qn-k(knln)]

anbe

withL(0,s)

=O,L(1,s) = 1. TheoremA8: 00 rl+. +lq=nandlq*O NED(n,s)= I q=1

(A2)~~~~~f

Qs

Q(ni,

ni) NE2(n,

m-,

q, s,

n)}

(A7)

(A8)

n

where f-i

ni=n-

It,lo=0,

and M

=(nl,fn2,**,fnq).

t=o TheoremA9: NED

(n, s)

= I I

Qo(n,

n) *s

*Qos(n,

n)

+

NEI1(n,

n, s,

n)

Qns(n,

n)

+ nL

[(

)NE1

(n,

n, s,

k)

+

(n

-

k)

(s

+NED

(n

-

k,

s))]

*Qk(n n)

(A9)

REFERENCES

[1] M. R. Anderson and M. G. Anderson, "Comments on perfect hashing functions: A single probe retrieving method for static sets," Commun.Ass.Comput. Mach.,vol.22,p.104, Feb. 1979. [2] W. Buchholz, "File organization and addressing," IBM Syst.J.,

vol.2, pp.86-111, June 1963.

[3] R. J. Cichelli, "Minimal perfect hash functions made simple," Commun.Ass.Comput.Mach., voL 23, pp. 17-19, Jan. 1980.

[41 F. N.Davis and D. E.Barton,Combinational Chances. London: Griffn, 1962.

[5] M. W. Du, K. F. Jea, and D. W. Shieh,"The study of new perfect hash schemes," inProc. COMPSAC'80, Chicago, IL, Oct. 1980, pp.341-347.

[6] M.W. Du and H. C.Lin,"Thedesign of a memory savingChinese

input/output system," in Proc. NCS, Taipei, Dec. 1979, pp. 8.1-8.10.

[7] W. Feller,AnIntroductiontoProbability Theory and Its Appli-cations,vol.1. New York:Wiley,1950.

[8] S.P.Ghosh,DataBaseOrganizationfor DataManagement. New York:Academic, 1977.

[9] G. Jaeschke and G. Osterburg, "On Chichelli's minimalperfect

hashfunctionsmethod," Commun.Ass. Comput. Mach.,vol.23, pp.728-729,Dec.1980.

[10] G. Jaeschke, "Reciprocalhashing: A method forgenerating mini-mal perfect hashing functions," Commun. Ass. Comput.Mach.,

vol.24, pp.829-833, Dec. 1981.

[11] K. F. Jea, "The study ofthe staticpropertiesofa newperfect hash scheme," Master thesis, Nat. Chiao Tung Univ., Hsinchu, Taiwan,R.O.C., May1980.

[12] L. R. Johnson, "An indirectchaining method foraddressing on secondarykeys,"Commun.Ass.Comput. Mach.,vol.4, pp. 218-222, May1981.

[13] D. E.Knuth, TheArtofComputerProgramming, Vol. 3,Sorting andSearching. Reading,MA:Addison-Wesley,1973.

[14] C. L. Liu, Introduction to Combinatorial Mathematic. New York: McGraw-Hill, 1968.

[15] V. Y. Lum, P.S.T. Yuen, and M. Dodd, "Key-to-address trans-form techniques: A fundamental performance study on large existing formatted files,"Commun.Ass.Comput. Mach.,vol. 14, pp.228-239,Apr.1971.

[16] W. D. Maurer and T. G. Lewis, "Hash table method," Comput. Surveys,vol.7, pp.5-19,Mar.1975.

[17] R.Morris,"Scatter storagetechniques," Commun.Ass. Comput. Mach.,vol. 1, pp.38-44,Jan. 1968.

[18] C. A. Olson, "Random access file organization for indirectly accessed records," inProc. ACM 24th Nat. Conf., 1969, pp. 539-549.

[19] W. W.Peterson, "Addressing forrandom-access storage," IBMJ. Res.Develop.,vol. 1, pp.130-146,Apr. 1957.

[20] G. Schay and W. G.Spruth,"Analysis of a file addressing method," Commun.Ass. Comput. Mach.,vol. 5, pp.459-462,Aug. 1962. [21] D. G. Severance, "Identifier search mechanisms: A survey and

generalized

model," Comput.

Surveys,vol.6,pp. 175-194,

Sept.

1974.

[22] R.Sprugnoli, "Perfecthashingfunctions: A single probe retriev-ing method for staticsets,"Commun.Ass. Comput. Mach.,vol. 20,pp.

841-850,

Nov.1977.

[23] M.Tainiter,"Addressingforrandom-access storage withmultiple bucket capacities,"J.Ass. Comput. Mach.,vol.10,pp.

307-315,

July1963.

M. W. Du (S'70-M'72) received the B.S.E.E. degree from the National Taiwan University in 1966 and the Ph.D.

degree

from TheJohns

Hopkins University, Baltimore, MD,in1972. He is currently the Director of the Institute ofComputer

Engineering,

National ChiaoTung University, Hsinchu, Taiwan. His research in-terestsincludefaultdiagnosis,automata

theory,

algorithm design andanalysis, database

design,

andChineseI/0design.

T. M.Hsieh wasborn inTaiwan, onNovember

15, 1947. He received the B.S.degreein elec-trical engineeringfrom theChungYuan Univer-f

2 _Fg0:'t$! | slsity, Chung-Li, Taiwan, in 1970 and the M.S. degree in electrical engineering fromthe Insti-tute of Electronics, National ChiaoTung Uni-versity, Hsinchu, Taiwan, in 1974.

He isnowworkingtowards the Ph.D. degree in the Institute of Electronics, National Chiao Tung University. He previously worked for Telecommunication Laboratories, Chung-Li,

Taiwan, before joining the Department ofElectronic Engineering at theChungYuanUniversity in 1975,where he iscurrentlyanAssociate Professor. His research interests include database systems, fault-tolerantcomputing,microprocessor/microcomputer basedsystems.

K.F. Jeawasborn inTaiwanonMay 13,1956.

Hereceived the B.S. and M.S. degreesin

com-puter science from the National Chiao Tung University, Hsinchu, Taiwan, in 1978 and 1980, respectively.

From 1977to 1980, he servedas aResearch Assistant in the Department ofComputer Sci-ence, National Chiao Tung University. He is

currently working towardsthe Ph.D.degreein computer science at theUniversityof Wisconsin, Madison. His research interests include data-base design,programminglanguageandcompiler design,algorithm de-sign,andanalysis.

D. W. Shieh was born in Taiwan, Republic of China, on January 1, 1952. He received the B.S. andM.S.degrees in computer science from theNationalTung University,Taiwan,Republic ofChina,in1976 and1980,respectively.

Currently, he isaSystemEngineerat the Sys-temDevelopmentCenter,Institute for Informa-tionIndustry, Taiwan, Republic of China. His primaryjobissoftware systemdevelopment.