Strictly Nonblocking
f-Cast Log
d
(N; m; p) Networks
Frank K. Hwang, Yang Wang, and Jinzhi Tan
Abstract—Necessary and sufficient conditions for Logd(N; m; p) network to be point-to-point strictly nonblocking are known. Re-cently, Kabacinski and Danilewicz obtained necessary and sufficient conditions for the Log2(N; 0; p) network to be broadcast strictly nonblocking. In this paper, we give necessary and sufficient conditions for Logd(N; m; p) to be f-cast strictly nonblocking for everyf, thus covering the point-to-point case (f = 1) and the broadcast case(f = N) as special cases.
Index Terms— -cast, broadcast, strictly nonblocking.
I. INTRODUCTION
L
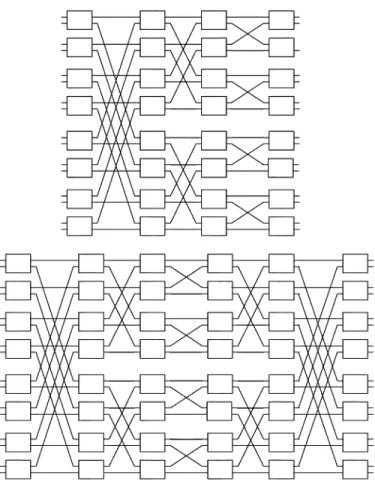
EA [1] first introduced the Log network which has inputs and outputs and stages. The first (input) stage has crossbars, the last (output) stage has crossbars, and the inner stages consist of copies of an -stage inverse banyan network , where each input (output) crossbar is connected to every copy of . (See Fig. 1 for an example of .)Shyy and Lea [2] extended this network to Log
by replacing in the middle with -extra-stage inverse banyan networks where the connection pattern of the extra stages is a mirror reflection of the first stages of the inverse banyan network. (See Fig. 1 for an example of , Fig. 2 for an example of
Log .) Note that Log is the Cantor
net-work [3] with copies of the Benes network [4] in the middle. The Log network can further be extended to the Log network by using -ary crossbars. (See Fig. 3 for an example of Log .)
Nonblocking networks are favorable in designing switching networks, since a conflict-free path is available for any pair of idle input and output. There are several kinds of nonblocking-ness. Strictly nonblocking means that any pair of idle input and output in a network can be connected regardless of the existing connections of other pairs in the network (all connecting paths must be link disjoint).
Hwang [5] extended a result of Shyy and Lea from binary to -ary, as follows.
Paper approved by A. Pattavina, the Editor for Switching Architecture Perfor-mance of the IEEE Communications Society. Manuscript received September 1, 2005; revised March 3, 2006 and August 3, 2006.
F. K. Hwang is with the Department of Applied Mathematics, National Chiaotung University, Hsinchu 30050, Taiwan, R.O.C. (e-mail: fhwang@ math.nctu.edu.tw).
Y. Wang is with the Computer Science and Engineering Department, State University of New York at Buffalo, Buffalo, NY 14260-2000 USA (e-mail: yw43@cse.buffalo.edu).
J. Tan is with the College of Mathematics and Information Science, Wenzhou University, Wenzhou 325035, China (e-mail: tanjz@126.com).
Digital Object Identifier 10.1109/TCOMM.2007.896055
Fig. 1. BY (4; 0) and BY (4; 2).
Theorem 1: The sufficient condition for Log to be point-to-point strictly nonblocking is
A careful examination shows that the worst-case scenario as-sumed in the proof of the theorem can be realized. So the con-dition in Theorem 1 is also necessary.
Lea mentioned that his argument for the point-to-point network can also apply to multicast traffic. Tscha and Lee [6] gave necessary and sufficient conditions for Log to be multicast strictly nonblocking, but the result is really for wide-sense nonblocking, since a special routing algorithm is used. Kabacinski and Danilewicz [7] gave the following result.
Theorem 2: The necessary and sufficient conditions for Log to be broadcast strictly nonblocking are
.
To clarify our terminology, -cast means an input can request to be connected to at most outputs. When is unspecified, we use the general term multicast. When , i.e, is uncon-strained, then we use the term broadcast.
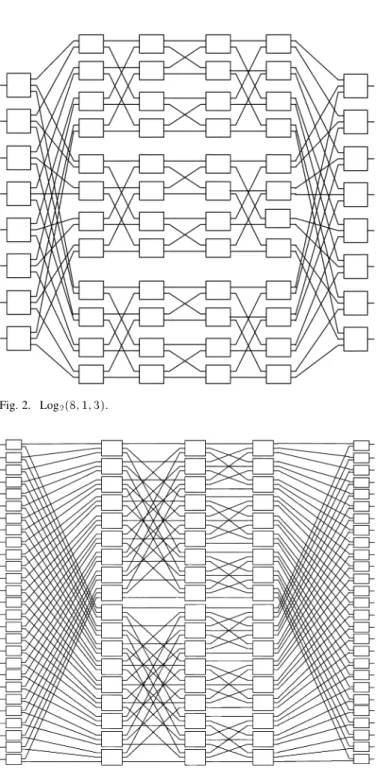
Fig. 2. Log (8; 1; 3).
Fig. 3. Log (27; 0; 2).
In this paper, we give necessary and sufficient conditions for Log to be -cast strictly nonblocking for all , thus generalizing Theorem 2 in three directions: 1) from binary net-work to -ary netnet-work; 2) from no extra stage to extra stages; and 3) from to general . Our strategy is to deal with the case first in Section II, and then extend the result to the general case in Section III. We summarize our findings in Section IV.
II. LOG
Consider a request from input to output . Then the channel graph is simply the path from to consisting of
links . A path from to is called
the set of -intersecting outputs; the set of -marginal outputs.
Let denote the cardinality of the set . Note that in the
Log network, , , and
Take Log as an example to explain the preceding definitions. Since Log contains three identical copies of in the middle, we will only use one middle copy to illustrate the concepts. In Fig. 4, suppose the request to be connected is from input 0 to output 0. Then,
, , ,
,
, , ,
. , ,
, , , ,
, Request generates a
1-in-tersecting path, request generates a 4-intersecting path.
Lemma 3: If , then .
Proof:
Theorem 4: Log is -cast strictly nonblocking for if and only if
Proof: Suppose the current request involves outputs. Since we can connect the outputs independently one by one, we may assume . Let the current request be . Note that previous connections from cannot block since they can share links. Therefore, these connections will be ignored in the counting of intersecting paths.
Fig. 4. BY (5; 0).
Suppose . The upper bound implies
for Hence
which implies that there are always enough outputs in to receive requests from . Thus the maximum number of -in-tersecting paths is just .
By Lemma 3, the lower bound implies
i.e., the combined -marginal and -marginal inputs can use up all remaining outputs. Hence there is no need to count intersecting paths beyond . Note that it does not matter whether alone can use up all of , since in either case there is a total of paths intersecting and . Thus the total number of intersecting paths is
This maximum can be achieved since the proof assures the availability of inputs and outputs for all the intersecting paths counted (just make out a request frame according to the de-scription given in the proof).
Again use as an example. When ,
con-sider requests , , which will use
15 copies. When , consider requests ,
, , which will use 12 copies.
When , consider requests , ,
, , , which will use 9
copies.
Setting and ,
respectively, in Theorem 4, we obtain the following.
Corollary 5: Log is broadcast strictly nonblocking
if and only if .
Corollary 6: Log is point-to-point strictly
non-blocking if and only if .
These two results are, of course, known in the literature, in [5] and [7].
III. LOG
We now study the general extra stages case.
Theorem 7: Log is -cast strictly nonblocking if and only if the equation shown at the bottom of the page holds true. if if if if if
Fig. 5. Channel graph of Log (8; 1; 3).
Proof: Again, we may assume that the current request is
point-to-point and from input to output . For , the
channel graph has stage- and stage- links
in every middle copy. Hence it takes -intersecting paths to block the channel graph of one middle copy (see Fig. 5). Using an argument of Shyy and Lea [2], each -intersecting path blocks only portion of the channel graph of the middle copy, or blocks copy of the Log network. For , the channel graph of every middle copy has links; hence each -intersecting path blocks copy. Let be the set of all inputs except , and all outputs except . Notice that an intersecting path originated from , , can arrive at every output of . Similarly, any
intersecting path to , , can start from
any input of . Furthermore, requests from , or to , , can block copy, as mentioned above. In the worst case, requests from or to will take pri-ority over connections from , or to for
, since they have stronger blocking ability. In the
Log network, we have , for ,
and , for if if if if Note that for
We proceed by counting intersecting paths in the order and
, and , and , , ,
, and stop whenever the counted intersecting paths have used up the remaining outputs. The proof is partitioned into cases depending on when the remaining outputs are used up.
1)
copies. The remaining outputs will be used up by requests
from or to , each such intersecting
path blocks copy. Therefore, the total number of blocked copies is
3) .
The upper bound and the lower bound are equivalent to
Hence, the requests from and to cannot use up , but the requests from can overflow from to . Further
Hence there is no need to count beyond stage . Thus the total number of blocked copies is
4) .
The upper bound is equivalent to
Hence, requests from do not overflow to . The lower bound implies that, by setting and
in Lemma 3
i.e., all outputs available at step will be used up by the next step. Again, it does not matter whether they are
if if if
Fig. 6. BY (3; 1).
used up at step . Thus the total number of blocked copies is
5) , .
The middle stages consist of copies of
, which we will refer to as the reduced inverse banyan net-works. The upper bound of says that the outputs of these re-duced inverse banyan networks are intact, i.e., none of them is used by requests from . Hence, we can apply Theorem 4 with replaced by everywhere. Note that for stage in a re-duced inverse banyan network
which are times of a normal . However, to
block a copy of takes the blocking of copies of the reduced inverse banyan networks. So the net effect of blocking in the reduced inverse banyan network is same as in
the normal , and Theorem 4 applies.
Again, the worst case described above can be achieved, since the description in the proof assures the availability of the inputs and outputs counted in the intersecting paths.
Note that in the first three cases, outputs in are used up. In the last two cases, may not be used up by , but are not
available for .
Let us take Fig. 6 as an example to see the concept of over-flow. In the figure, we have , , . Setting , then it is the third case, that is, requests from and to cannot use up , but requests from can overflow from to . In the figure, input 1 generates requests to outputs
, which include one output of .
Again, setting and , respectively, we obtain the following.
Corollary 8: Log is broadcast strictly
non-blocking if and only if .
Corollary 9: Log is point-to-point strictly non-blocking if and only if
Setting , we obtain the following.
Corollary 10: The -ary Cantor network is -cast strictly nonblocking if and only if the equation shown at the top of the page holds true.
IV. CONCLUSION
Recently, Kabacinski and Danilewicz gave necessary and suf-ficient conditions for Log to be broadcast strictly non-blocking. We extended it to Log . Further, we ob-tained the surprising result that the conditions are independent of (Corollary 8).
Bassalygo and Pinsker [8] proved that a strictly nonblocking broadcast network contains at least crosspoints, not fewer than those of an crossbar. Thus the only hope is to construct efficient -cast strictly nonblocking networks.
We gave necessary and sufficient conditions for Log to be -cast strictly nonblocking for every , thus containing the point-to-point and broadcast as special cases. Note that the number of copies of in the middle decreases rapidly with . For example, the number is for , and is the minimum integer larger than
for . In particular, we obtain necessary and sufficient conditions for the Cantor network, i.e., Log , to be -cast strictly nonblocking. Though we get the strictly non-blocking condition as above, it only guarantees the existence of a path. How to find it efficiently is still an issue, and we will take it for future research.
REFERENCES
[1] C.-T. Lea, “Multi-log N networks and their applications in high-speed electronic and photonic switching systems,” IEEE Trans. Commun., vol. 38, no. 10, pp. 1740–1749, Oct. 1990.
[2] D.-J. Shyy and C.-T. Lea, “log (N; m; p) strictly nonblocking net-works,” IEEE Trans. Commun., vol. 39, no. 10, pp. 1502–1510, Oct. 1991.
[3] D. G. Cantor, “On non-blocking switching networks,” Networks, vol. 1, pp. 367–377, 1971–1972.
[4] V. E. Beneˇs, “Mathematical theory of connecting networks and telephone traffic,” in Mathematics in Science and Engineering. New York: Academic, 1965, vol. 17.
[5] F. Hwang, “Choosing the bestlog (N; m; P ) strictly nonblocking networks,” IEEE Trans. Commun., vol. 46, no. 4, pp. 454–455, Apr. 1998.
[6] Y. Tscha and K. Lee, “Yet another result on multi-log N networks,”
written or coauthored the following books: The
Steiner Tree Problem (Amsterdam, The Netherlands:
North-Holland, 1992); Combinatorial Group Testing
and Its Applications (Singapore: World Scientific, 1993, 2nd edition, 2000); The Mathematical Theory of Nonblocking Switching Networks (Singapore:
World Scientific, 1998); and Reliabilities of Consecutive-k Systems (Norwell, MA: Kluwer, 2000).
research from Zhejiang University, Zhejiang, China, in 1991 and 2005, respectively.
She is currently with the College of Mathematics and Information Science, Wenzhou University, Wen-zhou, China. Her research interests include the field of combinatorial optimization.