Electrophoretic Mobility of a Spherical Particle in a Spherical Cavity

JOURNAL OF COLLOID AND INTERFACE SCIENCE196, 316 – 320 ( 1997 ) ARTICLE NO.CS975220

NOTE

Electrophoretic Mobility of a Spherical Particle in a Spherical Cavity

where Ç2 _{is the Laplace operator, r the space charge density, e the}

permittivity of the liquid phase, N the number of ionic species, zjand

The electrophoretic mobility U of a spherical particle in a

n0

j the valence and bulk concentration of ion species j , respectively, e

spherical cavity for the case of low electric field is estimated

the elementary charge, and k and T the Boltzmann constant and absolute

for an arbitrary thick electrical double layer. We show that if

temperature, respectively. Following Zydney’s treatment ( 1 ) , F is

de-the particle is uncharged and de-the cavity negatively charged,

composed into F1and F2. The former denotes the electrical potential the deviation in the mobility based on the linearized Poisson –

distribution in the absence of the applied electric field, and the latter,

Boltzmann equation, UL, can be serious even at a low electrical _{the potential distribution outside the particle due to the presence of the}

potential. In this case, the variation of the absolute deviation, _{electric field. Suppose that the surface potentials of particle and cavity}

ÉU0 ULÉas a function of ka , k and a being, respectively, the _{are fixed at F}

aand Fb, respectively. Then, we have ( 1 )

reciprocal Debye length and particle radius, has a maximum. The ka at which the maximal absolute deviation occurs

in-creases with l ( particle size / cavity size ) , and the maximal ab- Ç2_F

1Å 0

∑

N

j Å1

zjen0jexp (0zjeF1/ kT )

e , [ 2 ]

solute deviation decreases with l. The latter increases with the

absolute surface potential of cavity. If the particle is positively Ç2_F

2Å0, [ 3 ]

charged and the cavity uncharged, UL is sufficiently accurate

FÅF1/F2, [ 4 ]

if the electrical potential is low. q 1997 Academic Press

Key Words: electrophoresis; spherical particle; spherical cavity; F1ÅFaat rÅa and F1ÅFbat rÅb [ 5 ]

boundary effects.

ÌF1

Ìu Å ÌF2

Ìu Å0 at uÅ0 and uÅp. [ 6 ]

The last expression implies that F1and F2are symmetric about the z axis. INTRODUCTION

The flow field is governed by the Navier – Stokes equation ( 1 ) In a recent study, Zydney ( 1 ) analyzed the electrophoretic behavior of

a spherical particle in a spherical cavity under the condition that Henry’s _{Ç r£ Å0, [ 7 ]}

law ( 2 ) is applicable; i.e., the applied electric field is weak so that the

hÇ2

vÅ Çp/rÇF, [ 8 ]

distortion of the ion cloud surrounding the particle is negligible, and the disturbance in electrical potential distribution due to fluid flow is

insignifi-cant. The model proposed is applicable to an arbitrary thick electrical double _{where v is the fluid velocity,Çthe gradient operator, p the pressure, and} layer at low electrical potentials. Although the system under consideration _{h the fluid viscosity. Here, the particle moves with velocity U in the z} is essentially imaginary, it provides valuable information about the effect _{direction as a response to the applied electric field. For convenience, we} of the presence of a rigid boundary on the electrophoretic behavior of a

assume that the particle is stationary, but the fluid moves in the reverse particle. One of the interesting observations is that if an uncharged particle

direction. The boundary conditions associated with Eqs. [ 7 ] and [ 8 ] are is placed in a negatively charged cavity, the direction of motion of the

assumed to be particle may reverse as the ratio ka ( reciprocal Debye length1particle

radius ) varies. The Poisson – Boltzmann equation was linearized in the

theo-retical development. This is realistic if the electrical potential is low, in £rÅ0 and £uÅ0, rÅa , [ 9 ]

general. Questions arise as to what is the criterion for a low electrical

£rÅ 0U cos u and £uÅU sin u, rÅb , [10 ]

potential and whether this criterion is affected by the charged conditions on the interaction surfaces. These questions are discussed in this note.

where£rand£uare the components of v in the r and u directions,

respec-tively.

THEORY

The z component of the electrostatic force acting on the particle, FEz,

can be calculated by We consider a nonconducting, spherical particle of radius a located

at the center of a spherical cavity of radius b . A uniform electric field

E in the z direction is applied. Suppose that the movement of the particle

FEzÅ

**

S

s(0ÇF ) dS , [11]

is slow so that the system is at a quasi-steady state and the distribution of ions follows the Boltzmann distribution. Then the electrical potential, F, is described by the Poisson – Boltzmann equation ( 3 )

where s denotes the surface charge density and dS the surface element of the particle. The z component of the hydrodynamic drag force, FHz, can be

Ç2_{FÅ 0}r eÅ 0

∑

317

NOTE

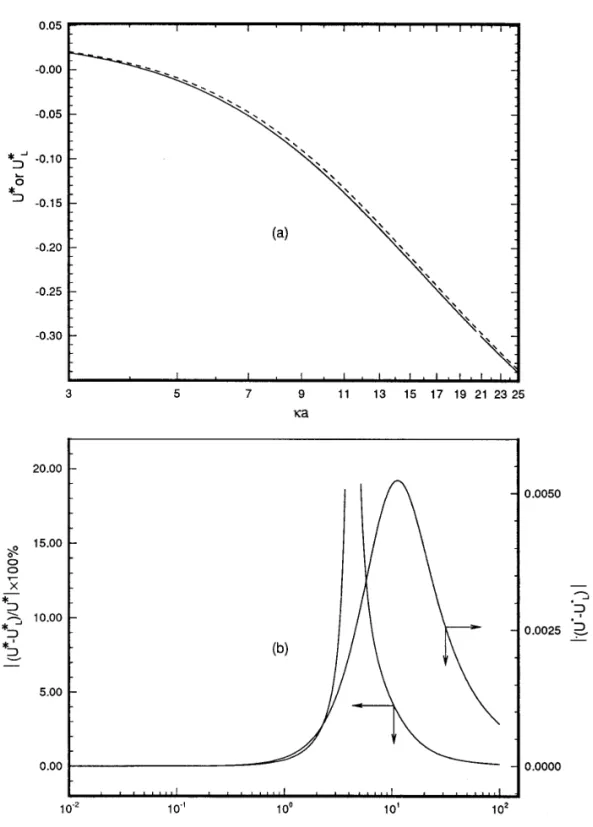
FIG. 1. ( a ) Variation of the scaled mobility as a function of ka . Solid line: present result, U *ÅUh / ejbE ; dashed line: result based on the linearized Poisson – Boltzmann equation, U *LÅULh / ejbE . ( b ) Variations of the relative percentage deviationÉ( U *0U *L) / U *É1100% and the absolute deviation

ÉU *0U *LÉas functions of ka . Key: faÅ0, fb(ÅFbz1e / kT )Å 01, z1being the valence of the cation, and lÅ0.833.

In summary, Eqs. [ 2 ] , [ 3 ] , [ 7 ] , and [ 8 ] need to be solved subject to

FHzÅ2pa 2

F

*

Eqs. [ 5 ] , [ 6 ] , [ 9 ] , and [10 ] . Here, a collocation method based on the pseudospectral method proposed by Canuto et al. ( 5 ) is adopted. Note that Eq. [13 ] is an implicit relation, and, therefore, a trial-and-error procedure /

*

S

D

G

RESULTS

particle can be determined by the condition that the net force exerted on it vanishes at the steady state. We have

Figure 1a shows the variation of the scaled mobility U *ÅUh / eFbE as a function of ka , k being the reciprocal Debye length. For the case

318

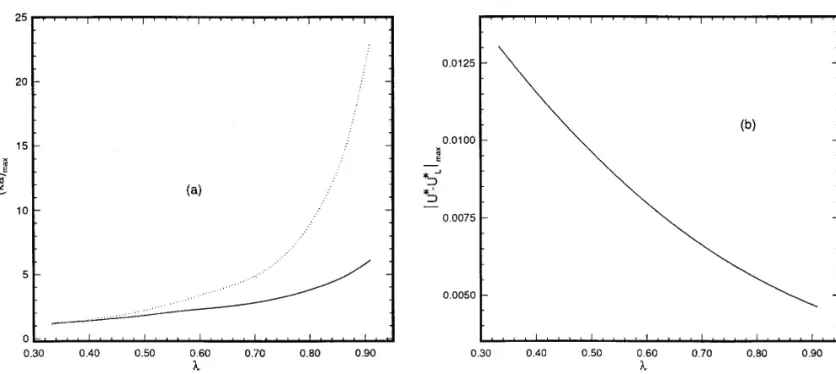
FIG. 2. ( a ) : Variation of ( ka )max as a function of l (Åparticle size / cavity size ) . Solid line: ( ka )max is the value of ka at which É( U * 0

U *L) / U *Édiverges ( or U * vanishes ) ; dotted line: ( ka )maxis the value of ka at whichÉU *0U *LÉis at the maximum. ( b ) Variation ofÉU *0U *LÉ

as a function of l. Key: Same as for Fig. 1 except that l is allowed to vary.

in which the particle is uncharged and the cavity negatively charged, it from this figure,ÉU *LÉwill underestimateÉU *É, in general. The

varia-is defined as tions of the percentage deviation,É( U *0U *L) / U *É1100%, and the

absolute deviation,ÉU *0 U *LÉ, as functions of ka are illustrated in

Fig. 1b. Note that although the former diverges at the point U * vanishes, kÅ( ekT / e2_/

∑

jz

2

j)01. [14 ]

it still provides valuable information. First, it suggests that the differ-ence between U * and U *L is negligible if ka is small (ß2 ) or large

The scaled mobility based on the linearized Poisson – Boltzmann (®20 ) . Second, it reveals that the deviation in the electrophoretic mo-bility can be significant even if U * is appreciable. As an example, the equation, U *LÅULh / eFbE , is also presented in Fig. 1a. As can be seen

319

NOTE

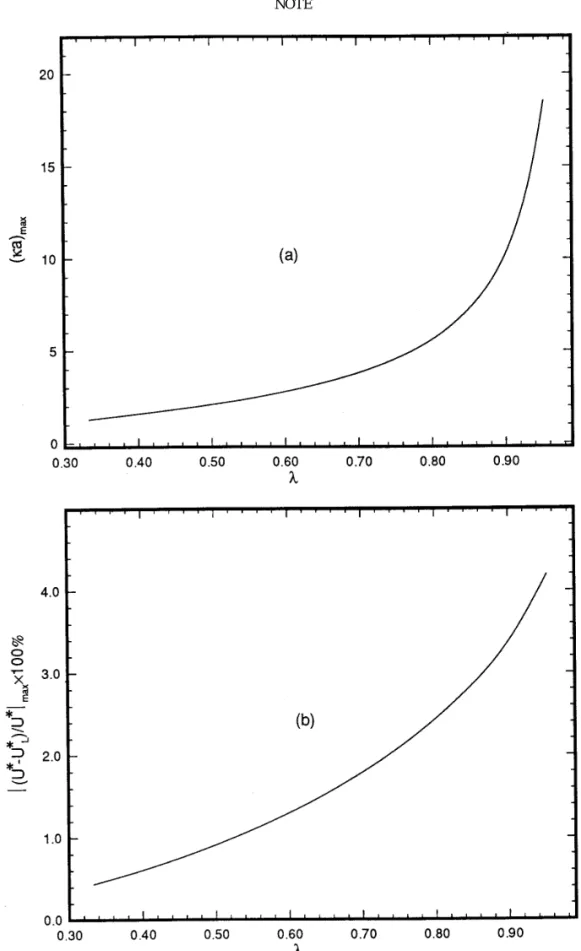
FIG. 4. ( a ) Variation of ka at whichÉ( U *0U *L) / U *Émax1100% occurs, ( ka )max, as a function of l ( particle size / cavity size ) . ( b ) Variation of

É( U *0U *L) / U *Émax1100% as a function of l. Key: faÅ1, fbÅ0.

of l ( particle size / cavity size ) are illustrated in Figs. 2a and 2b, respec-relative deviation of U *L from U * is on the order of 15% at kaÅ3.3

tively. The former shows that ( ka )maxincreases with l, and the latter

( or 5.2 ) , and U * is 0.15 ( or00.15 ) at this ka . Figure 1b also shows

that the absolute deviation, ÉU * 0 U *LÉ, has a maximum, ÉU * 0 reveals thatÉU *0U *LÉmaxdecreases with l. The variation ofÉU *0

U *LÉmax, at a certain ka , ( ka )max. For convenience, ( ka )maxis also de- U *LÉmaxas a function of the absolute scaled surface potential of cavity

ÉfbÉ(ÅÉFbÉz1e / kT , z1being the valence of the cation ) is illustrated in

fined as the value of ka at whichÉ( U *0U *L) / U *Édiverges ( or U *

320

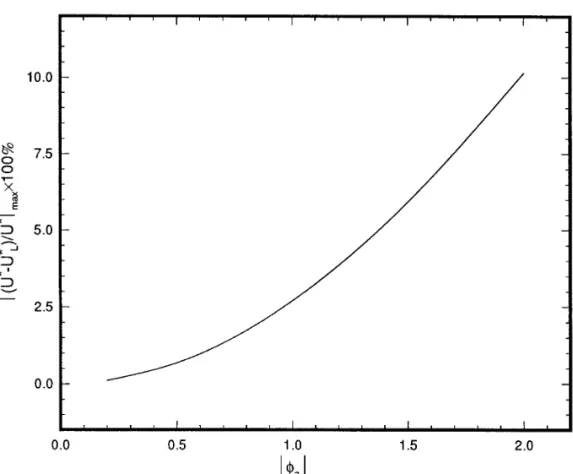
FIG. 5. Variation ofÉ( U *0U *L) / U *Émax1100% as a function of the absolute scaled surface potential of particleÉfaÉ(ÅFaz1e / kT ) , z1being the

valence of the cation, for the case lÅ0.833. Key: faÅ1, fbÅ0.

absolute deviation. It should be pointed out that the deviation of U *L REFERENCES

from U * can be serious even if the electrical potential is low. For example, if l Å 0.833, the relative percentage deviation, É( U * 0

1. Zydney, A. L., J. Colloid Interface Sci. 169, 476 ( 1995 ) .

U *L) / U *É1100%, is on the order of 10%, even ifÉfbÉis lower than

2. Henry, D. C., Proc. R. Soc. A 133, 106 ( 1931 ) . 0.5 ( orÉFbÉ°12.5 mV ) .

3. Hunter, R. J., ‘‘Foundations of Colloid Science.’’ Oxford Univ. Press, For the case in which a particle is positively charged and a cavity

Oxford, 1989. uncharged, U * never vanishes, and, therefore, É( U * 0 U *L) / U *É is

4. Happel, J., and Brenner, H., ‘‘Low Reynolds Number Hydrodynam-finite. Figure 4 summarizes the variations of ( ka )max and É( U * 0

ics.’’ Martinus Nijhoff, The Hague, 1983.

U *L) / U *Émax1 100% as functions of l. Here, ( ka )maxis the value of

5. Canuto, C., Hussaini, M. Y., Quarteroni, A., and Zang, T. A., ka at which É( U * 0 U *L) / U *Émax 1 100% has the maximum. The

‘‘Spectral Methods in Fluid Dynamics.’’ Springer-Verlag, New variation ofÉ( U *0U *L) / U *Émax1100% as a function of the absolute

York, 1986. scaled surface potential of particleÉfaÉ(ÅFaz1e / kT ) is shown in Fig.

5. In general, the percentage deviation in the electrophoretic mobility _{Eric Lee}

is smaller than that if a particle is uncharged and a cavity negatively

Jhih-Wei Chu charged, and the mobility based on the linearized Poisson – Boltzmann

Jyh-Ping Hsu1

equation is satisfactory even if the surface potential of particle is

medium. _{Department of Chemical Engineering}

We conclude that, depending on the charges on particle and cavity sur- _{National Taiwan University} faces, the deviation in the mobility based on the linearized Poisson – Boltz- _{Taipei, Taiwan 10617} mann equation can be serious even if the electrical potential is low. In _{Republic of China} particular, if a particle is uncharged and a cavity negatively charged, use

of the linearized Poisson – Boltzmann equation can be inappropriate.

Received June 6, 1997; accepted October 9, 1997

ACKNOWLEDGMENT

1_{To whom correspondence should be addressed. Fax: 886 – 2 – 3623040.}

This work was supported by the National Science Council of the Republic

E-mail: t8504009@ccms.ntu.edu.tw. of China.