Fault-free Hamiltonian cycles in faulty butterfly graphs

Fault-Free Hamiltonian Cycles in Faulty Butterfly Graphs

Shien-Ching Hwang and Gen-Huey Chen

Department of Computer Science and Information Engineering, National Taiwan University, Taipei, TAIWAN

Email: ghchen@csie.ntu.edu.tw

Abstract

The butterfly graphs were originally defined as the underlying graphs of FFT networks which can perform the fast Fourier transform (FFT) very eficiently. Since butterfly graphs are regular of degree four, it can tolerate at most two edge faults in the worst case in order to establish a Hamiltonian cycle. In this paper, we show that butterfly graphs contain a fault-free Hamiltonian cycle even

if

it has two random edge faults.

1 Introduction

The butterfly graphs were originally defined as the underlying graphs of FFT networks [7] which can perform the fast Fourier transform (FFT) very efficiently. An excellent description of the butterfly graphs can be found in [lo]. The butterfly graphs were known to be an instance of the Cayley graphs (see [2]). The Cayley graphs [I], which represent a category of symmetric and regular graphs derivable from permutation groups, have been shown very suitable to serve as network topologies.

Cycles in networks are usefd to many applications such as indexing, embedding linear arrays and rings [SI,

computing fast Fourier transforms [6], etc. Wong [I21 showed that r-dimensional k-ary butterfly graphs is

Hamiltonian-connected if r is odd, and Hamiltonian- laceable if r is even. Barth and Raspaud [3] constructed two edge-disjoint Hamiltonian cycles in r-dimensional binary butterfly graphs. Then, Bermond et al. [5]

generalized their work by constructing k edge-disjoint Hamiltonian cycles in r-dimensional k-ary butterfly graphs, where k 2 2. Bermond et al. [4] also constructed edge- disjoint Hamltonian cycles in directed r-dimensional k-ary butterfly graphs.

Since faults may happen when a network is put in use, it is practically important to consider faulty networks. In this paper, we construct a Hamiltonian cycle in a faulty r-dimensional binary butterfly graphs.

The rest of this paper is organized as follows. In the next section, some necessary definitions and notations are introduced and some fundamental properties of butterfly

graphs are shown. A Hamiltonian cycle in a faulty butterfly graph is established in Section 3. Finally, this paper concludes with some remarks in Section 4.

2

Preliminaries

For convenience we use BF(r) to denote an r-dimensional binary butterfly graph. There are r levels, numbered 0 , 1,

. .

., r

-

1, associated with BF(r). Each level contains 2‘ vertices that are labeled with 2‘ binary sequences of r symbols. Hence there are r2‘ vertices in BF(r). A vertex of level l labeled with

popl...prl

is denoted by Cl,

poP1...Prl>,

where 0 I

I

I r

-

1 and 0

I

P,

5 1 for all 0 2 j I r - 1 . Each vertex 4,

popl...prl>

is connected to four vertices: <l

-

1 mod r, popl...p/-20p,...prl>, <I - 1 mod r,

POPI.-PI-~IPI-.

PPI>,

<I + 1 mod r,

PoP~-.P~-~OP,+~

...pr-]>,

and <l

+

1 mod r, OpOOp,~~~~,-lOOp,+,...Op~l>. In the rest of this paper, we assume that all arithmetic computations with respect to the symbols and the levels are performed modulo 2 and modulo r, respectively. A formal definition of BF(r) is as follows.

Definition 1. The vertex set of BF(r) is {<l,

popl...prl>

10

I / < r - 1 and 0 6

p,

5 1 for all 0 5 j I r

-

I}. The edge set of BF(r) is

{(a,

popl..,prl>,

</

+

I ,

p o ~ I ’ . . . p r - l ~ )

1

O 5 I I r - 1 and

0,

=

p,’

for all 0 I j 5 r

- 1

and j # I ) . Moreover, (4,

p0pI,..prl>,

4

+

1,

po’pI‘~-~r-l

3 ) is said to be an i-edge if pi’ =

Clearly, BF(r) is regular of degree four and its edges exist between adjacent levels. Level 0 and level r - 1 are considered adjacent. Since BF( 1) has trivial structure and BF(2) is a multigraph, we assume

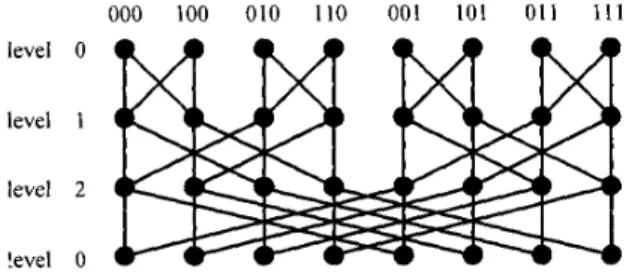
r

1 3 throughout this paper. The structure of BF(3) is illustrated in Figure 1, where level 0 is replicated. BF(r) thus defined was named wrapped butterfly graphs in [IO].

A cycle C in BF(r) is said to be an i-cycle if its edges are all i-edges. Suppose (U, v) is an i-edge of BF(r), where

u is assumed of level / and v is assumed of level l

+

1. Let

+

i, where 0 I i 5 1.

Lo

( U ) = A(u) = v (or u =f;-l(v)),

A’

( U ) =

A(

A’-)

(U)>,

and

A-’

( U ) =

A-’

(

A-’’’

(U)) for j 2 1. Then, (U, &(U), f,’(u),

...,

f:-’ ( U ) , f , ’ ( u ) = U) is a 0-cycle, denoted by

307

C0(u). We say that C0(u) is the 0-cycle induced by U . Each

0-cycle in BF(r) has length r.

000 100 010 110 001 101 011 111 level 0

level 1

level 2

!eve1 0

Figure I . The structure of BF(3) with level 0 replicated. Suppose U = 4,

p0pi.-prl~

and U ’ = <I1,

Po’PI ‘--P,-I

3

are two distinct vertices of BF(r). It is not difficult to see that C0(u) = C,(U’,) if

p0pl-.prl

=

po’pI’.-p,.-i’,

and C0(u) n C0(u’,) is empty else. Hence, there are 2‘ vertex-disjoint (disjoint for short) 0-cycles in BF(r). For each 0-cycle we assign the vertex of level 0 to be the cycle leader. In subsequent discussion, we use C o ( ~ o ~ I ~ ~ ~ ~ p l ) to denote the 0-cycle induced by <O,

po/31...pp-l>.

We say that two disjoint cycles in BF(r) are adjacent if there exists an edge between them.

Lemma 1. In BF(r),

Co(~oPI...pr-l)

is adjacent to r disjoint

0-cycles, i.e.,

Co(/30pI~~~~l-I(~l

+

i)p,+I...p,-i)

for all 1 I i

<

1 a n d O < j I r - 1.

Proof. Suppose

cO(POPI-.P,-O=(E,

&(E),

f,’

( E ) , .

.

.,

f:-’

( E ) ,

for

(e)

= E), where E = <O,

pOpi...ppi>.

There are 2 r vertices of BF(r) that are adjacent to one vertex of

C o ( ~ o ~ l ~ ~ ~ ~ r l ) but not contained in

Co(/30BI-.pr-l).

These 2 r vertices can induce 2 r 0-cycles that are adjacent to Co(p&.-p,.-~). In the following, we show that r of them are disjoint.

SinceA(E) =

4,

(Po

+

1)pl..,p,-,>

andfi(

f,’

( E ) ) = <j +

1 ,

popl-.P,-i(P,

+ 1)P,+I-Pr-I>, COY;(E)) has cycle leader

<O,

(Po

+

I)/31-.p,-i>

and COY;( f,’ ( E ) ) ) has cycle leader <O,

p0pi...P,-,(p’

+

l)fl,+I-.pr-l>, where 1 I j 2 I’

-

1. Similarly, CO(

A-’

( E ) ) and CO(

A-’

( f,’ ( E ) ) ) have cycle leaders CO,

popi..@r-I

-

1)> and <O,

POPI.-PJ-@,-I

-

I)p,...p,,>,

respectively. It is not difficult to see that all different cycle leaders form the set {CO,

/?~p~...fi-~(P,

+

l)p,+I.~.p,-l>

1

0 r j

<

r

-

1 } whose size is r. These different

0 Suppose C and C’ are two adjacent cycles in BF(r), and (U, v’) and (v, U’) are two edges between C and C’. Then (U, v’,) and (v, U’,) are said to be a crossing pair of level 1 between C and C’ if (U, v) and (U‘, v’) are two edges of C

and C’, respectively, between levels

I

and 1

+

1. In subsequent discussion, we define

dflpopI...P,-t,

Po‘PI

‘...

PPI’)

= j if & f P,’and

p,

= p,‘for all 0 5 i 5 r

-

1 and i # j . cycle leaders can induce r disjoint 0-cycles.

A condensation of BF(r), denoted by CBFo(r), is defined as follows. Each 0-cycle

Co(popi~~~prl)

in BF(r.) corresponds to a vertex

p&-..pPI

of CBFo(r), and every pair of adjacent 0-cycles in BF(r) correspond to an edge of CBF,(r). That is, CBFo(r) has vertex set

(pop~.-p,.-l

I ,p,

E ( 0 , 1 ) for all 0 S j I r - I ] ancl edge set

{(popI...pr-.l,

popl...p,-I(P,

+

l)p,+l~~~p,.-l)

1

0 I j S r

-

1 ) according to Lemma 1. We note that CBFo(r:) is isomorphic to the r-dimensional hypercube [l I]. Each path (xi, x2,

...,

x,) in CBFo(r) has d f l ~ , - ~ , x,) f &fix,, x,+~) for all 2 5 i

Lemma 2. Suppose Co(x) and

CO@)

are two adjacent

0-cycles in BF(r). There are exactly two edges between them which form a crossing pair of level drf(x, y).

Proof. Suppose d f l x , y ) = 1, and assume x =

popI...prI

and Y =

Po~I...~,-I~/~I+I...~,-I,

where f

PI’.

There are two edges

(4,

PoPI-.P,-I>,

<I + 1,

POSI...P,-IP~‘~O~+~...P,-I>)

and (‘1

+

1,

popI...prl>,

4,

popI...p

~-Ipl‘p,+i...pr-l>)

between Co(x) and Cob), which form a ‘crossing pair of level 1. There is no other edge between C,(x) and Cob).

Lemma 3. A path (xi, x2, . . ., x,) of length m

-

1 in CBFo(r)

corresponds to a cycle of length mr in BF(r) which contains the vertices of Co(xl), CS3(x2),

...,

Co(x,,), where 2

m

-

1.

m I 2‘.

Proof. According to Lemma 2 , fhere is a unique crossing

pair of level d f l x l , x2) between Co(xl) and Co(x2). We assume that (U,, v2) and (vI, u2) are the crossing pair, where u t and u2 are of level dzfix,, x2) and vi and v2 are of level d i f x , , x2)+l. There is a cycle of length 2 r in BF(r) which contains the crossing pair and all the edges of Co(xl) and

Co(x2) but ( U , , vl) and (u2, v2).

Similarly, there is a unique crossing pair, say (w:, t j ) and (f2, w3), of level dif(x?, x3) between Co(x2) and C,1(x3), where w 2 and w3 are assumed of level dif(x2, x3) and f:! and t3 are assumed of level drj(x2, x3)

+

1. Refer to Figure 2. Since dflx,, x 2 ) f dif(x2, x3), there is a cycle of length 3 r in BF(r) which contains the crossing pair

(wz,

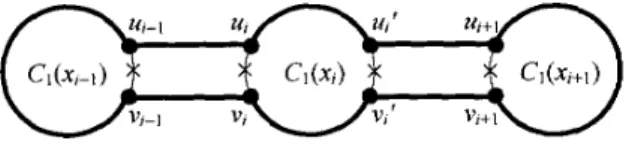
t3) and (t2, wj), the crossing pair ( U ] , vr) and (vl, u2), and all the edges of (w3, f3). The merging can proceed with Co(x4), Co(x5), ..., Co(x,), sequentially, and finally, a cycle of length ,mr in cO(xi), cO(X2), and CO(x3) but ( U 1 3 vi), (U22 v2), (w2, f 2 ) , and

BF(r) can result. 0

Figure 2. Constructing a cycle of length 3r by merging CO(XI), CO(X~), and cO(X3)-

Suppose u =

<I,

popl.-pr-,>

is a vertex of BF(r). Then

( U , J ( u ) ,

A ' ( # ) ,

...,

A " ( u ) )

is a 1-cycle, denoted by C,(U). We say that C , ( U ) is the 1-cycle induced by U . Each

1 -cycle in BF(r) has length 2r.

Suppose u = <I,

/30/31-.pp,>

and U' = <l,

po'pI'-.p,.-13

are two distinct vertices of BF(r). It is not difficulty to see that C,(u) = C,(u') if they have vertices in common. Hence, there are 2'' disjoint 1-cycles in BF(r). Since

A"

( U ) = '1,

(Po

+

t ) ( P , -t t ) - @ p l

+

t)> for integer t 2 I , Cl(u) = C,(u') if and only if

p;

=

p,

+

1 for all 0

Ij

I r

-

1 . The following lemma is clear, and so the proof is omitted.

Lemma 4. Suppose C,(u) and C,(v) are two adjacent

I-cycles in BF(r), and uo E C,(u) is adjacent to vo E C,(v). Then, f;' (uo) E C,(u) is adjacent to

J;'

(vo) E Cl(v).

Lemma 5. Suppose Cl(u) and Cl(v) are two adjacent

I-cycles in BF(r), and uo E C,(u) is adjacent to vo E Cl(v).

There are two adjacent vertices uo' E C,(u) and vo' E C,(v) so that uo' is adjacent to u0 and vo' is adjacent to vo.

Proof. Suppose uo =

<I,

popl.-ppl>

and vo =fo(uo) = <f + 1,

/30pl...pr-l>.

We let uo' = f i ( u o ) =

<f

+

1,

popI...pl-I

(p[

+

I)PI+~-.P,.-I>

E Cdu) and VO' =

A-'

( Y O ) = <I,

PoPI.-PI-I<PI

-

I)/3/t1...pr-,>

E Cl(v). Since uo' =fo(vo'), uo' is adjacent to

vol. 0

Lemma 6. There are 4 edges between every two adjacent

I-cycles in BF(r).

Proof. Suppose C l ( u ) and C,(v) are two adjacent I-cycles

in BF(r), and uo E C,(u) is adjacent to vo E C,(v). According to Lemma 5, there are two adjacent vertices uo'

E C,(u) and vo' E Cl(v) so that uor is adjacent to uo and vo' is adjacent to vo. According to Lemma 4,

J;'

(uo) E Cl(u) is adjacent to

L'(v,)E

C,(v)

and J;' (uo3 E C , ( u ) is

adjacent to f;'(v0') E C,(v). Hence, there are 4 edges

For each I-cycle we assign the vertex of level 0 whose leftmost symbol is 0 to be the cycle leader. For example, the I-cycle (<O, 001>, 4, 101>, <2, I l l > , <O, 110>, <I,

010>, <2, OOO>, <O, 001>) in BF(3) has cycle leader <O, 001>. In subsequent discussion, we use Cl(Oj3,p2.-p,,) to denote the 1-cycle induced by CO,

Op&..p,.-~>.

Lemma 7. In BF(r),

Cl(Oplpz~~~p,,)

is adjacent to r

disjoint I-cycles, i.e., C,(O(/?,

+

l)(pz

+

l)... (PPI + 1)) and

CI(Op1p2...p,

-,(p,

+

l)pJ+l...pr-I)

for all 1 r j 5 r

-

1.

Proof. Suppose U =

<Z,

pOpl-.ppI>

E Cl(OpI/32.-/3r-I).

There are two vertices of BF(r) that are adjacent to U but

not contained in

CI(OpIp2...prl)

.

These two vertices can induce two I-cycles which are all adjacent to

between Cl (u) and C,(v).

U

C,(Oplp2~~.~,.-,).

We use S to denote the set of these two

1 -cycles. Similarly, there are two vertices of BF(r) that are adjacent to J;' ( U ) =

<I,

(Po

+

])(PI

+

I)..@,.-,

+

I)> but not contained in C,(Op,p,

...p,.-,).

We use T to denote the set of the two 1 -cycles that are induced by the two vertices. Recall that C,(u) = C,(u') if and only if

pJ'

=

p,

+

1 for all 0 5 j 5 r - 1 , where U ' = '1,

po'pl

'...fir-,

3 is a vertex of BF(r) and U ' # U . We have S = T. Hence, it suffices to consider only r consecutive vertices of

Cl(OpI~~~~.pp~),

say E,

A(&),

f,' ( E ) , .

.

.,

Lr-'

(E), where E = <O,

Op,p2...p,,>.

There are 2r vertices of BF(r) that are adjacent to one of E,

A(&),

J;' ( E ) ,

...,

( E ) but not contained in Cl(OP,Pz.-Ppt>. They are

f o ( ~ ) ,

f;'

(E), f o V ; ( ~ ) ) ,

fi'

V;(E))>

fo(

A'

(E)), I f; (

A'

( E ) ) , ' . . 7

fo(

Ar-I

( E ) ) ,

f;'

(

Ar-'

(E)). Since c ~ o ( E ) ) = <o,

0(pI

+

I)(/$

+

I)...

@pi + I)> and

A-""cfo(fi'

( E ) ) ) = <O,

OPtPz-@,

-

1)

D,+I...~,-I>,

C,uo(~)) has cycle leader <O,

0(pI

+

I)(p2

+

1 )

+ I)> and C,Y-,( f; ' ( E ) ) ) has cycle leader "0,

Op,p2

..@, -

I)fi+,...p,.+>,

where 1 2j

<

r - 1.

Similarly, C,

(f;'(~))

has cycle leader <O, 0pIp2,..pr-,

+

I)>, C,(

fi'V;(E)))

has cycle leader <O,

O(p,

- 1)

(p2

-

I)..@rl

-

I)>, and C,(

f;'

(A'

( E ) ) ) has cycle leader <O, 0p,/32...P,-2

(PI-,

+ I)p,~..ppl>,

where 2 S j S r - 1 . All

the cycle leaders constitute the following set.

w

= {<O, O@,

+

1)(/?2

+

I)-@-,

+

I)>} U

The lemma follows because

IWl=

r.

{<O,

opIp2"'pJ-I(p/+

I)@)tI"'p?,>

1

'-

I}.

0 A condensation of BF(r), denoted by CBF,(r), is defined as follows. Each I-cycle

CI(OpIp2-.ppl)

in BF(r) corresponds to a vertex

pIP2...prl

of CBF,(r), and every pair of adjacent I -cycles in BF(r) correspond to an edge of CBFl(r). That is, CBFl(k, r) has vertex set

{pIp2...prl

10 I

@,<

1 for all 1

<

i 2 r

-

1 } and edge set {(pI/?2..-p,..l, 1))

I

1 I i 5 r

-

1) according to Lemma 7. We note that the ( r

-

1)-dimensional hypercube is a spanning subgraph of CBFl (r )

.

Lemma 8. A path of length n

-

1 in CBFl(r) corresponds

to a cycle of length 2nr in BF(r).

Proof. Suppose (x,, x2,

...,

x,) is a path of length n - 1 in

CBFI(~). According to Lemma 5, there exist two adjacent vertices U , - , , v,-, of

CI(x,-,)

and two adjacent vertices U , , v, of C,(x,) so that u , - ~ and v,-, are adjacent to U , and v,,

respectively, where 2 2 i

I

n - 1 . Similarly, there exist two adjacent vertices U,', v,' of C,(x,) and two adjacent vertices

pf-dpf

+ 1 ,pf+I.-pr-I>, ( P I P 2 4 - ' ,

(PI

+ 1 )@z + 1

1.-

(PPI

+

U , + ] , v , + ~ of

Cl(x,+l)

so that U,’ and v,’ are adjacent to u,+~ and

v,+~, respectively. It is assured by Lemma 6 that U,’

and v,‘ E! { U , , v,} can be determined. A cycle of length 2nr

U

{ U , , v,} in BF(r) can be constructed as shown in Figure 3.

Figure 3 . Constructing a cycle of length nkr in BF(r).

CBF0(r) that contains e. Since CBF0(3) is isomorphic to the three-dimensional hypercube, our claim is true for CBFO(3). We then assume that our claim is true for CBFo(r

-

I),

where r - 1 2 3.

Suppose e = ( v l , v2) is an edge of CBFo(r), where v1 E

Hc: and v2 E H i . There exist vl’ E He0 and v2‘ E

ff:

so that vl’ is adjacent to vl, vz’is adjacent to v2, and v I ’ is adjacent to v2‘. By our assumption, there are a Hamiltonian cycle in H,“ that contains the edge (vl, vl’) and a Hamiltonian cycle in H i that contains the edge (v2, v;!’). Since e and (vl’, v2’) are two edges between the two Hamiltonian cycles, there is a Hamiltonian cycle in CBFo(r) that contains e, (vl’, v2’), and all the edges of the two Hamiltonian cycles but (vl, vl’j ancl (v2, v2’).

Suppose q = d f l e l ) and (xl, x2,

..., x2.-,

, xI) is a ~ ~ ~cycle iin H; l . Then, ~ ( ~x1(4)

,

x ~ ) ~ ,

.

i.

.,

x$j, ~ , ~

x,(~) ) is a Hamiltonian cycle in

HJI

. If drf(e2) = d g t ? ] ) , A Hamiltonian cycle of CBFl(r) can be obtained using

Grad code. a cyclically ordered sequence of 2“ distinct binary codewords forms a d-dimensional Grad code, denoted by G(d), provided every two adjacent codewords differ in exactly one dimension

[SI,

where d 2 1. G(d) can be constructed recursively as follows. Initially, let G( 1)=(0,

1). For i 2 2, G(j)=(OG(i - I), ]GR(i - I)), where GR(j - I )

then (xI,

xl(,,)

,

xp)

,

x2, xj, x?) , x y ) , ...,

xi?!,-],

xi??, ,

xz,., , xl) is a Hamiltonian cycle in CBFo(r) that contains el denotes the reverse of G(i

- 1).

For example, G(2) =

(OG(l), lGR(l))=(OO, 01, 11, IO) and G(3) = (OG(2),

1 GR(2)) = (000, 001, 01 1,010, 110, 11 1, 101, 100). Since G(r

- 1)

contains all the vertices of the ( r - 1 )-dimensional hypercube and every two adjacent codewords of G(r - 1 ) correspond to an edge of the ( r - 1)-dimensional hypercube, G(r - 1 ) corresponds to a Hamiltonian cycle in the ( r

-

I)-dimensional hypercube. Thus, G ( r - 1 ) corresponds to a Hamiltonian cycle in CBFl(r).

3 Hamiltonian cycles in faulty

BF(r)

Since BF(r) is regular of degree four, it can tolerate at most two edge faults in the worst case in order to establish a Hamiltonian cycle. In this section, we show that BF(r)

and e2. If dfle,) # d f l e , ) , we assume e2 E He: without loss of generality. There is a Hamiltonian cycle, say ( y ~ , y 2 , .

..,

y *,., , yl), in He: that contains e 2 . Suppose el = (yY, yj”) for some 1 I s I 2” and e2 = (yr, ;v,+]) for some 1 I t 5

A Hamiltonian cycle in CBFo(r) that contains e l and e2 can be established as (yS+l, yS+2,

. .

., y2r.l ,

YI,

yz, .

.

.,

y,, yp)

,

y.r-l ( q ) , .

.

., yf” , y:? , y$j-, , .

.

.:, y f . ys+l) if s f t, and

( Y , 2 Ys, YS+I,

.’.,

Y2’4 t Y l , YZ,

...

) Ys-1, Y,-1 7 Ys-29 ...?

~ 4 4 ) , yi2 , yi!j-l ,

. .

.,

y::;, ys4’ ) i f s = t.

CI

( 4 ) ( 4 ) (4)

contains a Hamiltonian cycle even if it has two edge faults. We observe that CBFo(r), which is isomorphic to the r-dimensional hypercube, is recursive. Suppose e =

(popI...

PPI, po’p~’.-p~-~’)

is an edge of CBFo(r), where

dflpop1...

Lemma 10. Suppose el and e2 are two distinct edges of

CBFo(r). There exists a Hamiltonian path in CBFo(r) that does not contain el and e2.

PPI,

po’pI’...prl’)

= q is assumed. The two subsets of Proof. Suppose q = d f l e l ) and (xl, x2,

...,

x,,.,

,

xI) is a vertices with

p,,

= 0 and

p,,

= I , respectively, form a

partition of the vertex set of CBFo(r). The two subgraphs of CBFo(r) that are induced by the two subsets are isomorphic to CBFo(r - I). In subsequent discussion, we let difle) =

dflpopl...prI,-I,

po’pI’...p,-I’)

and use Heo and Hl to. denote the two subgraphs, respectively. The following three lemmas state findamental properties of CBFo(r).

Lemma 9. Suppose e l and e2 are two distinct edges of

CBFo(r). There exists a Hamiltonian cycle in CBFo(r) that contains el and e2.

Proof. We first show by induction on r that given an

arbitrary edge e of CBFo(r), there is a Hamiltonian cycle in

Hamiltonian cycle in H.3

.

If dif(e2) = drf(el), determine an edge (xA, x j q ) )

e

{ e l , .ez} for some 1

I

s 5 2?’. A Hamiltonian path in CBFo(r) that does not contain el and e2 can be established as ( x:?; , x:\

, ...,

x i 4 ) ,

~$1

,

,

x,, x,+I,

...,

x2.+ , X I , x2,

...,

x d . Ifd,Xed

x ( 4 )

f & ( e l ) , we assume e2 E H: without loss of generality. There is a Hamiltonian cycle, say (yl, y2,

...,

Y ~ , . ~ , yl), in H6: that contains e2. Suppose e2 = (y,, yr+]) for some 1 S t

i 2‘-’. A Hamiltonian path in CBFo(r) that does not contain

x ( 4 )

Lemma 11. Suppose el and e2 are two distinct edges of

CBFo(r). There exists a Hamiltonian path in CBFo(r) that contains el but does not contain e2.

Proof. Suppose q = d f l e l ) and (xl, x2,

...,

xz,., , xl) is a

Hamiltonian cycle in He:

.

Then el = ( x ~ , xsy) ) for some 1

I s I 2r-’. If dfle,) = d f l e ] ) , a Hamiltonian path in CBFo(r) that contains e l but does not contain e2 can be established

as (x,.+~, xsi2,

...,

x,,.,

, xI, x2,

..

., x,, ):x

,

, ..., x ( ~ ) 1 ,

x ( Y ) z,., ,

,.,-,

,

. .

., x!!;

1.

~ f d f l e , ) # d f i e , ) , we assume e2 E He: without loss of generality. There is a Hamiltonian cycle, say @,, y2,

...,

y2,., , yl), in He: that contains e2. Suppose e2 = (yr, J I / + ~ ) for some 1 I t I 2p1. A Hamiltonian

path in CBFo(r) that contains el but does not contain e2 can be established as

bl,

yl-l, ..., y,, yjy’, y::;,

...,

y?., ( Y ) ,

Y y ) , x y , ‘.., Y~~~>Y.s-l,Y.,-2> . ‘ . , Y I > Yz,-i 3 Y2‘-‘-I f ‘..3Yl+l)

Y$j ,

(Y) ( Y )

i f s 5 t, and

Oi/+l,

y/+2,

..

’ > y.5, Y ,

x$j-, ,

..

., y,,, , y,+l, A+?, . .., y 2 , + , yl, y,, ..., ifs 2 t +

1 . When s = 1 , the subpath

(~$1

, y ? ) , xp), ..., ys“)

7 .Y-[

,

... > ( Y )

shrinks to a vertex y$! and the subpath @3-I, ys-2,

. .

., yl,

y2,., ) shrinks to a vertex y

*,.,

.

When s = 2“, the subpath ( y ; “ ) , y;?j , ,

.

..,

yj:{) shrinks to a vertex y,(y) and the subpath Cys+I, yS+,,

.

. ., y2,-, , y l ) shrinks to a vertex yI

.U

The following theorem is the main result of this paper.

Theorem 1. BF(r) with two edge faults contains a

Hamiltonian cycle.

Proof. Suppose ( U ] , v l ) and ( U , , v2) are two edge faults in BF(r), where { U ] , v l } f {u2, v 2 } . We observe that each edge of BF(r) is either a 0-edge or a 1-edge and each 1 -edge (0-edge) connects two distinct 0-cycles (1 -cycles). There are three cases discussed below.

Case 1. ( u I , v I ) and ( U * , v2) are 0-edges. If ( U ] , v l ) and (u2, v2) belong to the same 0-cycle, say Co(x), then there are

two distinct 0-cycles, say Cob) and CO@), that are adjacent to Co(x), and there are two 0-edges, say (uI

’,

v1 ’) E Cob) and (u2’, v2’) E Co(z), so that (uI, vl’) and (vl, ul’) are a crossing pair between Co(x) and Cob) and (u2, v2’) and (v2,

u2’) are a crossing pair between Co(x) and Co(z). Since (x, y ) and (x, z ) are edges of CBFo(r), Lemma 9 assures a Hamiltonian path in CBFo(r) that contains (x, y ) and (x, z). According to Lemma 3, the Hamiltonian path corresponds to a Hamiltonian cycle in BF(r). The Hamiltonian cycle does not contain ( U ] , VI), (ul’, vl?, ( U , , v2), and (u2’, v2’)

(refer to the proof of Lemma 3).

We then consider that (ut, v l ) and (u2, v2) belong to two

distinct 0-cycles, say Co(x) and CO@), respectively. If either ( u I , v2) and (vl, u2) or ( u l , u2) and (vl, v2) are a crossing pair between Co(x) and Cob), then a Hamiltonian cycle in BF(r) that does not contain ( u I , v l ) and (u2, v2) can be obtained, similarly, by the aid of Lemma 9 and Lemma 3.

If neither ( u I , v2) and (vl, u2) nor ( u I , U , ) and ( v l , v2) are a

crossing pair between Co(x) and CO@), then there are two 0-cycles, say Co(x’) and CO@’), that are adjacent to Co(x) and Cob), respectively, and there are two 0-edges, say (uI’,

v I ’) E Co(x’) and (u2’, v2’) E CO@’), so that ( u I , vI ’) and (vI,

u I ’) are a crossing pair between Co(x) and Co(x’) and ( U , , v,’) and ( v 2 , u2’) are a crossing pair between Co(x) and CO@’). A

Hamiltonian cycle in BF(r) that does not contain ( U ] , vI),

(uI’, VI’), ( u ~ , v2), and (u2‘, v2’) can be obtained, similarly, by the aid of Lemma 9 and Lemma 3.

Case 2. (ul, v I ) and (u2, v2) are I-edges. If ( u I , v l ) and (u2. v 2 ) connect the same pair of 0-cycles, say Co(x) and CO@), then they are a crossing pair between Co(x) and Coo/)

according to Lemma 2. Since (x, y ) is an edge of CBFo(r), Lemma 10 assures a Hamiltonian path in CBFo(r) that does not contain (x, y ) . Similarly, the Hamiltonian path corresponds to a Hamiltonian cycle in BF(r) that does not contain ( u l , v I ) and (u2, v2). Otherwise, suppose (ul, v l ) connects Co(x) and Cob) and ( U * , v2) connects Co(z) and

Co(w). A Hamiltonian cycle in BF(r) that does not contain (ul, v l ) and (u2, v2) can be obtained, similarly, by the aid of Lemma 10 and Lemma 3.

Case 3. One of ( U ] , v l ) and ( U ? , v2) is a 0-edge and the other

is a I-edge. Without loss of generality, we assume that ( u I , v l ) is a 0-edge and (u2, v,) is a I-edge. We hrther assume that ( U ] , v l ) belongs to Co(x) and (u2, v2) connects Co(z) and

Co(w). There is a 0-cycle, say Cob), that is adjacent to Co(x), and there is a 0-edge, say (uI

‘,

vI ’) E Co b) , so that ( u I , v1 ’) and ( v I , u l ’) are a crossing pair between Co(x) and

Cob). If { z i l r v l } n { u 2 , v 2 } is empty, then (x, y ) and (z, w) are two distinct edges of CBFo(r). According to Lemma 1 1 , there is a Hamiltonian path in CBFo(r) that contains (x, y ) but does not contain ( z , w ) . Similarly, the Hamiltonian path corresponds to a Hamiltonian cycle in BF(r) that does not contain ( U ] , vI) and ( U , , v2).

If { U ] , v I } n {u2, v 2 } is not empty, we assume vI = u2 E

Co(w) without loss of generality. Hence Co(x) = Co(w). According to Lemma 2 , there is a I-edge, say (u2’, v2’), so

that ( U * , v2) and (u2’, v2’) are a crossing pair between Co(x)

and Co(z), where u2, u2’ E Co(x) and v2, v2’ E C&). If u I #

u2‘, then ( x , y ) and (x, z ) are two distinct edges of CBF0(2r). A Hamiltonian cycle in BF(r) that does not contain ( U ’ , vI)

and (u2, v2) can be obtained, similarly, by the aid of Lemma

1 1 and Lemma 3.

If u1 = uz’, then CO@) = Co(z) is implied. Recall that G(r

- 1) corresponds to a Hamiltonian cycle in CBF,(r). We use C = (xl, x2,

..., x2,.,

,

xI) to denote the Hamiltonian cycle, where x I , x2,

...,

x2,., form a G(r - I ) , Suppose

C,(Ox,)

is the 1-cycle in BF(r) that contains (u2, vz), where

1 I s I 2?’. According to Lemma 8, C - { x ~ } , which is a path of length 2?’

-

2 in CBF,(r), corresponds to a cycle of length r2‘

-

2r in BF(r). We use

d

to denote the cycle. The vertex set of

d

and the vertex set of Cl(Ox,) constitute a partition of the vertex set of BF(r). We show in the following that a Hamiltonian cycle in BF(r) that does not contain ( u l , vl) and (uz, v2) can be obtained by carehlly adding the vertices of

C,(Ox,)

to

d

.

Without loss of generality, we assume v2 = f i ( u z ) and let Cl(OX3) = ( U Z , f i ( U Z ) (= vz), f ; ’ ( U Z ) ,

. .

.,

f r - ’

(a

hZr

( U ? ; )

(= u2)). For 1 I t I r, let w ,

=fo(

f i Z r - l (u2)) E C and IV,‘ =

fil

(

A*‘

( U * ) ) E . It is not dificult to see that

(f;”’-’

(uz), w,) and

(Az‘

(uz), w,’) are a crossing pair between Cl(Ox,) and

d .

Since {wZ1?1, wzP} n {wzq-l, wzq} is empty for all p # q, a Hamiltonian cycle in BF(r) can result if (

fi2‘-’

(uz), w,), (

f;”

(4,

w,?, and (

h2‘-’

x2‘

(uZ)) are added to

d

and (w,, w,’) is removed from

d

for all 1 5 t I r. Since (uz, v2) = (

fiZr

(uz), f i ( t i 2 ) ) P

{(A2‘-’

(uz), J2‘ (u2))

1

1 I t I r } , the Hamiltonian cycle does not contain (uz, v2). Moreover, the Hamiltonian cycle does not contain ( u l , v l ) because (vl, MI) P {( f;”-l(u2), w,), (

A2‘

(uz), w,’)

I

1 I t I r } , as explained below.

We havefo(vl) = uI because vz = f i ( u 2 ) and (uz, v2) (= (vI, U ’ ’ ) ) and (uz’, v2’) (= (uI, vl’)) are a crossing pair

between CO@) and Co(z) (= CO@)). Since f;‘ (u2) = f;‘ (VI) +fo(vl) = uI for all 1

<

c

< 2r

and

f;‘

( U ? ) =

vI

only when

c

= 2r, we have (vl, u I ) P

{(Azr-’

(uz), w0,

( A z r

(uz), w,’)

I

1

I t I r } if u I # w,’. The latter is true because w,‘ =

0

fJ-I (

A2‘

(u2)) = fJ-I (U21 = &I (VI) *fo(Vl> = U I .

4

Conclusion and discussion

faults contains a Hamiltonian cycle. Since CBFo(r) is In this paper, we showed that BF(r) with two edge

isomorphic to the r-dimensional hypercube, Lemma 9,

Lemma IO, and Lemma 11 are also valid for the latter. We suspect that Theorem 1 can be generalized as follows: An

r-dimensional k-ary butterfly graph with 2k - 2 edge faults contains a Hamiltonian cycle. However, the proof seems very hard.

References

S. B. Akers and B. Krishnamurthy, “A g r o u p theoretic model for symmetric interconnection networks,” IEEE Transactions on Computers, vol. 39, no. 4, pp. 555-566, 1989.

F. Annexstein, M. Baumslag, and A. L. Rosenberg, “Group action graphs and parallel architecture$;,” SIAM Journal on Computing, vol. 19, no. 3, pp. D. Barth and A. Raspaud, “Two edge-disjoint Hamiltonian cycles in the butterfly graph,” Information Processing Letters, vol. 5 I , pip. J.-C. Bermond, E. Darrot, 0. Delmas, and S. Perennes, “Hamilton circuits in the directed wrapped butterfly netwoirk,” Discrete Applied Mathematics, vol. 84, pp. 21-42, 1998.

J.-C. Bermond, E. Darrot, 0. Delmas, and S. Perennes, “Hamilton cycle: decomposition of the butterfly network,” Parallel Processing Letters, vol. 8, no. 3, pp. 371-385, 1998.

P. Fragopoulou and S. G. Akl, “A parallel algorithm for computing Fourier transform on the star graph,” Proceedings of the International Conference on Parallel Processing, 199 1, lpp. 100- 106.

J. Y. Jou and J. A. Abraham, “Fault-tolerant FFT networks,” IEEE Transactions on Compuers, vol. 37, no. 5, pp. 548-561, 19813.

S. Lakshmivarahan and S. K. Dhall, Analysis and Design of Parallel Algorithms: Arithmetic and Matrix Problems, McGrarn-Hill, New York, hlY, 1990.

S. Lakshmivarahan, J. S. Jwo, and S. K. Dhall, “Embedding of cycles and grids in star graphs,” Journal of Circuits, Systems, and Computers, vol. 1, no. 1, pp. 43-74, 1991.

F. T. Leighton, Introduction to Parallel Algorithms and Architecture: Arrays. Trees.Hypercubes, Morgan Kaufman, San Mateo, CA, 1992.

Y . Saad and M. H. Schultz, “Topological properties of hypercubes,” IEEE Tra.nsactions on Computers, vol. 37, no. 7, pp. 867-872, 1988.

S. A. Wong, “Hamilton cycles and paths in butterfly graphs,” Networks, vol. 26, pp. 145-150, 1995. 544-569, 1990.