Computational Study of Reaction Pathways for the Formation of Indium Nitride from
Trimethylindium with HN
3: Comparison of the Reaction with NH
3and That on TiO
2Rutile (110) Surface
†Yi-Ren Tzeng,*,‡P. Raghunath,*,‡ Szu-Chen Chen,‡and M. C. Lin‡,§
Center for Interdisciplinary Molecular Science, Institute of Molecular Science, National Chiao Tung UniVersity, Hsinchu 300, Taiwan, and Department of Chemistry, Emory UniVersity, Atlanta, Georgia 30322
ReceiVed: December 29, 2006; In Final Form: February 10, 2007
The reactions of trimethylindium (TMIn) with HN3and NH3are relevant to the chemical vapor deposition of indium nitride thin film. The mechanisms and energetics of these reactions in the gas phase have been investigated by density functional theory and ab initio calculations using the CCSD(T)/Lanl2dz//B3LYP/ Lanl2dz and CCSD(T)/Lanl2dz//MP2/Lanl2dz methods. The results of both methods are in good agreement for the optimized geometries and relative energies. These results suggest that the reaction with HN3forms a new stable product, dimethylindiumnitride, CH3-IndN-CH3via another stable In(CH3)2N3(dimethylindium azide, DMInA) intermediate. DMInA may undergo unimolecular decomposition to form CH3InNCH3by two main possible pathways: (1) a stepwise decomposition process through N2 elimination followed by CH3 migration from In to the remaining N atom and (2) a concerted process involving the concurrent CH3migration and N2elimination directly giving N2+ CH3InNCH3. The reaction of TMIn with NH3forms a most stable product DMInNH2following the initial association and CH4-elimination reaction. The required energy barrier for the elimination of the second CH4molecule from DMInNH2is 74.2 kcal/mol. Using these reactions, we predict the heats of formation at 0 K for all the products and finally for InN which is 123 ( 1 kcal/mol predicted by the two methods. The gas-phase reaction of HN3with TMIn is compared with that occurring on rutile TiO2(110). The most noticeable difference is the high endothermicity of the gas-phase reaction for InN production (53 kcal/mol) and the contrasting large exothermicity (195 kcal/mol) released by the low-barrier Langmuir-Hinshelwood type processes following the adsorption of TMIn and HN3on the surface producing a horizontally adsorbed InN(a), Ti-NIn-O(a), and other products, CH4(g) + N2(g) + 2CH3O(a) [J. Phys. Chem. B 2006, 110, 2263].
Introduction
Indium nitride is an important III-nitride semiconductor with a stable wurtzite crystal structure; it has been used for visible optoelectronics, high-efficiency solar cell, and other potential applications.1-4 This chemically stable and robust InN has a useful range of band gaps, 0.7-2.1 eV, which result from the crystallinity and quantum confinement effects.5-9 Deposition of InN films of varying thickness on TiO2nanoparticle films has been demonstrated by low-pressure organometallic chemical vapor deposition (OMCVD) near 700 K with continuous UV irradiation using hydrazoic acid (HN3) and trimethylindium (TMIn), which are perhaps the most efficient precursors.6,9,10 The resulting InN films on TiO2 exhibit a broad UV/visible absorption between 390 and 800 nm quite similar to that of Graetzel’s “black” dye,11indicating a promising possibility for photovoltaic applications.10c
The main aim of this work is to study the various reaction pathways of acid (HN3) and base (NH3) with trimethylindium that may be involved in the chemical vapor deposition of InN using the density functional theory (DFT) and ab initio calculations. Recent work on indium metal complexes has shown that the widely used B3LYP and MP2 methods with Lanl2dz
basis sets are quite suitable for geometry and property predic-tions.12Especially, we hope to examine the mechanistic differ-ence between the interaction of TMIn with acid and base in terms of initial reactant complexation and to ensure fragmenta-tion of the associafragmenta-tion complexes. These studies explore the stability and structural properties of the various possible species, which we believe could help in predictions of the formation of InN in the gas phase and on semiconductor surfaces. The calculated geometries and heats of formation could be helpful for the likely identification of the species in the laboratory. Computational Methods
The equilibrium geometries of the reactants, transition states, intermediates, and products for the HN3and NH3with TMIn reactions are optimized by DFT at the B3LYP level and ab initio at the MP2 level using the Gaussian 03 program.13The B3LYP method consists of Becke’s three-parameter hybrid exchange function combined with the Lee-Yang-Parr correlation func-tion.14Due to the limitation of available basis set for the indium atom, our calculations are limited to the approximation of effective core potentials, among which we selected the Los Alamos effective core potential plus double-ζ (lanl2dz) as the
basis set.16 All the geometries are analyzed by harmonic vibrational frequencies obtained at the same level and character-ized as minima (no imaginary frequency) or as a transition state (one imaginary frequency). Transition-state geometries are then used as an input for intrinsic reaction coordinate (IRC)
calcula-†Part of the special issue “M. C. Lin Festschrift”.
* Corresponding authors. E-mail: yiren.tzeng@gmail.com (Y.-R.T); raghuputikam@yahoo.com (P.R.).
‡National Chiao Tung University. §Emory University.
6781
J. Phys. Chem. A 2007, 111, 6781-6788
10.1021/jp0690345 CCC: $37.00 © 2007 American Chemical Society Published on Web 03/28/2007
tions to confirm the transition state is connected to the designated reactants and products.16The higher-order correlation energy corrections of both B3LYP and MP2 energies were obtained at a single point using the CCSD(T)/LANL2DZ method.17We find the two popular optimization methods give rise to very similar geometries and relative energies, which are also very close to the single point calculation results by CCSD(T) with the geometries predicted with both methods. Zero-point vibrational energy (ZPVE) corrections based on the unscaled frequencies are applied to all of the calculated energies.
As alluded to above, one of the major purposes of this study is to compare the difference between the HN3+ TMIn reaction pathways in the gas phase and those on the TiO2rutile (110) surfaces.18Reference 18 used the Vienna ab initio simulation package (VASP) for geometrical optimization with a plane wave basis set. The exchange-correlation function was treated with the local-density approximation (LDA). The generalized gradient approximation (GGA) used for the total energy calculations was that of the Perdew-Wang 1991 (PW91) formulation, which has been shown to work well for surfaces.
Results and Discussion
TMIn + HN3Reaction. As aforementioned, the geometries of all the gas-phase reactants, intermediates, products, and
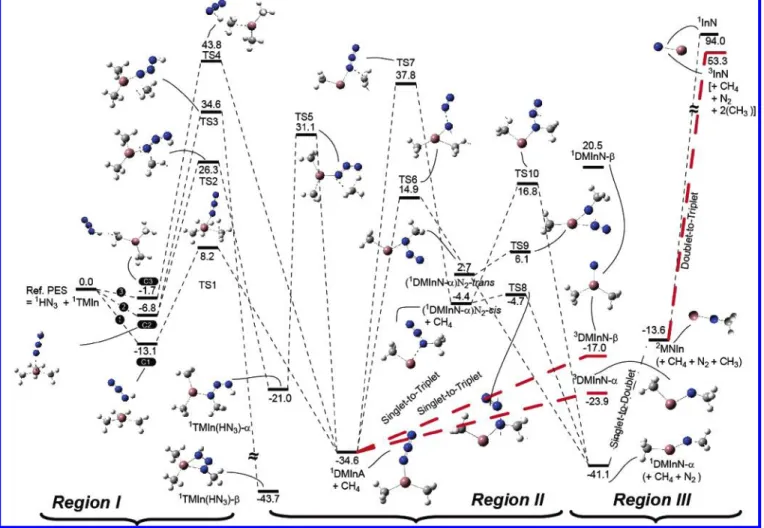
transition states have been optimized at the B3LYP/Lanl2dz and MP2/Lanl2dz levels of theory; the results are similar. Therefore we show only the B3LYP results given in Figure 1. The predicted energies with both basis sets, summarized in Table 1, are also very close, particularly after additional single-point calculations with the CCSD(T)/Lanl2dz level. The potential energy diagram obtained at the CCSD(T)/Lanl2dz//B3LYP/ Lanl2dz level of theory is presented in Figure 2. The relative energies are calculated with respect to the reactants In(CH3)3 + HN3. Because there exist several molecular intermediates, whose triplet-state energies are closer to or lower than those of the corresponding singlet states, to distinguish them, we con-nect the adiabatic (singlet-to-singlet) reaction pathways with (regular) dashed lines and the nonadiabatic (singlet-to-triplet) surface crossing ones with long and thick dashed lines. The following discussions will be based on the results of the calculations at the CCSD(T)/Lanl2dz//B3LYP/Lanl2dz level of theory.
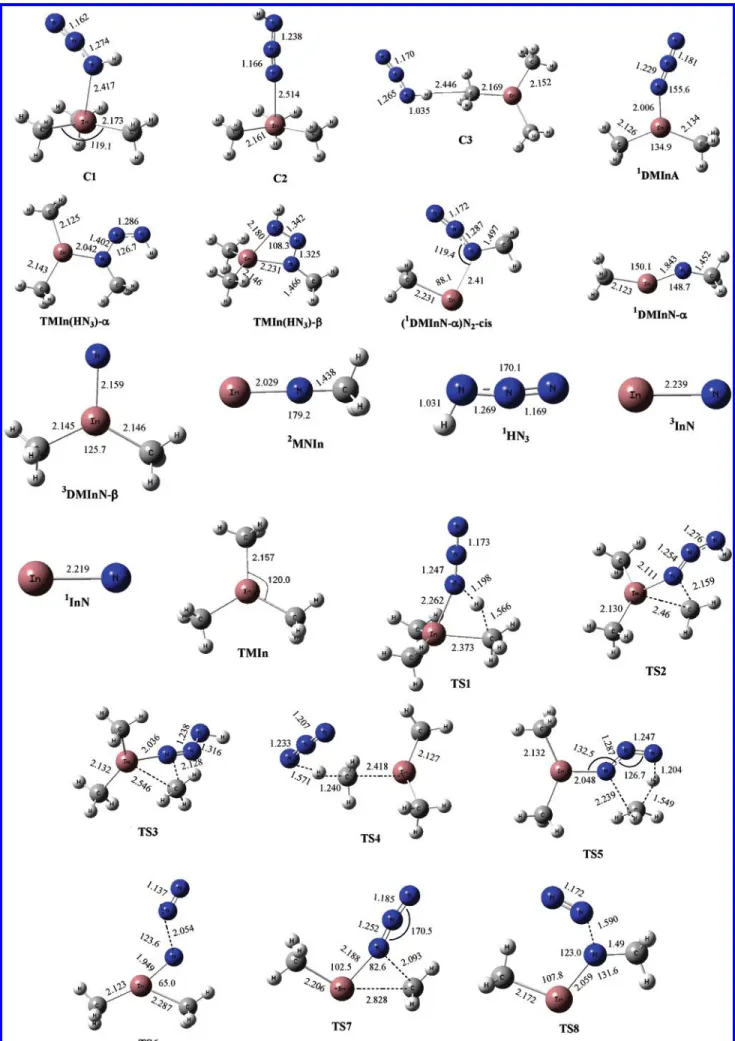
To facilitate the discussion that follows, we will designate the HN3atoms in the N(1)N(2)N(3)H(4) order. Trimethylindium is a planar molecule, and the bond length of In-C is 2.157 Å with low-energy rotational barriers for the methyl groups. In a short range, as shown in region I in Figure 2, we found HN3 reacting with TMIn can form three molecular complexes, which Figure 1. Part 2 of 2. All optimized geometries of the intermediates and the transition states calculated using the B3LYP/Lanl2dz level. Bond
lengths are in angstroms and angles in degrees.
TABLE 1: Relative Energies (kcal/mol) of Various Species in the TMIn + HN3Reaction Calculated at the Different Levels
species
B3LYP/Lanl2dz
+ ZPVE MP2/Lanl2dz+ ZPVE CCSD(T) Lanl2dz//B3LYP/Lanl2dz+ ZPVE CCSD(T) Lanl2dz//MP2/Lanl2dz+ ZPVE
1HN 3+1TMIn 0.0 0.0 0.0 0.0 NNN(H)-In(CH3)3, C1 -9.8 -12.5 -13.1 -13.3 HNNN-In(CH3)3, C2 -5.1 -7.2 -6.8 -6.9 NNN(H)-(CH3)In(CH3)2, C3 -1.7 -2.1 -1.7 -1.8 TS1 2.6 2.2 8.2 8.7 TS2 23.0 39.3 26.3 25.4 TS3 31.0 49.6 34.6 33.1 TS4 35.8 32.1 43.8 42.3 1TMIn(HN 3)-R -21.5 -10.1 -21.0 -21.4 1TMIn(HN 3)-β -45.7 -32.3 -43.7 -43.9 TS5 28.7 34.1 31.1 28.8 1DMInA + [CH 4] -35.7 -45.2 -34.6 -33.7 TS6 + [CH4] 32.4 26.2 14.9 15.9 TS7 + [CH4] 39.7 41.8 37.8 39.3 1DMInN-R-N 2(cis) + [CH4] -0.5 -1.3 -4.4 -4.6 1DMInN-R-N 2(trans) + [CH4] 7.6 5.3 2.7 6.2 TS8 + [CH4] 4.9 1.5 -4.7 -3.1 TS9 + [CH4] 8.7 14.5 6.1 2.6 TS10 + [CH4] 18.8 16.8 1DMInN-R + [CH 4+ N2] -21.0 -43.4 -41.1 -40.2 3DMInN-R + [CH 4+ N2] -8.8 -18.6 -23.9 -22.2 3DMInN-β + [CH 4+ N2] 4.0 -13.2 -17.0 -16.2 1DMInN-β + [CH 4+ N2] 41.3 30.1 20.5 21.1 2MNIn + [CH 4+ N2+ CH3] 9.3 -5.5 -13.6 -12.4 3InN + [CH 4+ N2+ 2(CH3)] 88.6 63.9 53.3 54.7 1InN + [CH 4+ N2+ 2(CH3)] 131.7 110.4 94.0 95.3
are denoted as NNN(H)-In(CH3)3(C1), HNNN-In(CH3)3(C2), and NNN(H)-(CH3)In(CH3)2(C3). In the initial steps, the most reactive N(3) atom bonding with H in HN3can directly associate with the indium atom in In(CH3)3by a barrierless process that forms with NNN(H)-In(CH3)3 and exothermic complexation processes. The exothermicities are around 13.1 kcal/mol at the CCSD(T)/Lanl2dz//B3LYP/Lanl2dz level. As shown in Figure 1, nitrogen points toward the In atom in the top and middle of the molecule at a distance of 2.417 Å (2.441 Å by MP2). The complex has C1symmetry, and the C-In-C angle has changed from 120 to 119.1°. The second possible initial reaction, N(1) of HN3addition toward the In atom of TMIn, to form a complex, C2, has a 6.8 kcal/mol binding energy. Here the bond length of In-N is 2.514 Å. The formation of complex C3 corresponds to the head on approach of H(4) of HN3toward one of the CH3 groups of TMIn and has 1.7 kcal/mol binding energy calcu-lated at the CCSD(T)//B3LYP method. The geometry of the In(CH3)3fragment in the complex shows very little change in one of the In-C bond length 2.169 Å (compared to an isolated In(CH3)3).
In the next reaction step, the two molecular complexes C1 and C3 lie below the reactants by 13.1 and 1.7 kcal/mol and the H(4) atom of the HN3 can react with one of the methyl groups intramolecularly to eliminate CH4, producing DMInA (dimethylindium azide), (CH3)2InN3, via TS1 and TS4, respec-tively. This CH4elimination process is predicted to have a low potential barrier (TS1) of 21.3 kcal/mol with a large exother-micity that lies -21.5 kcal/mol below that of the reactant C1. The transition vector is dominated by the motion of hydrogen,
which is 1.198 Å from the nitrogen and 1.566 Å from the carbon. The large exothermicity mainly shows in part from the formation of the strong C-H bond in part from the weak C-In bond. Relatively, the CH4elimination process in C3 needs to go over a much higher potential barrier via the TS4 transition state, the C3 first stretches the N(3)-H and In-CH3 bonds, and then using the N(3) as a pivotal point, the whole N3, leading by the N(1), swings toward the In atom with the In-N bond length of 4.350 Å. As N(1) approaches the In atom, the CH4 detaches from the In to form DMInA. This process has a potential barrier of 45.5 kcal/mol and an exothermicity of -32.9 kcal/mol.
On the basis of the schematic potential energy surface (PES) presented in Figure 2, comparing with C1 and C3 the C2 exhibits a much more complex decomposition and isomerization process. Because the N3in HN3is approximately linear and sits nearly perpendicularly on the plane of TMIn in C2, the distance between the H(4) and any CH3group is too long (>5.70 Å) to allow for a direct CH4elimination. As a result of this geometry limitation, the C2 preferably undergoes isomerization processes, leading to the formation of two stable molecules. One of the processes, going through TS2 with a barrier of 33.1 kcal/mol, involves the migration of one CH3 group toward N(1). This brings the CH3group closer to the H(4), allowing the linear N3 in HN3to bend in the direction bringing the CH3group even closer to the H(4). This rearrangement leads to the formation of a stable planar Cssymmetry TMIn(HN3)-R molecule, whose H(4)-CH3distance now becomes 2.359 Å and whose energy lies -14.2 kcal/mol below the C2 complex.
Figure 2. Potential energy surface of the HN3+ TMIn reaction. Relative energies (kcal/mol) calculated using the CCSD(T)/Lanl2dz//B3LYP/
The migration of the CH3group in C2, as mentioned above, can go through a slightly higher barrier 41.4 kcal/mol TS3 transition state. This causes the N3 to bend in the opposite direction, which increases the distance between the H(4) atom and the attacked CH3group, and brings the N(3) toward the In atom. This process leads to the formation of a stable ringlike TMIn(HN3)-β molecule. This molecule has a Cssymmetry with
planar structure formed by the H, three N, and the attacked C and In atoms, and the distance between the H(4) and three C atoms in each CH3group is roughly the same (4.363, 4.363, and 4.323 Å). Because of the large H(4)-CH3group distance in the TMIn(HN3)-β, we did not carry out further search for any possible CH4 elimination pathway. The energy level of TMIn(HN3)-β lies -36.9 kcal/mol below the C2 complex.
Further decomposition of TMIn(HN3)-R produces the DMInA and CH4through a CH4elimination process, by which the H(4) migrates toward the CH3group connected to the N(1) atom. The H(4) appears to bond strongly to the N(3) atom, as we observe that the migration of the H(4) is accompanied by a bending of the N(1)-N(2)-N(3) angle of 126.7°. Also because this process needs to break a strong N-CH3 bond, the CH4 elimination process goes through the TS5 transition state with a barrier of 52.1 kcal/mol, even though the exothermicity is -13.6 kcal/mol.
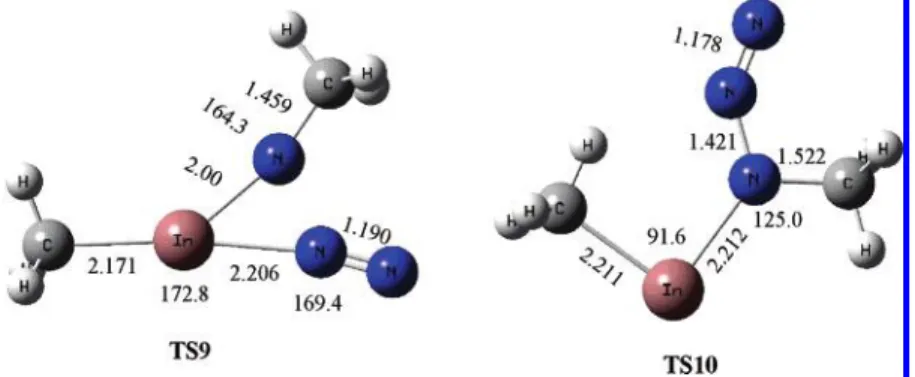
As seen from the PES in region II in Figure 2, the decom-position of DMInA produces the most stable CH3InNCH3 denoted as DMInN-R and N2 molecule. This process may proceed via two branched pathways, both of which are going through high potential barriers. This concerted process involving the concurrent CH3migration and N2elimination requires the 49.5 kcal/mol energy barrier at TS6. Another channel is a two-step process. The first two-step, going through the TS7 transition state with a potential barrier of 72.4 kcal/mol, is an isomerization process, involving the migration of one CH3from the In atom to the closest N atom to form the (DMInN-R)N2-cis structure. The second step is a unimolecular decomposition process, which can either go through TS8 (NNNIn-cis) with a barrier of 0.3 kcal/mol or TS10 (NNNIn-trans) with a barrier of 21.2 kcal/ mol predicted by the CCSD(T)//B3LYP method. Thus, starting from DMInA, its isomerization by methyl migration to (DM-InN-R)N2-cis is endothermic by 30.2 kcal/mol. The following fast fragmentation of the latter isomer via TS8 is exothermic by 36.7 kcal/mol. It is interesting to note that the (DMInN-R)-N2-cis may also undergo a cis-to-trans isomerization process, with the trans lying 7.1 kcal/mol higher than the cis. The trans isomer has a low-energy barrier (3.4 kcal/mol) for N2elimination via TS9. We also calculated the energy of the optimized singlet DMInN-β, which is an isomer of the singlet DMInN-R. Perhaps
because of the ring strain and the open shell N electronic structure, the singlet DMInN-β lies + 61.6 kcal/mol above the
singlet DMInN-R.
Up to now, we have assumed that the reaction proceeds adiabatically and thus restricted our calculations to the singlet electronic state. Notwithstanding, because the optimized singlet DMInN-β geometry is rather unstable and much higher in
energy than the singlet DMInN-R, the bonding order of the N(3) atom therein gives rise to open-shell electronic structure. We suggest that the N2elimination process could give rise to a triplet N(3) forming the triplet DMInN-β shown in Figure 1 and singlet
N2. As seen from the PES in region III in Figure 2, the calculations predict the triplet DMInN-β to be stable and its
energy is 37.5 kcal/mol lower than the singlet DMInN-β.
Comparatively, the energy level of the triplet DMInN-R is 17.2 kcal/mol higher than the singlet (DMInN-R).
A stepwise unimolecular decomposition of the DMInN-R produces doublet radicals of MNIn and CH3. In this process, breaking of CH3from indium requires 30.3 kcal/mol predicted at B3LYP/Lanl2dz and 27.5 kcal/mol energy at the CCSD(T)// B3LYP level. Similarly, the endothermicity for the reaction of MNIn f InN + CH3, which breaks the CH3from the N atom, is 66.9 kcal/mol and triplet InN lies 40.7 kcal/mol below the singlet InN.
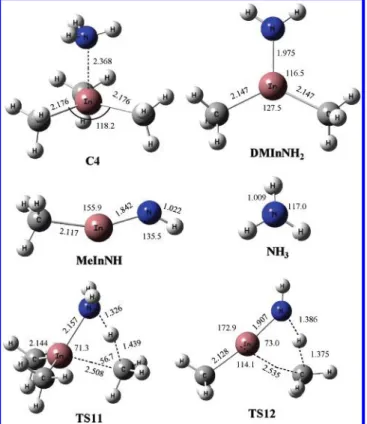
Comparison with the TMIn + NH3 Reaction. It is interesting to compare the TMIn + HN3 reaction with the TMIn + NH3reaction. The calculated structures of intermedi-ates, transition stintermedi-ates, and products of all investigated steps are given in Figure 3, and relative energies are given in Table 2. Figure 3. All optimized geometries of the intermediates and the
transition states calculated using the B3LYP/Lanl2dz level. Bond lengths are in angstroms and angles in degrees.
TABLE 2: Relative Energies (kcal/mol) of Various Species in the TMIn + NH3Reaction Calculated at the Different Levels
species
B3LYP/Lanl2dz
+ ZPVE MP2/Lanl2dz+ ZPVE CCSD(T) Lanl2dz//B3LYP/Lanl2dz+ ZPVE CCSD(T) Lanl2dz//MP2/Lanl2dz+ ZPVE
NH3+ TMIn 0.0 0.0 0.0 0.0 (CH3)3In-NH3, C4 -17.4 -19.6 -20.0 -19.8 TS11 9.2 12.8 14.3 14.2 DMInNH2+ CH4 -22.2 -22.5 -22.6 -22.5 TS12 + CH4 47.5 50.1 51.6 51.4 MeInNH + 2CH4 25.5 19.6 19.7 19.9 2InNH + CH 3+ 2CH4 64.1 62.2 52.7 53.6 3InN + H + CH 3+ 2CH4 160.7 146.0 136.0 136.8 1InN + H + CH 3+ 2CH4 203.9 192.5 176.8 177.4
The potential energy diagram obtained at the CCSD(T)/ Lanl2dz//B3LYP/Lanl2dz level of theory is presented in Figure 4. The association reaction of the electron deficient TMIn and NH3 can form the C4 molecular complex with a calculated binding energy of 20.0 kcal/mol,which is more stable than C1, the most stable (CH3)3In-N(H)N2complex. This 20 kcal/mol binding energy of C4 may be compared with previous calcula-tions of binding energy of 18.2 kcal/mol for (CH3)3In-NH3 using the B3LYP/Lanl2dz* level.12e The structure of the (CH3)3In-NH3 complex has been previously discussed in detail, and the calculated In-N bond length of 2.368 Å agrees well with previous calculations.12e The decomposition of the (CH3)3In-NH3molecular complex to the most stable intermedi-ate DMInNH2,(CH3)2InNH2, and a CH4molecule requires the transition-state energy at TS11 of 34.3 or 14.3 kcal/mol above the reactants predicted at the CCSD(T)//B3LYP level of theory. In this PES, the formation of products DMInNH2+ CH4is most exothermic with 22.6 kcal/mol exothermicity. This amount of energy release is somewhat smaller than that of the analogous CH4-elimination reaction of C1, producing DMInA, 34.6 kcal/ mol. DMInNH2can further undergo a CH4-elimination process, by which the H migrates toward the CH3group connected to the In atom to form MInNH at 19.7 kcal/mol above the reactants. The CH4-elimination process goes through the TS12 transition state with a high-energy barrier of 74.2 kcal/mol. There is no analogous step in the TMIn-HN3system, but the fragmentation of DMInA to produce CH3InNCH3 (DMInN-R) + N2 has to overcome only about a 50 kcal/mol barrier. We could not locate a saddle point for the generation of InN and CH4from MInNH. The energy required for MInNH to decompose into InNH + CH3is 33.0 kcal/mol. It further dissociates without barrier to produce3InN + H with an overall endothermicity of 83.3 kcal/
mol from2InNH. Singlet InN is 40.8 kcal/mol above the triplet InN + H.
Heats of Formation. The predicted heats of formation of InN presented in Table 3 were based on the energies computed at the CCSD(T)/Lanl2dz//B3LYP/Lanl2dz level using TMIn reacting with HN3 and NH3. Based on predicted heats of reactions (∆rH0°) and experimental heats of formation (∆fH0°) of reactants at 0 K, the heats of formation of all intermediate products from both reactions are calculated. Experimentally, the heats of formation are available for the following: (CH3)3In, 49.9 kcal/mol at 298 K (or 53.0 kcal/mol at 0 K); HN3, 71.8 kcal/mol; NH3, -9.3 kcal/mol; and CH4, -16.0 ( 0.08 kcal/ Figure 4. Potential energy surface of the NH3+ TMIn reaction. Relative energies (kcal/mol) are calculated using the CCSD(T)/Lanl2dz//B3LYP/
Lanl2dz method.
TABLE 3: Heats of Reaction (∆rH0°, kcal/mol) and Heats of Formation (∆fH0°, kcal/mol) of Species at 0 K Predicted at the CCSD(T)/Lanl2dz//B3LYP/Lanl2dz Level of Theory
species reactiona ∆
rH0° ∆fH0°
TMIn + HN3
C1 HN3+ (CH3)3In f C1 -13.1 111.7
DMInA C1 f DMInA + CH4 -21.5 106.2
DMInN DMInA f DMInN + N2 -6.5 99.7
MNIn DMInN f MNIn + CH3 27.5 91.3
InN MNIn f InN + CH3 66.8 122.3
TMIn + NH3
C4 NH3+ (CH3)3In f C4 -20.0 23.7
DMInNH2 C1 f DMInNH2+ CH4 -2.6 37.1
MInNH DMInNH2f MInNH + CH4 42.3 95.4
InNH MInNH f InNH + CH3 32.9 92.5
InN InNH f InN + H 83.3 124.2
aThe experimental values are obtained on the basis of the following heats of formation at 0 K: (CH3)3In, 52.97 kcal/mol (calculated from
the 298 K value given in ref 19 using vibrational frequencies in this work); HN3, 71.8 kcal/mol;22NH3, -9.30 kcal/mol;20CH4, -16.0 (
0.08 kcal/mol;20CH
mol.19-22 The predicted ∆
fH0° (0 K) for the five products, C1 [NNN(H)-In(CH3)3], DMInA [(CH3)2InN3], DMInN [(CH3)2InN], MNIn [CH3InN], and InN, are 111.7, 106.2, 99.7, 91.3, and 122.3 kcal/mol, respectively, and have been estimated, as shown in Table 3. In addition,∆fH0°(0 K) for these products (CH3)3InNH3, (CH3)2InNH2, CH3InNH, InNH, and InN are 23.7, 37.1, 95.4, 92.5, and 124.2 kcal/mol, respectively, which are calculated using the TMIn + NH3reaction. The corresponding experimental values are not available. The InN heat of formation determined using the reactions of HN3and NH3with TMIn is approximately same energy, 122.3 and 124.2 kcal/mol, respec-tively, at 0 K. Earlier we employed the same method to evaluate the heats of formation of InO and InS; the predicted values were found to be in good agreement with experimental data.23
Comparison with Reactions on TiO2Rutile (110). Recently, our group has studied the reactions of HN3and TMIn on the TiO2rutile (110) surface by first-principles calculations based on the DFT and pseudopotential method.18Here, we compare the reaction mechanism of the lowest energy pathways of the gas-phase and TiO2surface reactions and how the TiO2rutile (110) surfaces affect the HN3+ TMIn reactions. For comparison purposes, we have rearranged the reference potential18ain Figure 5 to the energy of the most stable adsorbates, which corresponds to the HN3(g) + TMIn(g) + TiO2rutile (110) [see Figure 2 in ref 18a].
Both the reaction pathways in the gas phase and on the TiO2 surface are very similar. On the clean rutile (110) surface, TMIn and HN3can molecularly coadsorb on the surface, giving (H3C)3In-Ob(a) and Ti-NNN(H)-Ob(a) with a total of 62
kcal/mol adsorption energy, where Ob denotes a bridged O atom.18aThe reaction proceeds initially with the approach of the N(3) atom of HN3toward the In atom to form a most stable Ti-NNN(H)-Ob-(H3C)3In-Ob(a) molecular complex. The exothermicity of the above the association complex is 68 kcal/mol. A similar CH4-elimination process yielding CH4(g) and Ti-NNN-(Ob)-In(CH3)2-Ob(a) takes place with a 38 kcal/mol barrier which lies 30 kcal/mol below the reactants, HN3(g) + TMIn(g) + TiO2 rutile (110); the reaction is exothermic by 42 kcal/mol (or 110 kcal/mol exothermic from the reactants). The overall reaction exothermicity producing Ti-InN-O(a) + CH4(g) + 2CH3O(a) + N2(g) was predicted to be 195 kcal/mol, where Ti-InN-O(a) is an InN molecule adsorbed horizontally on the TiO2surface.18aThe gas-surface reaction of TMIn + HN3is therefore very exothermic and can occur easily on TiO2 surfaces, as has been demonstrated experimentally by Wang and Lin.10,18
Conclusions
In this work, we have presented the reaction mechanisms for the reactions of TMIn with HN3and NH3, investigated by DFT (B3LYP) and ab initio (MP2) methods. We predicted that the lowest energy pathway for the HN3 and NH3 + TMIn reactions proceeds by first forming molecular complexes NNN(H)-In(CH3)3(C1) and (CH3)3In-NH3(C4) followed by a CH4-elimination process which goes over a potential barrier of 21.3 and 34.3 kcal/mol to form the DMInN3and DMInNH2, respectively. Then DMInN3 undergoes a concerted process Figure 5. PES of the surface reaction pathways of HN3with TMIn on the TiO2rutile (110) surfaces. (Redrawn with permission from Figure 2 in
ref 18a. Copyright 2006 American Chemical Society.)
involving the concurrent CH3 migration and N2 elimination which requires 49.5 kcal/mol energy barrier to form DMInN (CH3InNCH3). Subsequently, by two series of stepwise CH3 decomposition, DMInN breaks into InN and two CH3radicals. The energy of the triplet InN is 40.7 kcal/mol lower than the singlet. In the case of NH3reaction the elimination of two CH4 molecules to form MInNH requires a high-energy barrier of 74.2 kcal/mol. The MInNH thus formed can decompose into InNH and CH3and finally into InN and H radicals. The total energy required for this process is 83.3 kcal/mol. From these two reactions we calculated the heat of formation of InN at 0 K to be 122.3 and 124.2 kcal/mol. Contrary to the gas-phase processes which produce InN endothermically as alluded to above, the reaction of TMIn with HN3on the rutile TiO2(110) surface via the Langmuir-Hinshelwood mechanism was found to be very exothermic with the final production of an InN molecule horizontally adsorbed on the rutile surface.18a
Acknowledgment. The authors thank the Institute of Nuclear Energy Research (INER), Taiwan, for the funding of this project. M.C.L. acknowledges the support from the Taiwan Semicon-ductor Manufacturing Co. for TSMC Distinguished Professor-ship and for the National Science Council of Taiwan for the Distinguished Visiting Professorship at National Chiao Tung University in Hsichu, Taiwan.
References and Notes
(1) Juza, R.; Hahn, H. Z. Anorg. Allg. Chem. 1938, 239, 282. (2) Jain, M.; Willander, M.; Narayan, J.; Overstraten, R. V. J. Appl. Phys. 2000, 87, 965.
(3) Strite, S.; Morkoc, H. J. Vac. Sci. Technol., B. 1992, 10, 1237. (4) Bhuiyan, A. G.; Hashimoto, A.; Yamamoto, A. J. Appl. Phys. 2003, 94, 2779.
(5) Xu, K.; Yoshikawa, A. Appl. Phys. Lett. 2003, 83, 251. (6) Wakahara, A.; Tsuchiya, T.; Yoshida, A. J. Cryst. Growth 1990, 99, 385.
(7) Matsuoka, T.; Okamoto, H.; Nakao, M.; Harima, H.; Kurimoto, E. Appl. Phys. Lett. 2002, 81, 1246.
(8) Yodo, T.; Yona, H.; Ando, H.; Nosei, D.; Harada, Y. Appl. Phys. Lett. 2002, 80, 968.
(9) Hwang, J.-S.; Wu, C. T.; Chen, K.-H, Chuan, C. M.; Chen, L.-C.; Chen, T. T.; Chen, Y. F.; Lin, M. C. Unpublished work.
(10) (a) Bu, Y.; Ma, L.; Lin, M. C. J. Vac. Sci. Technol., A 1993, 11, 2931. (b) Bu, Y.; Ma, L.; Lin, M. C. Mater. Res. Soc. Symp. Proc. 1993, 335, 21. (c) Wang, J. H.; Lin, M. C. ChemPhysChem. 2004, 5, 1615.
(11) Nazeeruddin, M.-K.; Kay, A.; Rodicio, I.; Humpry-Baker, R.; Muller, E.; Liska, P.; Vlachopoulos, N.; Graetzel, M. J. Am. Chem. Soc.
1993, 115, 6328.
(12) (a) Cardelino, B. H.; Moore, C. E.; Cardelino, C. A.; Frazier, C. A.; Bachmann, K. J. J. Phys. Chem. A 2001, 105, 849. (b) Rothschopf, G. K.; Perkins, J. S.; Li, S.; Yang, D.-S. Phys. Chem. A 2000, 104, 8178. (c) Himmel, H.-J.; Downs, A. J.; Greene, T. M. J. Am. Chem. Soc. 2000, 122, 9793. (d) Tachikawa, H.; Kawabata, H. J. Mater. Chem. 2003, 13, 1293. (e) Nakamura, K.; Makino, O.; Tachibana, A.; Matsumoto, K. J. Organomet. Chem. 2000, 611, 514.
(13) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J. A., Jr.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A. Gaussian 03, Revision C.02; Gaussian: Wallingford, CT, 2004.
(14) (a) Becke, A. D. Phys. ReV. A 1998, 38, 3098. (b) Lee, C.; Yang, W.; Parr, R. G. Phys. ReV. B 1988, 37, 785. (c) Becke, A. D. J. Chem. Phys. 1993, 98, 5648.
(15) (a) Dunning, T. H., Jr.; Hay, P. J. In Modern Theoretical Chemistry; Schaefer, H. F., III, Ed.; Plenum Press: New York, 1977. (b) Hay, P. J.; Wadt, W. R. J. Chem. Phys. 1985, 82, 270. (c) Wadt, W. R.; Hay, P. J. J. Chem. Phys. 1985, 82, 284. (d) Hay, P. J.; Wadt, W. R. J. Chem. Phys.
1985, 82, 299.
(16) (a) Gonzalez, C.; Schlegel, H. B. J. Chem. Phys. 1989, 90, 2154. (b) Gonzalez, C.; Schlegel, H. B. J. Phys. Chem. 1990, 94, 5523.
(17) (a) Cizek, J. AdV. Chem. Phys. 1969, 14, 35. (b) Purvis, g. D.; Bartlett, R. J. J. Chem. Phys. 1982, 76, 1910. (c) Scuseria, G. E.; Janssen, C. L.; Schaefer, H. F., III. J. Chem. Phys. 1988, 89, 7382. (d) Scuseria, G. E.; Schaefer, H. F., III. J. Chem. Phys. 1989, 90, 3700.
(18) (a) Wang, J. H.; Lin, M. C. J. Phys. Chem. B 2006, 110, 2263. (b) Wang, J. H.; Lin, M. C. J. Phys. Chem. B 2005, 109, 20858. (c) Wang, J. H.; Lin, M. C.; Sun, Y. C. J. Phys. Chem. B 2005, 109, 5133.
(19) NIST Chemistry WebBook; NIST Standard Reference Database No. 69; National Institute of Standards and Technology: Gaithersburg, MD, 2005; http://webbook.nist.gov/chemistry/.
(20) Chase, M. W., Jr.; Davies, C. A.; Downey, J. R., Jr.; Frurip, D. J.; McDonald, R. A.; Syverud, A. N. JANAF Thermochemical Tables. J. Phys. Chem. Ref. Data 1985, 14, Suppl. 1.
(21) Ruscic, B.; Litorja, M.; Asher, R. L. J. Phys. Chem. A 1999, 103, 8625.
(22) Gurvich, L. V.; Veyts, I. V.; Alcock, C. B. Thermodynamic Properties of IndiVidual Substances, 4th ed.; Hemisphere: New York, 1989.
(23) Raghunath, P.; Lin, M. C. J. Phys. Chem., submitted for publication (revision).