Secret sharing schemes for graph-based prohibited structures

(1)

P e r g a m o n

Secret Sharing Schemes for

G r a p h - B a s e d Prohibited Structures

H U N G - M I N S U N *

D e p a r t m e n t of Information Management Chaoyang I n s t i t u t e of Technology 168, Gifeng E. Rd., Wufeng, Taichung County

Taiwan 413, R.O.C. hmsun@dscs2, csie. nctu. edu. tw

S H I U H - P Y N G S H I E H

D e p a r t m e n t of Computer Science and Information Engineering National Chiao Tung University

Hsinchu, Taiwan 30050, R.O.C. ssp@csie, nctu. edu. t w

(Received October 1996; accepted June 1997)

A b s t r a c t - - A secret sharing scheme for the prohibited structure is a method of sharing a master key among a finite set of participants in such a way that only certain prespecified subsets of participants cannot recover the master key. A secret sharing scheme is called perfect, if any subset of participants who cannot recover the master key obtains no information regarding the master key. In this paper, we propose an efficient construction of perfect secret sharing schemes for graph-based prohibited structures where a vertex denotes a participant and an edge does a pair of participants who cannot recover the master key. The information rate of our scheme is 2/n, where n is the number of participants. (~) 1998 Elsevier Science Ltd. All rights reserved.

K e y w o r d s - - C r y p t o g r a p h y , Data security, Information theory, Secret sharing scheme.

1 . I N T R O D U C T I O N

I n 1987, I t o et al. [1] d e s c r i b e d a g e n e r a l m e t h o d of s e c r e t s h a r i n g c a l l e d Secret Sharing Scheme (SSS) w h i c h allows a m a s t e r key t o b e s h a r e d a m o n g a finite set o f p a r t i c i p a n t s in s u c h a w a y t h a t o n l y c e r t a i n p r e s p e c i f i e d s u b s e t s of p a r t i c i p a n t s c a n recover t h e m a s t e r key. L e t P b e t h e set of p a r t i c i p a n t s . T h e set o f all s u b s e t s of P , d e n o t e d b y 2 P, is c a l l e d t h e p o w e r set o f P . W e use t h e n o t a t i o n X \ Y = {x I x E X a n d x ~ Y } t o d e n o t e t h e difference o f t w o sets X a n d Y. T h e c o l l e c t i o n of s u b s e t s of p a r t i c i p a n t s t h a t c a n r e c o n s t r u c t t h e m a s t e r k e y in t h i s w a y is c a l l e d access structure ( d e n o t e d b y F ) . T h e c o l l e c t i o n o f s u b s e t s o f p a r t i c i p a n t s t h a t c a n n o t r e c o n s t r u c t t h e m a s t e r k e y is c a l l e d prohibited structure ( d e n o t e d b y A ) [2]. T h e n a t u r a l r e s t r i c t i o n is t h a t r is m o n o t o n e i n c r e a s i n g a n d A is m o n o t o n e d e c r e a s i n g , t h a t is, if A E F a n d A C_ B C P , if A E A a n d B C_ A C_ P , then B ~ F, then B E A. a n d

*Author to w h o m all correspondence should be sent.

This work was supported in part by the National Science Council, Taiwan, under contract NSC-87-2213-E-324-003. Typeset by .A.A~-TEX 131

(2)

132 H.-M. SUN AND S.-P. SmEH

If A = 2 P \ F , then we say the structure (F, A) is complete [2]. In the special case where F = {A I A C P and IA] _> m} and A = {A ] A C P and ]A] _< m - 1}, the secret sharing scheme is called an (m, n)-threshold scheme [3,4], where IPI = n. Let K be the master key space and S be the share space. The information rate of the secret sharing scheme is defined to be the ratio between the master key size and the maximum size of the shares [5]. Here we use the notation p = log 2 ]Kl/log 21S] to denote the information rate. If a secret sharing scheme is to be practical, we do not want to have to distribute too much secret information as shares. Consequently, we want to make the information rate as high as possible. A secret sharing scheme is perfect if any set of participants in the prohibited structure A obtains no information regarding the master key [6-9]. Secret sharing schemes are classified into the following types.

TYPE I. A secret sharing scheme for the access structure r' is a method of sharing a master key among a finite set of participants in such a way t h a t only subsets of participants in F can recover the master key while other subsets cannot. T h a t is, A ( = 2 P \ F ) is implied.

TYPE II. A secret sharing scheme for the prohibited structure A is a method of sharing a master key among a finite set of participants in such a way t h a t only subsets of participants in A cannot recover the master key while other subsets can. T h a t is, F ( = 2 P \ A ) is implied.

TYPE III. A secret sharing scheme for the mixed structure (F, A) is a m e t h o d of sharing a master key among a finite set of participants in such a way that subsets of participants in F can recover the master key, but subsets of participants in A cannot recover the master key. T h a t is, the privileges of subsets in 2 P \ ( F U A) can be ignored. Any subset of participants in 2 P \ ( F U A) may either recover the master key or not. Note that, here F N A = O, and F U A C 2 P.

Given any access structure F, Ito et al. [1,8] showed t h a t there exists a perfect secret sharing scheme to realize the structure. Benaloh and Leichter [10] proposed a different algorithm to realize secret sharing schemes for any given monotone access structure. In both constructions, the information rate decreases exponentially as a function of n, the number of participants.

There are several performance and efficiency measures proposed for analyzing secret sharing schemes [5,11-14]. Their goal is to maximize the information rate of a secret sharing scheme. Brickell and Stinson [5] studied a perfect secret sharing scheme for graph-based access structure F where the monotone-increasing access structure F contains the pairs of participants corresponding to edges (the prohibited structure is implied to be the collection of subsets of participants corresponding to any independent set of the graph). T h e y proved that, for any graph G with n vertices having maximum degree d, there exists a perfect secret sharing scheme for the access structure based on G in which the information rate is at least 2/(d + 3). Stinson [14] improved the general result t h a t there exists a perfect secret sharing scheme realizing access structure based on G in which the information rate is at least 2/(d + 1). After that, van Dijk [12] showed t h a t Stinson's lower bound is tight because he proved that there exist graphs having maximum degree d such t h a t the optimal information rate is at most 2/(d + 1 - e), for all d _> 3 and E > 0. Secret shar- ing schemes for mixed structures (F, A) proposed by Shieh and Sun in 1994 [15] were based on the graph where F contains the pairs of participants corresponding to edges and A contains the pairs of participants corresponding to nonedges. T h e information rate of their scheme is 1/(2n), where n is the number of participants. In 1996, Sun and Shieh [16] improved the information rate of the secret sharing scheme to be 1/(n - 1).

In this paper, we study the perfect secret sharing scheme for a prohibited structure based on the graph where the monotone-decreasing prohibited structure A contains all participants and the pairs of participants corresponding to edges (the access structure is implied to be the union of {A [ A C P and IA[ _> 3} and the pairs of participants corresponding to nonedges of the graph). We propose an efficient perfect secret sharing scheme for the graph-based prohibited structure. The information rate of our scheme is 2/n, where n is the number of participants. Our scheme can be applied to the reduction of storage and computation loads on the key distribution server in a secure network.

(3)

Graph-Based Prohibited Structures 133 This paper is organized as follows. In Section 2, we give some preliminaries which will be used later on to construct the perfect secret sharing schemes of graph-based prohibited structures. In Section 3, we propose a construction of perfect secret sharing schemes for graph-based prohibited structures. An example of a perfect secret sharing scheme for the graph-based prohibited structure is demonstrated in Section 4. In Section 5, we discuss the application of our construction. Finally, we conclude this paper in Section 6.

2. P R E L I M I N A R I E S

2.1. P e r f e c t (m, n) T h r e s h o l d S c h e m e s

The (m, n) threshold schemes were introduced by Blakley and Shamir in 1979 [3,4]. The main idea underlying an ( m , n ) threshold scheme is to divide the master key K into n shares Si's corresponding to n participants (1 < i < n) in such a way t h a t the master key K cannot be reclaimed unless m shares are collected. Apparently, the (m, n) threshold scheme is the special case of secret sharing schemes when the qualified subsets of participants are all subsets whose order are larger t h a n or equal to m and the nonqualified subsets of participants are all subsets whose order are less t h a n or equal to rn - 1.

A secret sharing scheme is perfect if any unqualified subset of participants provides no infor- mation about the shared secret K [6,8]. It means t h a t the prior probability p ( K = Ko) equals the conditional probability p ( K = Ko given any or less secret shares of an unqualified set). By using the entropy function H from [6,7,9], we can state the requirements for an (m, n) threshold scheme as follows:

(1) H ( K I S i , , . . . , S ~ , ~ ) = 0 ; (2) H ( K [ S ~ , , . . . , S i , , _ l ) = H ( K )

for an arbitrary set of m indices { i l , . . . ,ira} from { 1 , . . . ,n}.

As an example, we review the (m, n) threshold scheme proposed by Shimir [4] as follows. We assume t h a t the master key K is taken randomly from GF(q). Therefore, H ( K ) = log q. Let f ( x ) = am_iX m-1 + . . . + al x + K (rood q) be a polynomial of degree m - 1 over the finite field GF(q). The n share S~'s are computed from f ( x ) as follows:

Si = f ( i ) ( m o d q), i = 1 , . . . , n .

Obviously, given any m secret shares S ~ , . . . , S~,,, { i l , . . . , ira} C { 1 , . . . , n}, f ( x ) can be recon- structed from the Lagrange interpolating polynomial as follows [6]:

Thus, the master key K can be obtained by f(O). On the other hand, given any m - 1 secret shares Si~ , . . . , Si,~_ ~ , { i l , . . . , i r a - l } C { 1 , . . . , n } , f ( O ) can be written as follows:

f(0) = a + S~.,. b(mod q), where

a = E Si~" ~ - k - ~ ) and b = H (r,~--'ij'--)'

k=l j f l j # k j=l

Because S~,~ is uniformly distributed over G F ( q ) , H ( K [ S i l , . . . , S ~ _ I ) =

H(f(O) I &l,

. . . , S~,,,_ ~ ) = H ( a + S~,,, • b) = H ( S~,,, ) = logq = H ( K ) . Therefore, the (re, n) threshold scheme is perfect.

(4)

134 H.-M. SUN A N D S.-P. SHIEH

2.2. Perfect Secret Sharing Schemes for Mixed Structures (r, A)

In this section, we give a construction of perfect secret sharing schemes for mixed structures (F, A), where F = {P} and A = {A [ A C_ P and [A[ < [P[ - 2}. The secret sharing scheme will be used later on to construct the perfect secret sharing schemes for graph-based prohibited structures.

We assume t h a t the master key K = (K1,K2) is taken randomly from G F ( q ) x GF(q). It is clear t h a t H (K) = 2 log q. Let f (x) = an- 1 x n - 1 + . . . + a2x2 + K1 x + 1(2 (mod q) be a polynomial of degree n - 1 over the finite field GF(q). The n shares Sz's are computed from f ( x ) as follows:

Si = f ( i ) ( m o d q), i = 1 , . . . , n .

Obviously, given n secret shares S~, i = 1 , . . . , n, f ( x ) can be reconstructed from the Lagrange interpolating polynomial as follows [6]:

f ( x ) = S k . (mod q).

k--1 j = l , j ~ k

Thus, the master key K can be obtained from f ( x ) . On the other hand, given any n - 2 secret shares S~1,..., S~._2, { Q , . . . , in-2} c { 1 , . . . , n}, we can get the following relations:

• i~ -1 i n - I n - 4 i n - 1 n - 3 i n - 1 • n - 2 i l 1 i n - 4 1 i n - 3 1 in-2 1 a n - 1 a2 K1 K2 S ~ 4

S~,n- 3

(rood q).

Because there are n unknown variables, a n - l , . . . , a2, K1, K2, among these n - 2 equations, it is clear t h a t the total number of possible solutions for K = (K1,/(2) is q2. Hence, H ( K J S~1,..., Si,_2) = H ( K 1 , K 2 J S ~ I , . . . , S i , _ 2 ) = 21ogq = H ( K ) . Therefore, the secret sharing scheme for the mixed structure (F, A) is perfect.

3. C O N S T R U C T I O N O F P E R F E C T S S S F O R P R O H I B I T E D S T R U C T U R E S B A S E D O N G R A P H S

Let P be the set of participants, and G be a graph where a vertex denotes a participant in P and an edge denotes a pair of participants• In a perfect secret sharing scheme for the prohibited structure based of G, a pair of participants corresponding to an edge of G cannot obtain any information regarding the master key. In addition, we also assume t h a t each participant corresponding to a vertex of G cannot obtain any information regarding the master key. This is because t h a t if one participant is allowed to recover the master key by himself, we can assign the master key as his share and remove him from the graph G. The graph we consider here may include disconnected graphs and isolated vertices. A participant corresponding to an isolated vertex can be interpreted as t h a t he can recover the master key in cooperation with any participant in the graph except himself. We use E ( G ) to denote the set of edges of G; E(G) to denote the set of edges of G, where G is the complement of G; S to denote the set of pairs of participants corresponding to edges in E(G); R to denote the set of pairs of participants corresponding to edges in E(G). It is reasonable to restrict t h a t the prohibited structure and the access structure are monotone• Thus, given a graph G, the prohibited structure is denoted by A = {A I A C

(5)

Graph-Based Prohibited Structures 135 P and IA I = 1} U {A I A • S}, and then the access structure is decided by 2 P \ A = {A

IA

c_ P a n d l A I > 3 } U { A I A • R } .

In the following, we will use the conventional threshold schemes [3,4] to construct the perfect secret sharing schemes for graph-based prohibited structures. We assume t h a t all computations are over G F ( q ) where q is a prime.

Given a graph G for the prohibited structure, a perfect secret sharing scheme is constructed as follows. Assume t h a t P = { P l , p 2 , . . . ,P,,} is the set of participants corresponding to the vertices of the graph G. We first construct n + 1 conventional (2, n)-threshold schemes [3,4], named TS1, TS2 . . . . , and TSn+I. To avoid ambiguity, we call the master key and the shares of each T S i submaster key and subshares, respectively. For each (2, n) - T S i , let Ski be its submaster key and si,1, s i , 2 , . . . , si,n be its n subshares. Thus, given any two subshares, si,j and si,k(1 _< j < k < n), the submaster key Ski can be recovered, but less t h a n two subshares provide no information about Ski.

T h e master key of the secret sharing scheme for the prohibited structure based on the graph G is given by K = (K1, K2), which is protected by these submaster keys S k i , S k 2 , . . . , Skn, ,~kn+l in such a way t h a t all n + 1 submaster keys S k i , S k 2 , . . . , Skn, Skn+l collected together, the master key K can be recovered, but any n - 1 or less submaster keys provide no information regarding the master key. It is easy to construct such protection mechanism following the m e t h o d proposed in Section 2.2.

T h e share of participant pi is given by Si = ( a i , 1 , . . . , a i , t , . . . , ai,n, aim+i), where 1 < t < n + 1,

ai,t is e m p t y ai,t = St,i ai,t = Skt ai,t = St,i a~,t = S k t if t = i,

if t = n + 1 and Pt is an isolated vertex, if t = n + 1 and Pt is not an isolated vertex, i f t ~ i , t ~ n + l , and pipt is an edge of G, if t ~ i, t ~ n + 1, and pipt is not an edge of G. Thus, the constructed secret sharing scheme satisfies:

(1) if A E S, A obtains no information regarding the master key,

(2) if A C P and [A[ = 1, A obtains no information regarding the master key, (3) if A E R , A can recover the master key,

(4) if A C_ P and [A I > 3, A can recover the master key.

THEOREM 1. / f A E S, A obtains no information regarding the master key of the constructed secret sharing scheme for the prohibited structure based on the graph G.

PROOF. We assume t h a t A = {pi,pj}, where i ¢ j. T h e share o f p i is Si = (ai,l,ai,2,... ,ai,n+l) and the share o f p j is Sj = ( a j , l , a j , 2 , . . . , a j , n + l ) . Because A • S, Pipj is an edge of G. We conclude t h a t for any t, 1 < t < n + 1, one of the following four cases holds.

(1) ai,t = S k t and aj,t = S k t if t = n + 1, (2) ai,t = e m p t y and aj,t = s t j if t = i, (3) ai,t = st,i and aj,t = e m p t y if t = j ,

(4) ai,t = st# or Skt, and aj,t = std or Skt it t ¢ n + 1,t ~ i, and t ¢ j.

In Cases (1) and (4), the submaster key Skt can be recovered. In Case (2), ai,i and ai,i can obtain only one subshare si,j of the (2, n) - T S i . Therefore, Pi and pj get no information about the submaster key Ski. In Case (3), a~,j and aj,j can obtain only one subshare sj# of the (2, n) - T S i. Therefore, Pi and pj get no information about the submaster key S k i . Hence, Pi and pj can obtain only n - 1 submaster keys which provide no information regarding the master

(6)

136 H.-M. SUN AND S.-P. SHIEH

THEOREM 2. / f A C P and [A[ = 1, A obtains no information regarding the master key of the constructed secret sharing scheme for the prohibited structure based on the graph G.

PROOF. This means the case t h a t each participant obtains no information regarding the master key. We assume t h a t A -- {Pi} and the share o f p i is Si = ( a i , l , a i , 2 , . . . ,ai,n+l). I f p i is not an isolated vertex, then there exists a vertex pj such t h a t Pipj is an edge of G. From Theorem 1, we know t h a t {Pi, Pj } obtains no information regarding the m a s t e r key. Therefore, A = {Pi} obtains no information regarding the m a s t e r key.

If pi is not an isolated vertex, we conclude t h a t for any, t, 1 < t < n + 1, one of the following three cases holds.

(1) ai,t = st# if t = n + l; (2) ai,t = e m p t y if t = i; (3) ai,t = S k t if t ~ n + 1, t ~ i.

In Cases (1) and (2), Pi gets no information a b o u t the s u b m a s t e r key Skn+l and Ski. Hence, Pi can obtain only n - 1 s u b m a s t e r keys which provide no information regarding the master

key K . 1

THEOREM 3. If A 6 R , A can recover the master key of the constructed secret sharing scheme for the prohibited structure based on the graph G.

PROOF. We assume t h a t A = {pi,pj}, where i ¢ j . The share o f p i is Si = (ai,1, a i , 2 , . . . , ai,n+l) and the share of pj is Sj = (ai,1, a33.,..., aj,n+l). Because A E R , PiPj is an nonedge of G. We conclude t h a t for any t, 1 < t < n + 1, one of the following three cases holds.

(1) ai,t = e m p t y and aj,t = Skt if t = i; (2) ai,t : Skt and aj, t = e m p t y if t = j;

(3) ai,t = st# or Skt, and aj,t : 8t,j o r S k t if t ~ i, and t ~ j.

In Cases (1)-(3), the s u b m a s t e r key kt can be recovered. Thus, participant Pi and participant pj can recover all n + 1 s u b m a s t e r keys S k i , S k 2 , . . . , Skn+l, and hence, the m a s t e r key K . | THEOREM 4. iT/A C P and [A[ > 3, A can recover the m a s t e r key of the constructed secret sharing scheme for the prohibited structure based on the graph G.

PROOF. W i t h o u t loss of generality, we assume t h a t A = {Pi,Pi,Pk}, where i, j , and k are distinct. If there exists a pair of participants of A belongs to R , then t h e m a s t e r key can be recovered from T h e o r e m 3. All we need to consider is the case t h a t all PiPj, PiPk, and PiPk are edges of G. From T h e o r e m 1, we know t h a t Pi and pj can recover all s u b m a s t e r keys except Ski and Ski. Similarly, Pi and Pk can recover all submaster keys except Ski and Skk. Also, pj and Pk can recover all s u b m a s t e r keys except Ski and Skk. Therefore, Pi,Pj, and Pk can recover all s u b m a s t e r keys S k i , S k 2 , . . . , Skn+l, and hence, the master key K . l

T h e share of participant pi(= (ai,1,..., a i , t , . . . , ai,n, ai,,~+l)) is an (n + 1)-dimensional vector. Except t h a t ai,i is empty, every ai,j is over GF(q). Therefore, the size of the share is qn. Because the m a s t e r key K is equal to (K1, K2), the size of the m a s t e r key space is q2. It is clear t h a t the information rate of our secret sharing scheme for the graph-based prohibited structure is log q2/log q~ -- 2/n, where n is the number of participants.

4. A N E X A M P L E OF P E R F E C T SSS

F O R A P R O H I B I T E D S T R U C T U R E

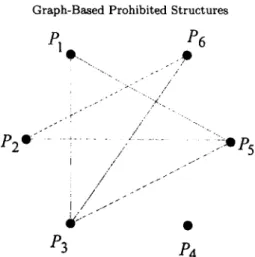
We d e m o n s t r a t e the use of our method in the following example. In Figure 1, the graph G denotes the prohibited structure with six participants. Therefore, E(G) = {PiPs, PiPs, P2Ps, P2Ps, P3Ps, p3Ps } and E(-G) = {piP2, PIP4, PiPs, P2P3, P2P4, P3P4, P4Ps, P4P6, PsP6 }. T h e secret sharing scheme for the prohibited structure based on the graph G is constructed as follows. Let P =

(7)

Graph-Based Prohibited Structures PI P 6 o.. .,o --.. P 2 o- ... i . . . / ," . . . ill ; ? . / ) 5 i j . J " P3 /)4

Figure 1. Graph G with six participants.

137

{Pl, P2, P3, P4, Ps, P6 }. Thus,

S = { { P l , P 3 } , { P l , P 5 } , { P 2 , P 5 } , { P 2 , R 6 } , { R 3 , P 5 } , { R 3 , P 6 } } , and

R =

The prohibited structure

A = ~¢~p1}~p2}~p3}~p4}~{p5}~p6}~pbp3}~{p1~p5}~p2~p5}~{p2~p6~p3~p~}'~p3~p6}}.

The access structure

F : { { R I , p 2 } , { P l , P 4 } , { R I , P 6 } , { P 2 , p 3 } , { p 2 , p 4 } , { P 3 , R 4 } , { R 4 , P 5 } , { p 4 , P 6 } { R 5 , P 6 ) , {Pl,P2,P3},{Pl,P2,P4},{Pl,P2,PS},{BI,P2,P6},{Pl,P3,P4},{Pl,P3,Ps}, {P2,P3,P6},{P2,Pa,PS},{P2,P4,R6},{P2,P~,P6},{P3,P4,PS},{P3,P4,P6}, {Pl, P2, P4, P5 }, {Pl, P2, P4, P6 }, {Pl, P2, PS, P6 }1 {Pl, P3, P4, P5 }, {Pl, P3, P4, P6 }, {Pl , P3, P5, {P2,P4,Ps, {Pl,P2,P3, {Pl,P2,P3,

p6},{pl,v4,ps,p6},{ ,p3,v4,vs},{p2,p3,v4,v6},{v2,p3,vs,p },

P6}, {P3,P4,Ps,P6}, {Pl,P2,P3,P4,Ps}, {Pl,P2,P3,P4,P6}, Ps,P6},{Pl,P2,Pa,Ps,P6},{Pl,P3,P4,Ps,P6},{P2,P3,P4,Ps,P6},

Let TS1, T S 2 , . . . , and TS7 be seven (2,6)-threshold schemes. We assume that Ski is the

submaster key of T S i and s~,l, si,2,..., and si,6 are the subshares of TSi, for 1 < i < 7. Here we

use Shamir's method [4] to construct these threshold schemes. For each (2, 6) - TSi, let

f i ( x ) = ri . x + Ski(mod q)

be a secret polynomial of degree 1 over the finite field GF(q), where q is a prime. Let I D j denote

the identity of the participant pj. The six subshares si,1,...,si,6 are computed from f~(x) as

follows:

si,j = f i ( I D j ) ( m o d q), j = 1 . . . . ,6.

Obviously, given any two subshares, si,j and si,k, f i ( x ) can be reconstructed from the Lagrange

interpolating polynomial as follows [6]:

(x - IDk) (x - I D j ) (mod q).

(8)

Thus, the submaster key

Ski(=

f~(0)) can be obtained, but less than two subshares provide no information about the submaster key.

The master key of the secret sharing scheme is given by K = (K1, K2) which is protected by these submaster keys

Ski, Sk2,... ,Sk7

in such a way that all seven submaster keys collected together, the master key K can be recovered, but any five or less submaster keys provide no information regarding the master key (see Section 2.2.). The shares of participants are given by:

S1 = (--, Sk2, s3,1, Sk4, s5,1, Sks, SkT)

$2 = (Ski,--, Sk~, Sk4, s5,2, s6,2, SkT)

$3 = <s1,3,

Sk2,--, Sk4,

s5,3,

s6,3, SkT>

$4 = (Ski, Sk2, Sk3,--, Sk5, Sks,

87,4)

$5 = (s,,s,

s2,5, s3,5, Sk4,--, Sks, Sk~>

$6 = (Ski, s2,6, s3,6, Sk4, Sks,--, SkT>

where ' - - ' , denotes e m p t y entry.

In the following, we demonstrate the constructed secret sharing scheme satisfies: (1) if A E S, A obtains no information regarding the master key;

(2) if A C_ P and [A[ = 1, A obtains no information regarding the master key; (3) if A E R , A can recover the master key;

(4) if A C_ P and [A[ > 3, A can recover the master key.

If A --- {Pl,P3} E A, A cannot recover

Ski

and

Sk3.

Therefore, A obtains no information about the master key K .

If A = {P4} E A, A cannot recover

Sk4

and

SkT.

Therefore, A obtains no information about the master key K .

If

A -- {Pl,p2} E

F, A can recover the master key K as follows.

(1) Participant PI can obtain

Sk2, Sk4, Sks,

and

Sk7

because he owns his share $1. (2) Participant P2 can obtain

Ski, Sk3, Sk4,

and

Sky

because he owns his share $2. (3) Participants Pl and P2 can recover

Sk5

from as,1 of S1 and s5,2 of $2.

Therefore, participants Pl and P2 can recover all seven submaster keys, and hence, the master key K.

If A = {Pl,P3,Ps} E F, A can recover the master key K as follows.

(1) Participant Pl can obtain

Sk2, Sk4, Sks,

and

Sk7

because he owns his share $1. (2) Participants P3 and Ps can recover

Ski

from Sl,3 of $3 and sl,s of Ss.

(3) Participants Pl and Ps can recover Sk3 from s3,1 of S1 and s3,s of $5. (4) Participants Pl and P3 can recover

Sks

from ss,1 of $1 and s5,3 of $3.

Therefore, participants Pl, P3, and Ps can recover all seven submaster keys, and hence, the master key K.

5. A P P L I C A T I O N

Our secret sharing scheme for graph-based prohibited structures can be employed in many applications in various areas, such as secure communication networks, and secure databases. It is particularly useful for access control (e.g., reading a file, or sending a message) in an environment where the number of participants is large, such as a large secure network. Consider a network system with n participants, where an access control policy is enforced by a Communication Granting Server (CGS) to restrict the communication between participants. A secure session key will be issued unless the sender requesting the key is allowed to communicate with the receiver. The access control matrix employed in conventional access control mechanisms can be used by the C G S to achieve the goal [17]. However, the C G S needs to store and search the large access control matrix of size O(n2). This size of information causes heavy storage and computation

(9)

Graph-Based Prohibited Structures 139 loads on t h e C G S w h e n n is large. I n t h e worst case, t h e storage a n d c o m p u t a t i o n loads m a y m a k e this design impractical.

I n c o n t r a s t , t h e secret sharing scheme for g r a p h - b a s e d p r o h i b i t e d s t r u c t u r e s is m o r e efficient. We can t r a n s f o r m t h e c o m m u n i c a t i o n relationships into a graph, where a v e r t e x denotes a par- t i c i p a n t a n d an edge does an illegal c o m m u n i c a t i o n . In t h e n e t w o r k system, each p a r t i c i p a n t holds a secret (e.g., his password). T h e secret can be t r a n s f o r m e d into t h e c o r r e s p o n d i n g share in t h e secret s h a r i n g scheme b y t h e c o m m u n i c a t i o n g r a n t i n g server. T h e t r a n s f o r m a t i o n needs to be o n e - w a y so t h a t it is c o m p u t a t i o n a l l y infeasible to c o m p u t e t h e secret f r o m t h e share. T w o p a r t i c i p a n t s present their secrets t o t h e C G S w h e n a t t e m p t i n g t o c o m m u n i c a t e . If t h e two corre- s p o n d i n g shares g e n e r a t e d b y t h e two secrets c a n successfully d e t e r m i n e t h e m a s t e r key, t h e C G S will r e t u r n a session key t o b o t h participants. This session key will be used as b o t h e n c r y p t i o n a n d d e c r y p t i o n keys for f u t u r e c o m m u n i c a t i o n between these two participants. I n t h e scheme, t h e C G S need n o t m a i n t a i n a large access control matrix, b u t only needs t o keep a single m a s t e r key.

6. C O N C L U S I O N S

I n this paper, we give a c o n s t r u c t i o n of perfect secret sharing schemes for mixed s t r u c t u r e s (F, A ) , where F = ( P } a n d A = ( A [ A C_ P a n d IAI <_ IPI - 2). Based on t h e p r o p o s e d perfect secret s h a r i n g schemes, we p r o p o s e an efficient c o n s t r u c t i o n of a perfect secret sharing scheme for g r a p h - b a s e d p r o h i b i t e d s t r u c t u r e s where a vertex denotes a p a r t i c i p a n t a n d an edge denotes a pair of p a r t i c i p a n t s w h o c a n n o t recover t h e m a s t e r key. T h e i n f o r m a t i o n r a t e of o u r scheme is 2 / n , where n is t h e n u m b e r of participants. We also present an application of o u r scheme to t h e reduction of storage a n d c o m p u t a t i o n loads o n the c o m m u n i c a t i o n granting server in a secure network.

R E F E R E N C E S

i. M. Ito, A. Saito and T. Nishizeki, Secret sharing scheme realizing general access structure, In Proceeding of I E E E Globecom '87, Tokyo, pp. 99-102, (1987).

2. W.A. Jackson, K.M. Martin and C.M. O'Keefe, Multisecret threshold schemes, In Advances in Cryptology- Crypto '93 Proceedings, Lecture Notes in Computer Science, Volume 773, pp. 126-135, Springer-Verlag, Berlin, (1994).

3. G.R. Blakley, Safeguarding cryptographic keys, In Proceeding of AFIPs 1979 National Computer Con]erence, New York, Volume 48, pp. 313-317, (1979).

4. A. Shamir, How to share a secret, Commun. of the ACM 22 (11), 612-613, (1979).

5. E.F. Brickell and D.R. Stinson, Some improved bounds on the information rate of perfect secret sharing schemes, Journal of Cryptology 5, 153-166, (1992).

6. D.E.R. Denning, Cryptography and Data Security, Addison-Wesley, Reading, MA, (1983). 7. R.W. Hamming, Coding and Information Theory, Prentice-Hall, Englewood Cliffs, N J, (1986).

8. M. Ito, A. Saito and T. Nishizeki, Multiple assignment scheme for sharing secret, Journal of Cryptolog~ 6, 15-20, (1993).

9. C.E. Shannon, Communication theory of secrecy systems, Computer Security Journal Vl (2), 7-66, (1990). 10. J. Benaloh and J. Leichter, Generalized secret sharing and monotone functions, In Advance8 in Cryptology- Crypto'88 Proceedings, Lecture Notes in Computer Science, Volume 403, pp. 27-35, Springer-Verlag, Berlin, (1990).

11. R.M. Capocelli, A. DeSantis, L. Gargano and U. Vaccaro, On the size of shares for secret sharing schemes, In Advances in Cryptology-Crypto'91 Proceeding, Lecture Notes in Computer Science, pp. 101-113, Springer- Verlag, Berlin, (1992).

12. M. van Dijk, On the information rate of perfect secret sharing schemes, Designs, Codes and Cryptography 6, 143-169, (1995).

13. D.R. Stinson, New general lower bounds on the information rate of secret sharing schemes, In Advance in Cryptology-CRYPTO'9~, Lecture Notes in Computer Science, Volume 740, pp. 168-182, (1993).

14. D.R. Stinson, Decomposition constructions for secret sharing schemes, IEEE Trans. Inform. Theory 40 (1), 118-125, (1994).

15. S.P. Shieh and H.M. Sun, On constructing secret sharing schemes, In Proceedings of the 1994 IEEE Interna- tional Conference of Computer Communications, Networking for Global Communications (INFOCOM'9~), pp. 1288-1292, (1994).

(10)

16. H.M. Sun and S.P. Shieh, A n efficient construction of perfect secret sharing schemes for graph-based struc- tures, Computers Math. Applic. 31 (7), 129-135, (1996).

17. B.W. Lampson, Protection, In Proceeding of the 5 th Princeton STrop. of Info. Sci. and Syst., Princeton Univ., pp. 437-443, (March 1971); Reprinted in A C M Oper. Svst. Rev. 8 (1), 18-24, (January 1994).