迪菲方塊 - 政大學術集成

全文

(1)國立政治大學應用數學系數學教學碩士在職專班. 政治大立 DIFFY PENTAGON. 學 ‧. ‧ 國. 碩士學位論文. n. er. io. sit. y. Nat. al. Ch. engchi. i Un. v. 碩專班學生：黃信弼撰. 指導教授：李陽明中華民國. 101. 年. 8. 博士月. 24 日.

(2) Contents. Abstract. i. 中文摘要. ii. Chapter 1. Introduction. 1. Chapter 2 The Description of the Convergence Properties 2.1 Definitions and Theorems. 立. 2. 政治大. 2. 2.2 Description of Feature. 8. ‧ 國. 學. Chapter 3 Pentagon with Cycle Convergence. ‧ y. 11. sit. io. al. n. 3.2 The Proof with Strong Induction. Chapter 4 Conclusion and Promotion. Ch. er. Introduction. Nat. 3.1. 11. n engchi U. iv. 11. 23. Appendix. 24. References. 26.

(3) Diffy Pentagon Abstract In Diffy box, we write down numbers on the four vertices of square, and then on the midpoint of each side write the difference between the two numbers at its endpoints. numbers on the four vertices of a square will converge to zero finally.. It is known that the. In this article, we use the. same operations as Diffy box to discuss pentagons which we call" Diffy pentagon ". converge, too.. 政治大. Diffy pentagon, Strong induction. 立. 學 ‧. ‧ 國 io. sit. y. Nat. n. al. er. Keywords:. Ch. engchi. i. i Un. v. We find it will.

(4) 迪菲五邊形中文摘要在迪菲方塊中，我們將正方形的四個頂點皆填入數值，再利用相鄰兩頂點相減，再取絕對值的方式觀察其數列行為，發現四個頂點的數字最後皆會收斂至 0。在本文中，我們將之推廣至五邊形，我們稱它為迪菲五邊形。我們套用同樣的運算模式後，發現亦有特殊的收斂行為。迪菲五邊形、強勢數學歸納法. 立. 政治大. 學 ‧. ‧ 國 io. sit. y. Nat. n. al. er. 關鍵字：. Ch. engchi. ii. i Un. v.

(5) Chapter 1. Introduction. Diffy box, also called difference box, is a simple method that provide us subtraction practice. The idea’s original author is unknow, we could only trace back to Professor Juanita Copley of the University of Houston who has introduced it as a problem-solving activity in professional development sessions.. To create a Diffy box is as follows:. 政治大 On the midpoint of each side write the difference between the two numbers at its endpoints. 立. 1. Draw a square, and label each vertex with a ( rational ) number. 2.. ‧ 國. 學. 3. Inscribe a new square in the old one, using these new numbers to label the vertices. 4. Repeat this process, and continue inscribing new boxes until reaching a square that has all four. ‧ y. Nat. n. al. And here, we use the same operations as Diffy box to. er. io. In Diffy box, we only consider squares.. sit. vertices labeled 0.. i Un. v. discuss pentagons which we call" Diffy pentagon." We try to find its convergence laws.. Ch. engchi. 1.

(6) Chapter 2. The Description of the Convergence Properties. 2.1 Definitions and Theorems. Definition 2.1. Let a,b,c,d,e be nonnegative integers, we define an ordered set. five vertices of the regular-pentagon, and another ordered set. (a b c d e) be the. )a b c d e( be the five vertices of. the anti-pentagon.. 治政 Note that we often use the first element of the ordered set (a大 b c d e) to be the upper left of the 立 regular-pentagon, and in clockwise order. Also, we use the first element of the ordered set ‧ 國. 學. )a b c d e( to be the upper left of the anti-pentagon, and in clockwise order.. ‧. )a b c d e( on the anti-pentagon as in. n. al. sit. io. Figure 2.2.. And an ordered set. er. regular-pentagon as in Figure 2.1.. Figure 2.1:. Definition 2.2. (a b c d e) on the. y. Let a,b,c,d,e be nonnegative integers, we take an ordered set. Nat. Example 2.1. Ch. engchi. Regular-pentagon. i Un. v. Figure 2.2:. We define the child of an ordered set. )│a－b│ │b－c│ │c－d│ │d－e│ │e－a│( and │c－d│ │d－e│ │e－a│( ( see Figure 2.3).. 2. Anti-pentagon. (a b c d e) to be the ordered set. (a b c d e) a parent of. )│a－b│ │b－c│.

(7) Also, we define the child of an ordered set │b－c│ │c－d│ │d－e│) and. )a b c d e( to be the ordered set. )a b c d e( a parent of. (│e－a│ │a－b│. (│e－a│ │a－b│ │b－c│ │c－d│. │d－e│) ( see Figure 2.4). And write their relation as parent  child.. The first pentagon is the parent, and the second pentagon is the child.. 立. ‧. ‧ 國. 學. The first pentagon is the parent, and the second pentagon is the child.. io. sit. y. Nat. Figure 2.4:. 政治大. er. Figure 2.3:. It is easy to see if we rotate both anti-pentagon and its child ( see Figure 2.4) counterclockwise 360. al. n. iv n C through the center, we obtain the regular-pentagon child ( see Figure 2.5), and vice versa. h e n gandc its hi U. Figure 2.5: Since (a b c d e) and distinguish between them. or. )a b c d e(. differ by a rotation of 360, sometimes, we don’t want to. For convenience, we define an ordered set [a b c d e] to be (a b c d e). )a b c d e( . 3.

(8) Definition 2.3. For any [a1 b1 c1 d1 e1]  [a2 b2 c2 d2 e2]  [a3 b3 c3 d3 e3]  ....  [at bt ct dt et]  ...  [ak bk ck dk ek] ...If there exists one [ak bk ck dk ek] = [at bt ct dt et], for. the smallest t, k, and k > t, then we call [at bt ct dt et]  ...  [ak－1 bk－1 ck－1 dk－1 ek－1]  [ak bk ck dk ek] the cycle convergence of [a1 b1 c1 d1 e1]. Example 2.2. Take a pentagon with [3 1 2 4 1], find its cycle convergence.. Solution : Since [3 1 2 4 1] . (1). [0 1 1 1 1]. (3). (2). 學. ‧ 國. 立. 治政 [2 1 2 3 2] 大.  [1 0 0 0 1]. ‧.  [0 1 0 0 1]. (5) (6). sit. y. Nat.  [1 1 0 1 1]. (4). io. er. Since the ordered set (3) is equal to (6), by Definition 2.3, we take t = 3 and k = 6, and then call [0 1 1 1 1]  [1 0 0 0 1]  [0 1 0 0 1]  [1 1 0 1 1] = [0 1 1 1 1] the cycle convergence of. n. al. [3 1 2 4 1].. Definition 2.4 [a b c d e]. . Definition 2.5. Ch. engchi. i Un. v. [a b c d e] is isomorphic to [a' b' c' d' e'] and denoted by [a' b' c' d' e'] if they have the same child.. [a b c d e] and [a' b' c' d' e'] are similar and denoted by [a b c d e] 〜 [a' b' c' d' e']. if i' = ki, where i  {a, b, c, d, e}, k is a nonzero integer.. 4.

(9) Example 2.3. Two pentagons : [3 1 2 4 1] and [3k k 2k 4k k], k be any positive integer.. Find their. cycle convergences.. Solution : Since [3 1 2 4 1]. Since [3k k 2k 4k k]. . [2 1 2 3 2]. . [2k k 2k 3k 2k]. . [0 1 1 1 1]. . [0 k k k k]. . [1 0 0 0 1]. . [k 0 0 0 k]. . [0 1 0 0 1]. . [0 k 0 0 k]. . [1 1 0 1 1]. 政治大. 立. [k k 0 k k]. Since the ordered set [0 1 1 1 1] is equal to [1 1 0 1 1],. ‧ 國. 學. [0 1 1 1 1]  [1 0 0 0 1]  [0 1 0 0 1]  [1 1 0 1 1] = [0 1 1 1 1] is the cycle convergence of. ‧. [3 1 2 4 1].. y. Nat. Since the formula [0 k k k k] is equal to [k k 0 k k],. n. al. er. io. [3k k 2k 4k k].. sit. [0 k k k k]  [k 0 0 0 k]  [0 k 0 0 k]  [k k 0 k k] = [0 k k k k] is the cycle convergence of. Ch. engchi. i Un. v. Note that they have the same kind of cycle convergences which just need to multiply each component number by k .. Theorem 2.1. For any [a b c d e], where a, b, c, d, e are nonnegative integers with a = b = c = d =. e, then the child of the pentagon is [0 0 0 0 0].. 5.

(10) Proof : Since a = b = c = d = e, [a b c d e]  [│a－b│ │b－c│ │c－d│ │d－e│ │e－a│] = [0 0 0 0 0] And the proof is complete.. Theorem 2.2. Let a, b, c, d, e be any nonnegative integers, and k be any integer, then [a b c d e]. and [a+k b+k c+k d+k e+k] are isomorphic.. Proof :. 治政 It is easy to see [a b c d e]  [│a－b│ │b－c│ │c－d│ │d－大e│ │e－a│] 立 and [a+k b+k c+k d+k e+k]  [│a－b│ │b－c│ │c－d│ │d－e│ │e－a│] ‧ 國. 學. Since they have the same child. sit. y. Nat. Theorem 2.3. [a+k b+k c+k d+k e+k].. For any [a b c d e], a, b, c, d, e be any nonnegative integers, and a, b, c, d, e are not. io. er. . ‧. [a b c d e]. al. all equal, if one of its child is as [0 0 0 n n] or [0 0 n 0 n] or [n 0 n n n] for some positive n, then it. n. iv n C must have a cycle convergence constitutedh by [0 0 0 n n], [0 0Un 0 n], and [n 0 n n n], in cyclic engchi order.. Proof : First, we make a relation with [0 0 0 n n], [0 0 n 0 n], and [n 0 n n n]. Let [0 0 0 n n] be a regular-pentagon, then its child is [0 0 n 0 n], and then its child is [n 0 n n n], and then its child is [n n 0 0 0]. ( see Figure 2.6) 6.

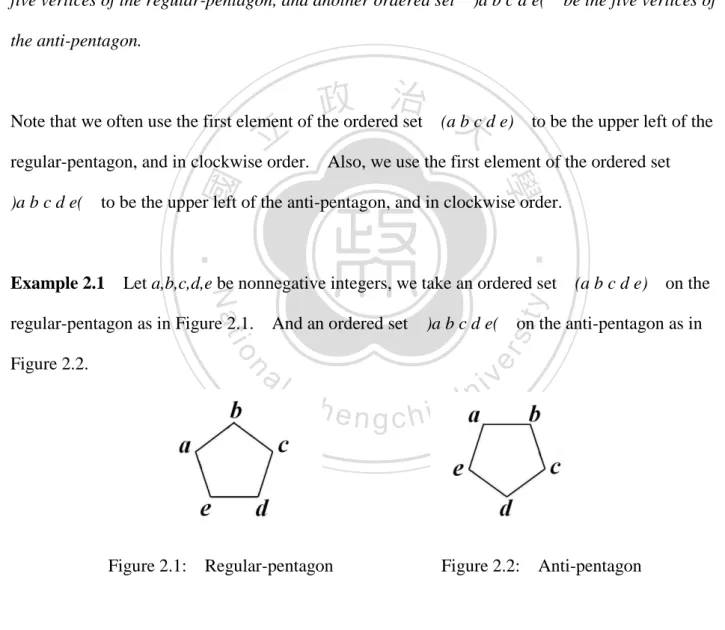
(11) Figure 2.6:. The first pentagon is [0 0 0 n n], and then [0 0 n 0 n], and then [n 0 n n n], and then [n n 0 0 0].. Since [a b c d e] is a cycle order pentagon, it is easy to see [n n 0 0 0] = [0 0 0 n n] by a cyclic rotation, and similarly for [0 0 n 0 n] and [n 0 n n n], thus the theorem hold for regular-pentagons. Next, let [0 0 0 n n] be an anti-pentagon.. 立. Then its child is [n 0 0 n 0 ],. 政治大. ‧ 國. 學. and then its child is [n 0 n n n], and then its child is [0 n n 0 0]. ( see Figure 2.7). ‧. n. al. er. io. sit. y. Nat Figure 2.7:. Ch. i Un. v. The first pentagon is [0 0 0 n n], and then [n 0 0 n 0],. engchi. and then [n 0 n n n], and then [0 n n 0 0].. Since [a b c d e] is a cycle order pentagon, it is easy to see [0 n n 0 0] = [0 0 0 n n] by a cyclic rotation, and similarly for [0 0 n 0 n] and [n 0 n n n], thus the theorem holds in anti-pentagons. Therefore, if one child of any cycle order pentagon as [0 0 0 n n], [0 0 n 0 n], or [n 0 n n n], then it must have a cycle convergence which is constituted by [0 0 0 n n], [0 0 n 0 n], and [n 0 n n n], in cyclic order.. 7.

(12) Remark 2.1. For any [a b c d e] and [a' b' c' d' e'], where a, b, c, d, e, a', b', c', d', e' are. nonnegative integers, and a, b, c, d, e are not all equal, and a', b', c', d', e' are not all equal, either. If [a b c d e]. . [a' b' c' d' e'], and one of them has a cycle convergence, then the other must has. the same cycle convergence.. Theorem 2.4. If. 0 ≦ a ＜ M and 0 ≦ b ＜ M, then 0 ≦. |a – b| ＜ M.. Proof : Since 0 ≦ a ＜ M. 0 ≦ b ＜ M. and. 0–M ＜ a–b ＜ M–0. . –M ＜ a–b ＜ M. . 0 ≦. ‧ 國. |a – b| ＜ M. ‧. Description of Feature. n. al. er. io. sit. y. Nat. 2.2. 立. 學. . 政治大. Ch. i Un. v. In our study, we find that for any [a b c d e], where a, b, c, d, e are all nonnegative integers and not. engchi. all equal, then its child must make a cycle convergence as the following figure, where n is any positive integer.. Next, we will take an example to show this feature. 8.

(13) Example 2.4. Take a pentagon with [5 3 2 1 3], please find its cycle convergence.. Solution : Since [5 3 2 1 3]  [2 1 1 2 2]  [0 1 0 1 0]  [1 1 1 1 0]  [1 0 0 0 1]  [1 0 0 1 0] = [0 1 0 1 0]. By this feature, we say. 立. 政治大. is the cycle convergence of the pentagon with [5 3 2 1 3].. 學. ‧ 國. [0 1 0 1 0]  [1 1 1 1 0]  [1 0 0 0 1]  [1 0 0 1 0] = [0 1 0 1 0]. ‧. io. er. [n 0 n n n] = [1 1 1 1 0], and [0 0 0 n n] = [1 0 0 0 1].. sit. y. Nat. Note that if we rotation with these three pentagons and let n = 1, we will get [0 0 n 0 n] = [0 1 0 1 0],. al. At next section, we prove for any [a b c d e] of pentagon, a, b, c, d, e be any nonnegative integer,. n. iv n C and a, b, c, d, e are not all equal, then [a b h c d e] must have aU e n g c h i cycle convergence which constituted by [0 0 0 n n], [0 0 n 0 n], and [n 0 n n n] for some positive natural number n. For convenience, we call:. [0 0 0 n n]. is typeⅠ. [0 0 n 0 n]. is typeⅡ. [n 0 n n n]. is typeⅢ. 9.

(14) And by Theorem 2.3, we get for any pentagon, if one of its child is as like as typeⅠor typeⅡor typeⅢ, then it must have a cycle convergence as:. typeⅠ  typeⅡ  typeⅢ  typeⅠ or typeⅡ  typeⅢ  typeⅠ  typeⅡ or typeⅢ  typeⅠ  typeⅡ  typeⅢ. And all cycle convergences just have three ordered sets.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 10. i Un. v.

(15) Chapter 3. Pentagon with Cycle Convergence. 3.1 Introduction. Let [a b c d e] be a cycle order pentagon, a, b, c, d, e are all nonnegative integers and not all equal, and let m = min{a, b, c, d, e}, then at least one element of [a－m, b－m, c－m, d－m, e－m] must be zero.. 政治大 [a b c d e], and it is easy to see if one of them has a cycle. Since [a－m, b－m, c－m, d－m, e－m] and [a b c d e] have the same child, by Theorem 2.2, [a－m, b－m, c－m, d－m, e－m].  立. ‧ 國. [a－m, b－m, c－m, d－m, e－m] has a cycle convergence.. So we just need to prove. 學. convergence, the other must have the same cycle convergence, too.. ‧. Nat. n. sit er. io. al. y. 3.2 The Proof with Strong Induction. Ch. i Un. v. We let [a b c d e] be a cycle order pentagon again, and assume at least one element of a, b, c, d, e be zero.. engchi. By strong induction to prove cycle convergence, we check the following pentagons first:. 1. [1 0 0 0 0]  [1 0 0 0 1] = [0 0 0 1 1] (typeⅠ). 2. [1 1 0 0 0] = [0 0 0 1 1] (typeⅠ). 11.

(16) 3. [1 0 1 0 0] = [0 0 1 0 1] (typeⅡ). 4. [1 1 1 0 0]  [0 0 1 0 1] (typeⅡ). 立. 政治大. ‧ 國. 學 ‧. 5. [1 1 0 1 0]  [0 1 1 1 1] = [1 0 1 1 1] ( typeⅢ). n. er. io. sit. y. Nat. al. 6. [1 1 1 1 0] = [1 0 1 1 1] ( typeⅢ). Ch. engchi. i Un. v. And then, we assume for any pentagon must have cycle convergence if the value of max{a, b, c, d, e} equal 1,2,3,〃〃〃,M－1. Finally, we just need check if the value of max{a, b, c, d, e} equal M, then the pentagon still has cycle convergence, too. 12.

(17) To check this, assume that n is the number of M’s and t is the number of 0’s in a, b, c, d, e. the remaining elements of pentagon, we call x, y, z , and let 0 < x, y, z < M.. We let. And then, classify with. the numbers of elements of " M " and " 0 " as the following cases:. ■ Case 1. Let n = 1, and t = 1, (1):[M 0 x y z] [M 0 x y z]  [M x |x－y| |y－z| M－z] Let a = |x－y| , b = |y－z| , c = M－z ,. 治政 Since 0 < x, y, z < M, and 0 < c < M, by Theorem 2.4, 0 ≦ 大a, b ＜ M. 立 And then [M x |x－y| |y－z| M－z] = [M x a b c]  [M－c M－x |x－a| |a－b| |b－c|] ‧ 國. 學. By Theorem 2.4, 0 ≦ |x－a|, |a－b|, |b－c| ＜ M and since 0 ≦ M－x, M－c ＜ M,. n. al. er. io. sit. y. Nat. And then, [M 0 x y z] has cycle convergence, too.. ‧. [M－c M－x |x－a| |a－b| |b－c|] must have cycle convergence.. Ch. engchi. i Un. v. (2):[M x 0 y z] [M x 0 y z]  [M－x x y |y－z| M－z] Since 0 < y, z ＜ M, by Theorem 2.4, 0 ≦ |y－z| ＜ M. Since 0 < M－x, x, y, M－z ＜ M, [M－x x y |y－z| M－z] must have cycle convergence. And then, [M x 0 y z] has cycle convergence, too.. 13.

(18) ■ Case 2. Let n = 1, and t = 2, (1): [M 0 0 x y] [M 0 0 x y]  [M 0 x |x－y| M－y] (a) If x≠y : By case 1 (1), [M 0 x |x－y| M－y] has cycle convergence. And then, [M 0 0 x y] has cycle convergence, too. (b) If x = y : [M 0 x |x－y| M－y] = [M 0 x 0 M－x]  [x M x x M－x]  [M－x M－x 0 |M－2x| |M－2x|]. Since 0 < M－x, x < M, by Theorem 2.4, 0 ≦ |M－2x| ＜ M.. 治政 Therefore, [M－x M－x 0 |M－2x| |M－2x|] must 大 have cycle convergence. 立 And then, [M 0 0 x y] has cycle convergence, too. ‧. ‧ 國. 學. al. er. io. sit. y. Nat. (2): [M 0 x 0 y]. v. n. [M 0 x 0 y]  [M x x y M－y]  [y M－x 0 |x－y| |M－2y|]. Ch. engchi. i Un. Since 0 < M－y, x, y ＜ M, by Theorem 2.4, 0 ≦ |M－2y|, |x－y| ＜ M. Since 0 < M－x < M, [y M－x 0 |x－y| |M－2y|] must have cycle convergence. And then, [M 0 x 0 y] has cycle convergence, too.. (3): [M 0 x y 0] [M 0 x y 0]  [M x |x－y| y M] Let a = |x－y|, since 0 < x, y < M, by Theorem 2.4, 0 ≦ a < M. 14.

(19) So [M x |x－y| y M] = [M x a y M]  [0 M－x |x－a| |y－a| M－y] Since 0 ≦ a < M and 0 < x, y < M, by Theorem 2.4, 0 ≦ |x－a|, |y－a| < M Since 0 < M－x, M－y < M, [0 M－x |x－a| |y－a| M－y] must have cycle convergence. And then, [M 0 x y 0] has cycle convergence, too.. (4): [M x 0 0 y]. 立. [M x 0 0 y]  [M－x x 0 y M－y]. 政治大. ‧ 國. 學. Since 0 < M－x, M－y, x, y < M, [M－x x 0 y M－y] must have cycle convergence. And then, [M x 0 0 y] has cycle convergence, too.. ‧. n. al. er. io. sit. y. Nat. ■ Case 3. Let n = 1, and t = 3,. Ch. engchi. i Un. v. (1):[M 0 0 0 x] [M 0 0 0 x]  [M 0 0 x M－x] Since 0 < M－x < M, by case 2 (1), [M 0 0 x M－x] has cycle convergence. And then, [M 0 0 0 x] has cycle convergence, too.. (2): [M 0 0 x 0] 15.

(20) [M 0 0 x 0]  [M 0 x x M]  [0 M x 0 M－x] Since 0 < x < M  0 < M－x < M, by case 2 (2), [0 M x 0 M－x] has cycle convergence. And then, [M 0 0 x 0] has cycle convergence, too.. ■ Case 4. Let n = 1, and t = 4, (1):[M 0 0 0 0] [M 0 0 0 0]  [M 0 0 0 M]. 政治大  typeⅠ 立 ‧. ‧ 國. 學. So [M 0 0 0 0] has cycle onvergene.. n. al. er. io. sit. y. Nat. ■ Case 5. Let n = 2, and t = 1,. Ch. (1):[M M 0 x y]. engchi. i Un. v. [M M 0 x y]  [0 M x |x－y| M－y] (a) If x≠y : Since 0 < x, y < M, by theorem2.4, 0 < |x－y| < M. By case 1 (1), [0 M x |x－y| M－y] has cycle convergence. And then, [M M 0 x y] has cycle convergence, too. (b) If x = y : [0 M x |x－y| M－y] = [0 M x 0 M－x] : Since 0 < M－x < M, by case 2 (2), [0 M x 0 M－x] has cycle convergence. And then, [M M 0 x y] has cycle convergence, too.. 16.

(21) (2):[M M x 0 y] [M M x 0 y]  [0 M－x x y M－y] Since 0 < M－x, M－y, x, y < M, [0 M－x x y M－y] has cycle convergence. And then, [M M 0 x y] has cycle convergence, too.. 立. 政治大. ‧ 國. 學. (3): [M 0 M x y]. [M 0 M x y]  [M M M－x |x－y| M－y]. ‧. (a) If x = y : [M M M－x |x－y| M－y] = [M M M－x 0 M－x]. y. Nat. io. sit. Since 0 < M－x < M, by case 5 (2), [M M M－x 0 M－x] has cycle convergence.. n. al. er. And then, [M 0 M x y] must have cycle convergence, too. (b) If x≠y : Let k = min{ M－x, |x－y|, M－y }. Ch. e ng c h i. Then [M M M－x |x－y| M－y]. i Un. v. [ M－k M－k M－x－k |x－y|－k M－y－k]. Since at least one element of M－x－k, |x－y|－k, M－y－k is zero and all elements of M－k, M－x－k, |x－y|－k, M－y－k are smaller then M. It means [M－k M－k M－x－k |x－y|－k M－y－k] has cycle convergence. And then, [M 0 M x y] has cycle convergence, too.. 17.

(22) (4): [M x M 0 y] [M x M 0 y]  [M－x M－x M y M－y] Since 0 < x, y < M, we get 0 < M－x, M－y < M Let k = min{ M－x, M－y, y}.  [ M－x－k M－x－k M－k y－k M－y－k]. Then [M－x M－x M y M－y]. Since at least one element of M－x－k, y－k, M－y－k is zero and all elements of M－x－k, M－k, y－k, M－y－k are smaller then M, it means [M－x－k M－x－k M－k y－k M－y－k] has cycle convergence.. And then, [M x M 0 y] has cycle convergence, too.. 立. ‧ 國. ‧ y. sit. al. n. [M M 0 0 x]  [0 M 0 x M－x]. er. io. (1): [M M 0 0 x]. Nat. Let n = 2, and t = 2,. 學. ■ Case 6.. 政治大. Ch. engchi. By case 2 (3), [0 M 0 x M－x] has cycle convergence. And then, [M M 0 0 x] has cycle convergence, too.. (2): [M M 0 x 0] [M M 0 x 0]  [0 M x x M] By case 5 (3) : [0 M x x M] has cycle convergence. And then, [M M 0 x 0] has cycle convergence, too. 18. i Un. v.

(23) (3): [M 0 M 0 x] [M 0 M 0 x]  [M M M x M－x]  [x 0 0 M－x |M－2x|] Since 0 < x, M－x < M, by Theorem 2.4, 0 ≦ |M－2x| < M. And since 0 ≦ x, M－x, |M－2x| < M, [x 0 0 M－x |M－2x|] has cycle convergence. And then, [M 0 M 0 x] has cycle convergence, too.. 政治大. 立. ‧. ‧ 國. 學. (4): [M x M 0 0]. [M x M 0 0]  [M－x M－x M 0 M]. y. Nat. n. al. Ch. engchi. ■ Case 7. Let n = 2, and t = 3, (1):[M M 0 0 0] [M M 0 0 0]. . typeⅠ. So [M M 0 0 0] has cycle convergence.. 19. er. io. And then, [M x M 0 0] has cycle convergence, too.. sit. Since 0 < M－x < M, by case 5 (3), [M－x M－x M 0 M] has cycle convergence.. i Un. v.

(24) (2):[M 0 M 0 0] [M 0 M 0 0]. . typeⅡ. So [M 0 M 0 0] has cycle convergence.. 立. ■ Case 8.. ‧. ‧ 國. (1):[M M M 0 x]. 學. Let n = 3, and t = 1,. 政治大. [M M M 0 x]  [0 0 M x M－x]. y. Nat. n. al. Ch. engchi. er. io. And then, [M M M 0 x] has cycle convergence, too.. sit. Since 0 < M－x < M, by case 2 (1), [0 0 M x M－x] has cycle convergence.. i Un. v. (2):[M M 0 M x] [M M 0 M x]  [0 M M M－x M－x] Since 0 < M－x < M, by case 5 (1), [0 M M M－x M－x] has cycle convergence. And then, [M M 0 M x] has cycle convergence, too.. 20.

(25) ■ Case 9. Let n = 3, and t = 2, (1):[M M M 0 0]. . [M M M 0 0]  [0 0 M 0 M]. typeⅡ. So [M M M 0 0] has cycle convergence.. 立. [M M 0 M 0]= [M 0 M M M]. . ‧. ‧ 國. 學. (2):[M M 0 M 0]. 政治大. typeⅢ. y. Nat. n. er. io. al. sit. So [M M 0 M 0] has cycle convergence.. Ch. engchi. ■ Case 10. Let n = 4, and t = 1, (1): [M M M M 0] [M M M M 0] = [M 0 M M M]  typeⅢ So [M M M M 0] has cycle convergence.. 21. i Un. v.

(26) Since all the pentagons have cycle convergences with the largest value of a, b, c, d, e is equal M, by strong induction, all the pentagons must have cycle convergences if all the elements of pentagons are nonnegative integers and not all equal.. 立. 政治大. ‧. ‧ 國. 學. n. er. io. sit. y. Nat. al. Ch. engchi. 22. i Un. v.

(27) Chapter 4. Conclusion and Promotion. In our study, we find all the Diffy pentagons must have the following features if their elements are all nonnegative integers and not all equal: 1. All the Diffy pentagons must have cycle convergences. 2. All the cycle convergences must have the same type as the following figure for some integer n:. 立. 政治大. ‧ 國. 學 er. io. sit. y. Nat. [0 0 0 0 0]. ‧. 3. If all the values of vertices of pentagon are equal, this Diffy pentagon must converges to. al. Next, if we take [a b c d e] to be a cycle order pentagon and assume at least one element of a, b, c, d,. n. iv n C e is negative, we can subjoin one value which the absolute of the min{ a, b, c, d, e }. h eequal ngchi U. Then the. new pentagon must be isomorphic to the first pentagon. Also, if at least one element is rational, we can multiply each element by the least common multiple of denomicators such that all numbers of this pentagon become integers, then we can use the method above such that all numbers of this pentagon become nonnegative integers. By these two ways, we can easily promote our conclusion to rational number. During our study, we still find there are some rules of cycle convergences with hexagon, heptagon, and so on.. I hope this article can help us to continue to study Diffy pentagon even further.. 23.

(28) Appendix Strong induction The principle of mathematical induction asserts that P(k) being true implies P(k+1) is true, but sometimes is not enough.. Strong induction is a variant on proof by induction.. It comprises of the. following steps: 1. Set up a statement P(n), n  N 2. Confirm n=1 is true. 3. Assume P(1), P(2), P(3), ……, P(k) are true. 4. Show P(k+1) is true.. 立. 政治大. And then, we can say P(n) is true for all n  N.. ‧ 國. 學. Example 1 Let P(n) be n is the product of primes, where n is integer and n＞1.. ‧ sit. n. al. er. io. It is easy to check P(2) is ok.. y. Nat. Proof:. Assume P(2), P(3), P(4), ……, P(k) are true.. Ch. engchi. i Un. v. Then we just need prove k+1 is the product of primes. First, if k+1 is a prime: Then P(k+1) = (k+1), it means P(k+1) is true. Second, if k+1 is not a prime:. Then there must has some i and j  N, such that k+1 = i × j ,where 1＜ i, j＜ k. Since P(i), P(j) are true for all 1＜ i, j＜ k, we have P(k+1)=P(i) × P(j) is also true and the proof is completed.. 24.

(29) －1. Example 2 Every positive integer n can be expressed as n = ar2r + ar－12r. + … + a222 + a12 + a0,. where ai is 0 or 1 and r is some nonegative integer.. Proof: For n =1 : Let a0 =1, ok. Assume n is ok for all 1 ≦ n ≦ k－1. We just need to show n = k is ok, too. Let n = k be even:. Let. k k is an integer and ≦ k－1 2 2. 立. 政治大. k = ar2r + ar－12r－1 + … + a222 + a12 + a0 2. 學. ‧ 國. Then. Then n = k = ar2r+1 + ar－12r + … + a223 + a122 + a02 Let n = k be odd:. k 1 k 1 is an integer and ≦ k－1 2 2. n. al. sit er. io. k 1 = ar2r + ar－12r－1 + … + a222 + a12 + a0 2. y. Nat. Let. ‧. Then. v. Then n = k = ar2r+1 + ar－12r + … + a223 + a122 + a02 + 1 and the proof is complete.. Ch. engchi. 25. i Un.

(30) References [1] A. Behn, C. Kribs-Zaleta, and V. Ponomarenko, The Convergence of Difference Boxes. American Math. Monthly, volume 112, 426-438, (1995) [2] F. Breuer, Ducci Sequences in Higher Dimensions. Electronic Journal of Combinatorial Number Theory 7, #A24, (2007) [3] R. Brown and J. Merzel, The Length of Ducci’s Four-Number Game. Rocky Mountain Journal of Mathematics, volume37, 45-65, (2007) [4] N. Calkin, J. Stevens, and D. Thomas, A Characterization for the Length of Cycles of the N-Number Ducci Game. Fibonacci Quarterly, volume 43, no1, 53-59, (2005). [5] J. Creely, The Length of a Three-Number Game. Fibonacci Quarterly, volume 26, no2, 141-143, (1988). [6] A. Ehrlich, Periods in Ducci’s n-Number Game of Differences. Fibonacci Quarterly, volume 28,. 立. 政治大. ‧. ‧ 國. 學. no4, 302-305, (1990) [7] A. Ludington-Young, Ducci-Processes of 5-Tuples. Fibonacci Quarterly, volume 36, no5, 419-434, (May 1998) [8] A. Ludington-Young, Length of the 7-Number Game. Fibonacci Quarterly, volume 26, no3,195-204, (1998). [9] A. Ludington-Young, Length of the n-Number Game. Fibonacci Quarterly, volume 28, no3, 259-265, (1990).. y. Nat. sit. n. al. er. io. [10] W. Webb, The Length of the Four-Number Game. Fibonacci Quarterly, volume 20, no1, 33-35, (1982). [11] F.B. Wong, Ducci Processes. Fibonacci Quarterly, volume 20, no2, 97-105, (1982). [12] 蔡秀芬, Diffy Box (狄菲方塊). National Chengchi University, (2008). Ch. engchi. 26. i Un. v.

(31)