CHINESE JOURNAL OF PHYSICS VOL. 36, NO. 5 OCTOBER 1998 *
A Note on the Particle-Wave Correspondence
Yih-Yuh Chen
Physics Department, National Taiwan University, Taipei, Taiwan 106, R.O.C. (Received May 6, 1998)
We present an elementary argument showing how the Einstein relation E = hw and the de Broglie relation p = hk might come out naturally in the consideration of particle-wave correspondence.
PACS. 01.55.+b - General physics PACS. 03.75.-b - Matter waves.
While deeply awed by the famous Einstein relation
E = hw (1)
relating the energy with the (angular) frequency of the associated particle’s matter wave and the de Broglie relation
p = hk,
(2)
which assigns a wavenumber k to the same particle having a momentum p, the beginning students of quantum physics usually are also puzzled by how de Broglie ever came up with formulas as elegant as these. Though the origin of these two relations definitely called for the great insight of a genius, it also seems appropriate that one should not just leave the students with the impression that a better understanding of these two relations cannot be achieved (with hindsight, most probably) using a more elementary means. In fact, a couple of authors have already pointed out several interesting accounts on the “derivation” of these relations and their implications. For instance, Haslett [l] had translated part of de Broglie’s thesis to show how he originally conceived of the idea, and MacKinnon [2], Schlegel [3], Paul [4], Espinosa [5], and Brown and Martins [6] each had critically re-examined some aspects of de Broglie’s conceptions, while Motz [7] and Crawford [8] considered how an examination of the Doppler shift could naturally lead one to Eq. 1, and Silvert [9] showed that Eq. 1 can be guessed at from the same transformation property of the 4-vectors (w, 5) and (E,pT.
The purpose of this brief note is to introduce yet another motivation for both formulas by considering how one usually reconciles the concept of waves and the corpuscular picture in one theory. While none of the results presented below are new, it appears that, for one reason or another, ideas following the same line of reasoning shown here are not included in any of the relatively few textbooks on quantum physics available to the present author [lo] except one [ll].
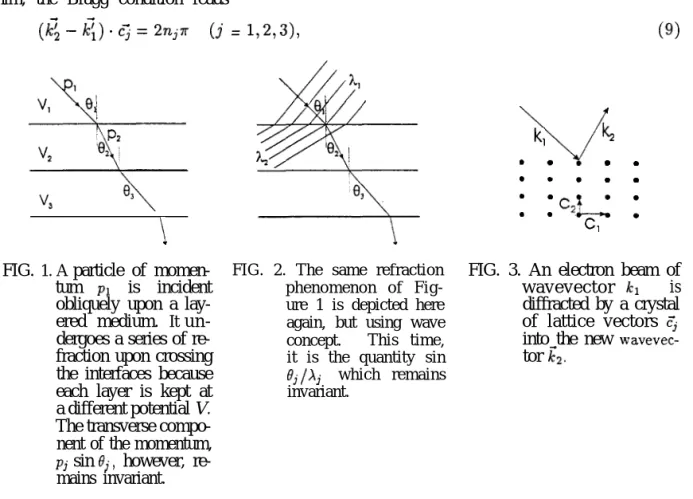
To begin with, let’s consider the classical particle of Figure 1 incident obliquely on a layered medium. The particle will bend at any of the interfaces in the medium because each layer is at a different potential V. (This is how one attempts to explain the phenomenon of refraction using the corpuscular picture.) Though the particle undergoes a series of 655 @ 1998 THE PHYSICAL SOCIETY OF THE REPUBLIC OF CHINA
656 A NOTE ON THE PARTICLE-WAVE CORRESPONDENCE VOL. 36
refractions on the course, two quantities remain invariant: its total energy E and the transverse momentum p sin 9. (Note that the latter is the mechanical explanation of Snell’s law sin 19r/ sin 02 = ps/pr =constant when we have only two layers.) On the other hand, if we consider the refraction of the wave of Figure 2, then the two invariant quantities are the frequency w and sin 0/X cx k sin 0, where X and k are the wavelength and the wavenumber, respectively. (Again, the latter is simply Snell’s law in the wave theory.)
If we believe that a particle is associated with a wave, then the two views presented above had better agree if we are to have a self-consistent theory. This suggests that w should be a function of the energy E alone, and that p/k should be a constant independent of which layer the particle is in. Thus, our starting relations are
w = w(E), (3)
P=
rlk,
(4)
where 77 is some constant independent of V. Eq. 4 is reminiscent of the famous de Broglie relation p = lik (Eq. 2) except that at this stage we have no way of telling whether 77 is a universal constant or if it might depend on some of the intrinsic properties such as mass or charge of the particle, or worse, if it might depend on the total energy E of the particle.
Now we look at the situation more closely. The wavenumber k clearly is a function of the potential V, because it assumes a different value in each layer. We will denote it by k = k(V). Also, there is a dispersion relation characterizing how w varies with k when the wave is moving inside a specific layer. This dispersion relation might assume a slightly different form when the wave is moving in a layer of different potential V. In other words, we should express the dispersion relation as w = w(k, V). Then the reason why w doesn’t actually depend on which layer the wave is travelling in (or, equivalently, the potential V ) is simply because the functional form of k(V) is such that w(k(V),V) does not have any V-dependence. The same goes with the energy E = E(V,p) = E(V, qk) = E(V, qk(V)).
But we recall that a plane wave is not something we should identify our classical particle with, because it has an infinite spatial extent. Rather, we should consider a wave packet which is more or less localized in space. The speed the wave packet has in a medium is the group speed
v = dw(k, V)
dk
-It is this speed which should be most reasonably identified with the particle speed. Noticing that w = w(E) = w(E(V,p)) and that p = yk we immediately have
dW
dw BE
dw
~E(I/,P)~‘=?%=dE
dk =dE dp ’An example will illustrate what this equation actually tells us. Suppose we have
n
E=V+&
and v = p/m, then Eq. 5 yields
dE -=
dw 77
(5)
(6)
VOL. 36 YIH-YUH CHEN 657
E = VW (7)
if we assume that the constant 77 in Eq. 4 is a universal constant. Similarly, if we take
E = V + dp2c2 •t m2c4
for a relativistic particle and forget about the issue of covariance, then simple algebra shows that we will still recover Eq. 6.
In fact, our ability in deriving Eq. 6 is not in any way related to the specific form of
E(V,p). Using Hamilton’s equation of motion
dq dH(q,p) = dE(JW
z= ap 8P
for the position variable q and identify dq/dt with the particle velocity V, we see that Eq. 6 is a direct consequence of Eq. 5.
The remaining question is, therefore, why is it that 7 does not depend on the to-tal energy E at the very least ? To answer this question, we may consider the following Davisson-Germer type experiment (Figure 3). In this experiment we may view the inci-dent beam of electrons as matter waves which are diffracted by the lattice scatterers. Only diffracted directions which satisfy the Bragg condition
.
-(Ic2 - ki) . C? = 27lj7T (j = ~2~3) (8)
for some integers nj will exhibit a strong peak in intensity and be measurable. Here, & and <r are the diffracted and incident wavevectors of the electron matter wave, respectively, and the c:‘s are the three lattice vectors for the specific crystal. But what does this experiment appear to someone else moving at a velocity ?i relative to us, the laboratory observers? To him, the Bragg condition reads
(Ic: - k:) * CT = 2?lj7T (j = I,2,3), (9)
\ FIG. 1. A particle of
momen-tum pi is incident obliquely upon a lay-ered medium. It u n -dergoes a series of re-fraction upon crossing the interfaces because each layer is kept at a different potential V. The transverse compo-nent of the momentum, pj sin Sj, however, re-mains invariant.
FIG. 2. The same refraction phenomenon of Fig-ure 1 is depicted here again, but using wave concept. This time, it is the quantity sin ej lxj which remains invariant.
\/’
4
kz
. .
. .
. . . . .
. .
. . ClK :
ClFIG. 3. An electron beam of wavevector ICI is diffracted by a crystal of lattice vectors ?j into the new wavevec-tor $2;.
658 A NOTE ON THE PARTICLE-WAVE CORRESPONDENCE VOL. 36
because the electron wavevectors Icf and Gr certainly appear different from I& and & to him. (To avoid complications, we have assumed that the speed jjZl[ is much smaller than the speed of light so that Galilean transformation suffices in our discussion.)
Now, if we have a quasi-de Broglie relation such as p” rl(W,
then Eq. 8 will become
&p -
P-i)
.cT = 271~~ (j = 1,2,3) (10) because the electron has the same energy E before and after the diffraction, whereas Eq. 9 --will instead read(
7 7
P, 4% - rl(EI)
- C; = 2nja (j = 1,2,3).
(Please notice that to the moving observer the diffracted electron usually has an different from its incident value I$.) In view of 3 = p’- rnZ we may recast Eq.
1 1 - - -6% 77(% >) * C: = 2njr (j = 1,2,3)
(11)
energy Ei 11 intoThis equation will coincide with Eq. 10 for any velocity Z if it so happens that q is not a function of the energy E. (For instance, we can try expanding 77 in the small velocity Z to argue that 77 should be a constant function.) Put differently, to have consistency, it is only reasonable if 7 depends at most on the intrinsic properties of the particle.
A c k n o w l e d g m e n t s
This work was supported by the Gou-Pee Papers Foundation. R e f e r e n c e s
J. W. Haslett, Am. J. Phys. 40, 1315-1320 (1972); J. W. Haslett, Am. J. Phys. 41, 445 (1973); J. W. Haslett, Am. J. Phys. 60, 583 (1992); J. A. Henry, Am. J. Phys. 60, 1065 (1992).
E. MacKinnon, Am. J. Phys. 44, 1047-1055 (1976).
R. Schlegel, Am. J. Phys. 45, 871-872 (1977); E. MacKinnon, Am. J. Phys. 45, 872-873 (1977).
D. Paul, Am. J. Phys. 48, 283-284 (1980); J. Haslett, Am. J. Phys. 49, 192 (1981). J. M. Espinosa, Am. J. Phys. 50, 357-362 (1982).
H. R. Brown and R. de A. Martins, Am. J. Phys. 52, 1130-1140 (1984). L. Motz, Am. J. Phys. 41, 1016-1017 (1973).
F. S. Crawford, Am. J. Phys. 50, 269-270 (1982). W. Silvert, Am. J. Phys. 42, 429-430 (1974).
Some references are: R. A. Serway, C. J. Moses, and C. A. Moyer, Modern Physics (Saunders College Publishing, 1997); J. J. Brehm and W. J. Mullin, Inlroduc2ion lo the Sirzlclure of Matter (Wiley, New York, 1989); S. Gasiorowicz, Quan2~m Physics (Wiley, New York, 1996); A. Beiser, Concepts of Modern Physics (McGraw-Hill, New York, 1995); R. Eisberg and R. Resnick, Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (Wiley, New York, 1974).
F. K. Richtmyer, E. H. Kennard, and T. Lauritsen, Introduction to Modern Physics (McGraw-Hill, New York, 1955), pp. 172-178.