Analysis of minimum zone sphericity error using minimum potential energy theory

(1)

Analysis of minimum zone sphericity error using minimum potential

energy theory

Kuang-Chao Fan

a,

*, Ji-Chun Lee

b

a_{Department of Mechanical Engineering, National Taiwan University, Taipei, Taiwan, Republic of China} b_{Department of Mechanical Engineering, National Chung-Hsing University, Taipei, Taiwan, Republic of China}

Received 28 October 1997; received in revised form 2 June 1998; accepted 28 August 1998

Abstract

Theoretical derivation of the minimum zone criteria of sphericity error based on the principle of minimum potential energy is proposed. All the measured data points are enclosed by two concentric spherical surfaces between which a fictitious spring is assumed to be placed. These two concentric spherical surfaces can be mathematically determined by five active data points. When the spring contracts, the potential energy of the simulated mechanical system tends to reduce which yields two new concentric spheres with smaller radial separation and new active data points. Finally, a stable state will be reached to the condition of minimum potential energy. The criteria conforming to such a state can be derived. A direct search scheme to the global minimum solution is also proposed. The clearance between such two concentric spherical surfaces is the minimum zone of spherical form error. © 1999 Elsevier Science Inc. All rights reserved.

Keywords: Sphericity error; Minimum zone method; Potential energy; Virtual work; Static equilibrium

1. Introduction

Sphericity is a kind of form error which is broadly used in industry for the geometrical measurement of precision balls. Any defects on the surface, such as surface roughness and form error, may result in the life reduction, wear, and run-out rotation. Therefore, effective and precise evaluation of the sphericity is an important issue.

There are various kinds of form errors, such as straight-ness, flatstraight-ness, roundstraight-ness, sphericity, and cylindricity. There are also many kinds of evaluation techniques. Cheraghi [1] formulated the straightness and flatness errors by nonlinear optimization problems with a linear objective function and nonlinear constraints. Wang [2] applied the theory of non-linear constrained optimization to evaluate straightness, flatness, roundness, and cylindricity. Kanada [3] computed the minimum zone sphericity using iterative least squares and the downhill simplex methods. Carr [4,5] proposed minimum zone searching algorithms that solved a sequence of linear problems and converged to the solution of the nonlinear one. Huang [6,7] evaluated the minimum zone

straightness and flatness form error based on the control line, or control plane, rotation scheme (CLRS or CPRS) which could result in the exact solutions. In this article, we have not only derived some lemmas for finding the criteria of minimum zone sphericity error, but also proposed a fast computational algorithm, starting from the least squares result, which can direct search to the minimum zone state.

2. Mechanical model of minimum zone spherical form error

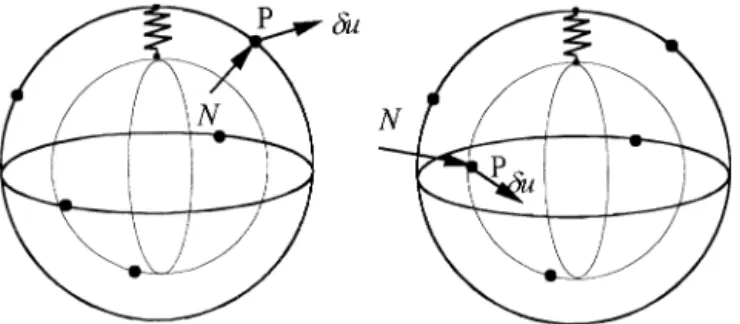
A simulated mechanical system is used to model the problem of minimum zone spherical form error. A group of supports are fixed at positions of measured data points and enclosed by two fictitious concentric semi-rigid spherical surfaces. These supports are assumed to withstand compres-sion only. The concentric semi-rigid spherical surfaces should observe the law that they remain concentric and spherical when deformed. A fictitious spring is assumed to be placed between them, as shown in Fig. 1, and is the only component of the mechanical system that can store the elastic energy.

From the geometrical point of view, the degree of free-dom of the system is five and there are five active supports * Corresponding author. Tel.:1886-2-2362-0032; fax:

1886-2-2364-1186.

E-mail address: fan@ccms.ntu.edu.tw (K.-C. Fan)

(2)

at the same time. These five active supports are located at the corresponding five measured points which are contacted by the enclosing spherical surfaces. In other words, at least five points must be in contact with the two enclosing con-centric spherical surfaces. When the spring contracts, these active supports will be replaced by new contact points and the elastic energy of the system will tend to reduce. Finally, it will reach a stable state of minimum potential energy. The problem of the minimum zone spherical form error is then transformed into the problem of minimum potential energy of the simulated mechanical system. It can be stated as: Minimizing the elastic potential energy

U51

2ku

2 ₍₁₎

subjected to all supports (measured data points) enclosed by the two concentric spherical surfaces. In Eq. (1), k is the spring constant of the fictitious spring and u is its displacement.

3. Formulation of system equations

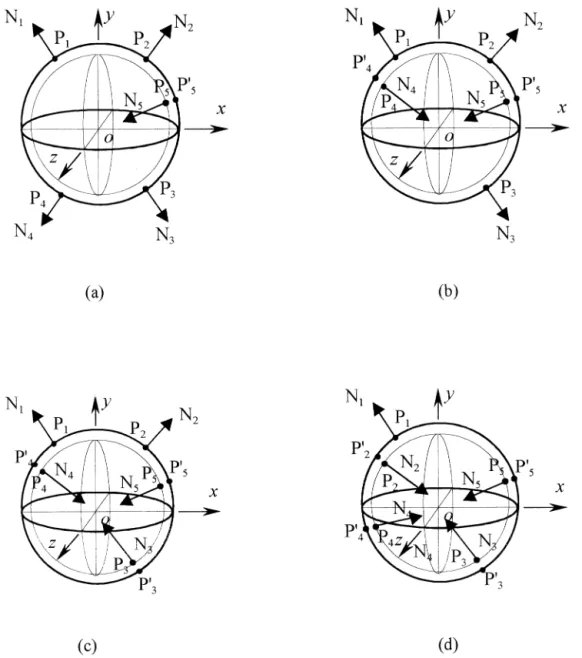
From the geometrical point of view, there are four modes of concentric spherical surfaces: (1) Mode M4-1, four data points on the outer sphere and the last data point on the inner sphere; (2) mode M3-2, three data points on the outer sphere and the other two data points on the inner sphere; (3) mode M2-3, two data points on the outer sphere and the other three data points on the inner sphere; (4) Mode M1-4, one data point on the outer sphere and the other four data points on the inner sphere. Assume the current active data points are P1to P5and the active supports of the simulated mechanical system are placed at these five positions respec-tively. When these supports are released the free body diagrams are shown in Fig. 2 in which reactions on the active supports of P1to P5are N1to N5respectively, and Pi

is the corresponding point on the outer surface when Piis on

the inner surface. Without the loss of generality, let the

center of the concentric sphere be the origin of the coordi-nate system, the outer sphere be the unit sphere (radius

Ro51), and the radius of the inner sphere be Ri(Ri5 Ro/a

5 1/a,a . 1). Let the coordinates of these active data points

be P1(x1,y1,z1), P2(x2,y2,z2), P3(x3,y3,z3), P4(x4,y4,z4) and

P5(x5,y5,z5). For mode M4-1 the equilibrium equations of reactions are:

O

Fx5 0 N1x11 N2x21 N3x31 N4x42 N5ax55 0 (2)

O

Fy5 0 N1y11 N2y21 N3y31 N4y42 N5ay55 0 (3)

O

Fz5 0 N1z11 N2z21 N3z31 N4z42 N5az55 0 (4) where(Fx5 0, (Fy5 0, (Fz 5 0 mean the sum of the

x ,y, and z components of all reactions should equal to zero at equilibrium condition.

Let [Eq. (5)]

P955 ~x95, y95, z95! 5a~x5, y5, z5! (5)

The corresponding data point P95(x95,y95,z95) with respect to

P5is on the outer unit sphere (shown in Fig. 2a). Assume the center of these two concentric spheres and the inner spherical surface are fixed and the outer spherical surface is given an admissible virtual displacementdu. From the prin-ciple of virtual work, we have

N1du 1 N2du 1 N3du 1 N4du 5 d

S

1 2ku

2

D

_{5 kudu}

N11 N21 N31 N45 ku 5 C $ 0 (6)

Similarly, Let the center of these concentric spheres and the outer spherical surface be fixed and the inner spherical surface be given an admissible virtual displacementdu. We have

N5du 5 d

S

1 2ku

2

D

_{5 ku}_du

N55 ku 5 C $ 0 (7)

Combining Eq.(2) to (4) and (6), (7), the system equations of mode M4-1 can be represented in matrix form as [Eq. (8)]

3

x1 x2 x3 x4 2 x95 y1 y2 y3 y4 2 y95 z1 z2 z3 z4 2 z95 1 1 1 1 0 0 0 0 0 1

45

N1 N2 N3 N4 N5

6

5

0 0 0 C C

6

(8)

Similarly, from equilibrium equations and the principle of virtual work we have the system equations of mode M3-2 as [Eq. (9)]

(3)

3

x1 x2 x3 2 x94 2 x95 y1 y2 y3 2 y94 2 y95 z1 z2 z3 2 z94 2 z95 1 1 1 0 0 0 0 0 1 1

45

N1 N2 N3 N4 N5

6

5

0 0 0 C C

6

(9)

The system equations of mode M2-3 are [Eq. (10)]

3

x1 x2 2 x93 2 x94 2 x95 y1 y2 2 y93 2 y94 2 y95 z1 z2 2 z93 2 z94 2 z95 1 1 0 0 0 0 0 1 1 1

45

N1 N2 N3 N4 N5

6

5

0 0 0 C C

6

(10)

The system equations of mode M1-4 are [Eq. (11)]

3

x1 2 x92 2 x93 2 x94 2 x95 y1 2 y92 2 y93 2 y94 2 y95 z1 2 z92 2 z93 2 z94 2 z95 1 0 0 0 0 0 1 1 1 1

45

N1 N2 N3 N4 N5

6

5

0 0 0 C C

6

(11)

Solving the system equations for each mode, we obtain the corresponding reactions on each support for each mode.

4. Theorem of minimum zone spherical form error

In a stable state, the reactions at all active supports must be compression. If the reactions are tension then the spherical Fig. 2. Free body diagrams of four modes of concentric spherical surfaces: a) Mode M4-1, b) Mode M3-2, c) Mode M2-3, d) Mode M1-4.

(4)

surface and the support will separate and the system will not be stable. In this article, the sign convention of the reaction is positive for compression, and negative for tension. In other words, for reactions that act on the outer spherical surface with direction outward are positive and reactions that act on the inner spherical surface with direction inward are positive. It can be shown that when all the active reactions are positive (i.e., compression), the simulated mechanical system is in a stable state and has minimum elastic potential energy.

Lemma 1: The simulated mechanical system is in a

stable state if all reactions at active supports are positive.

Proof:

Let the support at data point P on the concentric spherical surfaces be released and replaced by the reaction N (shown in Fig. 3) and all other supports remain unchanged.

By Castigliano’s first theorem [8] we have [Eq. (12)]

dU 5 NY z duY . 0 (12)

wheredU is the change of potential energy of the system due to the displacementdu of the outer spherical surface at

P. For a stable system, the change of potential energy of the

system must be positive.

Because all supports must be enclosed by the two concentric spherical surfaces. The direction of admissible displacement duY must be outward if the released active support is located at the outer spherical surface, and inward if it is located at the inner spherical surface. From Eq. (12), we can also conclude that reaction N and dis-placementdu must have the same direction (i.e., reaction

N is positive). According to the above discussion, we

reach the conclusion that when all reactions are positive (compression), any further deformation of the two con-centric spherical surfaces will lead to the increase of elastic potential energy of the system. In other words, if all reactions are positive the system is then in a stable state.

Lemma 2: Mode M4-1 and M1-4 are unstable. Proof:

Let C5 1 for convenience, then the system equations of mode M4-1 are [Eq. (13)]

3

x1 x2 x3 x4 2 x95 y1 y2 y3 y4 2 y95 z1 z2 z3 z4 2 z95 1 1 1 1 0 0 0 0 0 1

45

N1 N2 N3 N4 N5

6

5

0 0 0 1 1

6

(13)

From Equation (13), we have N551, and this equation can be simplified to [Eq. (14)]

3

x1 x2 x3 x4 y1 y2 y3 y4 z1 z2 z3 z4 1 1 1 1

45

N1 N2 N3 N4

6

5

x95 y95 z95 1

6

(14) Let D5

3

x1 x2 x3 x4 y1 y2 y3 y4 z1 z2 z3 z4 1 1 1 1

4

D15

3

x95 x2 x3 x4 y95 y2 y3 y4 z95 z2 z3 z4 1 1 1 1

4

(15)

Expressing in vector form, Equation (15) becomes [Eq. (16)]

D5 rY14z nY234 and D15 rY54 z nY234 (16) where r Yi5 ~xi, yi, zi! or ~x9i, y9i, z9i! r Yij5 rYi2 rYj nY2345 rY243 rY34

and the last term of above refer to the normal of the plane formed by points P2, P3, and P4. From the Cramer’s rule, we have [Eq. (17)] N15 D1 D 5 r Y54z nY234 r Y14z nY234 (17) Fig. 3. Free body diagram with one active support released.

(5)

From Equation (17), we conclude that the sufficient and necessary condition for N1. 0 is [Eq. (18)]

r

Y14z nY234. 0 and rY54z nY234. 0

or rY14z nY234, 0 and rY54z nY234, 0 (18)

This implies that P1and P95should be on the same side of the plane formed by P2,P3,P4(shown in Fig. 4). Similarly, we can also conclude that [Equations (19), (20), (21)]

r Y24z nY314. 0, rY54z nY314. or rY24z nY314, 0, r Y54z nY314, 0 (19) r Y34z nY124. 0, rY54z nY124. or rY34z nY124, 0, r Y54z nY124, 0 (20) r Y41z nY321. 0, rY51z nY321. or rY41z nY321, 0, r Y51z nY321, 0 (21)

According to the above relations, the necessary and sufficient condition for N2. 0 is that P2and P95should be on the same side of the plane formed by P1,P3,P4; for

N3.0, P3and P95should be on the same side of the plane

formed by P1,P2,P4; and for N4.0, P4and P95should be on the same side of the plane formed by P1,P2,P3. We then have the following conclusion: the necessary and sufficient condition for all reactions to be positive (com-pression) is that the point P95should be located inside the tetrahedron formed by P1,P2,P3,P4. However, since P1,P2,P3,P4,P95are all on the same unit sphere, the con-clusion made above is impossible. In other words, Modes M4-1 is unstable. This situation can also be applied to mode M1-4.

Lemma 3: Mode M3-2 is stable if and only if P94and P95 are on the opposite sides of the plane formed by P1,P2,P3 and the line segment P94P95 intersects the triangle

DP1,P2,P3; Mode M2-3 is stable if and only if P1and P2are on the opposite sides of the plane formed by P93,P94,P95and the line segment P1P2 intersects the triangle formed by

DP93,P94,P95.

Proof:

Let C51, then the system equations of mode M3-2 are

3

x1 x2 x3 2 x94 2 x95 y1 y2 y3 2 y94 2 y95 z1 z2 z3 2 z94 2 z95 1 1 1 0 0 0 0 0 1 1

45

N1 N2 N3 N4 N5

6

5

0 0 0 1 1

6

(22) We have N41 N55 1 N55 1 2 N4 (23)

Substituting Equation (23) into Equation (22) yields: [Eq. (24)]

3

x1 x2 x3 x952 x94 y1 y2 y3 y952 y94 z1 z2 z3 z952 z94 1 1 1 0

45

N1 N2 N3 N4

6

5

x95 y95 z95 1

6

(24) Let [Eq. (25)] D5

3

4

, D15

3

4

, D25

3

4

D35

3

4

, D45

3

x1 x2 x3 x95 y1 y2 y3 y95 z1 z2 z3 z95 1 1 1 1

4

(25) Expressing in vector form, Equations (25) become [Eq. (26)] D5 2rY54z nY231 D15 2rY54z nY235 D25 2rY54z nY315 D35 2rY54z nY125 D45 2rY51z nY231 (26) where r Yi5 ~xi, yi, zi! or ~x9i, y9i, z9i! r Yij5 rYi2 rYj

rnijk5 rYik3 rYjk5 ~rY 2 rYk)3 ~rYj2 rYk)

From the Cramer’s rule, we have [Equations (27), (28), (29), (30)]

(6)

N15 D1 D 5 r Y54z nY235 r Y54z nY231 , N25 D2 D 5 r Y54z nY315 r Y54z nY231 N35 D3 D 5 r Y54z nY125 r Y54z nY231 , N45 D4 D 5 r Y51z nY231 r Yl54z nY231 (27) Case I: When rY54 z nY231 . 0 N1. 0 if and only if rY54z nY235. 0 (28) N2. 0 if and only if rY54z nY315. 0 (29) N3. 0 if and only if rY54z nY125. 0 (30) N4. 0 if and only if rY51z nY231. 0 (31)

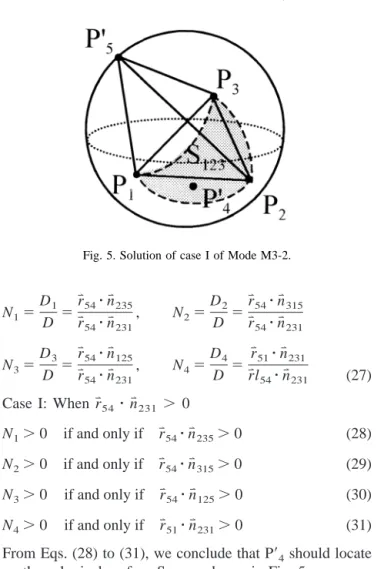
From Eqs. (28) to (31), we conclude that P94should locate on the spherical surface S123as shown in Fig. 5.

Hence,

r

Y54z nY231. rY51z nY231. 0 1. N4. 0

From Equation (23), we have [Equations (32), (33), (34), (35)]

N55 1 2 N4. 0

Case II. When rY54z nY231 , 0

N1. 0 if and only if rY54z nY235, 0 (32)

In this case, the solution that satisfies Eqs. (32) to (35) does not exist.

From the above discussions, we can see that mode M3-2 is stable, and all reactions are positive if and only if P94and P95 are on the opposite sides of the plane formed by P1,P2,P3,and the line segment P94P95intersects the triangle

DP1P2P3. Similarly, mode M2-3 is stable if and only if P1 and P2 are on the opposite sides of the plane formed by P93,P94,P95and the line segment P1P2intersects the triangle

DP93P94P95. These are the criteria for the minimum zone condition of sphericity error.

5. Computational algorithm

Let’s call those five data points that determine the con-centric spheres are active data points contained in the set S. From Lemma 1, we know that the reactions act on the active points should be positive. If any of these reactions is neg-ative, it means that the potential energy can be further reduced. In the other words, the data point of negative reaction can be removed from the set S and new searched data point should be added in such that they can form two new concentric spheres having less potential energy. In general, there may be more than one negative reaction in the beginning of the search process. In this computational al-gorithm, we only exchange one active point each time and the data point which has the most negative reaction is chosen to be removed from S. This state is called the Fig. 5. Solution of case I of Mode M3-2.

(7)

transition mode. In the transition mode, we need to search one more new data point to form concentric spheres having less potential energy, by the use of the proposed search scheme as described below.

The algorithm for finding the minimum zone sphericity is as follows.

1. Compute the least squares solution of sphericity er-ror, and find the outer and inner enclosing spherical surfaces Co, Ci and the corresponding active data points Poand Pi.

2. Randomly generate two virtual data points on the inner surface Cito form a temporary transition mode T1-3.

3. Compute the plane equation and its normal vector formed by those three inner active points.

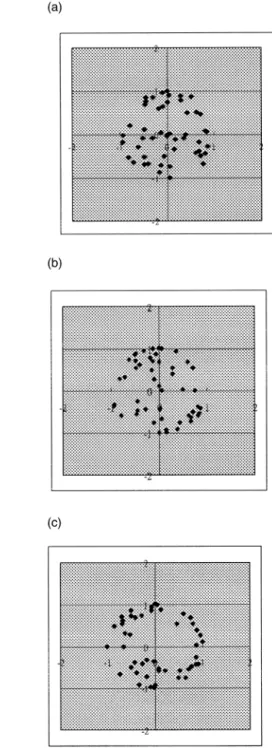
4. Gradually move the current sphere center along the above mentioned normal direction, up or down, as Fig. 7. Distribution of data points of Table 1 on the a) X-Y plane, b) X-Z plane, c) Y-Z plane.

Table 1

Sphericity data set and its result (unit: mm) No. X Y Z 1 0.81814 20.43615 20.38525 2 20.80885 20.53045 0.27905 3 0.03749 0.90643 20.42737 4 0.86935 20.27403 20.42518 5 20.50786 20.07441 0.86060 6 0.75348 20.67012 20.00610 7 0.05867 21.00773 20.00198 8 20.17486 0.60442 0.78297 9 0.71121 20.50123 20.50042 10 20.47493 20.51466 0.71992 11 0.06016 20.74129 20.67432 12 0.05337 0.02006 1.00515 13 0.29869 0.87920 0.38988 14 20.15488 20.86697 0.48585 15 0.38994 20.00060 20.92592 16 0.00776 0.73922 0.68741 17 0.62090 0.52006 20.59341 18 0.00952 20.03493 21.00376 19 20.44592 0.76584 20.47827 20 0.01069 0.99511 0.11265 21 20.93371 20.17351 20.33160 22 20.48121 20.69836 0.53717 23 0.50394 0.86933 0.03322 24 0.80924 0.07332 20.59398 25 0.84569 0.06876 20.53570 26 0.36179 20.07902 0.93410 27 20.78624 0.20326 20.59063 28 20.46529 0.69616 20.55167 29 20.93402 20.02267 20.35813 30 0.43016 0.49319 20.76122 31 20.46929 0.11501 0.88119 32 0.60788 20.41130 0.68580 33 0.70712 0.46598 0.53998 34 0.67398 20.38068 20.63956 35 20.06245 20.50544 0.86696 36 20.09577 0.96216 0.26433 37 0.29318 0.79379 0.54237 38 20.39873 20.68009 0.61867 39 20.30833 20.07805 0.94937 40 20.70424 20.64359 0.31476 41 0.67010 20.17187 20.72841 42 20.12359 20.70688 0.70559 43 20.09694 0.64820 20.75729 44 20.13014 0.04876 0.99815 45 20.28485 0.86262 20.43728 46 0.16745 20.11142 20.98603 47 0.00946 20.00746 1.00873 48 0.15374 20.33634 20.93141 49 20.44828 0.85926 20.25853 50 20.61673 20.28843 0.73859

Minimum zone error 7.660mm

(8)

shown in Fig. 6a, until the first new point is con-tacted by the new concentric spheres determined by this point and original four active points, forming mode M2-3 or M1-4.

5. Compute the reactions of these five active points with Eq. (10) for mode M2-3, or Eq. (11) for mode M1-4, and discard one virtual point which has the most negative reaction, forming mode T1-3 or T2-2. 6. If the current mode is T1-3, repeat Steps 3 to 5 to

discard the remaining virtual point.

7. If the current mode is T2-2, generate a new search line which is the intersection of two planes perpen-dicular to the inner line (P1P2) and the outer line (P3P4) respectively, as shown in Fig. 6b. A new active point will be found together with a new mode. 8. Compute the five reactions and discard the active point having the most negative reaction, and search a new point with current mode, T2-2, or T1-3, or T3-1 (similar to T1-3).

9. Repeat Step 8 until all reactions are positive. 10. The final mode must be M2-3 or M3-2, and the

radial separation of the concentric spheres is the minimum zone solution.

It should be noticed here that the search scheme of this algorithm starts from the result of the least squares solution which is already very close to the minimum zone solution. The criterion of the minimum zone solution has been proven by the three Lemmas in this paper. In addition, from the geometrical point of view, we will never find two groups of concentric spheres in space both conforming to the minimum zone crite-rion. Therefore, the proposed algorithm can be guaranteed as the global minimum zone solution.

6. Example

An example shown in Table 1 is illustrated to demonstrate the criterion proposed in this research. Data points are gener-ated randomly such that they are all locgener-ated between two concentric spherical surfaces of radii equal to 0.995 and 1.005, respectively. The distribution of data points are shown in Fig. 7 with different projection views. The result is compared with the least squares method and verified by comparing the actual spherical form error. The actual spherical form error is found by the exhausting search that examined all the possible com-binations. After examining all the possible combinations for data set in Table 1, we found that the solution is the same as that in our approach. The minimum zone sphericity error is

7.66mm dominated by the mode M3-2 with data points 7, 16,

and 45 on the outer spherical surface and 20, 39 on the inner one. With the use of the proposed direct search scheme we need totally only five or six iterations to get the required solution. The computer time for this example is only 1.3 seconds with a PC/486, DX-266.

7. Conclusions

An approach with minimum potential energy analogy to the minimum zone solution of spherical form error is pro-posed in this research. The problem of finding the minimum zone sphericity error is transformed into the problem of finding the minimum elastic potential energy of the corre-sponding mechanical system. The minimum zone solution can be justified by the proposed comprehensive criteria.

In this report, we have derived three lemmas to prove the sufficient and necessary condition of the minimum zone criteria. They could be implemented to solve the problem of minimum zone sphericity error easily. A computer program is developed which provides direct and rapid search algo-rithm. This concept can also be extended to solve other minimum zone form error problems. Actually, it is a unified approach for finding minimum zone form errors, such as straightness, flatness, roundness, sphericity, cylindricity, etc. A series of reports in this respect will be forthcoming.

References

[1] Cheraghi SH, Lim HS, Motavalli S. Straightness and flatness tolerance evaluation: an optimization approach. Precision Engineering 1996; 18(1):30 –7.

[2] Wang Y. Minimum zone evaluation of form tolerances. Manufacturing Review 1992;5(3):213–20.

[3] Kanada T. Evaluation of spherical form errors: computation of spher-ical form error by means of minimum zone method and some exam-inations with using simulated data. Precision Engineering 1995;17(4): 281–9.

[4] Carr K, Ferreira P. Verification of form error tolerances Part I: basic issues, flatness, and straightness. Precision Engineering 1995;17(2): 131– 43.

[5] Carr K, Ferreira P. Verification of form error tolerances Part II: cylindricity and straightness of a median line. Precision Engineering 1995; 17(2):144 –56.

[6] Huang ST, Fan KC, Wu JH. A new minimum zone method for evaluating straightness errors. Precision Engineering 1993;15(3):158 – 65. [7] Huang ST, Fan KC, Wu JH. A new minimum zone method for evaluating flatness errors. Precision Engineering 1993;15(1):25–32. [8] Castigliano A. Theorie de l’equilibre des systemes ’elastiques et ses