高中學生的「失重」概念之研究

高中學生的「失重」概念之研究 71 物理教育學刊

2008, 第九卷第一期, 1-16

Chinese Physics Education 2008, 9(1), 1-16

物理教育學刊

2009, 第十卷第一期, 1-26

Chinese Physics Education 2009, 10(1), 1-26

高中學生的「失重」概念之研究

林明良

1 蘇明俊2 江新合1 1 國立高雄師範大學 科學教育研究所 1 樹德科技大學 休閒事業管理系 （投稿日期：民國 97 年 10 月 20 日，修訂日期：98 年 06 月 15 日，接受日期：98 年 07 月 14 日） 摘要：在懸吊鋼繩斷裂而自由落下的電梯中，站在磅秤上的人測得的重量為零，所以 說人處於「失重」狀態。如果根據一般教科書採用的「重量即物體所受重力」或「物 體所受重力的大小」來推論，如此一來，物體失重時其所受重力也是零。可是，失重 時真的沒有重力作用嗎？本研究旨在探討高中學生在失重教學後所建構的「失重」概 念。研究對象為學過力學的高二學生 96 人。研究方法以量化的調查研究為主，質性的 個案訪談為輔。研究工具為自編的「失重概念問卷」，以霍金體驗失重飛行的新聞為背 景，題目形式採用「事實—理由」兩階段設計，並在每階段另增加一層學生對自己作 答的「信心加權」評分，而形成兩階段四階層測驗。在「理由」階段，前測問卷為開 放式，後測則為是非題，並將信心加權改為逐題對其說服力評分(1 最低，5 最高，0 為「非」)。研究發現：約四成學生知道失重並不是失去重力而是感受不到重量，而同 時能正確說出失重飛行時，何時會產生失重狀態者，僅剩 8.5%。學生的失重概念心智 模式可歸納成七種：測量說、離心力說、漂浮說、高度說、大氣說、零重力說、及直 覺說。重量的重力定義可能導致失重即失去重力的錯誤推論，建議教師教學時應釐清 重量與重力的概念。 關鍵詞：另有概念、失重、重力、重量

壹、前言

「重量(weight)」的定義可以分為兩種 (Figueiredo, 2008; Galili & Lehavi, 2003)。一 種是越高年級的教科書越少採用的操作型定 義，例如：重量是「物體作用在其支撐或懸

吊物的力 (Marion & Hornyak, 1985)」；另一

種則是以重力來定義，例如：「物體所受地球

引力即物體重量」，並說明「地球引力又稱為

重 力 (gravitational force) 」 ( 例 如 Serway, 1996)。第一種定義的重量是接觸力；第二種 定義的重量就是重力，是超距力。

King(1962)指出，由於在討論「人在太 空」的議題時，「失重(weightlessness)」這個 名詞引發許多人的困惑，促使他去考慮「重 量」的定義，他主張重量是接觸力，有別於 「重力」，並建議基礎物理教科書的作者，應 該仔細區別這兩者。隨後的研究者(如 Taylor, 1974; Galili, 1993, 1995, 2001)也支持這個主 張，但是卻鮮有教科書作者接受(Figueiredo, 2008)。 我國國中及高中教科書，甚至國小自然 領域的能力指標也都採用第二種定義—「重 量即重力」來說明重量的來源，並且提出質 量 m 的物體，其重量 W=mg，其中 g 為重力 加速度。 這樣的定義容易導致對「失重狀態」這 個概念的誤解，因為失重若是指失去重量， 根據重量的重力定義，失重也指失去重力。 而教科書以「磅秤顯示的重量(即視重)」為 零來解釋「失重」，這樣的解釋可能引發另一 個問題：「重量」與「磅秤顯示的重量」有何 不同？答案又回到前述的定義，前者是重力 定義，是超距力，而後者是操作型定義，是 接觸力，顯然它們指不同的物理量，卻都用 了「重量」的說法。在這樣的教學背景下， 學生建構了怎樣的「失重」概念，就成了值 得探討的問題。 本研究的目的在探討高中學生學過重 力、重量及失重後，所建構的失重概念，以 作為教學的參考。

貳、文獻探討

重量概念發展起源於日常生活的直接經 驗，而重力概念的發展卻是來自於學校的概 念教學或科普書籍及媒體。直接的經驗使得 學生的重量概念遠比重力概念根深蒂固，因 此教科書以重力即重量來遷移學生的概念， 這樣的作法讓學生很快接受了重力概念，但 是同時也造成概念的混淆。以下將討論學生 的重量與重力概念之發展，以及教科書與科 普雜誌對重量與重力的定義。

一、學生的重量與重力概念之發展

學生所持有的日常物理現象概念，其發 展受三方面影響 (Osborne & Wittrock, 1985; Claxton, 1996)：一為個人的「直觀科學 (gut science)」，來自對該現象的直覺與自然的反 應，未經審慎思考與反思，常具有許多迷思 概 念 ； 二 為 社 會 的 「 世 俗 科 學 (lay science)」，源自日常的語言運用與媒體影 像 ； 三 為 正 式 學 術 的 「 學 校 科 學 (school science)」，是基於學校課堂的符號化、理想 化世界，卻常與直觀違背。學生的重量與重 力概念的發展也不例外，日常的經驗、語言 的運用與媒體影像及先前的學習結果形成了 學生在進入課堂前的先備概念。這些先備概 念將顯著地影響學生對課堂所教的概念的接 受與了解，換句話說，學生以他們的已知來 形成他們的新理解 (NRC, 2005)。因此要探 討學生對「失重」的概念，就必須要先了解 學生對「重量」與「重力」的概念。 (一)重量的概念發展：直觀科學 重量概念的發展很早，即使是三歲幼兒 已能正確辨識物體的輕重，並了解物體重量 所產生的效應，如「重就搬不動」；但是對 於很輕的物體，大多數的兒童會認為沒有重 量，有些則由於語言的邏輯思考認為「沒有 重(不是重量為零)」，有些更指出具有「輕 量」(莊麗娟，2007)。Galili和Bar (1997)探索 五到十六歲兒童的重量概念發展，發現在幼 兒時期他們就已經由直觀建構了「重量是下 壓的力(weight-is-a-pressing-force)」、「重量

為 重 的 物 體 所 獨 具 (weight-is-possessed-exclusively-by-heavy-obj ects) 」 、 「 懸 空 的 物 體 沒 有 重 量 (suspended-substances-are-weightless) 」 以 及 「重量是拿或搬動物體所感覺到的『重性』 (weight-is-heaviness-to-hold/move)」等概念。 兒童的確從他們的日常生活及遊戲中， 逐漸地由親身體驗，甚至經由語言與媒體影 像進行理解，並做簡單的推論，建構他自己 的重量概念。 (二)重力的概念發展：世俗科學及學校科學 沒有研究支持兒童的重力概念來自直觀 的建構，不過Kikas和Hannust(2002)對五和七 歲的兒童所做的研究顯示，兒童可經由教學 獲得重力(地球引力)概念，但是這個重力概 念卻是基於原有的直觀和世俗概念建構而 來，因此有些兒童認為重力並非作用在任何 物體，只有和地表接觸的才受重力作用，例 如飛鳥、飛機就不受重力影響。經過更進一 步的解釋後，兒童可以克服這個混淆，有些 甚至建構出「沒有地球引力的吸引，每一樣 東西都會漂浮到空中。」但是這個概念可能 影響後來對「失重狀態」的理解，形成「飄 浮在空中的物體沒有受到地心引力的作用」 的推論。 (三)國中小階段的重量與重力教學 重量的教學在國民中小學課程綱要 (教 育部，2003) 中主要安排在數學，遍及二至 七年級，課程綱要及教學現場 (如，姚如芬、 林佳穎，2003) 的教學順序符合重量概念的 直觀發展，先透過輕重的感覺、接著作直接 和間接的「比較」，然後再運用「測量」來 建構重量概念；在自然科學領域中，一、二 年級配合數學，由察覺物體的輕重來認識重 量，但是到了五、六年級，能力指標則將重 量定義為「重量就是物體所受到的重力，重 力會使物體落下。」這樣定義的用意，可能 是要告訴學生重量的來源是重力，而且讓學 生了解重力對物體產生的效果。不過這樣的 定義將重量等於重力，讓學生把直觀發展而 來的重量概念與教學而來的重力概念劃上等 號，給了學生以推論來發展出更多另有概念 的機會。 (四)學生的重量與重力另有概念 隨著年齡的增長，學生的重量與重力概 念越來越趨向學校科學發展，不過對中小學 生及大學生的研究(如: 王俊貴，2002；余秀 麗和譚克平，2005；張月霞，2005；張良程， 2003；廖婉君，2002；Hestenes, Wells, & Swackhamer, 1992; Palmer, D., 2001; Sharp & Sharp; 2007) 發現、有些迷思概念卻仍然持 續到高中甚至大學，如「上升的物體不受重 力」、「靜止的物體不受重力」、「越重的 物體掉得越快」、「在水中物體重量變輕， 所受的地心引力變小」、「重力需要空氣媒 介，真空中的物體不受重力作用，大氣層之 外物體不受重力，大氣層之內才有重力作用」 等；有些則是後來才出現，如「重力是長距 離的作用力，在大距離時比較強 (Treagust & Smith, 1989)」。

Kjærnsli, Angell, & Lie (2002) 分析國際 性測驗TIMSS中十三歲學生(七至八年級)有 關蘋果從樹上掉落所受重力的情形，發現雖 然答對率各國不同，不過學生的迷思概念則 普偏一致，各國答錯最多的選項均一樣，顯 示25%-36%的學生認為重力只作用在蘋果掉 落的過程中，而靜止的蘋果不受力，diSessa (1993) 主張這是因為學生將重力視為「運動 的力(moving force)」。另有6%-11%的學生則 認為重力只作用在靜止的物體上，而蘋果在 掉落過程不受重力作用，這個想法可能來自 「重量就是重力的大小」的教學與「懸空的 物體沒有重量」的直觀概念。 (五)學生的失重概念

日常經驗體驗失重的機會不多，失重概 念的發展來自世俗及學校科學，以及根據既 有概念所作的推論。Gürel & Acar (2003) 以 電梯鋼繩斷裂而自由落下時，電梯中站在磅 秤上的人其磅秤讀數的問題，調查高中和大 學生的失重概念，結果發現：近半數的學生 認為重量會變小，一成多認為會變大，認為 重量變為零的只有兩成，但是連理由都答對 的，高中生沒有，大學生則只有2%，而在錯 誤的理由中最常被提到的是電梯的加速度降 低了重力的作用。 這可能是來自教學，少部分來自搭電梯 的經驗，當電梯向下加速時感覺體重變輕， 而重量就是重力的概念導致重力變小的結 論。 不過也有學生持相反看法，認為會使得 重力加速度增加，顯然大部分學生並未具備 清晰的重量與重力概念。

二、高中教科書的重量與重力之定義

市面上的高中教科書，對重量的定義或 說明有三類： (一)重量即重力 此種說法有兩種方式，一種是以重量來 說明重力，小學的教學常採用這種方式，因 為兒童的重量概念發展先於重力；另一種是 以重力來說明重量，許多國中教科書(如，鄧 美貴, 2004)及高中教科書採用這種方式，直 接指明物體所受的重力稱為物體的重量。例 如： 地球對物體的引力稱為物體所受的 重力，而地面上物體所受的重力常 稱為地面上物體的重量，W=mg。(楊 宗哲，2006：34) 上面的說明把重量限制在地面上，這樣的說 法可能加強了「懸空的物體沒有重量」的直 觀概念。有些課本說明了重量的觸感 (tactile) 經驗，不過並未使用這個經驗來定義重量。 例如： 「重力」源自萬有引力，牛頓發 現：「萬物之間存在著一種引力」… 這也是我們常把物體受地球的萬 有引力稱為「地心引力」的緣故。 物 體 受 到 的 地 球 引 力 稱 為 「 重 力」。當我們想把物體由地面拿起 來時，需要克服這個重力，也就是 我們所稱的「重量」。(陳文典， 2007：38) 上述的說明指出重力就是地球引力(或稱地 心引力)就是重量，可是這樣的說法在解釋 「失重」時就遭遇了困難。教科書在解釋「失 重」時採用視重，換句話說，採用了重量是 接觸力的定義。 (二)重量重力的大小 有些教科書採用了重力的大小就是重 量，而讓重量變成了純量。例如： 物 體 的 重 量 來 自 地 球 引 力 的 作 用，所以地球引力又稱為重力，此 力恆指向地心。…質量為m的物體 所受的地球引力大小，即其重量 W，可以下式表示之： W = mg [W: 重力(N)；m: 物體質量(kg)； g: 重力加速度(m/s2)] …重量…代表物體所受地球引力 的大小…物體的重量W可以寫成 下式: W = mg = ₂

r

Mm

G

[W: 物體重量；M: 地球質量；m: 物體質量；r: 物體和地心間的距 離]

(林明瑞，2008：36-38) 可是這仍然無法釐清「失重」的概念，因為 如果失重時意謂重量為零，則根據上述公 式，質量不為零，則g為零，亦即重力為零； 如果重力不為零，則表示重量亦不為零，所 以仍然需要採用「視重」來解決這個問題。 (三)重量是作用於體重計的力 有些教科書對重量的概念著墨較多，而 且從重量的測量開始說明。例如： 當我們站在體重計上，同時會受到 地球的重力及體重計的正向力作 用，這兩個力大小相等，方向相反。 體重計所顯示的重量，也是我們作 用於體重計上的力，此力與地球施 於我們的重力是一樣大的。(褚德 三，2006) 如果重量是我們作用於體重計上的力，那麼 重量就是正向力的反作用力，當正向力不存 在，重量也不存在，這樣的角度有利於失重 概念的解釋： 因為當我們與體重計都以相同的速 度與加速度下落，兩者間不存在因 擠壓所造成的正向力，因此體重計 將無法顯示我們的重量。這樣的結 果，就彷彿是我們失去了重量一 般，故稱這種現象為失重。(褚德 三，2006) 不過「彷彿是我們失去了重量」這句話，可 能讓學生以為重量並未失去，只是好像失 去，因為磅秤測不到，實際上還有重量，那 麼這個重量會是甚麼？ 有些教科書則指出： 人施給磅秤一向下的力，此力的大 小即磅秤的讀數，即體重。…因此 人的體重就是所受地球引力的大 小。(林明瑞，2008) 這種說法將重量視為純量。這類教科書雖然 介紹了重量的操作型定義，卻仍然將重量等 於重力的大小。

三、科普雜誌的重力定義

有別於教科書把重力等於地球引力， 「Newton量子科學雜誌」把重力定義為： 物體牽引其他物體的力量就是「萬 有引力」。物體承受來自地球的萬 有引力及地球自轉的離心力的合 力，就是「重力」。(淺島誠、古川 義純、山岸明彥，2008：71) 這樣的定義引進了離心力，保留了重力 即 重 量 的 觀 點 ， 也 吻 合 了 失 重 狀 態 (weightlessness)又稱無重力狀態(zero gravity) 的說法，但是卻有下列缺點：第一，與學校 科學違背；第二，離心力是假力，與一個不 存在的力來求合力，並不合理；第三，除非 不在重力場中，否則失重狀態的物體所受合 力並不為零。因此這樣的定義並不合適，可 能造成學生更多的迷思概念。

四、小結

國中小九年一貫課程綱要所採取的重量 與重力概念(其中失重概念並未包含於課綱) 研究者以圖1(a)來表示，圖中實線表示概念 最先來自個人經驗，即直觀科學，虛線表示 來自教學，即學校科學。重量概念的發展起 始於學生早期的觸感經驗(莊麗娟，2007)， 因此以作用於磅秤的力來解釋重量，亦即以 操作型定義來定義重量，符合學生的概念發 展。不過從概念圖可以看出要把重量和重力 直接相等，會出現接觸力等於超距力的矛盾。

而高中教科書要談失重概念，不能再忽 視這個矛盾，否則為了維持重量即重力的概 念，只好把磅秤測得的重量視為視重，如圖 1(b)，如此一來重量卻脫離了原來的概念發 展過程，脫離了學生的經驗，而純粹變成了 學校科學中的一個抽象物理量。然而學生的 概念常常不只是學校科學的概念，而是混雜 著直觀科學與世俗科學，重量與重力的概念 也不例外。雖然教科書試圖將重量從觸感經 驗切割，但是學生對根深蒂固的經驗卻很難 割捨。 有鑑於此，本研究將以失重時人的重量 及其所受的重力，來檢驗高中學生的失重概 念。 下落 經由觸覺 _經由教學 經由視覺 靜止 即(?) 物體重性 Heaviness 狀態 輕重 超距力 接觸力 重力 重量 測量 質量 為 作用 經由 感覺到 用於 得到 即 即 因為 失重 為零 不變 作用 視為 _受 作用 為 受 圖 1(a)：國中小課程綱要的重量與重力概念圖 重量概念由觸覺經驗發展而來，重力概念則由視覺經驗再經直接教學而來，但是「重量即 重力」卻產生接觸力等於超距力的矛盾。(本圖為研究者的詮釋，不代表課綱觀點) 物體重性 Heaviness 經由觸覺 _經由教學 經由視覺 靜止 即 狀態 輕重 超距力 接觸力 重力 視重 測量 下落 質量 為 受 經由 感覺到 用於 得到 即 即 因為 失重 為零 不變 計算 _受 重量 作用 作用 作用 為 計算 ? 圖 1(b)：高中教科書的重量與重力概念圖 將重量由觸覺經驗切割分離出來，並將其等同於教學而來的重力，至於原來的重量則以視 重來取代，然而視重與重量之間的關係卻曖昧不明。(本圖為研究者的詮釋，不代表教科 書作者觀點)

參、研究方法

由於教科書以電梯自由落體來解釋失 重，而且學生也練習過許多「電梯失重」的 題目，為了避開練習強記的影響，所以另以 失重飛行作為研究的背景。 本研究以量化的調查研究為主，以質性的個 案訪談為輔。研究分為三階段(如圖2)，分別 說明於下。

一、問卷發展：

(一)理論基礎 Treagust(1986)指出，研究者對於學生概 念的診斷，最常採用的方法有晤談及選擇式 測驗。我國在 2000 年至 2003 年進行的大型 整合型研究—「科學概念學習研究」中，用 來診斷學生概念的工具就是兩階層(two tier) 選 擇 式 測 驗 ( 郭 重 吉 ， 2005) 。 依 據 Treagust(1986, 1988)的建議，兩階層選擇式 測驗的第一層是「事實」階層，用來測驗學 生的事實知識，第二層是「理由」階層，用 來確認學生的解釋、推理或其心智模式，而 其 各 誘 答 選 項 則 是 晤 談 學 生 而 來 的 答 案 (如，林明良、陳忠志，2002; Chen, Lin, & Lin, 2002; Tsai & Chou, 2002)。這樣發展出來的工 具包含了晤談的優點，也提供了大量施測的 可行性，有利於全盤了解全班學生所持有的 概念及其概念背後的理由。 然而選擇題會因猜測而降低試題信度，而信 心加權(confidence weighting)可以彌補這個 缺點。自從1930年代提出「信心加權」迄今， 已經演變出各式各樣的運用，其核心就是讓 受試者評定對自己答案的信心(Echternacht, 1971)。許多研究指出，自我信心加權的評分 方式可以大幅提升試題信度，並且比傳統的 評分方式，對學生的課業表現有更高的相 關，換句話說，信心加權評分更能診斷出學 生 的 概 念 理 解 (Ahlgren, A. 1969; Garvin, 1972; Pugh & Brunza, 1975; Stankov &Crawford, 1997)。因此開始有研究者將自我 信心加權評分加入二階層診斷測驗而形成三 階層測驗(如，Kaaltakçi, & Didiş, 2007)。

不過，單選式的選擇題卻限制了學生只 能在選項中選取一個答案，事實上常常會在 開放式問卷 「失重」概念 兩段式測驗 前、後測問卷

階段 I:問卷發展 階段 II:問卷施測 階段 III:個案訪談

試測 z 科學教師 z 國立理學院 大學生 z 公立高中 自然組學生 試測 z 公立高中 自然組學生 正式施測 z 公立高中 自然組學生 統計分析 晤談 資料詮釋 文獻探討 圖 2：研究架構

不同選項中猶豫不決。許多研究(如，Gibert, Osborn, & Fensham, 1982; Tsai et al.,2007; Tytler, 2000)發現，學生的概念往往模糊不 清，甚至存在著相互衝突的觀點，隨著與不 同的診斷工具交互作用，會呈現出其中一種 型式的概念理解，因此會出現學生在與教學 情境相同的測驗中似乎有正確的概念，但是 在運用到日常情境的測驗中就出現完全矛盾 的概念(蔡嘉興，2007; Tsai, Chen, & Chou, 2006)。因此本研究在理由階層，將單選改成 對每個誘答選項進行是非判斷，作答者並對 這個選項的說服力予以評分(0 表示錯誤，完 全無說服力；5 表示可以肯定是正確的，說 服力最高)，如此可以顯示學生對該選項的同 意程度，教師則可理解學生的「概念組成」， 並且可以了解哪些理由對哪些學生最具說服 力，可以做為概念改變教學的參考。 (二)問卷設計 根據上述分析，本研究的概念診斷工具 採用二段四階層測驗設計，分前、後測問卷。 前測問卷第一段測量「事實」選項，並對作 答進行信心加權評分，第二段為「理由」部 分，採開放式問卷，同時也對作答進行信心 加權評分；後測問卷第一段則為「理由」部 分，採是非題，學生就每項理由判斷是非， 若為「是」則繼續對其說服力評分(1 分最低， 5 分最高，0 分為「非」)，第二段為事實選 項，並對作答進行信心加權評分。後測問卷 讓學生先評斷理由，是希望引發學生的既有 概念來判斷事實選項的答案。發展完成的後 測問卷見附錄，第一題有關失重概念的理由 選項如表 1，第二題有關失重時機的理由選 天文物理學家霍金 (Stephen Hawkin) 罹患肌萎縮性脊髓側索硬化症而被困在輪 椅四十年，終於在 2007/4/26 日脫離輪椅自由自在飄浮了八次，每次約三十秒，共享 受了四分鐘的失重狀態。著地後他很高興的說：太空，我來了！ 失重狀態是由波音七二七噴射客機在大西洋上空八千五百公尺到六千公尺間做 「拋物線」波浪狀飛行所產生。也就是飛機飛行路線由數個向下開口和向上開口的 拋物線所組成(如上圖，修改自 BBC, 2007)。 1. 在波音七二七做拋物線失重飛行時，所謂的失重狀態，是真的所受重力為零嗎？ 2. 請看上頁圖，你認為在哪些(或哪一)段飛行時間中，可以體驗到失重狀態？ 圖三 失重概念問卷的背景資料與問題 圖 3：失重概念問卷的背景資料與問題

項如表 2 所示，問卷的開發過程(見圖 2 階段 I)說明於下。 本研究工具避開學生已學過並練習過 的電梯自由落下而失重的題目，而以霍金體 驗失重飛行的新聞(彭淮棟編譯，2007)為背 景(如圖 3)，先開發開放性試題，先後對中學 科學教師 23 人、國立大學理學院學生 46 人、 及公立高中自然組學生 32 人試測，再根據作 答資料整理出學生可能作答的選項並加入文 獻探討所獲得的資料，以及教師可能用來解 釋的理由，發展成「事實—理由」兩段四階 層測驗，然後再以公立高中高二自然組學生 31 人進行試測，以測驗結果修訂試題。全份 試題測驗學生的失重概念以及產生失重的時 機，試題並經物理教育專家二位及高中物理 教師五位進行審核，以建立內容效度。 表 1：第一題「失重概念」的理由 編號 理由 b101.失重表示失去重量，所以飛機艙內的人所受重力為零。 b102.失重時人會漂浮，表示人未受到重力的作用。 b103.失重時人會漂浮，表示人所受的外力合力為零。 b103P.飛機在最高點失重時，這時鉛直方向的速度為零，表示不受力。 b104.飛機在最高點失重時，這時鉛直方向加速度為零，表示不受力。 b105.像太空梭繞地球飛行，此時重力正好當作向心力，而呈失重狀態，如太空漫步的太 空人，其實他跟太空梭一起往下掉，只是下降的幅度正好等於地球的弧度變化。 b106.因為飛機和人都還在地球重力場中，而且距離地心幾乎不變(可忽略)，所以受有重 力且大小與失重前相當。 b107.失重並不是真的零重力，也不是外力合力為零，而是仍受重力作用，但在自由落下 這段時間內，人和地板也以相同的重力加速度在往下掉，因此感受不到重力。 b108.失重前人感受到飛機地板的支撐，所以有重量，當飛機引擎不再加速，此時飛機和 人都只受到向下的重力加速度 g 的作用，人相對於飛機的加速度為零，地板不需要 再支撐人，所以人感覺失重。 b109.飛機有水平的向前加速度，所以在飛機上人會感受到向後的加速度，也就是向後的 力，加上原來向下的重力加速度產生的重力，兩力的合力就是人感受的重力。 b110.飛機作拋物線飛行，表示飛機在水平方向是等速運動，就像只受重力作用的拋體運 動一樣，飛機和人都受重力作用。 b111.飛機並非在真正的無重力環境(如無重力場的外太空)，而是製造出無重力狀態，因 此所受重力要比失重前小才浮得起來。

二、問卷施測：

施測樣本為方便取樣，對象為已學過力 學(高二物理上冊，包括失重概念)的公立高 中學生三班96人。本研究理由部分施測的信 度Cronbach’s α為0.72，大於可接受的最小信 度值0.70 (Gay, 1992)，表示本次施測具有相 當的內部一致性，學生並非隨機猜測作答。

三、個案訪談：

為更深入了解「理由判斷」對學生的「失 重」概念的影響，研究者進一步挑選自願學 生12位，以前述問卷為本，進行訪談，並就 訪談 資料以及上述統計資料進行詮釋。

肆、結果與討論

儘管學生已學過重量、重力及牛頓運動 定律的概念，並且學過失重狀態的現象，但 是仍有超過半數的學生擁有與科學概念不同 的失重概念，而且七至八成的學生無法完全 正確判斷失重的時機。施測結果分別說明於 下：

一、學生對失重意義的看法

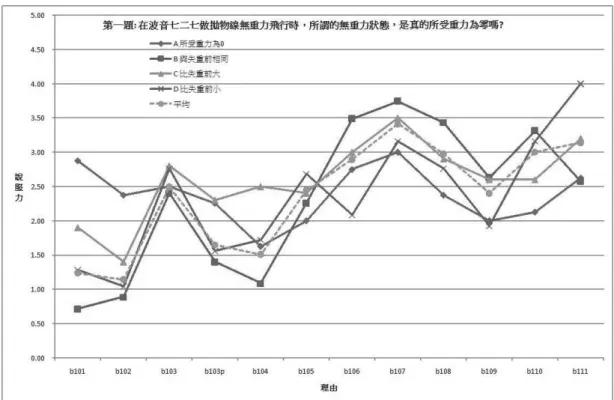
問卷第一題調查學生的失重概念，詢問 表 2：第二題「失重時機」的理由 編號 理由 b201.在 C 時飛機掉下來，只有向下的重力加速度，類似電梯失速下墜，人會覺得失重。 b202.在 D 時，飛機往下的加速度正好等於 g 值，此時才會有失重感覺。 b203.在 D 時，飛機的加速度向上，也就是飛機的鉛直速度要越來越小。 b204.在 D 斜率最大，表示加速度大小最大，而且斜率為負值，表示飛機向下加速，所以 產生失重狀態。 b205.在 B 和 C 時，從向下開口的飛行拋物線軌跡得知，此時飛機作只有向下加速度，沒 有水平加速度的拋體運動，此時飛機和人的加速度都是 g，所以飛機和人以相同的 加速度上升後下降，人對飛機的相對加速度為零，形成失重。 b206.在 B 和 C 兩段，類似以地心為中心的圓周運動，此時所受的重力作為向心力，就像 繞地球作太空漫步的太空人處在失重狀態。 b207.在 BCE 能體會失重，因為這三段是飛機迅速改變方向的段落，因人體仍有原方向的 切線速度，但飛機卻向另一方向，故可達失重。 b208.飛機一直有水平加速度，所以不管垂直方向加速度如何改變，都不可能體驗失重狀 態。 b209.只有飛機在最高點時，鉛直速度為零，此時才是失重狀態。 b210.像六福村的大怒神一樣，在自由落下的過程中體驗失重。 b211.像坐在雲霄飛車，在到達頂端前後那段可以體驗失重。

「飛機失重飛行時，所謂的失重狀態，是真 的所受重力為零嗎？」 以下將學生依施測結果(見表 3、圖 4 及 圖 5)分五類，分別說明如下： (一)失重時所受重力為零 (選項 A) 前測中有 14.6%的學生具有此想法，後 測則減為 9.6%。整體而言，這類型學生最認 同的理由依序為： 1. 失重並不是真的零重力，也不是外力合力 為零，而是仍受重力作用，但在自由落下 這段時間內，人和地板也以相同的重力加 速度在往下掉，因此感受不到重力。(b107) 2. 失重表示失去重量，所以飛機艙內的人所 受重力為零。(b101) 3. 因為飛機和人都還在地球重力場中，而且 距離地心幾乎不變 (可忽略)，所以受有重 力且大小與失重前相當。(b106) 4. 飛機作拋物線飛行，表示飛機在水平方向 是等速運動，就像只受重力作用的拋體運 動一樣，飛機和人都受重力作用。(b110) 其中理由 b101 與 b107、b106、b110 相互矛 盾，檢查個別學生的作答情形，發現學生的 作答確實存在這個矛盾，顯示學生對地球引 力、重力及重量的概念混淆不清，例如有學 生說： 在高空中地心引力已有減少，因為 GMm/r2，r 變大，再使用高速噴射 機產生向下加速度，使內部的人產 生無重力的感覺。(s1517p1) 學生的概念呈現兩個問題：1. 學生未覺 察到 G 值很小，所以即使在高空中 r 變大， 但重力減少有限，換句話說學生未能了解這 個數學公式的數值大小；2. 學生認為向下加 速度使重力減小這與 Gürel & Acar (2003)的 發現一致，這個想法來自失重會飄浮的意 像，他說「向下加速度使人飄起來，重量變 零。」而重量即重力，所以所受重力為零， 這個觀點與另一個學生的看法：「失重就是無 重量，就是所受重力為零。(s1406p1)」異曲 同工。 值 得 注 意 的 是 ， 本 類 型 學 生 對 理 由 b103p 的說服力評分均約 2.3，顯示多數具有 「最高點時鉛直速度為零，所以不受力」的 迷思。 (二)失重時所受重力不變(選項 B) 前測只有 36.6%具有這個與現行的學校 科學概念相同的想法，認為飛機在失重飛行 時，艙內的人所受重力仍與失重前相同，在 提供理由判斷的後測中則提高至 44.6%。整 體而言，這類型學生最認同的理由依序為 1. 失重並不是真的零重力，也不是外力合力 為零，而是仍受重力作用，但在自由落下 這段時間內，人和地板也以相同的重力加 速度在往下掉，因此感受不到重力。(b107) 2. 因為飛機和人都還在地球重力場中，而且 距離地心幾乎不變(可忽略)，所以受有重 力且大小與失重前相當。(b106) 3. 失重前人感受到飛機地板的支撐，所以有 重量，當飛機引擎不再加速，此時飛機和 人都只受到向下的重力加速度 g 的作用， 人相對於飛機的加速度為零，地板不需要 再支撐人，所以人感覺失重。(b108) 4. 飛機作拋物線飛行，表示飛機在水平方向 是等速運動，就像只受重力作用的拋體運 動一樣，飛機和人都受重力作用。(b110) 亦即他們可以區分重力是物體所受的地球引 力，而失重不是失去重力而是失去重量。例 如有學生說： 地球的引力一樣存在，所以 W=mg， g 沒變，所以重力沒變。(s1131p1) 值得注意是，上述學生把 W 視為重力而非教

科書所指的重量。至於為何失重，他的解釋 是： 相對的關係來看，飛機向下，和重 力方向相同，移一公尺，人也一樣。 (s1131p2) 換句話說，人得不到支撐，所以失重。 (三)失重時所受重力會變大(選項 C) 前測中有 11.0% 認為所受重力大於失 重前，後測則為 12.0%。整體而言，這類型 學生最認同的理由依序為： 1. 失重並不是真的零重力，也不是外力合力 為零，而是仍受重力作用，但在自由落下 這段時間內，人和地板也以相同的重力加 速度在往下掉，因此感受不到重力。(b107) 2. 飛機並非在真正的無重力環境(如無重力 場的外太空)，而是製造出無重力狀態，因 此所受重力要比失重前小才浮得起來。 (b111) 3. 因為飛機和人都還在地球重力場中，而且 距離地心幾乎不變(可忽略)，所以受有重 力且大小與失重前相當。(b106) 其中 b111 及 b106 均與其主張矛盾，晤談結 果有些學生說是猜測，有些學生說是看錯題 目，他們的答案是比失重前小，因此本類學 生可能少於一成。不過仍有學生以為失重時 會飄浮，雖然感覺不到重力，但是在下墜， 距離地心變近，所以所受重力變大，這個想 法仍然是因為對 GMm/r2 的數值大小沒有感 覺。 還有二項理由： 4. 飛機在最高點失重時，這時鉛直方向速度 為零，表示不受力。(b103p) 5. 飛機在最高點失重時，這時鉛直方向加速 度為零，表示不受力。(b104) 其他各類學生對上述兩項理由認同低，但本 類學生卻持相反觀點，顯示有些學生具有最 高點不受力的迷思，而下墜時失重(b107)， 但受力變大所以所受重力變大。 值得注意的是，從對理由的評分來看(見 圖 5)，本類型學生雖然對科學概念的評分較 高，但對其他另有概念的評分也多在 2.3 以 上，顯示本類型學生具有最多的迷思概念。 (四)失重時所受重力會變小(選項 D) 前測中亦有 36.6%認為所受重力比失重 前小，後測則減少至 31.1%，這是佔比例最 大的另有概念。整體而言，這類型學生最認 同的理由依序為： 1. 飛機並非在真正的無重力環境(如無重力 場的外太空)，而是製造出無重力狀態，因 此所受重力要比失重前小才浮得起來。 (b111) 2. 失重並不是真的零重力，也不是外力合力 為零，而是仍受重力作用，但在自由落下 這段時間內，人和地板也以相同的重力加 速度在往下掉，因此感受不到重力。(b107) 3. 飛機作拋物線飛行，表示飛機在水平方向 是等速運動，就像只受重力作用的拋體運 動一樣，飛機和人都受重力作用。(b110) 亦即他們並未區分重力與重量，所以失重是 重力變小的結果。例如有學生說： 所受重力比失重前大或等於，應該 是不會漂浮的，也不會完全沒有重 力，因為最少還是會有地心引力的 影響。(s1105p1) 受的重力比較小，就比較輕，就浮 起來了!(s1113p1) 許多這類型學生都以為失重就是飄浮，並且 相信重量要變輕才會浮起來，所以推論所受 重力變小，有少數學生則以離地心較遠所以 重力變小來解釋。 (五)其他 有極少數學生以「真空中無重力，在大

氣中才有重力」來解釋失重，如： 所謂無重力應該不是沒有重力，因 為飛機仍然在大氣層內。(s1103p1) 研究者繼續追問是否在大氣層外就不受 重力，學生回答：「是，因為大氣層外沒有空 氣。」這個看法與「真空中的物體沒有重量 或不受重力」的另有概念吻合。 從以上的討論中發現學生未能正確選擇的原 因，一大部分可能與「以重力解釋重量」的 教學有關，這樣的教學讓學生將重力與重量 畫上等號，因此認為失去重量就是失去重 力，或是混淆重力、重量及地球引力的概念。

二、學生對失重時機的判斷

問卷第二題詢問「圖 3 中飛機失重飛行 時，哪一段或哪些段時間會產生失重狀態？」 以下將學生依施測結果(見表 3 及圖 6) 分成五類，分別說明如下： (一)失重只發生在飛機上升至最高點前 這段時間(選項 B) 前測 6.0%，後測 7.2%的學生作這項選 擇。這類型學生最認同的理由依序為： 1. 在 C 時飛機掉下來，只有向下的重力加速 度，類似電梯失速下墜，人會覺得失重。 (b201) 2. 在 B 和 C 時，從向下開口的飛行拋物線 軌跡得知，此時飛機作只有向下加速度， 沒有水平加速度的拋體運動，此時飛機和 人的加速度都是 g，所以飛機和人以相同 的加速度上升後下降，人對飛機的相對加 速度為零，形成失重。(b205) 3. 只有飛機在最高點時，鉛直速度為零，此 時才是失重狀態。(b209) 4. 像坐在雲霄飛車，在到達頂端前後那段可 以體驗失重。(b211) 其中 b209 顯示學生具有在最高點時「鉛直速 度為零，所以加速度為零」的迷思。學生認 為快到最高點時，加速度越來越小，表示受 力越來越小而失重。b211 是雲霄飛車的類 比，可用來強化選擇 B 的信心。 (二)失重只發生在飛機從最高點落下這段時 間(選項 C) 前測 9.6%，後測 14.5%的學生作這項選 擇。這類型學生最認同的理由依序為： 1. 在 C 時飛機掉下來，只有向下的重力加速 度，類似電梯失速下墜，人會覺得失重。 (b201) 2. 在 B 和 C 時，從向下開口的飛行拋物線 軌跡得知，此時飛機作只有向下加速度， 沒有水平加速度的拋體運動，此時飛機和 人的加速度都是 g，所以飛機和人以相同 的加速度上升後下降，人對飛機的相對加 速度為零，形成失重。(b205) 3. 像坐在雲霄飛車，在到達頂端前後那段可 以體驗失重。(b211) 他們只是以類比來做判斷，並不見得能說出 失重原因，例如有學生就以慣性來解釋，他 說： 因為上升時慣性運動會向上，然後 突然向下，一上一下之間可以取得 平衡，向上的力會抵消向下的力， 出現失重狀態。(s1124p2) (三)失重只發生在飛機越過反曲點繼續下落 這段時間(選項 D) 前測 20.5%，後測 18.1%的學生作此選 擇，這是被學生選擇次多的非科學觀點選 項。這類型學生最認同的理由依序為 1. 像六福村的大怒神一樣，在自由落下的過 程中體驗失重。(b210) 2. 在 D 時，飛機往下的加速度正好等於 g 值，此時才會有失重感覺。(b202) 3. 在 C 時飛機掉下來，只有向下的重力加速

度，類似電梯失速下墜，人會覺得失重。 (b201) 4. 在 B 和 C 時，從向下開口的飛行拋物線 軌跡得知，此時飛機作只有向下加速度， 沒有水平加速度的拋體運動，此時飛機和 人的加速度都是 g，所以飛機和人以相同 的加速度上升後下降，人對飛機的相對加 速度為零，形成失重。(b205) 這類型的學生也是以下墜類比來做判斷，而 且他們不認為在這段時間飛機的加速度是向 上 (對「b203 在 D 時，飛機的加速度向上， 也就是飛機的鉛直速度要越來越小」評分很 低)，例如有學生說： 往下時，會有一股向上的力量，因 與地心引力作用相反，應該會飄起 來，就跟坐自由落體一樣，向下衝 時，會整個離開座位。(s1105p2) (四)失重只發生在上升到頂點前及從頂點下 落時這段時間(選項 BC) 前測 30.1%，後測 20.5%的學生選擇這 個符合科學概念的選項。這類型學生最認同 的理由依序為： 1. 在 B 和 C 兩段，類似以地心為中心的圓 周運動，此時所受的重力作為向心力，就 像繞地球作太空漫步的太空人處在失重 狀態。(b206) 2. 像六福村的大怒神一樣，在自由落下的過 程中體驗失重。(b210) 3. 在 C 時飛機掉下來，只有向下的重力加速 度，類似電梯失速下墜，人會覺得失重。 (b201) b206 是圓周運動的類比，後兩者是下墜的類 比。許多學生雖然答對了 BC，但是卻未能 指出正確的理由，例如 b206 就是不正確的類 比，另外有些學生在晤談時就以「離地最遠 (如 s1103p2)」來解釋，有些則以「直覺(如 s1401p2)」來回答。另有學生說： 我覺得這架以拋物線前進的飛機 有點類似在作圓周運動，當飛機飛 到 B、C 段的時候會產生一個很大 的離心力，由於 B、C 段離地心較 遠，所以飛機飛到 B、C 段時產生 的離心力會讓人覺得處於無重力 狀態。(s1426p2) 學生的這段解釋混合了學來的離心力的解釋 及「離地心較遠」的素樸解釋。 (五) 失重只發生在從頂點下落到接近最低 點前這段時間(選項 CD) 前測 22.9%，後測 25.3%的學生作此選 擇，這是被學生選擇最多的非科學觀點選 項，在後測則超越 BC 成為選擇最多的選 項。這類型學生最認同的理由依序為： 1. 像六福村的大怒神一樣，在自由落下的過 程中體驗失重。(b210) 2. 在 C 時飛機掉下來，只有向下的重力加速 度，類似電梯失速下墜，人會覺得失重。 (b201) 3. 在 D 時，飛機往下的加速度正好等於 g 值，此時才會有失重感覺。(b202) 4. 在 D 斜率最大，表示加速度大小最大，而 且斜率為負值，表示飛機向下加速，所以 產生失重狀態。(b204) 前兩者是下墜的類比，後兩者說明學生誤認 為 D 段飛機的加速度仍然向下。 以上的分析發現學生最常以類比來考量 失重的時機，而不常從重量的測量觀點來考 慮失重，所以數據顯示在後測中只有 8.4%的 學生兩題均作答正確，卻有 16.9%的學生認 為「失重時所受重力不變，失重時機是飛機 向下飛行的時候」。 這是在教學上把重量與重力連結而與觸感經 驗切割的結果，使得學生對失重的考量由重

力概念開始再與既有的重量概念連結，例如 「物體下墜時重力變小而失重，所以失重時 機在物體下墜時」。 表 3：學生在「失重概念」及「失重時機」作答分佈百分比 前測 可以體驗到無重力狀態的飛行時段 飛機艙內的人 所受重力 A B C BC* CD BCD D AD BD DE BDE ABCD 累計 % A 為零 1.2 2.4 1.2 4.9 2.4 1.2 0.0 1.2 0.0 0.0 0.0 0.0 14.6 B* 與失重前相同 1.2 1.2 4.9 8.5 8.5 0.0 9.8 1.2 0.0 0.0 0.0 1.2 36.6 C 比失重前大 1.2 1.2 0.0 6.1 2.4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 11.0 D 比失重前小 0.0 1.2 3.7 9.8 8.5 0.0 11.0 0.0 0.0 2.4 0.0 0.0 36.6 E 其它 0.0 0.0 0.0 0.0 1.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.2 累計% 3.6 6.0 9.6 30.1 22.9 1.2 20.5 2.4 0.0 2.4 0.0 1.2 100 後測 可以體驗到無重力狀態的飛行時段 飛機艙內的人 所受重力 A B C BC* CD BCD D AD BD DE BDE ABCD 累計 % A 為零 0.0 3.6 2.4 0.0 1.2 1.2 1.2 0.0 0.0 0.0 0.0 0.0 9.6 B* 與失重前相同 0.0 2.4 4.8 8.4 16.9 1.2 7.2 0.0 2.4 0.0 0.0 1.2 44.6 C 比失重前大 1.2 0.0 2.4 3.6 1.2 0.0 2.4 1.2 0.0 0.0 0.0 0.0 12.0 D 比失重前小 0.0 1.2 4.8 8.4 4.8 2.4 7.2 0.0 0.0 1.2 1.2 0.0 31.3 E 其它 0.0 0.0 0.0 0.0 1.2 0.0 0.0 1.2 0.0 0.0 0.0 0.0 2.4 累計% 1.2 7.2 14.5 20.5 25.3 4.8 18.1 2.4 2.4 1.2 1.2 1.2 100 *表示正確答案 圖 4：學生對失重飛行時，機艙內的人所受重力大小的回答分佈情形

圖 5：不同理由(見表一)對不同失重概念(第一題的事實選項)學生的說服力

三、討論

以下就本研究的結果與發現提出五點 做更進一步的討論： (一) 學生的失重概念出現科學概念與另有 概念混雜的情形 從學生所認同的失重概念的理由可以 看出(見圖 5)，除了做出正確判斷的學生以 外，其他學生雖然在科學概念的評分也較 高，但是在其他另有概念的評分也偏高，顯 示學生的概念出現科學概念與另有概念混雜 的情形，甚至相互矛盾的概念共存的狀況， 這與 Palmer (2001) 的研究指出「多數學生的 重力概念同時展現可接受的科學概念及另有 概念」相吻合。 (二) 學生不習慣使用重量操作型定義而習 慣使用「重力即重量」來解釋失重 整體而言，學生最認同的失重理由是： 「人和地板也以相同的重力加速度在往下 掉，因此感受不到重力(b107)」。但是對「人 對於飛機的相對加速度為零，地板不需要再 支持人，所以人感覺失重(b108)」的說服力 評分卻相對偏低，其實這兩項理由前半部的 說法一樣，只有後半部時，前者用重力的說 法，後者則使用重量的測量概念，由此可見 學生對重量的操作型定義較不熟悉，因此人 不受地板支持所以失重對學生的說服力較 低。亦即學生以「重量就是重力」，而鮮少使 用「物體壓在另一物體(如磅秤)的力」來解 釋失重問題，這可能與國小高年級以後的教 學強調「重量就是重力」有關。 (三) 學生以漂浮來解釋失重 說服力平均排第二的失重理由是：「失 重時重力變小所以漂起來。(b111)」，這也 反映在「失重時會飄浮，表示人所受的外力 和力為零。(b203)」，甚至連正確作答的學 生對其評分也偏高(平均約 2.4)，這可能是來 自漂浮的物體重量輕的直觀，以及從媒體或 教學得到物體失重時會飄浮的印象，而推論 物體重量變輕，所以重力變小。 (四) 學生習慣以電梯下墜的類比來考量失 重 就失重時機而言最認同的解釋是遊樂場 的 自 由 落 體 (b210) 以 及 失 速 下 墜 的 電 梯 (b201)，由此可見學生是以下墜的類比來考 量失重時機，而不習慣以何時人對飛機的相 對加速度為零(b205)來決定是否失重。 值得注意的是約半數學生未能察覺，當 飛機越過反曲點繼續下落這段時間，飛機必 須有向上加速度，使得飛機向下的鉛直速度 越來越小(b203)，亦即學生無法理解在 D 段 飛機的加速度必須向上，只是一味認為下墜 就失重。 上述討論顯示：學生在解決失重問題時 最常用遊樂場的自由落體或下墜的電梯作類 比，而以圓周運動(b105、b206) 的類比或以 拋體運動(b110、b205) 來解釋的說服力均不 高，這可能是因為教師及教科書均只以下墜 的電梯來解釋失重，使得學生對此類比較熟 悉的緣故。 (五) 提供廣度足夠的選擇理由可增加學生 的作答信心與答對率 學生自評的作答信心統計結果發現，學 生在做過理由判斷後，作答信心增加，「失重 概念」的作答信心評分從 2.92(SD1.1)增加到 3.31(SD1.02) ， 答 對 率 則 從 36.6% 增 加 至 44.6% ；「 失 重 時 機 」 的 作 答 信 心 評 分 從 3.13(SD1.22)增加到 3.48(SD1.11)，不過表面 上答對率卻降低(30.1%降至 20.5)，但是選擇 CD 的人數卻增加，可見學生受到下墜類比 的影響。 上述的結果顯示：教學時如果能提供廣 度足夠的理由，供學生判斷及選擇，有助於 提高學生的學習信心與成效，但是如果提供

的廣度不夠時，例如，只提供下墜的電梯作 類比，並無法呼應所有可能產生失重的時 機，此時雖然仍有益於學習時的信心，卻無 益於學習成效。 上述結果也提醒我們，類比可以幫助學 生學習，但是類比無法完全等同於被類比的 概念，因此說明類比的局限，或使用多重類 比(提供足夠的廣度)是有必要的。

伍、結論與建議

本研究以飛機作拋物線失重飛行來探討 高二學生的失重概念，由研究結果提出結論 與建議如下。

一、結論

根據問卷施測及晤談結果，可以得到下 列發現： (一) 學生的失重概念種類分布情形 約四成的學生知道失重並不是失去重 力，而是感受不到重量；但有三到四成的學 生認為失重就是所受重力變小；約有一成學 生認為失重就是所受重力為零；另約一成的 學生認為失重時所受重力變大。 (二) 學生的失重心智模式 以學生在問卷作答及晤談時提出的解 釋，其失重心智模式可以歸納成下列七種： 1.測量說： 所受重力沒變，而測得重量為零，因為 物體沒有受到支撐力。本項為科學模式。 2.離心力說： 離心力與所受重力平衡，所以失重。例 如學生以圓周運動的離心力與向心力作類 比。又如牛頓雜誌將重力定義為地球引力與 離心力之和，不過這可能更誤導學生對重力 與重量的理解。 3.漂浮說： 失重時人會漂浮，表示重量變輕，亦即 重力變小。這項模式來自於漂浮的物體較輕 的直觀。 4.高度說： 重力大小與距離平方成反比，越高越容 易失重，所以失重時所受重力變小；也有認 為下墜時會失重，距離地心變近，所以所受 重力變大。這類學生應用學到的萬有引力公 式，但卻未能真正了解其數量級大小的比較。 5.大氣說： 真空時無重力，有大氣就有重力，如果 失重時在大氣層內就仍受到重力。這類學生 延續了從小建構的迷思概念，這個迷思概念 可能被太空人在軌道飛行時經歷失重狀態的 現象而被加強，因為太空是真空，太空人飄 浮表示沒有重量，所以不受重力 6.零重力說： 失重就是無重量，就是無重力。 7.直覺說： 學生無法說明理由，而以直覺做判斷。 從第二至六項模式可以看出學生的失重 心智模式並未區別重力與重量，而是融合了 重量與重力的概念，目前的教學正加強了「重 力即重量」或「重量即重力的大小」的概念。 (三) 學生的失重概念受到直觀、世俗及學校 科學的影響，而建構出科學概念與另有概念 共存的個人概念 從學生對理由說服力的評分得知，學生 雖然可以接受老師教授的科學概念(第一題 的理由 b107 及 b108、第二題的理由 b205， 平均說服力大於 2.5)，不過並非全盤複製老 師教授的概念，而是在自己原有的概念及經 驗上，融合或擷取科學概念來建構屬於自己 的概念，亦即學生融合了直觀、世俗及學校 科學，而形成科學概念與另有概念，甚至相 互矛盾的概念共存的個人概念。

二、建議

從學生對「失重問卷」的各項理由評分 可以看出，如果教學能從學生的直觀及世俗 科學著手，學生就比較容易被說服。根據上 述討論及研究結果，提出下列建議： (一)區別重力與重量的定義 「物體所受的重力就是重量」這樣的重 量定義是否有必要(Figueiredo, 2005)，值得斟 酌[見圖 1(a)及(b)]。因為重力就是重量，使 得「物體所受的地球引力」這個物理量有兩 個名稱；而重量這個名稱卻有兩個不同的意 義，一個指的是接觸力的重量，另一個指的 是超距力的重力，一個名詞卻有兩個意義， 使得「重量」意義混淆不清！從本研究結果 發現重量的重力定義可能導致或強化失重的 迷思概念，而重量的操作型定義有助於學生 理解失重概念，因此建議接受某些物理學者 的意見(如， Figueiredo, 2008; Galili, 1995, 2001； King, 1962)，不要使用重量就是重力 的定義，而直接採用重量的操作型定義，而 教師在教學時要特別釐清這兩種定義。 (二)將重量視為接觸力，重力為超距力 將重量定義為作用於其支持物體的力， 是接觸力，而重力則為地球施於物體的引 力，是超距力。這樣的定義符合學生的概念 發展，對於超距力與接觸力的區分也符合學 生的直觀（見圖 1），也解決了目前教科書上 的重量與重力概念的矛盾與混淆不清。 (三)不要只以類比來預測結果，應該分析真 正原因 教師以類比做解釋時，不能只以類比來 預測結果，例如以遊樂場的自由落體來解釋 失重時，還是應該分析失重的原因，並且應 該區別類比與實際問題(如失重飛行)的區 別，避免學生誤認失重只發生在自由下落 時，必要時應該提供多重類比，例如以雲霄 飛車來類比。

參考文獻

1. 王俊貴 (2002)。國中學生力的概念學習狀 況分析研究與建議。國立高雄師範大學物 理學系碩士論文，未出版。 2. 余秀麗、譚克平(2005)。國三學生的重力 初始概念。科學教育學刊, 13(4), 413-439。 3. 林明良，陳忠志（2002，12 月）。高雄 區高中學生幾何光學另有概念之研究。論 文發表於中華民國科學教育學會、國立彰 化師範大學科學教育研究所聯合主辦之 「第十八屆中華民國科學教育學術研討 會」，彰化。 4. 林明瑞(主編)(2008)。普通高級中學基礎 物理。台南市：南一書局。 5. 林明瑞(主編)(2004)。高級中學物質科學 物理篇(上冊)。台南市：南一書局。 6. 姚如芬、林佳穎(2003)。「學校本位」數學 教學模組織發展與實踐—以國小四年級 「重量」單元為例。科學教育學刊, 11(3), 257-275。 7. 姚珩(主編)(2008)。普通高級中學基礎物 理。台南市：翰林出版。 8. 張月霞 (2005)。國小學童對地心引力概念 之認識研究。國立屏東師範學院數理研究 所碩士論文，未出版。 9. 教育部 (2003)。92 年國民中小學九年一 貫課程綱要。2008 年 10 月 20 日取自 http://www.edu.tw/EJE/content.aspx?site_c ontent_sn=4420 10.淺島誠、古川義純、山岸明彥(2008)。希 望號在太空中的任務是什麼(饒志民， 譯)。Newton 量子科學雜誌, 10, 70-75。 11.莊麗娟(2007)。三-六歲幼兒對重量概念的 認知：基礎認知與現象推理。科學教育學

刊 15(1), 73-97。 12.郭重吉、吳武雄 (1990)。利用晤談方式探 查國中學生重要物理概念的另有架構之 研究(2)。(國科會專題研究計畫成果報 告，計畫編號：NSC-79-0111-S-018-03-D) 13.郭重吉(2005)。科學概念學習資料庫緒 論 。 2009 年 6 月 29 日 取 自 http://www.sec.ntnu.edu.tw/SLS/SLS_002.h tm 14.陳文典(主編)(2007)。普通高級中學基礎 物理。台北縣：泰宇出版. 15.彭淮棟(編譯)(2007, 4 月 27 日)。殘障物理 學家霍金體驗零重力飛行。聯合晚報。 2007 年 4 月 29 日 取 自 http://mag.udn.com/mag/world/storypage.js p?f_ART_ID=65040 16. 楊宗哲 ( 主編 )(2006) 。高級 中學 基礎物 理。台北縣：全華圖書。 17.廖婉君 (2002)。國民小學中年級兒童對重 量概念認知之研究。國立台北師範學院數 理教育研究所碩士論文，未出版。 18.蔡嘉興 (2007)。從量子哲學觀探討概念理 解本質之研究：以國三學生電流概念為 例。國立高雄師範大學科學教育研究所博 士論文，未出版，高雄。 19.鄧美貴(主編)(2004)。國中自然與生活科 技(第三冊)。台北縣：康軒文教。 20.德三等人(2006)。基礎物理。台北縣：龍 騰文化。

21.Ahlgren, A. (1969, Feb.). Reliability, predictive validity, and personality bias of confidence-weighted scores. Paper presented at the American Educational Research Association Convention, Los Angeles, CA.

22.BBC (2007, April 27). Hawking takes zero-gravity flight. BBC News. Retrieved October 22, 2008, from

http://news.bbc.co.uk/2/hi/science/nature/65 94821.stm

23.Chen, C.C., Lin, H.S., & Lin, M.L. (2002). Developing a Two-Tier Diagnostic Instrument to Assess High School Students’ Understanding − The Formation of Images by a Plane Mirror. Proceeding of National Science Council, ROC, Part D, 12(3), 106-121.

24.Claxton, G. (1996). Minitheories: a preliminary model for learning science. In P.J. Black & A.M. Lucas (Eds.), Children’s informal ideas in science (pp. 45-61). London: Routledge.

25.diSessa, A.A. (1993). Toward an epistemology of Physics. Cognition and Instruction, 10(2 & 3), 105-225.

26.Echternacht, G. (1971). The use of confidence testing in objective tests. (Report No. RB-71-41). Princeton, NJ: Educational Testing Service. (ERIC Document Reproduction Service No. ED058307)

27.Figueiredo, J.M.L. (2005). Do we really need the weight force? arXiv:physics. Retrieved August 17, 2008, from

http://xxx.tau.ac.il/PS_cache/physics/pdf/05 06/0506100v5.pdf

28.Figueiredo, J.M.L. (2008). Advantages of adopting the operational definition of weight. arXiv:physics. Retrieved August 27, 2008, from

http://arxiv.org/PS_cache/physics/pdf/0505/ 0505193v5.pdf

29.Galili, I. (1993). Weight and gravity: teachers’ ambiguity and students’ confusion about the concepts. International Journal of Science Education, 14(1), 63-81.

30.Galili, I. (1995). Interpretation of students’ understanding of the concept of weightlessness. Research in Science Education, 25(1), 51-74.

31.Galili, I., & Bar, V. (1997). Children’s operational knowledge about weight. International Journal of Science Education, 19, 317-340.

32.Galili, I. (2001). Weight versus gravitational force: historical and educational perspectives. International Journal of Science Education, 23(10), 1073-1093.

33.Galili, I & Lehavi, Y. (2003). The importance of weightlessness and tides in teaching gravitation. American Journal of Physics, 71(11), 1127-1135.

34.Garvin, A.D. (1972, April). Confidence weighting. Paper presented at the annual meeting of the American Educational Research Association, Chicago, IL.

35.Gay, L.R. (1992). Educational Research Competencies for Analysis and Application. New York: MacMillan.

36.Gilbert, J.K., Osborne, R.J., & Fensham, P.J. (1982). Children’s science and its consequences for teaching. Science Education, 66(4), 623-633.

37.Gürel, Z. & Acar, H. (2003). Research into students’ view about basic physics principles in a weightless environment. Astronomy Education Review, 2(1), 65-81. 38.Hestenes, D., Wells, M., & Swackhamer G.

(1992). Force concept inventory. The Physics Teacher, 30(3), 141-158.

39.Kaaltakçi, D., & Didiş, N. (2007). Identification of pre-service Physics

teachers’ misconceptions on gravity concepts: A study with a three-tier misconception test. AIP Conference Proceedings, 899(1), 499–500.

40.Kikas, E. & Hannust, T. (2002). The influence of experimental teaching on 5- and 7-year old children’s concepts of the Earth and gravity. Journal of Baltic Science Education, 2, 19-30.

41.King A.L. (1962). Weight and Weightlessness. American Journal of Physics, 30(4), 387.

42.Kjærnsli, M., Angell, C., & Lie, S. (2002). Exploring population 2 students’ ideas about science. In D.F. Robitaille & A.E. Beaton (Eds.), Secondary analysis of the TIMSS data (pp. 127-144), Netherlands: Kluwer Academic Publishers.

43.Marion, J.B. & Hornyak, W.F. (1985). General Physics with Bioscience Essays. New York: John Wiley & Sons.

44.Needham, A. & Baillargeon, R. (1993). Intuitions about support in 4 1/2 month old infants. Cognition, 47(2), 121-148.

45.National Research Council (2005). How Students Learn: History, Mathematics, and Science in the Classroom. Committee on How People Learn. Donovan, M.S. & Bransford, J.D. (2005). Introduction. In M.S. Donovan & Bransford J.D. (Eds.). Division of Behavioral and Social Sciences and Education. Washington, DC: National Academics Press.

46.Noce, G., Torosantucci, G, & Vicentini, M. (1988). The floating of objects on the Moon: prediction from a theory or experimental facts? European Journal of Science

Education, 10(1), 61-70.

47.Osborne, R.J. and Wittrock, M. (1985). The generative learning model and its implications for science eduction. Studies in Science Education, 12, 59-87.

48.Palmer, D. (2001). Students’ alternative conceptions and scientifically acceptable conceptions about gravity. International Journal of Science Education, 23(7), 691-706.

49.Pugh, R.C. & Brunza, J.J. (1975). Effects of a Confidence Weighted Scoring System on Measures of Test Reliability and Validity. Educational and Psychological Measurement, 35( ), 73-78.

50.Serway, A. (1996). Physics for Scientists and Engineers with Modern Physics. Philadelphia, CA: Saunders College Publishing.

51.Sharp, J.G. & Sharp, J.C. (2007). Beyond shape and gravity: children’s ideas about the Earth in space reconsidered. Research Papers in Education, 22(3), 363-401.

52.Stankov, L., & Crawford, J. D. (1997). Self-confidence and performance on test of cognitive abilities. Intelligence, 25(2), 93–109.

53.Taylor, K. (1974). Weight and centrifugal force. Physics Education, 9, 357-360.

54.Treagust, D.F. (1986). Evaluating students’ misconceptions by means of diagnostic multiple choice items. Research in Science Education, 16, 199-207.

55.Treagust D.F. (1988). Development and use of diagnostic tests to evaluate students’ misconceptions in science. International Journal of Science Education, 10(2),

159-169.

56.Treagust, D.F. & Smith, C.L. (1989). Secondary students understanding of gravity and the motions of planets. School Science and Math, 89(5), 380-391.

57.Tsai, C. C., & Chou, C. (2002). Diagnosing students’ alternative conceptions in science. Journal of Computer Assisted Learning, 18, 157–165.

58.Tsai, C.H., Chen, H.Y., Chou, C.Y., & Lain, K.D. (2007). Current as the key concept of Taiwanese students understanding on electric circuits. International Journal of Science Education, 29(4), 483-496.

59.Tsai, C.H., Chen, H.Y., & Chou, C.Y. (2006, Nov.) What does it diagnose?: the alternative conceptions on the diagnosis of students’ conceptual understanding. Paper presented at 1st International Conference on SENS, Seoul.

60.Tytler, R. (2000). A comparison of year 1 and year 6 students’ conceptions of evaporation and condensation: dimensions of conceptual progression. International Journal of Science Education, 22(5), 447-468.

附錄 失重概念問卷(後測用)

新 聞 報 導 天 文 物 理 學 家 霍 金 在 2007/4/26 日 脫 離 輪 椅 自 由 自 在 飄 浮 了 八 次，每次約三十秒，共享受了四分鐘的失重 狀態。 失重狀態是由波音七二七噴射客機在 大西洋上空八千五百公尺到六千公尺間做 「拋物線」波浪狀飛行所產生。也就是飛機 飛行路線由數個向下開口和向上開口的拋物 線所組成(如圖)。請回答下列關於這則新聞的問題： 第一題： 1-0.請判斷下列敘述是否正確，不正確給 0，正確者請評定其協助作你答 1-1 的重要性或說服力。 正確(請判斷說服力) b1 錯 誤 低 普通 高 01.失重表示失去重量，所以飛機艙內的人所受重力為零。 0 1 2 3 4 5 02.失重時人會漂浮，表示人未受到重力的作用。 0 1 2 3 4 5 03.失重時人會漂浮，表示人所受的外力合力為零。 0 1 2 3 4 5 03P.飛機在最高點失重時，這時鉛直方向的速度為零，表示不受力。 0 1 2 3 4 5 04.飛機在最高點失重時，這時鉛直方向加速度為零，表示不受力。 0 1 2 3 4 5 05.像太空梭繞地球飛行，此時重力正好當作向心力，而呈失重狀 態，如太空漫步的太空人，其實他跟太空梭一起往下掉，只是 下降的幅度正好等於地球的弧度變化。 0 1 2 3 4 5 06.因為飛機和人都還在地球重力場中，而且距離地心幾乎不變(可 忽略)，所以受有重力且大小與失重前相當。 0 1 2 3 4 5 07.失重並不是真的零重力，也不是外力合力為零，而是仍受重力 作用，但在自由落下這段時間內，人和地板也以相同的重力加 速度在往下掉，因此感受不到重力。 0 1 2 3 4 5 08.失重前人感受到飛機地板的支撐，所以有重量，當飛機引擎不 再加速，此時飛機和人都只受到向下的重力加速度 g 的作用， 人相對於飛機的加速度為零，地板不需要再支撐人，所以人感 覺失重。 0 1 2 3 4 5 09.飛機有水平的向前加速度，所以在飛機上人會感受到向後的加 速度，也就是向後的力，加上原來向下的重力加速度產生的重 力，兩力的合力就是人感受的重力。 0 1 2 3 4 5 10.飛機作拋物線飛行，表示飛機在水平方向是等速運動，就像只 受重力作用的拋體運動一樣，飛機和人都受重力作用。 0 1 2 3 4 5 11.飛機並非在真正的無重力環境(如無重力場的外太空)，而是製造 出無重力狀態，因此所受重力要比失重前小才浮得起來。 0 1 2 3 4 5

1-1. ( )在波音七二七做拋物線失重飛行時，所謂的失重狀態，是真的所受重力為零嗎？ A. 飛機艙內的人所受重力為零。 B. 飛機艙內的人所受重力與失重前相同。 C. 飛機艙內的人所受重力比失重前大。 D. 飛機艙內的人所受重力比失重前小。 E. 其它(請寫下來)________________________________________________________ 第二題： 2-0.請判斷下列敘述是否正確，不正確給 0，正確者請評定其協助作你答 2-1 的重要性或說服力。 2-1.( )請看上頁圖，你認為在哪些(或哪一)段飛行時間中，可以體驗到失重狀態？ 低 高 我對 1-1 的作答信心為(請圈起來)： 1 2 3 4 5 正確(請判斷說服力) b2 錯 誤 低 普通 高 01.在 C 時飛機掉下來，只有向下的重力加速度，類似電梯失速下 墜，人會覺得失重。 0 1 2 3 4 5 02.在 D 時，飛機往下的加速度正好等於 g 值，此時才會有失重感 覺。 0 1 2 3 4 5 03.在 D 時，飛機的加速度向上，也就是飛機的鉛直速度要越來越 小。 0 1 2 3 4 5 04.在 D 斜率最大，表示加速度大小最大，而且斜率為負值，表示 飛機向下加速，所以產生失重狀態。 0 1 2 3 4 5 05.在 B 和 C 時，從向下開口的飛行拋物線軌跡得知，此時飛機作 只有向下加速度，沒有水平加速度的拋體運動，此時飛機和人 的加速度都是 g，所以飛機和人以相同的加速度上升後下降，人 對飛機的相對加速度為零，形成失重。 0 1 2 3 4 5 06.在 B 和 C 兩段，類似以地心為中心的圓周運動，此時所受的重 力作為向心力，就像繞地球作太空漫步的太空人處在失重狀態。 0 1 2 3 4 5 07.在 BCE 能體會失重，因為這三段是飛機迅速改變方向的段落， 因人體仍有原方向的切線速度，但飛機卻向另一方向，故可達 失重。 0 1 2 3 4 5 08.飛機一直有水平加速度，所以不管垂直方向加速度如何改變， 都不可能體驗失重狀態。 0 1 2 3 4 5 09.只有飛機在最高點時，鉛直速度為零，此時才是失重狀態。 0 1 2 3 4 5 10.像六福村的大怒神一樣，在自由落下的過程中體驗失重。 0 1 2 3 4 5 11.像坐在雲霄飛車，在到達頂端前後那段可以體驗失重。 0 1 2 3 4 5 低 高 我對 2-1 的作答信心為(請圈起來)： 1 2 3 4 5

A Study on the Weightlessness Concepts of Senior High School

Students

Ming-Laing Lin 1 Ming-Jun Su 2 Shing-Ho Chiang 1

1

National Kaohsiung Normal University 2

Shu-Te University

Abstract

A person standing on a scale in a free-falling elevator is weightless because the scale reading is zero. According to the gravitational definition of weight adopted by common textbooks, the weight is considered a gravity force and zero weights imply no gravity force exerted on the person. But is there really no gravity force? The purpose of this study was to explore the concepts of weightlessness that senior high school students possessed after the instruction using gravitational definition of weight. The participants were 96 eleven-graders enrolled in physics classes and completed mechanics course including the concept of weightlessness in a public high school. A survey was involved primarily and interviews were conducted with students as well. The instruments used in this study including pretest and posttest four-tier (fact-confidence-reason-confidence/persuasiveness) questionnaires concerning weightlessness concepts were developed, based on the news report about Dr. Stephen Hawking's weightless flight. Either in the pretest or posttest questionnaire, the fact-tier question is multiple-choice used to measure content knowledge, and the confidence-weighting tier is used to measure the strength of respondent’s conceptual understanding. However, the reason-tier questions in the pretest questionnaire are open-ended while they consist of some reason items with 6-point likert Scale (0=incorrect, 1=lowest persuasive, 5=highest persuasive) that designed to rate the persuasiveness of the item instead of confidence-weighting in the posttest questionnaire. The results showed that about 40% of students could perceive that the weight is zero and the gravity force does not change in the weightless situation. Only 8.5% also succeeded in answering when the passenger experiences weightlessness during a weightless flight. Students’ cognitive models of weightlessness were classified into seven categories: there were Measure Model, Centrifuge Force Model, Float Model, Altitude Model, Atmosphere Model, No-gravity Model, and Intuition Model. The gravitational definition of weight may result the inaccurate inference of “no weight, no gravity”. Teachers should distinguish “weight” of an object as a contact force exerted on its support and “gravity” as a non-contact force exerted on the object by the Earth.