Call Performance for a PCS Network
Yuguang Fang,
Student Member, IEEE, Imrich Chlamtac,
Fellow, IEEE, and Yi-Bing Lin,
Senior Member, IEEEAbstract— It is well known that, due to the mobility of a portable and limited channel availability, calls of portables may not be completed due to being blocked or terminated during the call initiation or the handover process. The characteristics of the call-completion and call-holding times for both a complete call and an incomplete call are of critical importance for establishing the actual billing process in the PCS network. In this paper, we derive the call-completion probability (hence, call-dropping probability) and the effective call-holding time distributions for complete/incomplete calls with a general cell-residence time and a general call-holding time are analyzed, and general computable formulas are obtained. We show that when call-holding times are Erlang distributed, easy-to-compute formulas for the probability of a call completion and the expected effective call-holding times for both a complete call and an incomplete call can be derived.
Index Terms—Call blocking, call-holding time, call pricing, cell residence, PCS.
I. INTRODUCTION
A
personal communications services (PCS) network allows users to communicate as they move [2], [8], [10], [17], [18]. In this network, a large number of customers can be served using spectrally efficient cellular systems [10], [18]. In this system, the service area is populated with base stations. The coverage area of a base station is called a cell. The users (the mobile phone or mobile computer) in a cell communicate via radio links to base stations. When a new call is originated and attempted in a cell, one of the channels assigned to the base station is used for the communication between the mobile portable and the base station as long as a channel is available. When all channels in a cell are in use while a new call (or handover call) is attempted in the cell, the call will be blocked and cleared from the system. When a call gets a channel, it will keep the channel until its completion, or until the mobile moves out of the cell, in which case the channel will be released for other use. When the mobile moves into a new cell while its call is ongoing, a new channel needs to be acquired in the new cell for further communication, using a handover procedure. During handover, if there is no channel available in the new cell for the “ongoing” call, it is forced to terminate before its completion [8], [10]. In order toManuscript received September 12, 1996; revised April 21, 1997. This work was sponsored in part by the Army Research Office under Grants DAAH04-96-1-0308 and DAAH04-95-1-0443.
Y. Fang is with the Department of Electrical and Computer Engineering, Boston University, Boston, MA 02215 USA.
I. Chlamtac is with the Erik Jonsson School of Engineering and Computer Science, University of Texas at Dallas, Richardson, TX 75083-0688 USA.
Y.-B. Lin is with the Department of Computer Sciences and Information Engineering, National Chiao Tung University, Hsinchu, Taiwan, R.O.C.
Publisher Item Identifier S 0733-8716(97)06095-2.
evaluate this behavior in a PCS network, the following three possibilities need to be considered.
• The call is blocked at its call initiation, and is never connected (a blocked new call).
• The call is connected, successfully makes one or more handovers, but is forced to terminate before its completion because of the lack of an available channel (an incomplete call).
• The call is connected and completed (a complete call). In a PCS system, one ideally wishes to allow all calls to be completed. Clearly, in the presence of channel availability limitations, this objective is not obtainable at all times. As an alternative, one wishes to make the call completion probability as high as the grade of service (GoS) needed.
When defining the right objective, a major practical consid-eration is obviously pricing. The use of the same flat rate for both complete and incomplete calls is unfair and commercially unattractive. To stay competitive, a PCS network provider may apply discounts for calls that were not completed [12]. However, since incomplete calls may spend significant time using PCS network resources, it is also impossible for the provider to apply a constant discount rate to all incomplete calls. In order to determine a reasonable (if not optimal) discount factor, it is therefore necessary to know for how long a call (either complete or incomplete) has used the network. The duration of the requested call connection is referred to as the call-holding time. The duration of an actual call connection for an incomplete call will be called the effective call-holding time of an incomplete call, while the duration of an actual call connection of a complete call will be called the effective call-holding time of a complete call. It is obvious that the duration of a requested call does not depend on the PCS network; it only depends on the mobile user (how long he wishes to maintain the call). For simplicity, we will term this duration the call-holding time, as this is consistent with the ideal case when there are infinite numbers of channels and the handover procedure does not affect the duration of a connection. In reality, the number of radio channels is limited, and the handover procedure does come into play. The duration of an actual call connection will depend on the PCS network: its traffic situation, channel availability, etc.
The performance modeling of a PCS network can be con-ducted at two levels. The first-level modeling uses the number of radio channels in cells as an input parameter to de-termine the new call-blocking probability and the forced termination probability. The second-level modeling uses the new call-blocking and the forced termination probabilities as input parameters to study the call-completion probability (or
the probability that a call is successfully complete) and the expected effective call-holding times of a complete or an incomplete call. This paper deals with second-level model-ing. The extension of our results to the first-level modeling is possible, and will be treated in a separate paper. Since existing cellular systems are typically engineered at 1–2% new call-blocking and forced termination, these default values may be used as the reference input parameters for second-level modeling. However, the call-completion probability and the expected effective call-holding times cannot be derived directly from these two parameters. Both the cell-residence time and the call-holding time distributions must carefully be chosen to reflect the real systems. In our model, a general cell-residence time distribution is considered, which can be used to accommodate any real PCS system. The selection of the call-holding times was in the past typically assumed to be ex-ponentially distributed. Such an assumption may be reasonable when the calls are charged based on the lengths of the call-holding times. The assumption is no longer valid, however, for the modern telephone services which apply flat-rate billing programs. Flat-rate billing encourages people to make long calls (for example, people may log on from their PC’s at home to main computers in the companies through local telephone calls, and sometimes keep the connections for several days). Thus, with current communication environments, long tails are observed for the call-holding time distributions. In recent telephone network engineering [1], lognormal distributions [5] have been used to approximate the wireline call-holding times. For most existing cellular systems, the wireless calls are charged based on the call-holding times, and these systems can be appropriately modeled with the exponential call-holding time distribution [13], [14]. However, for future PCS systems (especially the low-power PCS systems such as CT-2 [19], DECT [3], or PACS [16]), flat-rate billing programs have been proposed. Thus, it is very important that we follow the wireline telephone network engineering approach, that is, use a more general distribution to represent the call-holding time distribution.
In order to determine the call-completion probability and the effective call-holding times, we need to know the call-arrival distribution, call-holding time distribution, and cell-residence time (i.e., a mobile stays in a cell) (reflecting the frequency of handovers or the mobility of a mobile portable). We will call the duration of a call in a given cell the cell-residence time. In this paper, we will use the following assumptions.
• The call arrivals form a Poisson process.
• The cell residence times (the intervals that a portable stays in the cells) are independent, identically distributed (i.i.d.) with nonlattice distribution.
• The call-holding times are i.i.d. with nonlattice distribu-tion.
The last two assumptions are a generalization of conven-tional analysis assumptions (e.g., the commonly used expo-nential distribution satisfies these two assumptions), and are chosen to fit the emerging PCS networks. The cell-residence times should be general since the time the mobile may spend
in a cell may be highly variable due to the mobile speed and motion and the geographic situation in the cell. For example, in an urban area, the routes the mobile users take may be highly irregular. The rate of the residence times is used to describe the mobility of the mobile portable.
In the traffic models studied in the literature, the call-holding times are assumed to be exponentially distributed for reasons of tractability [6], [21]. Under the assumption of exponentially distributed call-holding times, Lin et al. [13], [14] studied the performance of channel assignment strategies, and obtained analytical results for forced termination probability and new call-blocking probability. Under the same assumption, Lin and Chlamtac [12] analyzed the call-completion probability and the expected effective call-holding times. However, as pointed out by Guerin [4], the most commonly used assumption for finding the blocking probabilities, i.e., the channel occupancy time is exponentially distributed, may not be valid for some cellular networks. The reason for this is that either the call-holding times or the cell-residence times are not exponentially distributed. Zonoozi et al. [22] used the generalized Gamma distributions to model the cell-residence times.
In this paper, we study the case of PCS networks using the generalized assumptions above. For this generalized model, we obtain formulas for the call-completion probability and the distribution (its Laplace transforms) of the effective call-holding times of both complete and incomplete calls, from which expected effective call-holding times can be derived. When the call-holding times are Erlang distributed, easily computable formulas are given and recursive algorithms are developed.
II. CALL-COMPLETION PROBABILITY
In this section, we study the call-completion probability. Previously, Lin and Chlamtac [12] obtained a formula for the call-completion probability for a PCS network with a general residence time distribution and exponential call-holding time distribution. Here, we generalize these results to the case when call-holding times have a more general distribution.
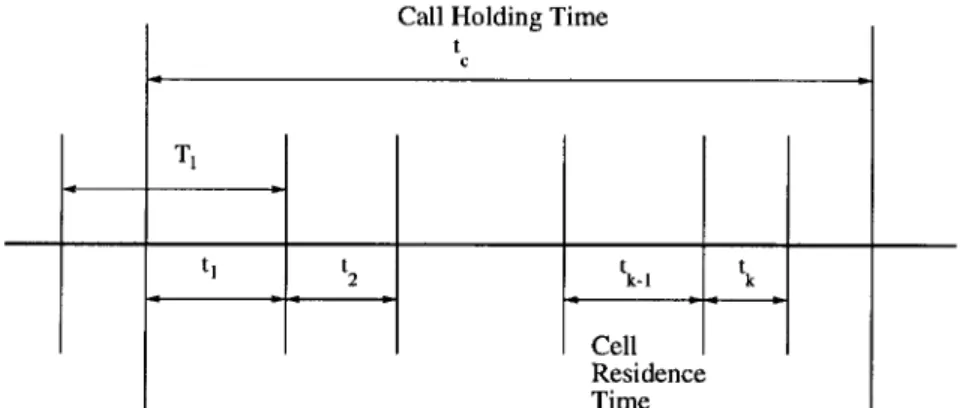
We first consider the effective call-holding time for an incomplete call. Fig. 1 illustrates the timing diagram for the call-holding time, where is the time that the portable resides at cell 1, and ( ) is the residence time at cell . According to our assumptions, are i.i.d. Let have nonlattice density function with mean and let be the Laplace transform of (we will use to denote the Laplace transform following the tradition [9]). Suppose that a call for the portable occurs when the portable is in cell 1. Let be the interval between the time instant when the call arrives and that when the portable moves out of cell 1. Let and be the density function and the Laplace transform of the distribution, respectively. From the renewal theory [9], is the residual life of the cell-residence time of the portable in cell 1, so we have
Fig. 1. Timing diagram for a forced terminated call at kth handover.
(2)
Consider the effective holding time where
and are its density function and Laplace transform. Since ( ) are i.i.d., it is easy to derive
(3) Let be the probability that a new call attempt is blocked (i.e., the call is never connected), let be the probability that a call is completed (i.e., the call is connected and completed), and let be the forced termination probability or the probability that no radio channel is available when a handoff call arrives. Then the probability of an incomplete call (i.e., the call is connected but is eventually forced to terminate)
is , which can be expressed as call is not blocked, making
handoffs and blocked at th handoff
(independency)
(4)
where is the density function of the call-holding times. In the last equation, the term in is the probability that a call is forced to terminate at the th handover (notice that the call is connected with probability , and then makes successful handovers with probability and is forced to terminate at the th handover with probability ). In the following derivation, we use the inverse Laplace transform formula. We will use to denote the real number with appropriate meaning used in the inverse Laplace transform formula [11]. From (4), we have
(5) Assume that the is such that
for any (this will be true for most interesting distributions with finite mean); then, choosing , we have
Moreover, we have
Taking this into (5), we obtain
(6) Since has no poles in the right half complex plane,
. Let denote the set of poles of
in the right half complex plane (i.e., is
the set of poles of in the left half plane). Choosing the contour that includes the vertical line and the semicircle , noticing that the integrand in (6) is on the order of as , and using the Residue theorem [11], from (6), we obtain
Res
from which, and the fact that the residue of an analytic function is zero, we finally arrive at the following.
Theorem 1: The probability that a call is completed is given by
Res (7)
where denotes the residue at pole .
Remark: Since is analytic and bounded by unity in the right half complex plane, the
is analytic in the right half plane; hence, the function has the same poles (including multiplicities) as the function in the right half complex plane. In the computation of the residue in Theorem 1, we only need to consider the poles and their corresponding multiplicities.
Next, we show how to compute for a few specific cases. If the call-holding times are exponentially distributed with density function , then its Laplace transform
is given by which has a simple pole in
the left half plane. From Theorem 1, we obtain Res
Res
(8) This is obtained in [12] using a different approach.
Assume now that the call-holding times are Erlang dis-tributed with the following density function:
where is the shape parameter and is the scale parameter. This density function has the following Laplace transform:
and has a unique pole at in the right half complex plane. Let
As we remarked before, this function is analytic in the right half complex plane. From Theorem 1, we obtain
Thus, we have the following.
Corollary 1: For a PCS network with Erlang call-holding times, the probability of a call completion is given by
(9)
where denotes the derivative of th order.
When , we have
this is the same as (8) ( in this case), which is not surprising because the Erlang distribution is exponential when
.
When , note that
Thus, from Corollary 1, we obtain
(10) It is observed that as increases, the computation becomes much more involved. We will give a recursive algorithm for the computation of which is needed in Corollary 1. Let
(11) Using the formula
(12)
we obtain
(13)
Since we have , differentiating both sides
and applying (12), we obtain ( )
From this, we obtain the following recursive algorithm to
compute :
(14) Thus, using (13) and (14), we can easily compute , and hence from Corollary 1.
III. THEEXPECTED EFFECTIVE-CALL HOLDINGTIMES
In the preceding section, we discussed the probability for a call to complete. However, this quantity does not address the time needed for a call to complete. It is desirable to know how much time is needed for a complete call to finish, and how much time an incomplete call spends using the resource (bandwidth) so that an appropriate pricing scheme can be devised. In this section, we present a solution to this problem. Similar to the argument in [12], the density function for the effective call-holding time of an incomplete call that is forced to terminate is given by
(15)
where denotes the probability of a call to be incomplete and is computed in the last section. In the first equation, the term under the summation is the density that the call is forced to terminate after handovers.
Next, we want to find the Laplace transform of from which the expected value can be easily obtained. From (15), we have
(16) Similar to the argument in the last section, we have
Taking this into (16), we obtain
(17) Note that
so is a removable singular point [11] of the integrand of (17). Thus, the poles of the integrand in the right half complex
plane are those of , i.e., . As in the
last section, we obtain the following. Theorem 2:
Res (18)
Now, assume that the call-holding times are Erlang
dis-tributed with parameter . Then .
Let
(19) Then, from Theorem 2, we have
Res
Res
(20) Finally, we arrive at the following.
Fig. 2. Timing diagram for the effective call times of a complete call: the call completes after k handovers. Theorem 3: For a PCS network with Erlang-distributed
call-holding times, the Laplace transform of the density func-tion of the effective call-holding time of an incomplete call is given by
(21)
the expected effective call-holding time of an incomplete call is given by
(22)
and the variance of the effective incomplete call-holding times is given by
(23)
Proof: Equation (22) can be obtained by noticing that . Equation (23) can be proved by the following
relationship: for any random
variable .
Remark: In fact, from (21), we can easily find all moments of the effective call-holding time of an incomplete call, which is easily given by let denote the th moment
When , the Erlang distribution is the exponential distribution. In this case, we have
and
(24) This is the same as in [12], where a different approach is used. Using (8) in (24), we obtain
Since and , we have ,
i.e., the expected effective call-holding time of an incomplete call is less than the expected noninterrupted call-holding time. For , we can also give a recursive algorithm as before to compute which is needed in (22). Let
(25) Then, we have
(26) and
(27) Thus, using (26) and (27), we can easily compute
( ), and hence from Theorem 3.
Next, we study the expected effective holding time for a complete call. The timing diagram is shown in Fig. 2, in which the call is completed when the portable is in cell . represents, as before, the effective call-holding time for a
complete call. If , , while if ,
then we have
for (28)
for
(29) Using a similar argument in [12] (or a simple conditional probability argument), we can obtain the density function of the effective call-holding time of a complete call given by
(30) where
(31)
(32)
corresponds to (28) and corresponds to (29), where is the probability of nonblocking, and
is the probability of no forced termination. Equation (30) can
be derived from where
denotes the probability that the call is completed in cell and the effective call-holding time does not exceed . Rigorous derivation can be obtained following a similar argument in [13].
We first find the Laplace transforms of and . From (31) and the Residue theorem, we have
Res
(33) Note that
where denotes the convolution operator; hence, the
Laplace transform of is
. From (32) and the Residue theorem, we have
Res
(34) From (33) and (34), we finally obtain the following.
Theorem 4: For a PCS network, the Laplace transform of the density function of the effective call-holding time of a
complete call is given by
Res
Res (35)
Suppose now that the call-holding times are Erlang distributed with parameter with Laplace transform
. Let (36) (37) Then, we have Res Res Res and Res Res
From these and Theorem 4, we obtain the following. Theorem 5: For a PCS network with Erlang-distributed call-holding times, the Laplace transform of the density func-tion of the effective call-holding time of a complete call is given by
(38) the expected effective call-holding time of a complete call is given by
(39) and the variance of the effective complete call-holding times is given by
(40)
Remark: In fact, all moments of the effective call-holding time of a complete call can be obtained from (38), and are given as follows (let denote the th moment):
When , i.e., the call-holding times are exponentially distributed, we have
This is obtained in [12] using a different approach. This formula can be further simplified using (8) as follows:
(41)
It is observed from simulation in [12] that when the cell residence times are Gamma distributed. Using this equation, we can prove this analytically for general cell-residence distribution. We want to show that the term in the last equation of (41) is nonnegative. Let
Since , . Also, we have
where we have used that , , and
. Thus, is an increasing function; hence, , from which we conclude that the term in the last equation of (41) is nonnegative. Thus, for any cell-residence distribution, the expected effective call-holding time of a complete call is always less than the expected call-holding time.
When , the closed-form formula may be quite involved. However, as before, recursive formulas can be easily
developed for the computation of and . For
, we have
(42)
For , let as defined in
(11), can be computed as in (13), and as shown in (43), found at the bottom of the page.
As observed earlier, we can analytically prove that for exponentially distributed call-holding times, the expected ef-fective call-holding times for both a complete call and an incomplete call are less than the expected call-holding time. However, it is difficult to analytically prove from the formula for that the expected effective call-holding times for both a complete and an incomplete call are less than the expected call-holding time . The following intuitive argument can be used to prove this: the effective call-holding times are just the “interrupted” call-holding times, and hence should be “smaller” than the “noninterrupted” call-holding times. We will verify this observation in the next section.
IV. ILLUSTRATIONS AND DISCUSSIONS
In this section, we present an example to show how to apply our results to analyze the effective call-holding times and attempt to draw some general conclusions. In this section, we assume that the cell-residence times are Gamma distributed
with the following density function and Laplace transform:
which have mean and variance . The
call-holding times are Erlang distributed with the following density function and Laplace transform:
which have mean and variance . We will
investigate how the probability of a call completion and the expected effective call-holding times are affected by some parameters such as the means and variances. In this section, we use the commonly used average call-holding time
min [10]; we use when we vary , while we use when we vary .
As mentioned earlier, the lognormal distributions have been proved to be a good approximation to the wireline call-holding time distribution [1]. Statistically, both the lognormal distribu-tions and Gamma distribudistribu-tions (including Erlang distribudistribu-tions) have the same capacity to approximate the measured data [7]; the assumption of Erlang call-holding times seems to be a reasonable replacement of the lognormal distributions for the performance analysis. An important advantage of the Erlang/Gamma distribution over the lognormal distribution is that the Erlang/Gamma distribution has a simple Laplace transform, which is a desired property in our modeling.
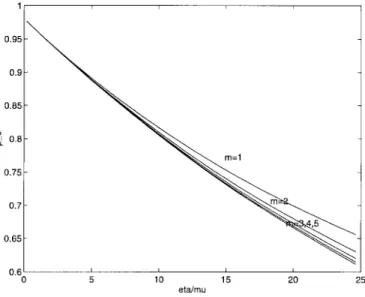
We first consider the probability of a complete call. Fig. 3 shows the probability of a call completion versus the inverse of the expected cell-residence time normalized by , i.e., the mobility , for different values of the shaping parameter in the Gamma distribution, while Fig. 4 demonstrates the variability of the call-completion probability against the mobility for various values of the shaping parameter in the Erlang distribution of the call-holding times. When is fixed, the variance of the cell-residence times (the call-holding times, respectively) is uniquely determined by the shaping parameter ( ). From Figs. 3 and 4, we can observe the following properties.
1) The call-completion probability decreases as the expected cell-residence time ( ) decreases. This is reasonable because, for a fixed mobile route, i.e., the
Fig. 3. Probability of a call completion: varying .
Fig. 4. Probability of a call completion: varyingm.
distribution of the cell-residence time is fixed, then the expected cell-residence time is fixed, and the longer the expected call-holding time, the more often the handovers happen, and the greater the chance the call will be dropped. This is equivalent to saying that for a fixed call-holding time pattern (or the fixed expected call-call-holding time), the probability of dropping the call increases as the expected cell-residence time becomes smaller; hence, the probability of a call completion decreases as the expected cell residence time increases.
2) The call-completion probability decreases as the vari-ance of the cell-residence times or the varivari-ance of the call-holding times decreases (i.e., as or increases). 3) When the expected cell-residence time is large (i.e., when is small), the effect of the variance of the call-holding times on the call-completion probability is not significant. This is why the call-completion probability alone is not a good evaluation measure for a PCS network, and the effective call-holding times are needed.
(a)
(b)
Fig. 5. Effective call-holding time of an incomplete call: varying .
4) There is a significant difference between the for and that for ; this may be due to the fact that the exponentially distributed call-holding times ( ) are memoryless.
We remind readers that the above properties hold when the new call-blocking probability and the handoff call-blocking probability are fixed (the second-level modeling); this is the situation when one is asked to compute the call-completion probability for a PCS network already in operation. Of course, call-completion probability is also dependent on some other factors such as the number of channels and carried traffic; this dependency is implied in the new call-blocking probability and . By varying the values of and , we can observe the properties of call-completion probability.
Next, we study the effective call-holding times.
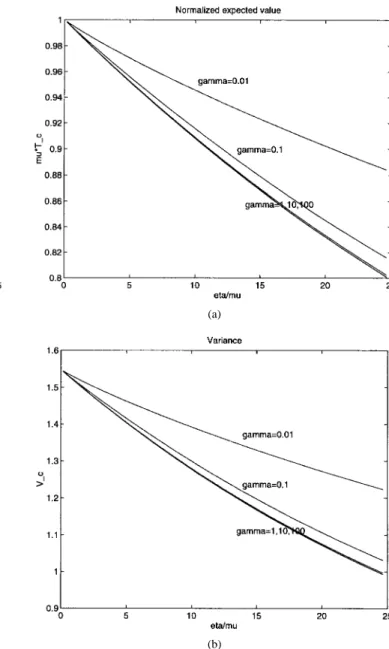
Figs. 5 and 6 show the expected effective call-holding time of an incomplete call. From these figures, we obtain the following observations for the expected effective call-holding times of an incomplete call.
(a)
(b)
Fig. 6. Effective call-holding time of an incomplete call: varyingm.
1) , i.e., . This implies that the expected effective call-holding time for an incomplete call is no more than the expected noninterrupted call-holding time, which is consistent with the observation we made based on our intuition.
2) is decreases as the mobility parameter increases. This is intuitive because when increases, the cell-residence times decrease, more handovers are undertaken, more often the call is incomplete, and hence the incomplete call-holding times tend to be shorter.
3) For small mobility , the expected incomplete call-holding time decreases as the variance of the cell resi-dence times increases, while for large mobility , this is reversed.
4) decreases as the variance of the call-holding times decreases for a longer range of mobility. This relation-ship will be expected to reverse for very large mobility (which may be an impractical range).
(a)
(b)
Fig. 7. Effective call-holding time of a complete call: varying .
5) There is a big difference between the case for (the exponential distribution case) and the case for , which may be contributed from the memoryless property of the exponential distribution.
6) The variance of the effective call-holding time of an incomplete call decreases as the mobility increases; for small mobility , it increases as the variance of the cell-residence times decreases, however, for large mobility , it decreases as the variance of cell-residence times decreases. It always decreases as the variance of the call-holding times decreases.
Finally, we observe the expected effective call-holding time of a complete call.
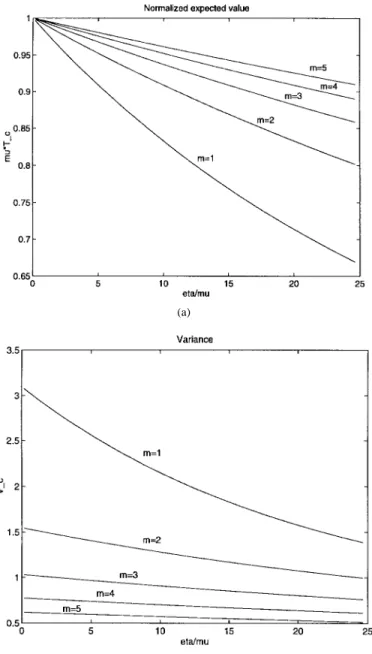
Figs. 7 and 8 show the results for the effective complete call-holding times. We have the following observations.
1) , i.e., . This implies that the expected effective call-holding time for a complete call is no more than the expected noninterrupted call-holding time,
(a)
(b)
Fig. 8. Effective call-holding time of a complete call: varyingm.
which is consistent with the observation we made based on our intuition.
2) decreases as the mobility increases. This is not intuitive.
3) The expected effective complete call-holding time decreases as the variance of the cell-residence times decreases.
4) increases as the variance of the call-holding times decreases.
5) There is a major difference between the case for (the exponential distribution case) and the case for
, which may be contributed from the memoryless property of the exponential distribution.
6) The variance of the effective call-holding times always decreases as the mobility increases; it always de-creases as the variance of cell-residence times dede-creases; and it always decreases as the variance of call-holding times decreases.
As mentioned in the Introduction, the study of the effective call-holding times can support the provider’s billing activity. Lin and Chlamtac [12] investigated the billing problem for the case when call-holding times are exponentially distributed. Similar conclusions can be drawn for our cases here. For details of this application of our results to pricing strategies, the interested reader is referred to [12].
V. CONCLUSIONS
All previous performance studies of PCS channel alloca-tion assumed that the call-holding times are exponentially distributed. While this assumption can be justified for ex-isting cellular systems where the wireless calls are charged based on the lengths of the call-holding times, future PCS systems may exercise flat-rate billing programs, and therefore a more general distribution is necessary for modeling the call-holding times. In this paper, we use a general distribution to model the call-holding times, and derive general formulas for the probability of a call completion and the expected effective call-holding times of both complete and incom-plete calls. By specifying the call-holding time distribution to be Erlang, we obtain easy-to-compute recursive formulas to compute the above performance metrics. Our results can be directly applied to pricing strategies for the emerging PCS networks.
REFERENCES [1] Bellcore, private communications, 1995.
[2] D. C. Cox, “Wireless personal communications: What is it?,” IEEE
Personal Commun. Mag., pp. 20–35, Apr. 1995.
[3] ETSI, Digital European Telecommunications Services and Facilities
Requirements Specification, Tech. Rep. ETSI, DI/RES 3002, European
Telecommunications Standards Institute, 1991.
[4] R. A. Guerin, “Channel occupancy time distribution in a cellular radio system,” IEEE Trans. Veh. Technol., vol. VT-35, no. 3, pp. 89–99, 1987.
[5] N. A. J. Hastings and J. B. Peacock, Statistical Distributions. New York: Wiley, 1975.
[6] D. Hong and S. S. Rappaport, “Traffic model and performance analysis for cellular mobile radio telephone systems with prioritized and non-prioritized handoff procedures,” IEEE Trans. Veh. Technol., vol. VT-35, no. 3, pp. 77–92, 1986.
[7] N. L. Johnson, Continuous Univariate Distributions, Vol. 1. New York: Wiley, 1970.
[8] I. Katzela and M. Naghshineh, “Channel assignment schemes for cellular mobile telecommunication systems: A comprehensive survey,” IEEE
Personal Commun., vol. 3, pp. 10–31, June 1996.
[9] L. Kleinrock, Queueing Systems: Theory, Volume I. New York: Wiley, 1975.
[10] W. C. Y. Lee, Mobile Cellular Telecommunications: Analog and Digital
Systems, 2nd ed. New York: McGraw-Hill, 1995.
[11] W. R. LePage, Complex Variables and the Laplace Transform for
Engineers. New York: Dover, 1980.
[12] Y. B. Lin and I. Chlamtac, “Effective call holding times for a PCS network,” IEEE J. Select. Areas Commun., submitted for publication. [13] Y. B. Lin, S. Mohan, and A. Noerpel, “Queueing priority channel
assignment strategies for handoff and initial access for a PCS network,”
IEEE Trans. Veh. Technol., vol. 43, no. 3, pp. 704–712, 1994.
[14] Y. B. Lin, A. Noerpel, and D. Harasty, “The sub-rating channel assignment strategy for PCS hand-offs,” IEEE Trans. Veh. Technol., vol. 45, Feb. 1996.
[15] S. Nanda, “Teletraffic models for urban and suburban microcells: Cell sizes and handoff rates,” IEEE Trans. Veh. Technol., vol. 42, no. 4, pp. 673–682, 1993.
[16] A. R. Noerpel, Y. B. Lin, and H. Sherry, “PACS: Personal access communications system—A tutorial,” IEEE Personal Commun., vol. 3, pp. 32–43, June 1996.
[17] J. E. Padgett, C. G. Gunther, and T. Hattori, “Overview of wireless personal communications,” IEEE Commun. Mag., pp. 28–41, Jan. 1995. [18] K. Pahlavan and A. H. Levesque, Wireless Information Networks. New
York: Wiley, 1995.
[19] R. Steedman, “The common air interface MPT 1375,” in Cordless
Telecommunications in Europe, W. H. W. Tuttlebee, Ed. New York: Springer-Verlag, 1990.
[20] S. Tekinay and B. Jabbari, “A measurement-based prioritization scheme for handovers in mobile cellular networks,” IEEE J. Select. Areas
Commun., vol. 10, no. 8, pp. 1343–1350, 1992.
[21] W. C. Wong, “Packet reservation multiple access in a metropolitan microcellular radio environment,” IEEE J. Select. Areas Commun., vol. 11, no. 6, pp. 918–925, 1993.
[22] M. M. Zonoozi, P. Dassanayke, and M. Faulkner, “Generalized gamma distribution for the cell residence time in cellular systems,” in Proc.
Aus-tralian Telecommun. Networks Appl. Conf. (ATNAC), Sydney, Australia,
Dec. 1995, pp. 407–411.
[23] , “Mobility modeling and channel holding time distribution in cel-lular mobile communication systems,” in IEEE Proc. GLOBECOM’95, Singapore, Nov. 1995, pp. 12–16.
Yuguang Fang (S’92–M’94–S’96) received the B.S. and M.S. degrees in mathematics from Qufu Normal University, Shandong, P.R.C., in 1984 and 1987, respectively, the Ph.D. degree in systems and control engineering from Case Western Reserve University, Cleveland, OH, in January 1994, and the Ph.D. degree in electrical and computer engineering from Boston University, Boston, MA, in May 1997. From 1987 to 1988, he held research and teaching positions in both the Mathematics Department and the Institute of Automation at Qufu Normal University. From 1989 to 1993, he was a Teaching and Research Assistant in the Department of Systems, Control, and Industrial Engineering at Case Western Reserve University, where he became a Research Associate from January to May 1994. He held a Postdoctoral Research Associate in the Department of Electrical and Computer Engineering at Boston University from 1994 to 1995. From 1995 to 1997, he was a Research Assistant in the Department of Electrical and Computer Engineering. His research interests include wireless networks and mobile communications, personal communications services (PCS), stochastic and adaptive systems, hybrid systems in integrated communications and controls, robust stability and control, nonlinear dynamical systems, and neural networks.
Imrich Chlamtac (M’86–SM’86–F’93) received the B.Sc. and M.Sc. degrees in mathematics awarded with highest distinction, and the Ph.D. degree in computer science from the University of Minnesota in 1979.
He is a Professor of Electrical Engineering and holds the Distinguished Chair in Tele-communications at the University of Texas at Dallas. He is also a member of the Photonics Center at Boston University, and President of BCN Inc., a company dealing with network design, integration, and technology transfer in wireless data, and high-speed communications jointly with Boston University. His research interests include research and implementation aspects of mobile networks and wireless communication systems, optical networks, ATM, and multimedia communication. He has published close to 200 papers in refereed journals and conferences. He is the author of more than 30 invited papers, multiple book chapters, and encyclopedias. In 1981, he coauthored the first textbook on LAN’s entitled, Local Networks: Motivation, Technology
and Performance.
Dr. Chlamtac serves as the founding Editor in Chief of the
ACM/URSI/Baltzer Wireless Networks (WINET) and the ACM/Baltzer Journal on Special Topics in Mobile Networks and Applications (MONET). He
served on the Editorial Boards of IEEE TRANSACTIONS ONCOMMUNICATIONS,
Computer Networks, and ISDN Systems, High Speed Networks Journal, Telecommunication Systems, and the Photonic Network Communications Journal. He was a Guest Editor for the PROCEEDINGS OF THEIEEE, the IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, IEEE TRANSACTIONS ON COMPUTERS, and other journals. He served as the General Chair of leading ACM and IEEE conferences and workshops, including ACM Sigcomm, ACM/IEEE, MOBICOM, and IEEE CCW, and acts as the ACM/IEEE MOBICOM Steering Committee Chair. He is the Chairman of ACM SIGMOBILE, the Special Interest Group on Mobile Computing and Networking. He is a Fellow of the ACM, winner of the Society of Computer Simulation Award, and ACM Best Paper Award. In the past, he was an IEEE, Northern Telecom, and BNR Distinguished Lecturer, and a plenary and keynote speaker at leading conferences. He was a Fulbright Scholar, and is an Honorary Member of the Senate at the Technical University of Budapest.
Yi-Bing Lin (S’80–M’96–SM’96) received the B.S.E.E. degree from National Cheng Kung Uni-versity in 1983, and the Ph.D. degree in computer science from the University of Washington in 1990.
From 1990 to 1995, he was with the Applied Research Area at Bell Communications Research (Bellcore), Morristown, NJ. In 1995, he was appointed as a Professor of Department of Computer Science and Information Engineering, National Chiao Lung University. In 1996, he was appointed as Deputy Director of Microelectronics and Information Systems Research Center, NCTU. His current research interests include the design and analysis of personal communications services network, mobile computing, distributed simulation, and performance modeling.
Dr. Lin is a Subject Area Editor of the Journal of Parallel and Distributed
Computing, an Associate Editor of the International Journal in Computer Simulation, an Associate Editor of IEEE NETWORKS, an Associate Editor of SIMULATION magazine, an Area Editor of ACM Mobile Computing and
Communication Review, a columnist for ACM Simulation Digest, a member
of the Editorial Board of International Journal of Communications Systems, a member of the Editorial Board of Computer Simulation Modeling and
Analysis, Program Chair for the 8th Workshop on Distributed and Parallel
Simulation, General Chair for the 9th Workshop on Distributed and Parallel Simulation, Program Chair for the 2nd International Mobile Computing Conference, the Publicity Chair of ACM SIGMOBILE, Guest Editor for the ACM/Baltzer WINET Special Issue on Personal Communications, and Guest Editor for IEEE TRANSACTIONS ONCOMPUTERSSpecial Issue on Mobile Computing.