The Circular Chromatic
Number of the Mycielskian
of
G
d
k
Lingling Huang and Gerard J. Chang∗
DEPARTMENT OF APPLIED MATHEMATICS NATIONAL CHIAO TUNG UNIVERSITY HSINCHU 30050, TAIWAN E-mail: llhuang,gjchang@math.nctu.edu.tw
Received February 2, 1998; revised November 23, 1998
Abstract: In a search for triangle-free graphs with arbitrarily large chromatic numbers, Mycielski developed a graph transformation that transforms a graphG into a new graphµ(G), we now call the Mycielskian ofG, which has the same clique number asGand whose chromatic number equalsχ(G)+1. Chang, Huang, and Zhu [G. J. Chang, L. Huang, & X. Zhu, Discrete Math, to appear] have investi-gated circular chromatic numbers of Mycielskians for several classes of graphs. In this article, we study circular chromatic numbers of Mycielskians for another class of graphsGdk. The main result is thatχc(µ(Gdk)) = χ(µ(Gdk)), which settles a prob-lem raised in [G. J. Chang, L. Huang, & X. Zhu, Discrete Math, to appear, and X. Zhu, to appear]. Asχc(Gdk) = kdandχ(Gdk) = dkde, consequently, there exist graphsG such thatχc(G)is as close toχ(G) − 1as you want, butχc(µ(G)) = χ(µ(G)).
c
1999 John Wiley & Sons, Inc. J Graph Theory 32: 63–71, 1999
Keywords: chromatic number; circular chromatic number; color; Mycielskian; triangle; clique
number
1. INTRODUCTION
In a search for triangle-free graphs with arbitrarily large chromatic numbers, Mycielski [9] developed an interesting graph transformation as follows. For graph
∗Correspondence to:Gerard J. Chang
Contract grant sponsor: National Science Council. Contract grant no.: NSC87-2115-M009-007.
c
G = (V, E) with vertex set V and edge set E, the Mycielskian of G is the graph µ(G) with vertex set V ∪ V0 ∪ {u}, where V0 = {x0 : x ∈ V }, and edge set
E ∪ {xy0 : xy ∈ E} ∪ {y0u : y0 ∈ V0}. For k ≥ 2, let µk(G) = µ(µk−1(G)).
Mycielski showed thatχ(µ(G)) = χ(G) + 1 for any graph G, and ω(µ(G)) =
ω(G) for any graph G with at least one edge. Hence, µk(K2) is a triangle-free
graph of chromatic number k + 2. Besides the interesting properties involving their chromatic numbers and cliques numbers, Mycielski’s graphs also have some other parameters that behave in a predictable way. For example, it was shown by Larsen, Propp, and Ullman [8] thatχf(µ(G)) = χf(G) +χ 1
f(G) for any graphG,
where χf(G) is the fractional chromatic number of a graph. Mycielski’s graphs were also used by Fisher [5] as examples of optimal fractional colorings that have large denominators. Many interesting properties for circular chromatic numbers of Mycielski’s graphs were proved by Chang, Huang, and Zhu [4]. Yet more questions concerning this topic remain open. In this article, we investigate circular chromatic numbers of Mycielskians of the graphsGdk, to be defined below, and settle a problem raised in [4] (also see Problem 7.22 in [12]).
The circular chromatic number of a graph is a natural generalization of the chro-matic number, introduced by Vince [10] under the name ‘‘star chrochro-matic number.’’ For a good survey, see [12]. Supposek and d are positive integers such that k ≥ 2d. A(k, d)-coloring of a graph G = (V, E) is a mapping φ from V to {0, 1, . . . , k−1} such thatd ≤ |φ(x) − φ(y)| ≤ k − d for any edge xy in E. In the definition, we callφ(x) the color of x. The circular chromatic number χc(G) of G is the infimum of the ratios kd for which there exists a(k, d)-coloring of G. Note that Vince [10] proved that the infimum is attained for somek ≤ |V (G)|.
Note that a(k, 1)-coloring of a graph G is just an ordinary k-coloring of G. It follows thatχc(G) ≤ χ(G) for any graph G. On the other hand, it has been shown [1, 10, 11] thatχ(G)−1 < χc(G). Therefore, χ(G) = dχc(G)e. However, two graphs with the same chromatic number may have different circular chromatic numbers. In some sense,χc(G) is a refinement of χ(G) and it contains more information about the graph.
It was shown [4] thatχc(µ(G)) = χ(µ(G)) for several classes of graphs G, and also χc(µ(H)) < χ(µ(H)) for some classes of graphs H. However, it seems difficult to characterize those graphs G for which χc(µ(G)) = χ(µ(G)). For two positive integersk and d such that k ≥ 2d, Gdk is the graph with vertex set
{0, 1, . . . , k − 1} in which ij is an edge if and only if d ≤ |i − j| ≤ k − d. It is
easy to see (also [1]) that a graphG is (k, d)-colorable if and only if there exists a homomorphism fromG to Gdk. Therefore, in the study of circular chromatic num-bers, the graphsGdk play the same role that complete graphsKndo in the study of chromatic numbers. It was shown in [4] thatχc(µ(Kn)) = χ(µ(Kn)) for any
n ≥ 3. We consider the analogous problem: does χc(µ(Gdk)) = χ(µ(Gdk))?
The main result of this article is to give a positive answer to the above problem. Also, since χc(Gdk) = dk and χ(Gdk) = dkde (see Vince [10]), a consequence is that there exist graphsG such that χc(G) is as close to χ(G) − 1 as you want, but
χ(µ(G)), the result shows that the circular chromatic number of a graph G does
not determine ifχc(µ(G)) = χ(µ(G)).
2. CIRCULAR CHROMATIC NUMBER OFµ(Gdk)
The main result of this article is the following.
Theorem 1. χc(µ(Gdk)) = χ(µ(Gdk)) = dkde+1 for any positive integer k > 2d. Note that fork = 2d, we have Gdk∼= dK2andµ(Gdk) is the graph obtained from
d copies of C5 by identifying one vertex in each copy. Therefore,χc(µ(Gdk)) =
2.5 < 3 = χ(µ(Gd k)).
Also, sinceχc(Gdk) = kd andχc(µ(Gdk)) = χ(µ(Gdk)) for any positive integers
k > 2d, we also have the following consequence.
Corollary 1. There exists a graphG such that χc(G) is as close to χ(G) − 1 as you want, butχc(µ(G)) = χ(µ(G)).
In the remaining of this section, we shall prove Theorem 1. The following lemma was proved in [4], which takes care of a special case of the main theorem.
Lemma 1. Ifχ(G) = 3, then χc(µ(G)) = χ(µ(G)) = 4.
For ann-coloring c : V (G) 7→ {0, 1, . . . , n − 1} of G = (V, E), we denote by
Dc(G) the directed graph with vertex set V such that there exists an arc from x to
y if and only if xy ∈ E and c(x) + 1 ≡ c(y)(modn). It was shown in [6] that an n-chromatic graph G satisfies χc(G) < n if and only if G has an n-coloring c for
whichDc(G) is acyclic. This result was refined [4] to the following lemma, which is useful for studying circular chromatic numbers of Mycielski’s graphs.
Lemma 2. If χc(µ(G)) < χ(µ(G)) = n, then there exists an n-coloring c of µ(G) such that Dc(µ(G)) is acyclic, c(u) = 1, and c(x0) 6∈ {0, 1} for all
x0 ∈ V0. Moreover, for any such coloring c, there is an edge xy ∈ E(G) such that
{c(x), c(y)} = {0, 1} and c(x0) = c(y0).
Write k = dr + i, where d ≥ 2 and 1 ≤ i ≤ d. Note that µ(Gddr+1) is a subgraph ofµ(Gddr+i). If Theorem 1 holds for the special case when i = 1, then
r + 2 ≤ χc(µ(Gddr+1)) ≤ χc(µ(Gddr+i)) ≤ χ(µ(Gddr+i)) = r + 2 and so the
general case follows. Hence, it remains to prove Theorem 1 for the special case whenk = dr + 1.
For clarity of notation, we considerGddr+1 as the graph with vertex set V =
{x0, x1, . . . , xdr} and edge set E = {xixj : d ≤ |i − j| ≤ (dr + 1) − d};
and the Mycielskianµ(Gddr+1) as the graph with vertex set V ∪ V0 ∪ {u}, where
V0 = {x0
i : xi ∈ V }, and edge set E ∪ {xix0j : xixj ∈ E} ∪ {x0ju : x0j ∈ V0}.
Indices of the verticesxiandx0iare taken modulodr+1, if arithmetic operations are performed on them. LetVi,j = {xi, xi+1, . . . , xj} and Vi,j0 = {x0i, x0i+1, . . . , x0j}. Note thatVi,jandVi,j0 are of sizej − i + 1 for i ≤ j, and of size dr + 1 + j − i + 1 fori > j.
It is known thatχc(Gddr+1) = r + 1d (see Vince [10]),χ(Gddr+1) = r + 1, and
χ(µ(Gd
dr+1)) = r + 2. We now show the case of k = dr + 1 for Theorem 1. Theorem 2. χc(µ(Gddr+1)) = χ(µ(Gddr+1)) = r + 2 for any positive integer
r ≥ 2.
Proof. Note thatGd2d+1 is, in fact, the odd cycleC2d+1. According to Lemma 1, the theorem holds forr = 2. So, we may assume that r ≥ 3. Let G = (V, E) be the graphGddr+1.
Suppose that the theorem does not hold, i.e.,χc(µ(G)) < χ(µ(G)) = r + 2. Then, by Lemma 2, there exists an(r+2)-coloring c such that Dc(µ(G)) is acyclic,
c(u) = 1, and c(x0
i) 6∈ {0, 1} for all x0i∈ V0. Note that, ifxiis a vertex ofV such that
c(xi) 6∈ {0, 1} and c(xi) 6= c(x0i), then we can replace the color of x0iwithc(xi) and
still preserveDc(µ(G)) being acyclic. Hence, we may assume that c(xi) = c(x0i) for eachxi ∈ V with c(xi) 6∈ {0, 1}.
Moreover, by Lemma 2, there exists an edgexaxb ∈ E such that {c(xa), c(xb)} =
{0, 1} and c(x0
a) = c(x0b) = t 6∈ {0, 1}. It is clear that |Va,b| ≥ d + 1, since xaxb
is an edge. Without loss of generality, we may assume thatxaxb is chosen to sat-isfy the property that|Va,b| is minimum and, under this condition, |c(Va,b)| is also minimum. Finally, we may also assume thatc(xa) = 0 and 0 = a < d ≤ b ≤ dr+12 . LetAi= {xi+dj : 0 ≤ j ≤ r} for 0 ≤ i ≤ dr. It is clear that any two vertices of
Ai, except the pair(xi, xi−1), are adjacent and, hence, have different colors. Note thatxi−1= xi+dr.
Claim 1. If xi and xj ∈ Ai \ {xi, xi−1} are vertices such that 2 ≤ |c(xi) −
c(xi−1)| ≤ r and 2 ≤ |c(xj) − c(x0j)| ≤ r, then Ai∪ {x0j} induces a directed cycle
inDc(µ(G)).
Proof of Claim 1. Sincexj ∈ Ai\ {xi, xi−1}, any two vertices of Ai ∪ {x0j}
are adjacent, except the two pairs(xi, xi−1) and (xj, x0j). Also, c(xi) 6= c(xi−1) and c(xj) 6= c(x0j) imply |c(Ai ∪ {x0j})| = r + 2. Since any two vertices of
Ai∪ {x0j} with consecutive colors are adjacent, Ai∪ {x0j} induces a directed cycle
inDc(µ(G)).
For any color k ∈ c(V ), let Vf(k),e(k) be the Vi,j of smallest size including
c−1(k) as a subset. It is clear that c(x
f(k)) = c(xe(k)) = k, but c(xf(k)−1) 6= k and
c(xe(k)+1) 6= k. Also, Vf(k),e(k)has a size at mostd, since any two vertices in it are
nonadjacent. Moreover,V = ∪k∈c(V )Vf(k),e(k)implies thatr+1 ≤ |c(V )| ≤ r+2. Claim 2. |c(V )| = r + 2.
Proof of Claim 2. Suppose to the contrary that|c(V )| = r + 1, say p 6∈ c(V )
for somep with 2 ≤ p ≤ r + 1. Let
S = {xi∈ V : 2 ≤ |c(xi) − c(xi−1)| ≤ r or 2 ≤ |c(xi) − c(xi+1)| ≤ r}.
Suppose thatp−1 6∈ c(S). Then, c(xf(p−1)) = c(xe(p−1)) = p−1 imply xf(p−1)6∈
However,c(xf(p−1)−1) 6= p − 1 and c(xe(p−1)+1) 6= p − 1 by the definition of
Vf(p−1),e(p−1). Hence,c(xf(p−1)−1) = c(xe(p−1)+1) = p−2, and so Vf(p−1),e(p−1) is a subset ofVf(p−2),e(p−2). Then,V is the union of r sets Vf(k),e(k), each of size at mostd, for k ∈ {0, 1, . . . , r + 1} \ {p − 1, p}, a contradiction to the fact that
|V | = dr + 1. This proves that p − 1 ∈ c(S). Similarly, p + 1 ∈ c(S).
We then choose a vertexxi ∈ S such that c(xi) = 1, when p = 2 and c(xi) =
p + 1 otherwise. For the case of 2 ≤ |c(xi) − c(xi−1)| ≤ r, c(Ai) = c(V ) and
{c(xi), c(xi−1)} 6= {0, 1}. Then, there exists a vertex xj ∈ Ai\{xi, xi−1} of color
0 or 1. Sincex0jis adjacent to all vertices ofAi\{xj}, the color of x0jmust bec(xj) orp. However, a vertex in V0cannot be colored by 0 or 1, hence we havec(x0j) = p. Recall that2 ≤ p ≤ r + 1 and c(xj) ∈ {0, 1}. If |c(xj) − c(x0j)| ∈ {0, 1, r + 1}, then either c(xj) = 0, p = r + 1, or c(xj) = 1, p = 2. Both cases lead to
c(xj) = c(xi), a contradiction to the fact that xi and xj are adjacent. Hence,
2 ≤ |c(xj) − c(x0j)| ≤ r. According to Claim 1, Ai∪ {x0j} induces a directed cycle
inDc(µ(G)), a contradiction. Similar arguments also lead to a contradiction for the case of2 ≤ |c(xi) − c(xi+1)| ≤ r. Therefore, |c(V )| = r + 2.
According to Claim 2,t ∈ c(V ). Since c(x00) = c(x0b) = t, we have Vf(t),e(t)⊆
V−d+1,d−1∩ Vb−d+1,b+d−1, and sod ≤ b ≤ 2d − 2 and Vf(t),e(t)⊆ Vb−d+1,d−1⊂
V0,b. Therefore,{0, 1, t} ⊆ c(V0,b).
Claim 3. For any vertexxj ∈ V0,bcolored byt, {c(xj−1), c(xj+1)} ⊆ {0, 1, t}.
Proof of Claim 3. Suppose to the contrary that there exist verticesxi, xi+1∈ V0,b
such that{c(xi), c(xi+1)} = {t, q} for some q 6∈ {0, 1, t}. Then b ≤ i+d; and both
c(x0
i−d) = ` and c(x0i+1+d) = m are not in {t, q}. If r ≥ 4, we must have ` 6= m.
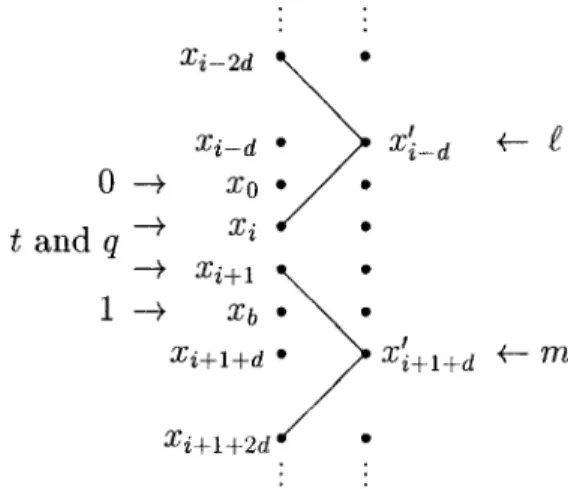
Otherwise, since every vertex of V is adjacent to at least one of x0i−d, x0i+1+d, we would have ` 6∈ c(V ), contrary to Claim 2. Hence, none of the vertices of
Vi+1+2d,i−2dcan be colored by0, 1, t, q, `, m. This implies that the dr + 1 − 4d vertices ofVi+1+2d,i−2dmust be colored by onlyr − 4 colors, a contradiction (see Fig. 1). Ifr = 3, then |Vi+1+d,i−d| = dr+1−2d = d+1 and ` = m as there are only five colors to be used. Therefore,c(xi+1+d) = 1, c(xi−d) = 0, and c(Vi+1+d,i−d) =
{0, 1, `}. It follows that xi+1+dxi−dis an edge with{c(xi+1+d), c(xi−d)} = {0, 1}
andc(x0i+1+d) = c(x0i−d), but |Vi+1+d,i−d| = d+1 ≤ |V0,b| and |c(Vi+1+d,i−d)| <
|c(V0,b)|, a contradiction to the choice of x0xb. Hence, Claim 3 holds. Claim 4. c(V0,b) = {0, 1, t}.
Proof of Claim 4. Suppose to the contrary that there exists a colorp ∈ c(V0,b) \
{0, 1, t}. Choose any xj ∈ V0,b such thatc(xj) = t. By Claim 3, c(xj−1) 6= p and
c(xj+1) 6= p. If there exists some vertex in V1,j−2 colored byp, then choose the largest integeri ≤ j − 1 such that c(xi) ∈ {0, p} and c(x0i) = p. We now consider the following three cases according to the color ofxi+1.
Case 1:. c(xi+1) = 0.
By the choice ofi, we have c(x0i+1) 6= p. Suppose that c(xi+1+d) 6= 1. Then
FIGURE 1. Vertex colors nearV0,b(for Claim 3).
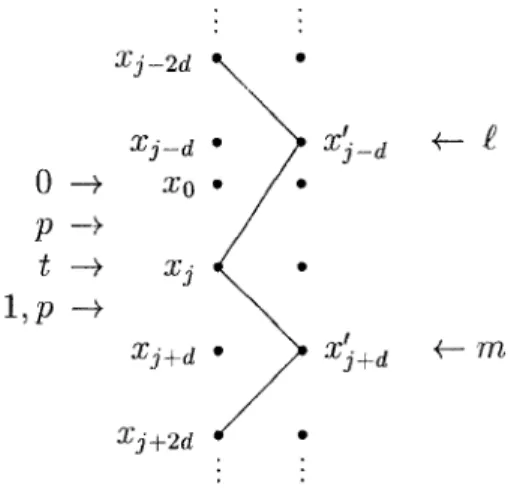
Ifr ≥ 4, then c(x0i+1+2d) = m for some m 6∈ {0, 1, p, t, q}. Hence, the dr +1−4d vertices ofVi+1+3d,i−dare colored byr − 4 colors, a contradiction (see Fig. 2). If
r = 3, then xi+1+2d = xi−d. Hence, c(xi−d) = 1 and c(x0i−d) = p. Therefore,
c(xi) = 0 and b > i + 1 + d. Since t, q 6∈ c(Vi−d,i), we have that xi−dxi is an
edge with{c(xi−d), c(xi)} = {0, 1} and c(x0i−d) = c(x0i), but |Vi−d,i| = d + 1 ≤
|V0,b| and |c(Vi−d,i)| < |c(V0,b)|, a contradiction to the choice of x0xb. Hence,
c(xi+1+d) = 1.
We now consider the set c(Vi+1,i+1+d0 ). If q ∈ c(Vi+1,i+1+d0 ) for some q 6∈
{0, 1, p, t}, then the dr + 1 − 3d vertices of Vi+1+2d,i−d are colored byr + 2 −
|{0, 1, p, t, q}| = r − 3 colors, a contradiction. Hence, c(x0
i+1) = c(x0i+1+d) = t
by Claim 2; and moreover,c(Vi+1,i+1+d) ⊆ {0, 1, t, p}.
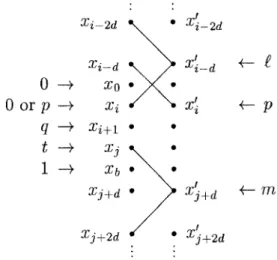
If p ∈ c(Vi+1,i+1+d), then p ∈ c(Vj+2,i+1+d), since i is maximal and since
c(xj+1) 6= p. By the assumption that p ∈ V1,j−2, we have c(x0j−d), c(x0j+d) 6∈
{0, 1, p, t}, say c(x0
j−d) = ` and c(x0j+d) = m. If r ≥ 4, then ` 6= m by Claim
2. Therefore, the dr + 1 − (4d − 1) vertices of Vj+2d,j−2d must be colored by
r − 4 colors, a contradiction (see Fig. 3). If r = 3, then ` = m by Claim 2
and|Vj+d,j−d| = (dr + 1) − (2d − 1) = d + 2. Since all vertices of Vj+d,j−d0 are colored by ` = m, we have that c(xj+d) = c(xj+d+1) = 1, c(xj−d) =
c(xj−d−1) = 0, and c(Vj+d,j−d) = {0, 1, l}. Hence, xj+dxj−d−1 is an edge with
{c(xj+d), c(xj−d−1)} = {0, 1} and c(x0j+d) = c(x0j−d−1), but |Vj+d,j−d−1| =
d + 1 ≤ |V0,b| and |c(Vj+d,j−d−1)| < |c(V0,b)|, a contradiction to the choice of
x0xb. Therefore,c(Vi+1,i+1+d) = {0, 1, t}, which also implies that xi+1xi+1+d is an edge with {c(xi+1), c(xi+1+d)} = {0, 1} and c(x0i+1) = c(x0i+1+d), but
|Vi+1,i+1+d| = d + 1 ≤ |V0,b| and |c(Vi+1,i+1+d)| < |c(V0,b)|, again a
contradic-tion to the choice ofx0xb. Case 2:. c(xi+1) = 1.
Ifc(xi) = p, then c(x0i−d) 6∈ {p, t}, say c(x0i−d) = `. Therefore, the dr + 1 − 3d vertices ofVi+1+d,i−2d are colored byr + 2 − |{0, 1, p, t, `}| = r − 3 colors, a contradiction.
Ifc(xi) = 0, then since c(x0i) = p, the dr + 1 − 2d vertices of Vi+1+d,i−d are colored byr − 2 colors, also a contradiction.
Case 3:. c(xi+1) 6∈ {0, 1, p}.
If c(xi+1) = t, then c(xi) = 0 and c(x0i) = p. Since some vertex of V1,j−2 is colored byp, we have c(x0i+1+d) 6∈ {p, t}, say c(x0i+1+d) = m. Therefore, the
dr + 1 − 3d vertices of Vi+1+2d,i−dare colored byr − 3 colors, a contradiction. If c(xi+1) = q for some q 6∈ {0, 1, p, t}, then c(x0j+d) 6∈ {0, 1, p, q, t}, say
c(x0
j+d) = m. Then we have r ≥ 4. If c(xi) = 0, then, since c(x0i) = p, the
vertices ofVj+2d,i−dare colored byr − 4 colors, a contradiction to |Vj+2d,i−d| =
dr + 1 − 3d − (j − i − 1) > dr + 1 − 4d. If c(xi) = p, then c(x0i−d) cannot be
colored by0, 1, p, q, t, say c(x0i−d) = `. Note that 0 > j − d > i − d, b < j + d, and j < d. If r ≥ 5, then |Vj+2d,i−2d| > dr + 1 − 5d and ` 6= m, i.e., at leastdr + 1 − 5d vertices of V are colored by r − 5 colors, a contradiction (see Fig. 4). Ifr = 4, then ` = m and |Vj+d,i−d| > dr + 1 − 3d = d + 1. It is clear that
c(xi−d) = 0. Since xi−2d∈ Vj+d,i−d, we have thatc(xi−2d) = 1 and c(Vj+d,i−d) =
{0, 1, `}. Therefore, xi−2dxi−dis an edge with{c(xi−2d), c(xi−d)} = {0, 1} and
c(x0
i−2d) = c(x0i−d), but |Vi−2d,i−d| = d+1 ≤ |V0,b| and |c(Vi−2d,i−d)| < |c(V0,b)|,
a contradiction to the choice ofx0xb.
By the three cases above, we conclude that no vertex ofV1,j−2 can be colored by p. A similar argument shows that no vertex of Vj+2,b−1 can be colored by p. Hence,c(V0,b) = {0, 1, t}. This completes the proof of Claim 4.
Having proved the claims, we are now ready to prove the theorem. Suppose
3 ≤ t ≤ r. Since t 6∈ c(V \V0,b), there exists an integer i such that c(xi), c(xi−1) 6∈
{0, 1, t} and 2 ≤ |c(xi) − c(xi−1)| ≤ r. Since c(Ai) = r + 1, there must be some
vertexxj ∈ Ai\ {xi, xi−1} such that c(xj) ∈ {0, 1}. Assume that c(xj) = 0 (the case ofc(xj) = 1 is similar). Since the color of x0j sayq, cannot belong to c(Ai), i.e.,q is the only color not in c(Ai) and q 6∈ {0, 1}. Hence, 1 ∈ c(Ai), some vertex
xj0 ∈ Ai\ {xi, xi−1, xj} is colored by 1, and c(x0j0) = q is clear. It follows that
either2 ≤ |c(xj) − c(x0j)| ≤ r or 2 ≤ |c(xj0) − c(x0j0)| ≤ r. By Claim 1, there is
a directed cycle inDc(µ(G)), a contradiction. Therefore, t ∈ {2, r + 1}.
Assume thatt = 2 (the case of t = r + 1 is similar). Let i be the smallest integer such thatc(xi) = 2; and let j be the largest integer such that c(xj) = 1 andi ≤ j ≤ i + d. Such a j exists. In fact, one may take j = b if there is no larger value.
For the case ofj = i + d, c(xi+d) = 1 implies c(xi−1) 6= 1. By the definition of xi, c(xi−1) 6= 2. Hence, by Claim 4, c(xi−1) = 0. Also, c(xi) = 2 implies
c(x0
i+d) 6= 2. By Claim 1, Ai∪ {x0i+d} induces a directed cycle of Dc(µ(G)), a
contradiction.
For the case ofj < i+d, c(xj+1) 6= 1 by the choice of xj; andc(xj+1) 6∈ {0, 2}, sincej + 1 > b and c(x0) = 0 and c(x00) = 2. According to 0 ≤ b − d ≤ j − d < i, we havec(xj−d) 6= 2 by the choice of xi, andc(xj−d) 6= 1 as c(xj) = 1. Hence, by Claim 4,c(xj−d) = 0. We conclude that c(x0j−d) = 2. By Claim 1, Aj+1∪ {x0j−d} induces a directed cycle ofDc(µ(G)), a contradiction.
Therefore,χc(µ(Gddr+1)) = χ(µ(Gddr+1)) = r + 2. This completes the proof of the theorem.
ACKNOWLEDGMENTS
The authors thank the referees for many constructive suggestions.
References
[1] J. A. Bondy and P. Hell, A note on the star chromatic number, J Graph Theory 14 (1990), 479–482.
[2] G. J. Chang and L. Huang, Circular chromatic numbers of distance graphs with distance sets missing multiples, Eur J Combin, to appear.
[3] G. J. Chang, L. Huang, and X. Zhu, Circular chromatic numbers and fractional chromatic numbers of distance graphs, Eur J Combin 19 (1998), 423–431. [4] G. J. Chang, L. Huang, and X. Zhu, Circular chromatic numbers of
Myciel-ski’s graphs, Discrete Math, to appear.
[5] D. C. Fisher, Fractional colorings with large denominators, J Graph Theory 20 (1995), 403–409.
[6] D. R. Guichard, Acyclic graph coloring and the complexity of the star chro-matic number, J Graph Theory 17 (1993), 129–134.
[7] L. Huang, Circular chromatic numbers of graphs, Ph.D. thesis, Dept Applied Math, Nat Chiao Tung Univ, Hsinchu, Taiwan, June, 1998.
[8] M. Larsen, J. Propp, and D. Ullman, The fractional chromatic number of Mycielski’s graphs, J Graph Theory 19 (1995), 411–416.
[9] J. Mycielski, Sur le coloriage des graphes, Colloq Math. 3 (1955), 161–162. [10] A. Vince, Star chromatic number, J Graph Theory 12 (1988), 551–559. [11] X. Zhu, Star chromatic numbers and products of graphs, J Graph Theory 16
(1992), 557–569.