Fault tolerance for Hamiltonian cycle of node
expansion on hypercube
Chun-Nan Hung Hsuan-Han Chang Guan-Yu Shi
Department of Computer Department of Computer Department of Computer
Science and Science and Science and
Information Engineering Information Engineering Information Engineering Da-Yeh University. Da-Yeh University. Da-Yeh University. spring@mail.dyu.edu.tw r9306019@mail.dyu.edu.tw r9406017@mail.dyu.edu.tw
Abstract
In this paper, we construct the variant of hypercube X(Qn, {xb, xw}) with node expansion
on one black node xband one white node xwof
hy-percube Qn = (Vb∪ Vw, E). Let F = Fb∪ Fw∪ F0
be the faulty set of X(Qn, {xb, xw}) where
Fb ⊂ Vb, Fw ⊂ Vw and F0 are disjoint sets.
We show that X(Qn, {xb, xw}) − F is
Hamil-tonian if (1).|Fb| = |Fw| = 0, |F0| ≤ n − 2,
(2).0 < |Fb| = |Fw| ≤ dn4e − 1, |F0| ≤ n − 1 − 4|Fb|,
(3).0 ≤ |Fw| 6= |Fb| ≤ dn4e−2, |F0| ≤ n−3−4fmax,
for fmax = max{|Fb|, |Fw|}. We thus derive that
X(Qn, xb, xw) is k-Hamiltonian for k = dn4e − 2.
We also investigate the fault tolerance for multi-spanning disjoint paths of complete graph Kn and
hypercube Qn.
Keywords: Hypercube; Node expansion; Fault-tolerant; k-Hamiltonian; Spanning disjoint paths.
1
Introduction
The hypercube is a popular and efficient inter-connection network. It has been widely use due to many excellent properties, such as regularity, symmetry, low diameter and degree, effective and simple routing, and so on. Component failures are unavoidable in a large parallel systems. There-fore, fault tolerance of an interconnection network is very important research issue.
The interconnection network can be expressed as a graph. The vertices on the graph repre-sent processors and edges reprerepre-sent link between processors. Let G = (V, E) be an undirected graph, where V (G) is the node set and E(G) is the edge set. The degree of a vertex v is the number of edges adjacent to v denote dG(v). A
Hamiltonian cycle(resp. Hamiltonian path) is a
cycle(resp. path) of a graph that visits every ver-tex exactly once. A graph G is a Hamiltonian
graph if there is a Hamiltonian cycle of G. A graph G = (V, E) is k-Hamiltonian if G − F is
Hamilto-nian for F ⊂ (V ∪ E) and |F | ≤ k. Some
vari-ants of hypercube are (n − 2)-Hamiltonian graphs [2, 3, 6].
A graph G = (Vb∪ Vw, E) is a bipartite graph
if each edge of E consists of one vertex from the white vertex set Vwand one vertex from the black
vertex set Vb. A bipartite graph G = (Vb∪Vw, E) is
Hamiltonian laceable if there exists a Hamiltonian
path between b, w for any b ∈ Vb, w ∈ Vw. In [7],
Tsai et al. proved that the hypercube Qn− Feis
Hamiltonian laceable for Fe⊂ E(Qn) and |Fe| ≤
n − 2.
In [5], the authors investigated the ver-tices fault-tolerance for multiple spanning disjoint paths for hypercube Qn = (Vb ∪ Vw, E). Let
Fb ⊂ Vb and Fw ⊂ Vw be two sets of faulty
vertices of Qn. Let Kb ⊂ (Vb− Fb) and Kw ⊂
(Vw− Fw) be two sets of fault-free vertices of Qn
for |Kb| + |Kw| is even. Let Kb∪ Kw= {si, ti| for
1 ≤ i ≤ |Kb|+|Kw|
2 }. The family {si, ti}
Fb,Kb
Fw,Kw is
connectable if there exist |Kb|+|Kw|
2 spanning
dis-joint paths P (si, ti), for 1 ≤ i ≤ |Kb|+|K2 w|, in
Qn− Fb− Fw. The family {si, ti}FFbw,K,Kbw is balanced
if |Kw| + 2|Fw| = |Kb| + 2|Fb|. Hung et al. proved
that every balanced family {si, ti}FFbw,K,Kbw of
hyper-cube Qnis connectable if |Fb|+|Fw|+|Kb|+|Kw| ≤
n, 4|Fb|+2|Kb| = 4|Fw|+2|Kw| ≤ n+1, for n ≥ 3.
Hung et al. presented the t-node expansion for
k-Hamiltonian graph in [4]. Let Xn be the graph
obtained by applying n-node expansion to every vertex of hypercube Qn. The authors proved that
Xn is (n − 2)-Hamiltonian in [4].
In this paper, we will prove the vertices and edges fault-tolerance for multiple spanning disjoint paths of hypercube Qn. Let Febe the set of faulty
edges of Qn. We will show that every balanced
family {si, ti}FFbw,K,Kbw of hypercube Qn− Feis
con-nectable if |Fb| + |Fw| + |Kb| + |Kw| + |Fe| ≤ n,
4|Fb| + 2|Kb| + |Fe| = 4|Fw| + 2|Kw| + |Fe| ≤ n + 1,
for n ≥ 3.
Let xb ∈ Vb and xw ∈ Vw be any two vertices
of Qn. Let X(Qn, {xb, xw}) be the graph obtained
Fb∪ Fw∪ F0 be the faulty set of X(Qn, {xb, xw})
where Fb ⊂ Vb, Fw ⊂ Vw and F0 are disjoint sets.
We will prove that X(Qn, {xb, xw}) − F is
Hamil-tonian if
1. |Fb| = |Fw| = 0, |F0| ≤ n − 2,
2. 0 < |Fb| = |Fw| ≤ dn4e−1, |F0| ≤ n−1−4|Fb|,
3. 0 ≤ |Fw| < |Fb| ≤ dn4e−2, |F0| ≤ n−3−4|Fb|.
Applying this result, we prove that
X(Qn, {xb, xw}) is k-Hamiltonian for k = dn4e − 2.
The rest of this paper is organized as follows. In section 2, we show fault tolerance for spanning disjoint paths of complete graphs. We will prove the vertices and edges fault-tolerance for multiple spanning disjoint paths of hypercube in section 3. In section 4, the fault tolerance for Hamiltonian cycle of node expansion on hypercube is proved. The conclusion is given in section 5.
2
Fault tolerance for spanning
disjoint paths of complete graph
Hung et al. proved the following lemma in [4] Lemma 1 Let Kn = (V, E) be an n-node
com-plete graph and F ⊂ (V ∪ E) be a faulty set with |F | ≤ n − 2. There exists a set V0 ⊆ V (K
n− F )
with |V0| = n − |F | such that every pair of vertices
in V0 can be joined by a Hamiltonian path.
The following theorem is the generalization of Lemma 1.
Theorem 1 Let Kn = (V, E) be an n-node
com-plete graph and F ⊂ (V ∪ E) be a faulty set with |F | ≤ n − 2. There exists a set V0 ⊆ V (K
n− F )
with |V0| = n − |F |. Such that any m pairs of
ver-tices in V0, there exist m spanning disjoint paths
of Kn− F for 1 ≤ m ≤ bn−|F |2 c.
Proof:
We prove this theorem by induction on n. Triv-ially, this theorem is true for |F | = 0, Applying Lemma 1, we can obtain that this theorem holds for m = 1. In the following, we can assume that
|F | ≥ 1 and m ≥ 2. Thus, |V0| = n − |F | ≥ 4.
Hence, we can assume n ≥ 5.
First, we consider |F ∩ V (Kn)| > 0. Let Fv
denote the set of faulty nodes. Then, the graph
Kn−F is isomorphic to Kn−|Fv|−F
0, |F0| ≤ |F |−
|Fv|. By induction hypotheses, there exists a set
V0⊆ V (K
n−|Fv|−F
0) with |V0| = n−|F
v|−|F0| ≥
n − |F |. Such that any m pairs of vertices in V0,
there exist m spanning disjoint paths of Kn− F
for 2 ≤ m ≤ bn−|Fv|−|F0|
2 c. This theorem is true
for |F ∩ V (Kn)| > 0.
Next, we consider that F ⊂ E. We only need to consider that F ⊂ E and |F | ≤ n − 4. Let H denote the subgraph of Kn given by (V, F ). Let
U = {x|x ∈ V and dH(x) > 0} and v be the
vertex in U with minimum degree. We will prove this theorem with the following three cases:
Case 1: dH(v) = 1.
In other words, there is exactly one edge of F incident to v. Thus, the graph Kn−{v}−F is
isomorphic to Kn−1− F∗with |F∗| ≤ |F | − 1.
By induction hypotheses, there exists a vertex set V0⊂ (V − {v}) with |V0| = n − 1 − |F∗|.
Such that any m pairs of vertices in V0, there
exist m spanning disjoint paths of Kn− {v} −
F∗ for 2 ≤ m ≤ bn−1−|F∗|
2 c ≤ b
n−|F |
2 c.
Since dH(v) = 1 and m ≥ 2, there exists an
edge (z1, z2) of one of these path, such that
(v, z1), (v, z2) /∈ F . Hence, we can modify
this path by replacing (z1, z2) by (z1, v) and
(v, z2), as illustrated in Figure 1. Therefore,
there exists a set V0⊆ V with |V0| = n − |F |.
Such that any m pairs of vertices in V0, there
exist m spanning disjoint paths of Kn− F for
1 ≤ m ≤ bn−|F |2 c.
Figure 1: Illustration of Case1.
Case 2: dH(v) = 2.
Since v is the vertex in U with minimum degree and dH(v) = 2, |F | ≥ 3. Thus,
n ≥ |F | + 4 ≥ 7. The graph Kn− {v} − F is
isomorphic to Kn−1− F∗with |F∗| = |F | − 2.
By induction hypotheses, there exists a ver-tex set V0⊂ (V −{v}) with |V0| = n−|F |+1.
For every m pairs of vertices in V0, there exist
m spanning disjoint paths of Kn− {v} − F∗.
Let x, y ∈ (V − {v}) and (v, x), (v, y) ∈ F . First, we consider that n = 7. Since |F | ≤
n − 4, |F | = 3. Thus, V0∩ {x, y} 6= ø.
With-out loss of generality, we can assume that
x ∈ (V0 ∩ {x, y}). We will choose two pairs
of vertices from V0. Let V∗⊂ V0 and x ∈ V∗
with |V∗| = 4. There exist two spanning
disjoint paths of Kn− {v} − F∗ between
ev-ery pair of vertices in V∗. Hence there exists
an edge (z1, z2) of these two paths such that
{z1, z2} ∩ {x, y} = ø. Thus, we can modify
the path by replacing (z1, z2) by (z1, v) and
with |V0| = n − |F |. Such that every m pairs
of vertices in V0, there exist m spanning
dis-joint paths of Kn− F for 1 ≤ m ≤ bn−|F |2 c.
This theorem is true for n = 7.
Next, we will consider that n ≥ 8. Suppose that m = 2. The number of edges of these 2 spanning disjoint paths of Kn− {v} − F∗
is at least 5. Suppose that m ≥ 3. Since
dH(v) = 2, there exists one of theses m
span-ning disjoint paths of Kn − {v} − F∗ such
that every vertex of this path is adjacent to
v. Thus, there exists an edge (z1, z2) of some
path, such that (v, z1), (v, z2) /∈ F . Hence,
we can modify this path by replacing (z1, z2)
by (z1, v) and (v, z2), as illustrated in Figure
2. Therefore, there exists a set V0 ⊆ V with
|V0| = n − |F |. Such that any m pairs of
ver-tices in V0, there exist m spanning disjoint
paths of Kn− F for 1 ≤ m ≤ bn−|F |2 c.
Figure 2: Illustration of Case2.
Case 3: dH(v) ≥ 3.
The graph Kn − {v} − F is isomorphic to
Kn−1− F∗with |F∗| = |F | − 3. By induction
hypothesis, there exists a set V0 ⊂ (V − {v})
with |V0| = n − |F | + 2. For every m pairs
of vertices of V0, there exist m spanning
dis-joint paths of Kn− {v} − F∗ for 1 ≤ m ≤
bn−|F |+22 c. Since v is the vertex of U with
minimum degree, |F | ≥ dH(v)·(dH(v)+1)
2 . The
number of edges of m spanning disjoint paths in Kn−{v}−F∗is n−m−1. Thus, n−m−1 ≥
|F | + 2m − m − 1 ≥ dH(v)·(dH(v)+1)
2 + m − 1 >
2dH(v) for dH(v) ≥ 3 and m ≥ 2. Thus, there
exists an edge (z1, z2) of one of these spanning
disjoint paths such that (v, z1), (v, z2) /∈ F .
Hence, we can modify this path by replacing (z1, z2) by (z1, v) and (v, z2), as illustrated in
Figure 3. Therefore, there exists a set V0⊆ V
with |V0| = n − |F |. Such that any m pairs of
vertices in V0, there exist m spanning disjoint
paths of Kn− F for 1 ≤ m ≤ bn−|F |2 c. 2
Figure 3: Illustration of Case3.
3
Fault tolerance for spanning
disjoint paths of hypercube
In this section, we mainly construct multiple spanning paths in hypercube with faulty vertices and edges.
An n-dimensional hypercube Qn(Vb∪ Vw, E) is
a bipartite graph whose vertices are labeled by dis-tinct n-bit binary strings. Two vertices are linked by an edge if and only if their labels differ exactly in one bit. An i-edge (x, y) is an edge that x and
y differ in the i-th bit. The hypercube Qn can be
constructed recursively as Qn = Qn−1× K2. We
can partition Qn into two subgraphs Q0n−1 and
Q1
n−1by choosing any one bit of binary string.
Let Vb be the black vertex set and Vw white
vertex set of Qn. We denote the black and white
vertex set of Qjn−1 with Vbj and Vwj, for j = 0, 1.
And let Vj = Vj
b ∪ Vwj for j = 0, 1. Thus, Vb =
V0
b ∪ Vb1, Vw= Vw0∪ Vw1, V = Vb∪ Vw= V0∪ V1.
Let Fb be the set of black faulty vertices of Qn
and Fw the set of white faulty vertices of Qn,
Fe the set of faulty edges of Qn. Similarly, we
also use Fbj and Fj
w and Fej to denote the black
and white faulty vertex set and faulty edge set of Qjn−1, respectively, for j = 0, 1. Thus, Fb =
F0
b ∪ Fb1, Fw= Fw0∪ Fw1, F0= Fb0∪ Fw0∪ Fe0, F1=
F1
b ∪ Fw1∪ Fe1, F = Fb∪ Fw∪ Fe= F0∪ F1.
In [1], Caha et al. proposed the multiple span-ning disjoint paths problem for hypercube. Let
si, ti, for 1 ≤ i ≤ k, be vertices of Qn. The
{si, ti}ki=1 is a connectable family if there exists
k spanning paths of Qn between si and ti, for
1 ≤ i ≤ k. The {si, ti}ki=1 is balanced if it has the
same number of vertices in each partite set. Caha showed that every balanced family {si, ti}ni=1 is
connectable in Q2n if the distance of every pair
si, tiis odd. Caha also showed that every balanced
family {si, ti}ni=1 is connectable in Q6n.
In [5], the authors presented the vertex fault tolerance for multiple spanning disjoint paths in hypercube. Let {si, ti}FFbw,K,Kbw be a family of G =
(Vb ∪ Vw, E) where Kb(⊂ Vb) ∪ Kw(⊂ Vw) =
{si, ti|1 ≤ i ≤ |Kb|+|K2 w|} is the set of
sets of faulty vertices. The family {si, ti}FFbw,K,Kbw
is balanced if |Kw| + 2|Fw| = |Kb| + 2|Fb|. The
family {si, ti}FFbw,K,Kbw is connectable if there
ex-ist (|Kb| + |Kw|)/2 spanning paths P (si, ti), for
1 ≤ i ≤ (|Kb| + |Kw|)/2, in G − Fb− Fw.
We also use Kbj and Kj
w to denote the set of
black and white end vertices of Qjn−1, respectively, for j = 0, 1. Let Kj = Kj b ∪ Kwj for j = 0, 1 and K = K0∪ K1. Thus, K b = Kb0∪ Kb1 and Kw = K0 w∪ Kw1. Let Kw01= {vw|vw∈ Kw0 and u ∈ K1,
for hvw, ui is a pair of K.}. Let Kb01= {vb|vb∈ Kb0
and u ∈ K1, for hv
b, ui is a pair of K.}. Let v be a
vertex of V0and U be a vertex subset of V0. We
use φ(v) to denote the neighbor of v in V1. We
further let φ(U ) = {φ(v)|v ∈ U ⊆ V0}.
The following lemma is proved in [5].
Lemma 2 Every balanced family {si, ti}FFbw,K,Kbw of
hypercube Qn is connectable if |Fb| + |Fw| + |Kb| +
|Kw| ≤ n, 4|Fb| + 2|Kb| = 4|Fw| + 2|Kw| ≤ n + 1,
for n ≥ 3.
In the following, we will investigate the vertex and edge fault tolerance for multiple spanning dis-joint paths in hypercube. We will prove the fol-lowing theorem.
Theorem 2 Every balanced family {si, ti}FFbw,K,Kbw
of Qn− Fe is connectable if |Fb| + |Fw| + |Kb| +
|Kw| + |Fe| ≤ n, 4|Fb| + 2|Kb| + |Fe| = 4|Fw| +
2|Kw| + |Fe| ≤ (n + 1), for n ≥ 3.
Proof:
When |Fe| = 0, applying Lemma 2, we can
ob-tain this theorem is hold. In the following, we will assume that |Fe| ≥ 1. We will prove this theorem
by induction on n. For n ≥ 3, we assume that every balanced family {si, ti}FFbw,K,Kbw of hypercube
Qn−1−Feis connectable where |Fb|+|Fw|+|Kb|+
|Kw| + |Fe| ≤ (n − 1), 4|Fb| + 2|Kb| + |Fe| ≤ n =
4|Fw|+2|Kw|+|Fe| ≤ n. Since Q3is 1 edge
Hamil-tonian laceable [7], this theorem is holds for n = 3. We will partition Qninto two subgraphs Q0n−1and
Q1
n−1with a bit i which some faulty edge is i-edge.
Thus, |Fj
e| ≤ |Fe| − 1 for j = 0, 1. Without loss of
generality, we can assume that |Fb| ≥ |Fw|. Thus,
|Kw| ≥ |Kb|.
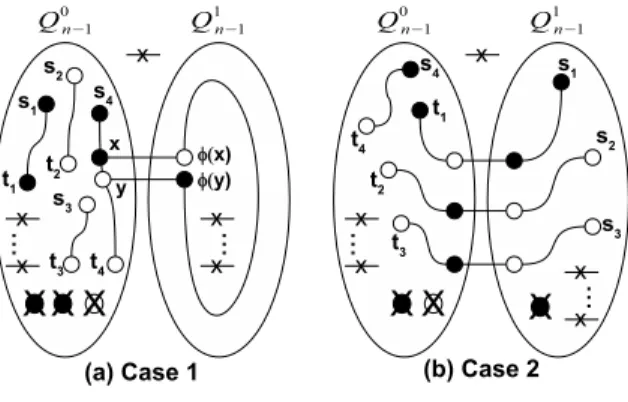
Case 1: |F0| + |K0| = 0 or |F1| + |K1| = 0
Without loss of generality, we can assume that Fb∪ Fw∪ K ∈ Q0n−1. Since |Fb0| + |Fw0| + |K0 b|+|Kw0|+|Fe|−1 ≤ (n−1), 4|Fb0|+2|Kb0|+ |Fe| − 1 ≤ n = 4|Fw0| + 2|Kw0| + |Fe| − 1 ≤ n, {si, ti}F 0 b,Kb0 F0 w,Kw0 is connectable family of Q 0 n−1− F0
e. Therefore, we can construct |K 0
b|+|Kw0| 2
spanning paths of Q0
n−1− Fe0. One of these
paths is hs1, ..., x, y, ..., t1i. There is a
Hamil-tonian path hφ(x), ..., φ(y)i of Q1
n−1 − Fe1.
Thus, we can construct |Kb|+|Kw|
2 spanning
paths of Qn−Fe, as illustrated in Figure 4.(a).
Case 2: |F0| + |K0| ≥ 1 and |F1| + |K1| ≥ 1 Let U0 b ⊂ (Vb0 − Fb0 − Kb0) with φ(Ub0) ⊂ (V1 w− Fw1− Kw1), |Ub0| = max(|Kw01|, (2|Fw0| + |K0 w|) − (2|Fb0| + |Kb0|)) and Uw0 ⊂ (Vw0 − F0 w− Kw0) with φ(Uw0) ⊂ (Vb1− Fb1 − Kb1), |U0 w| = max(|Kb01|, (2|Fb0| + |Kb0|) + |Ub0| − (2|F0 w| + |Kw0|)). Since |F0 b|+|Fw0|+|Kb0|+|Ub0|+|Kw0|+|Uw0| ≤ (n − 1), 4|F0 b| + 2(|Kb0| + |Ub0|) = 4|Fw0| + 2(|K0 w| + |Uw0|) ≤ n, {si, ti}F 0 b,K0b∪Ub0 F0 w,Kw0∪Uw0 is con-nectable family of Q0 n−1, we can construct |K0 b|+|Ub0|+|K0w|+|Uw0| 2 spanning paths of Q0n−1. Because of |F1 b| + |Fw1| + |Kb1| + |φ(Uw0)| + |K1 w| + |φ(Ub0)| ≤ (n − 1), 4|Fb1| + 2(|Kb1| + |φ(U0 w)|) = 4|Fw1| + 2(|Kw1| + |φ(Ub0)|) ≤ n, {si, ti}F 1 b,K0b∪φ(Uw0) F1
w,K0w∪φ(Ub0) is connectable family of
Q1 n−1. There exist |K1 b|+|Ub0|+|Kw1|+|Uw0| 2 span-ning paths of Q1
n−1. Therefore, we can
con-struct |Kb|+|Kw|
2 spanning paths in Qn, as
il-lustrated in Figure 4.(b). 2
Figure 4: Illustration of Theorem 2.
4
Fault Hamiltonicity for node
expansion of hypercube
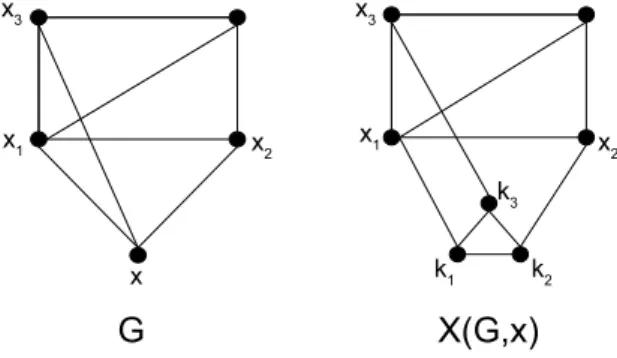
In [4], the authors defined the t-node expansion operation as follows. Let x be a vertex of graph
G = (V, E) with dG(x) = t. Let {x1, x2, · · · , xt}
be the set of neighbor of x. The t-node expan-sion X(G, x) of G on x is the graph obtained from
G by replacing x with a complete graph Kt. Let
V (Kt) = {k1, k2, · · · , kt}. That is, V (X(G, x)) =
V − {x} ∪ {k1, k2, · · · , kt} and E(X(G, x)) = E ∪
E(Kt) ∪ {(xi, ki)|1 ≤ i ≤ t} − {(x, xi)|1 ≤ i ≤ t}.
Moreover, the node expansion can be applied on a vertex subset. The node expansion of G = (V, E) on the subset U ⊆ V , denoted by X(G, U ), is the graph that is obtained from G by a sequence node expansion operations on every node u ∈ U . Let NG(x) = {(x, xi)| for all 1 ≤ i ≤ t} and
MX(G,U )(x) = V (Kt) ∪ E(Kt) ∪ {(ki, xi)| for all
1 ≤ i ≤ t} for x ∈ U . The graph G and X(G, x) are illustrated in Figure 5.
Let F be the set of faulty vertices and faulty edges of X(G, U ) and FX(x) = F ∩ MX(G,U )(x)
for x ∈ U . Let V0 ⊆ V (K
t− FX(x)) be the set
such that every m pairs of vertices in V0 there
exist m spanning disjoint paths of Kt− FX(x) for
1 ≤ m ≤ bn−|F2X(x)|c and |V0| = n − |F
X(x)|. Let
KX(G,U )−F (x) = {xi|(x, xi) ∈ E(G) and ki ∈ V0
and (xi, ki) /∈ F }. Let FXe(x) = {(xi, ki)| for ki∈/
V0 or (x
i, ki) ∈ F and 1 ≤ i ≤ t}. Let FGe(x) =
{(x, xi)| for (xi, ki) ∈ FXe(x)}. Thus |FXe(x)| =
|Fe
G(x)| = |FX(x)|.The following lemma is proved
in [4].
Figure 5: Illustration of node expansion.
Lemma 3 Given F1⊂ (V (G − x) ∪ E(G − x)). If
we delete any f edges of NG(x) from the graph G−
F1 such that the remaining graph is Hamiltonian
for f ≤ t−2, then the graph X(G, x)−(F1∪F3) is
Hamiltonian, where F3 is a subset of MX(G,x)(x)
and |F3| = f .
Let X(Qn, {xb, xw}) be the n-node expansion
of Qn = (Vb ∪ Vw, E) on {xb, xw} for xb ∈ Vb
and xw ∈ Vw. Let Knb and Knw be the complete
graphs replacing xb and xw, respectively. That is,
V (X(Qn, {xb, xw})) = Vb∪Vw∪V (Knb)∪V (Knw)−
{xb} − {xw}. Let F be the set of faulty element of
X(Qn, {xb, xw}). Let Fb = F ∩ Vb, Fw= F ∩ Vw,
F0= F −F
b−Fwand fmax= max(|Fb|, |Fw|). Let
FX(xw) = F0∩ MX(Qn,{xb,xw})(xw) and FX(xb) =
F0∩ M
X(Qn,{xb,xw})(xb). Applying the definition
of Fe
X(x), we can define that FQen(xb) = {(xb, x
i b)| for (xi b, kbi) ∈ FXe(xb)} and FQen(xw) = {(xw, x i w)| for (xi
w, kiw) ∈ FXe(xw)}. We also use FXe to denote
F0−F
X(xb)−FX(xw). We can prove the following
theorem.
Theorem 3 The graph X(Qn, {xb, xw}) − F is
Hamiltonian if 1. |Fb| = |Fw| = 0, |F0| ≤ n − 2, 2. 0 < |Fb| = |Fw| ≤ dn4e−1, |F0| ≤ n−1−4|Fb|, 3. 0 ≤ |Fw| 6= |Fb| ≤ dn4e − 2, |F0| ≤ n − 3 − 4fmax. Proof: The graph Kb
n is the complete graph replacing
xb in X(Qn, {xb, xw}). Let FKb n = F ∩ (V (K b n∪ E(Kb n)) and FKw n = F ∩ (V (K w n ∪ E(Knw)). Let Fe Qn = F e X∪ FQen(xw) ∪ F e Qn(xb). Thus |F e Qn| = |Fe X| + |FQen(xw)| + |F e Qn(xb)| = |F 0| − |F X(xb)| − |FX(xw)| + |FQen(xw)| + |F e Qn(xb)| = |F 0|. We will
prove this theorem by the following cases. Case 1: |Fb| = |Fw| = 0.
Thus |F0| ≤ n − 2. Since F = F0= F
X(xb) ∪
FX(xw) ∪ FXe, |FX(xb)| + |FX(xw)| + |FXe| ≤
n − 2. When we delete any |FX(xb)| edges
of NQn(xb) and |FX(xw)| edges of NQn(xw)
from Qn− FXe, the remaining graph is
Hamil-tonian since Qn is (n − 2)-edge
Hamilto-nian. Applying Lemma 3, X(Qn, {xb, xw}) −
Fe
X(xb) − FXe(xw) is also Hamiltonian.
Case 2: |Fb| = |Fw| > 0.
Thus |F0| ≤ n − 4|F
b|. Let FQ∗n(xb) be the
set of arbitrary |FX(xb)| edges adjacent to xb
of Qn and FQ∗n(xw) be the set of arbitrary
|FX(xw)| edges adjacent to xw of Qn. We
also denote the set F∗
Qn(xb) ∪ F ∗ Qn(xw) ∪ F e X by F∗ Qn. Since |Fb| + |Fw| + 2 + |F ∗ Qn| ≤ 2|Fb|+2+n−1−4|Fb| = n+1−2|Fb| ≤ n−1, 4|Fb| + 2 + |FQ∗n| = 4|Fw| + 2 + |F ∗ Qn| ≤ 4|Fb| + 2 + n − 1 − 4|Fb| ≤ n + 1, there exists a Hamiltonian path of Qn− Fb− Fw− FQ∗n
between every pair of vertices with odd dis-tance. Thus, Qn− Fb− Fw− FQ∗n is
Hamil-tonian laceable. This graph is also Hamilto-nian. Applying the definition of Fe
Qn, we can
know that |Fe
Qn| ≤ |F
∗
Qn|. Thus Qn− Fb−
Fw−FQenis Hamiltonian. Applying Lemma 3,
X(Qn, {xb, xw}) − Fb− Fw− F0 is also
Hamil-tonian.
Case 3: |Fb| 6= |Fw|. Thus |F0| ≤ n − 3 − 4fmax.
Without loss of generality, we can assume that |Fb| ≥ |Fw|. Thus, fmax = |Fb|. Since
FKb n⊆ FX(xb) ⊆ F 0, |F Kb n| ≤ |F 0| ≤ n − 3 −
4|Fb| ≤ n − 2. Applying Theorem 1, we can
obtain a set V0⊆ (V (Kb n) − FKb
n) with |V
0| =
n − |FKb
n|, such that any m pairs of vertices
in |V0|, there exist m spanning disjoint paths
of Kb n− FKb n for 1 ≤ m ≤ b n−|FKb n| 2 c. Since 2|Fb| + 2 − 2|Fw| ≤ 4|Fb| + 3 ≤ n − |FX(xb)|,
we will construct |Fb| + 1 − |Fw| spanning
disjoint paths P (ksi, kti) of K b n − FKb n for (ksi, xsi) /∈ FX(xb) and (kti, xti) /∈ FX(xb), 1 ≤ i ≤ |Fb| + 1 − |Fw|. Let F0 b = {xb} ∪ Fb and Kw ⊂ KX(Qn,{xb,xw})−F(xb) with |Kw| = 2(|F 0 b| − |Fw|) and Kw∩ Fw= ø. Hence |Fb0| + |Fw| + |Kw|+|FQen| = 3|Fb|+3−|Fw|+n−3−4|Fb| = n − |Fb| − |Fw| < n, 4|Fb0| + |FQen| = 4|Fw| + 2|Kw|+|FQen| = 4|Fb|+4+n−3−4|Fb| ≤ n+1.
Applying Theorem 2, we can obtain that for any |Kw| vertices there exist |K2w|
span-ning disjoint paths of Qn− Fb0 − Fw− FQen
between every pair of vertices of Kw. We
can construct |Kw|
2 spanning disjoint paths
P (xt1, xs2), P (xt2, xs3), · · · , P (xtKw |
2
Figure 6: Illustration of Theorem 3. Qn − Fb0 − Fw − FQen. Therefore, hks1 → P (ks1, kt1) → kt1, xt1 → P (xt1, xs2) → xs2, ks2 → · · · → P (xt|Kw | 2 , xs1) → xs1, ks1i forms a Hamiltonian cycle of X(Qn, xb) −
Fb − Fw− FXe − FX(xb) − FQn(xw). Thus,
X(Qn, xb)−Fb−Fw−FXe−FX(xb)−FQn(xw)
is Hamiltonian, as illustrated in Figure 6. Applying Lemma 3, we can obtain that
X(Qn, {xb, xw}) − Fb− Fw− FXe − FX(xb) −
FX(xw) = X(Qn, {xb, xw}) − F is
Hamilto-nian since |FX(xw)| = |FQn(xw)|. 2
Corollary 1 Let X(Qn, {xb, xw}) is
k-Hamiltonian where xb and xw are two vertices in
Qn with odd distance for k = dn4e − 2.
5
Conclusion
In this paper, we prove first the fault toler-ance for multi-spanning disjoint paths in complete graph Kn. When F ⊂ (V ∪ E) is a faulty set with
|F | ≤ n − 2, we show that there exist m spanning
disjoint paths in Kn− F for 1 ≤ m ≤ bn−|F |2 c.
Secondly, we discuss the fault tolerance for bal-anced and connectable property of hypercube Qn.
We show that Qn is balanced and connectable if
|Fb| + |Fw| + |Kb| + |Kw| + |Fe| ≤ n,4|Fb| + 2|Kb| +
|Fe| ≤ n+1 and 4|Fw|+2|Fb|+|Fe| ≤ n+1, for n ≥
3. Applying these results described above, we con-struct the variant of hypercube X(Qn, {xb, xw})
with node expansion on one black node xb and
one white node xw of hypercube. We prove that
X(Qn, {xb, xw}) − (Fb∪ Fw∪ F0) is Hamiltonian
if
1. |Fb| = |Fw| = 0, |F0| ≤ n − 2.
2. 0 < |Fb| = |Fw| ≤ dn4e−1, |F0| ≤ n−1−4|Fb|.
3. 0 ≤ |Fw| 6= |Fb| ≤ dn4e − 2, |F0| ≤ n − 3 −
4fmax, for fmax= max{|Fb|, |Fw|}.
Thus, we derive that X(Qn, xb, xw) is
k-Hamiltonian for k = dn
4e − 2.
Acknowledgement
The authors are grateful to the National Sci-ence Council of the Republic of China, Taiwan for
supporting this research under Contract No. NSC 95-2221-E-212-028.
References
[1] Rostislav Caha and Vclav Koubek, ”Spanning multi-paths in hypercubes,” Discrete
Mathe-matics, (2006), doi:10.1016/j.disc.2005.12.050.
[2] Wen-Tzeng Huang, Y.C. Chuang, J.M. Tan and L.H. Hsu, On the fault-tolerant Hamil-tonicity of faulty crossed cubes, IEICE
Trans-action on Fundamentals of Electronics, Com-munications and Computer Sciences Vol.
E85-A No. 6, pp.1359-1370, (2002).
[3] Wen-Tzeng Huang, J. M. Tan, C. N. Hung, and L. H. Hsu, Fault-tolerant Hamiltonic-ity of twisted cubes, Journal of Parallel and
Distributed Computing, Vol. 62, pp. 519-604,
(2002).
[4] Chun-Nan Hung, Lih-Hsing Hsu, and Ting-Yi Sung, ”On the Construction of Combined
k-Fault-Tolerant Hamiltonian Graphs,” NET-WORKS, 37(3), pp.165-170, (2001).
[5] Chun-Nan Hung and Guan-Yu Shi, ”Vertex fault tolerance for multiple spanning paths in hypercube,” Processing of the 24rd Workshop
on Combinatorial Mathematics and Computa-tional Theory, pp.241-250, (2007).
[6] J.-H. Park, H.-C. Kim, H.-S. Lim, ”Fault-hamiltonicity of hypercube-like interconnec-tion networks,” in: Proc. of IEEE
Inter-national Parallel and Distributed Processing Symposium IPDPS2005, Denver, (2005).
[7] Chang-Hsiung Tsai, Jimmy J.M. Tan, Tyne Liang, Lih-Hsing Hsu, ”Fault-tolerant hamil-tonian laceability of hypercubes,” Information