CENTERS OF CHORDAL GRAPHS

Graphs and Combinatorics 7, 305-313 (1991)

Graphs and

Combinatorics

© Springer-Verlag 1991

Centers of Chordal Graphs*

G e r a r d J. C h a n g

Department of Applied Mathematics, National Chiao Tung University, Hsinchu 30050, Taiwan, Republic of China

Abstract. In a graph G = (V, E), the eccentricity e(S) of a subset S _~ V is m a x ~ v mint ~ s d(x, y); and e(x) stands for e({x}). The diameter of G is maxx~ v e(x), the radius r(G) of G is mine v e(x) and the clique radius cr(G) is mine(K) where K runs over all cliques. The center of G is the subgraph induced by C(G), the set of all vertices x with e(x) = r(G). A clique center is a clique K with e(K) = cr(G). In this paper, we study the problem of determining the centers of chordal graphs. It is shown that the center of a connected chordal graph is distance invariant, biconnected and of diameter no more than 5. We also prove that 2cr(G)<_ d(G)< 2cr(G)+ 1 for any connected chordal graph G. This result implies a characterization of a biconnected chordal graph of diameter 2 and radius 1 to be the center of some chordal graph.

1. Introduction

I n a g r a p h G = (V, E), the distance d(x, y) from vertex x to vertex y is the m i n i m u m n u m b e r o f edges in a p a t h f r o m x to y. T h e eccentricity e(x) of a vertex x is the m a x i m u m d i s t a n c e f r o m x to a n y vertex in G. T h e diameter d(G) of G is the m a x i m u m e c c e n t r i c i t y o f a vertex in G a n d radius r(G) the m i n i m u m eccentricity. D e n o t e b y C(G) the set of all vertices whose eccentricities a r e e q u a l to r(G). T h e center of G is the s u b g r a p h ( C ( G ) ) i n d u c e d by C(G).

It was s h o w n in [7] t h a t the c e n t e r o f a g r a p h lies w i t h i n a single b l o c k ( b i c o n n e c t e d c o m p o n e n t ) , b u t need n o t be a block. As d e s c r i b e d in [ l ] , H e d e t n i e m i p r o v e d t h a t a n y g r a p h H is i s o m o r p h i c to the c e n t e r o f s o m e g r a p h G which is of d i a m e t e r 4 a n d r a d i u s 2. In fact, G can be o b t a i n e d from H b y a d d i n g four new vertices u, v, w, x such t h a t v a n d w a r e a d j a c e n t to all vertices o f H, u is a d j a c e n t o n l y to v a n d x o n l y to w. H o w e v e r , the centers o f s o m e special g r a p h s are restricted. T h e o l d e s t result is J o r d a n ' s w e l l - k n o w n t h e o r e m for trees [8]: the c e n t e r of a tree is e i t h e r K I o r K z . As a n e a s y g e n e r a l i z a t i o n we can s a y t h a t the c e n t e r of a c o n n e c t e d b l o c k g r a p h , i.e. a g r a p h w h o s e b l o c k s are c o m p l e t e g r a p h s , is e i t h e r a c u t - v e r t e x o r a block. P r o s k u r o w s k i [10] p r o v e d t h a t the c e n t e r of a m a x i m a l

* Supported by the National Science Council of the Republic of China under grant NSC77-0208-M008-05

outplanar graph is one of seven special graphs. As a generalization, in [11] he found all possible centers of 2-trees, and showed that the center of a 2-tree is biconnected.

A graph is chordal (triangulated or rigid circuit) if every cycle of length greater than three possesses a chord, i.e. an edge joining two nonconsecutive vertices of the cycle. Chordal graphs were first introduced by Hajnal and Sur~nyi [6] and then studied extensively by many people, see [5] for general results. The class of chordal graphs contains trees, block graphs, maximal outerplanar graphs and 2-trees. It was shown in [9] that the center of a chordal graph is connected. The main purpose of this paper is to study the centers of chordal graphs and to answer a part of the question given by Duchet [4]: determine the centers of chordal graphs.

Section 2 introduces the idea of clique radius cr(G) of a graph G, and proves a main theorem: 2cr(G) < d(G) < 2cr(G) + 1 for any connected chordal graph G. This result is used in Section 3 as the key for a characterization of centers of some chordal graphs.

Section 3 studies necessary and sufficient conditions for the centers of chordal graphs. In particular, we prove that the center of a chordal graph is distance invariant, biconnected and of diameter no more than 5. Finally, by using the main theorem in Section 2, we give a necessary and sufficient condition for a biconnected chordal graph of diameter 2 and radius 1 to be the center of some chordal graph.

2. Clique Centers of Chordal Graphs

A clique of a graph is a set of pairwise adjacent vertices. In a graph G = (1/, E), the distance d(x, S) from a vertex x to a set S _ F is miny~sd(x, y). The eccentricity e(S) of a set S of vertices is the maximum distance from any vertex to S. A clique center of G is a clique with minimum eccentricity which is called the clique radius of G and is denoted by cr(G). This idea is similar to bi-center which is an edge with minimum eccentricity; see Theorem 4.2 in [3].

The main result of this section is the relation between clique radius and diame- ter of a connected chordal graph. It is the keystone for determining the necessary and sufficient conditions of a chordal graph of diameter 2 and radius 1 to be the center of some chordal graph.

Theorem

2.1. 2cr(G) < d(G) <_ 2cr(G) + 1 for any connected chordal graph G =

(r,F~).

Before proving Theorem 2.1, we first list some definitions and results from [2] which are needed in this paper. Lemma 2.4 is from [9].

If d(x,y) = k is finite and 0 < m _< k, then Bet(x, m, y) denotes the set of all vertices z between x and y such that d(x, z) = m and d(z, y) = k - m. An n-sun is a chordal graph of 2n vertices with a Hamiltonian cycle (yl, zl, Y2, 2"2,..., Yn, Zn, Ya) and each Yi is of degree two. Equivalently, an n-sun is a chordal graph G = (V, E) whose vertex set V can be partitioned into Y = (Yl,-..,Y,} and Z = {z 1 .. . . . z,} such that the following three conditions hold.

(S1) Y is a stable set in G. (S2) (z 1 .. . . . z , , z l ) is a cycle in G.

Centers of Chordal Graphs 307 ($3) (Yi, zi) e E if and only if i --- j or i = j + 1 (mod n).

In the a b o v e definition, if Z is a clique, then we call the n-sun a complete n-sun. L e m m a 2.2. I f C is a cycle in a chordal graph, then for every edge (u, v) of C there is a vertex w of C which is adjacent to both u and v.

L e m m a 2.3. [2] I f G is chordal and d(x, y) = k, then Bet(x, m, y) is a clique for any O < m < _ k .

L e m m a 2.4. [9] In a chordal graph G, if K is a clique and x a vertex such that d(x, y) = k is a constant for all y e K, then Bet(z, 1, x) and B e t ( w , 1, x) are comparable for any z, w E K (i.e. one is a subset of the other); consequently, (']y~K Bet(y, 1,x) is

not empty.

Theorem 2.5. [2] 2r(G) - 2 < d(G) < 2r(G) for any connected chordal graph G.

Moreover, if 2r(G) - 2 = d(G), then G has a 3-sun as an induced subgraph. W e can also p r o v e two slightly m o r e general results as follows.

T h e o r e m 2.6. I f X and Y are two cliques in a chordal graph G such that d(x, y) = k is a constant for all x ~ X and y E Y, then Bet(X, m, Y) =- U {Bet(x, m, y): x e X and y ~ Y} is a clique for any 0 < m < k.

Proof. Consider the g r a p h G* obtained from G by adding two new vertices u and v which are adjacent to all vertices in X a n d Y respectively. T h e n G* is a chordal g r a p h a n d d(u, v) = k + 2. The t h e o r e m follows from L e m m a 2.3 and the fact that

Bet(X, m, Y) = Bet(u, m + 1, v). []

Theorem 2.7. In a chordal graph G, if K is a clique and x is a vertex such that

d(x, y) = k is a constant for all y ~ K, then Bet(z, m, x) and Bet(w, m, x) are compara- ble for any 1 ~ m <_ k and z, w ~ K; consequently, (~y~KBet(y,m,x) is not empty. Proof. The t h e o r e m is true for m = 1 by L e m m a 2.4. Suppose it is true for m - 1. Let Z = Bet(z,m - 1,x) and W = B e t ( w , m - 1,x). Z ~_ W or W _ Z by the in- duction hypothesis. T h e o r e m 2.6 implies that ZI3 W is a clique. By L e m m a 2.4, Bet(y, 1,x)'s are c o m p a r a b l e for all y ~ Z U W. Bet(z,m,x) = U r ~ z Bet(y, 1,x) and B e t ( w , m , x ) = U y ~ w B e t ( y , 1,x) then imply that Bet(z,m,x) and B e t ( w , m , x ) are

c o m p a r a b l e . [ ]

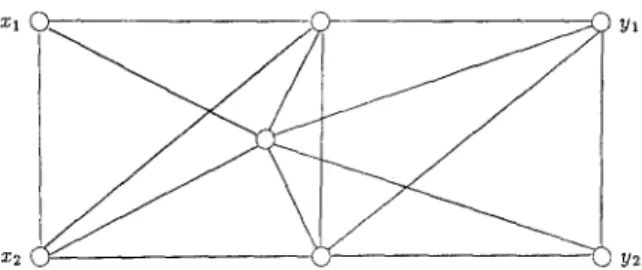
T h e g r a p h in Fig. 1 shows that Bet(x 1, 1,yl) and Bet(xz, 1,y2) are not c o m p a - rable, so we c a n n o t get a generalization of T h e o r e m 2.7 or L e m m a 2.4 by replacing vertex x by a cliue.

N o w w e are r e a d y to p r o v e the m a i n t h e o r e m of this section.

P r o o f of Theorem 2.1. C h o o s e a clique center K such that S(K) = {x e V: d(x, K) = cr(G)} has smallest n u m b e r of vertices. S u p p o s e x, y e V are such that d(x, y) = d(G). C h o o s e x*, y* e K with d(x, x*) = d(x, K) and d(y, y*) = d(y, K). Then

zl ~

Yl

x2

Y2

Fig. 1. Bet(x 1, 1, Y a) and Bet(x2, 1, Y2) are not comparable

Suppose that d(G) < 2cr(G) - 1. C h o o s e a fixed vertex w e S(K). Let K* = {w* e K: d(w,w*) = cr(G)}. Suppose K = K*, i.e. d(w,w*) = cr(G) for all w* e K. By L e m m a 2.4, there is a vertex x e (~w.~KBet(w*, 1,w). T h e n K U x is a clique center with S(K U x) c S(K) - w, a contradiction to the minimality of IS(K)L. So K* is a p r o p e r subset of K.

Next, we consider the set T = {x e V: cr(G) - 1 < d(x, K) < d(x, K*)}. If T = 2~, then K* is a clique center with S(K*) = S(K). T h e same a r g u m e n t s in the second p a r a g r a p h lead to a contradiction. So T ~ ~. F o r a n y x e T and w* e K*, choose x* ~ K - K* with d(x, x*) = d(x, K). By the definitions of K, K* a n d T, we have

cr(G) - 1 < d(x,x*) = d(x,w*) - 1 (2.1)

a n d

cr(G) = d(w, w*) = d(w, x*) - 1. (2.2)

C h o o s e shortest paths P(x,x*), P(w,w*), P(x,w) from x to x*, w to w*, and x to w respectively as in Fig. 2; where y (resp. z) is the vertex in P(x, x*)N P(x, w) (resp. P(w, w*) N P(x, w)) with largest distance f r o m x (resp. w).

X

y

2~**

Z

W

Fig. 2.

Suppose y = x*, then d(G) >_ d(x, w) = d(x,x*) + d(x*, w) >_ 2cr(G) by (2.1) a n d (2.2), a contradiction. Hence y ~ x*. Similarly, z v ~ w*. In the cycle (y . . . x*, w* . . . . ,z . . . y), by L e m m a 2.2, there is a vertex x** adjacent to b o t h x* a n d w*. N o t e that x** is n o t between y and x* (similarly, n o t between z a n d w*) otherwise d(x, w*) < d(x, x*), which contradicts (2.1). (2.1) also implies

Centers of Chordal Graphs 309 and (2.2) implies

d(w, x**) >_ d(w, x*) - 1 >_ cr(G). (2.4) (2.3) and (2.4) together with the assumption 2cr(G) - 1 >_ d(G) > d(x, w) imply that all inequalities in (2.3) and (2.4) are in fact equalities; and so x** e Bet(x*, 1, w).

N o w consider K** = K* U {x**: x e T}. It is easy to see that e(K**) <_ e(K). Since K** _~ Bet(K - K*, 1, w), by Theorem 2.6, K** is a clique. So K** is a clique center; in fact, is one with S(K**) ~ S(K) and d(w, w**) = cr(G) for all w** e K**. The same arguments as in the second p a r a g r a p h lead to a contradiction. This shows that d(G) >_ 2cr(G) and completes the proof of the theorem. [] As a consequence of Theorems 2.1 and 2.5, and the trivial inequalities cr(G) < r(G) < cr(G) + 1, for any connected chordal graph G exactly one of the follow- ing holds: 2r(G) = d(G) = 2cr(G), 2r(G) - 1 = d(G) = 2cr(G) + 1 and 2r(G) - 2 = d(G) = 2cr(G). F o r the case of block graphs, the last case is impossible since a block graph contains no 3-sun. F o r a block graph G with d(G) = 2cr(G) (resp. d(G) = 2cr(G) + 1), C(G) is a cut-vertex (resp. block); in any case C(G) is always a clique center.

3. Graphs Which Are Centers of Chordal Graphs

A chord of a path is an edge joining two nonconsecutive vertices of the path. L e m m a 3.1. In a chordal graph G, all vertices of a chordless path joining two vertices of C(G) entirely belongs to C(G).

Proof. Suppose x, y ~ C(G) and P(x, y) = (x = Vo, v l , . . . , v, = y) is a chordless x-y path. Let vi be the first vertex of P(x, y) which is not in C(G). Choose a vertex z such that d(vi, z) > r(G) and j > i as small as possible with d(vi, z) < r(G). Then d(Vk, z) > r(G) for i < k < j and d(vi_ 1, z) = d(vj, z) = r(G). Let w be the last c o m m o n vertex on shortest paths P(z, vi_l ) and P(z, vj). Then C = P(w, vi_~ ) U P(vi-~ , vj) U P(v~, w) is a cycle. By L e m m a 2.2, C has a vertex u adjacent to both vi-~ and v~. Since P(x, y) is chordless, u E P(w, vi-1) or u ~ P(vj, w). In the former case, d(z, vi) < d(z, u) + 1 = r(G) which is impossible. In the latter case, r(G) < d(z, vg) <_ d(z, u) + 1 < d(z, v~) -

1 + 1 = r(G), a contradiction. So the lemma holds. []

Theorem

3.2. The center of a connected chordal graph G is a distance invariance induced subgraph of G.

Proof. Since any shortest x-y path is chordless, the theorem follows from L e m m a

3.1. []

Theorem

3.3. The center of a connected chordal graph G is biconnected.

Proof. Suppose z is a cut vertex of the center (C(G)). Let x and y be two vertices in different components of ( C ( G ) ) - z . There are two disjoint x-y paths in G since C(G) lies in a biconnected component of G as shown in [7]. Take chords, if

there is any, to s h o r t e n these two p a t h s until two c h o r d l e s s

x-y

p a t h s are found. By L e m m a 3.1, all vertices of these two p a t h s are in

C(G).

T h e s e two p a t h s t h e n b o t h c o n t a i n the vertex z, a c o n t r a d i c t i o n . So the c e n t e r is b i c o n n e c t e d . [ ] N o t e t h a t T h e o r e m 3.3 was p r o v e d for 2-trees in [11]. By T h e o r e m 2.5, for a n y c o n n e c t e d c h o r d a l g r a p h G, there are three cases:

d(G)

= 2r(G),

d(G)

= 2r(G) - 1,

d(G)

= 2 r ( G ) - 2. W e shall d e r i v e s o m e r e s t r i c t i o n s o n d i a m e t e r s a n d r a d i i of centers of c h o r d a l g r a p h s a c c o r d i n g to these cases.

T h e o r e m 3.4.

C(G) is a clique for any connected chordal graph G with d(G)

= 2r(G).

Proof.

C h o o s e two vertices x a n d y such t h a t

d(x, y) = d(G).

F o r a n y

z ~ C(G),

we h a v e

2r(G) =

d(G) = d(x, y) < d(x, z) + d(z, y) < r(G) + r(G),

which i m p l y t h a t

d ( x , z ) = d ( z , y ) = r(G)

a n d so

z ~ Bet(x,r(G),y).

T h u s

C(G)

Bet(x, r(G), y).

T h e t h e o r e m then follows f r o m L e m m a 2.3. [ ]

I n general,

C(G)

is n o t necessarily a clique for the case of

d(G)

= 2r(G) - 1 o r 2r(G) - 2, see Fig. 3.

k

O

(a)

d(G)

= 2r(G) - 1 = 5 and

d(C(G)) = 3.

(b)

d(G)

= 2r(G) - 2 = 2 and

d(C(G)) = 2.

Fig. 3. Black vertices form

C(G)

Centers of Chordal Graphs 311

T h e o r e m 3.5.

d(C(G)) < 3 for any connected chordal 9raph G with d(G)

= 2r(G) - 1.

Proof.

C h o o s e x a n d y such t h a t

d(x, y) = d(G).

F o r a n y z ~ C(G), we h a v e

2r(G) - 1 =

d(G) = d(x, y) <_ d(x, z) + d(z, y) <

2r(G).

H e n c e

d(x, z)

a n d

d(z, y)

are e i t h e r

r(G)

- 1 o r

r(G)

b u t n o t b o t h

r(G)

- 1. W e shall p r o v e t h a t e i t h e r

z ~ Bet(x, r(G), y)

o r is a d j a c e n t to s o m e vertex in

Bet(x, r(G), y).

Since

Bet(x,r(G),y)

is a clique b y L e m m a 2.3, every two vertices o f

C(G)

are of d i s t a n c e at m o s t three in G a n d hence in

C(G).

F o r the case o f

d(x, z) = r(G)

a n d

d(z, y) = r(G) - 1, z ~ Bet(x, r(G), y).

F o r the case o l d ( x , z) =

r(G)

- 1 a n d

d(z, y) = r(G), z ~ Bet(x, r(G) - 1, y)

a n d so is a d j a c e n t to s o m e vertex in

Bet(x,

r(G), y).

S u p p o s e

d(x, z) = d(z, y) = r(G).

C h o o s e s h o r t e s t p a t h s

P(x, y), P(y, z), P(z, x)

which p a i r w i s e m e e t at x*, y*, z* as in Fig. 4. Since

r(G) > d(x,

t), r(G) >_

d(z, y)

a n d

d(x,z*) + d(z*,y) > d(x,y) >_

2r(G) - 1, we m u s t have z = z*. By L e m m a 2.2, there is a vertex w in the cycle C = ( x * , . . .

,u,z*,v ... y* ... x*)

which is a d j a c e n t to b o t h z* a n d v. If w =

u,

t h e n

d(x, u) = d(v,y)

= r(G) - 1 a n d (u, v) ~ E i m p l y

v ~ Bet(x, r(G),

y); a n d so z is a d j a c e n t to vertex v in

Bet(x, r(G), y).

If w ~ u, then w is b e t w e e n x* a n d y* as in Fig. 4. N o t e t h a t

r(G) = d(x,z*) < d(x,w)

+ 1, i.e.

d(x, w) >_ r(G)

- 1. S i m i l a r l y

d(w, y) >_ r(G)

- 1. So

d(x, w) = r(G)

o r

r(G)

- 1. In the f o r m e r case, z is a d j a c e n t to

w E Bet(x, r(G), y).

In the l a t t e r case, z is a d j a c e n t to

v ~ Bet(x, r(G), y).

This c o m p l e t e s the p r o o f o f the t h e o r e m . [ ] S i m i l a r a r g u m e n t s as in the p r o o f o f T h e o r e m 3.5 l e a d to the following result.

z, ~ ~ z

27 a ; * 'tO y * f f

Fig. 4.

T h e o r e m 3.6.

d(C(G)) < 5 for any connected chordal 9raph G with d(G)

= 2r(G) - 2. By o b s e r v i n g m a n y e x a m p l e s , we h a v e the following conjecture.

Conjecture: d(C(G))

< 2 for a n y c o n n e c t e d c h o r d a l g r a p h G with

d(G)

= 2r(G) - 2. N e x t we s t u d y sufficient c o n d i t i o n s for a b i c o n n e c t e d c h o r d a l g r a p h H to be the c e n t e r o f s o m e c h o r d a l g r a p h G. I f d ( H ) = 1 o r

d(H) = r(H)

= 2, then H is the c e n t e r o f itself. F o r the case of

d(H)

= 2 a n d

r(H)

= 1, we h a v e the f o l l o w i n g result b y using the m a i n t h e o r e m o f S e c t i o n 2.

Theorem 3.7. Suppose H = ( U , F ) is a biconnected chordal 9raph with d ( H ) = 2, r(H) = 1 and x E C(H). H is the center of some chordal 9raph G = (V, E) if and only if d ( H - x) <_ 3.

Proof. ( ~ ) S u p p o s e H is the c e n t e r of G, i.e. U = C(G). C h o o s e w e V such t h a t d(x, w) = r(G). F o r a n y z e U - x, z is a d j a c e n t to x a n d d(z, w) < r(G). H e n c e either d(z, w) -- r(G) - 1 a n d so z e Bet(x, 1, w), o r else d(z, w) = r(G). F o r the l a t t e r case, d(z, w) = d(x, w) = r(G) i m p l y , b y L e m m a 2.4, t h a t Bet(z, 1, w) N Bet(x, 1, w) ~ ;0 a n d so z is a d j a c e n t to s o m e vertex in Bet(x, 1, w). T h i s is true for all z e H. Since Bet(x, 1, w) is a cfique, d(H - x) < 3.

( ~ ) S u p p o s e d(H - x) < 3. By T h e o r e m 2.1, cr(H - x) = 1. Let K be a clique c e n t e r of H - x. T h e n every vertex in U - x is a d j a c e n t to x, a n d every vertex in U - K is a d j a c e n t to s o m e vertex in K. C o n s i d e r the g r a p h G o b t a i n e d f r o m H b y a d d i n g two new vertices u a n d v such t h a t u is a d j a c e n t to x a n d v is a d j a c e n t to all vertices of K. It is s t r a i g h t f o r w a r d to check t h a t G is a c h o r d a l g r a p h a n d H is the

c e n t e r of G. [ ]

W e close this p a p e r b y the following s u m m a r y of results: a g r a p h H is the c e n t e r of s o m e c h o r d a l g r a p h if a n d o n l y if (1) H is c h o r d a l a n d b i c o n n e c t e d a n d (2) d ( n ) = 1, o r d ( n ) = r(H) = 2, o r d(H) = 2, r(H) = 1 a n d d ( n - x) < 3 for a n y x ~ C(H), o r d(H) = 3, r(H) = 2 a n d " s o m e c o n d i t i o n s we still d o n o t k n o w " , o r d(H) = 4 o r 5 (we c o n j e c t u r e t h a t this case is impossible).

Acknowledgement, The author wishes to express his gratitude to refree for many useful suggestions about the revision of the paper.

References

1. Buckley, F., Miller, Z. and Slater, P.J.: On graphs containing a given graph as center, J. Graph Theory fi, 427-434 (1981)

2. Chang, G.J. and Nemhauser, G.L.: The k-domination and k-stability problems on graphs, SIAM J. Algebraic Discrete Meth. 5, 332-345 (1984)

3. Chang, G.J. and Nemhauser, G.L.: Covering, packing and generalized perfection, SlAM J. Algebraic Discrete Meth. 6, 109-132 (1985)

4. Duchet, P.: Discussion section for chordal graphs, Sino-Franco Conference on Combinatorics, Algorithm and Coding Theory, Taipei, November 1-6, 1987

5. Golumbic, M.C.: Algorithmic Graph Theory and Perfect Graphs, Academic Press, New York (1980)

6. Hajnal, A. and Sur~myi, J.: Ober die aufl6sung yon graphen in vollst~indige teilgraphen, Ann. Univ. Sci. Budapest g6tv6s Sect. Math. 1, 113-121 (1958)

7. Harray, F. and Norman, R.Z.: The dissimilarity characteristic of Husimi trees, Ann. Math. 58 (1), 134-141 (1985)

8. Jordan, C.: Sur les assemblages des lignes, Journal ffir die Reine and Angewandte Mathematik 70 S, 185-190 (1869)

9. Laskar, R. and Shier, D.: Construction of (r, d)-invariant chordal graphs, Congressus Numer- antium 33, 155-165 (1981)

Centers of Chordal Graphs 313

10. Proskurowski, A.: Centers of maximal outerplanar graphs, J. Graph Theory 4 (2), 75-79 (1980)

11. Proskurowski, A.: Centers of 2-trees, Annals Disc. Math. 9, 1-5 (1980)

Received: March 30, 1989 Revised: November 22, 1990