Analysis of adaptive LMS estimator with cyclic sequences in complex frequency domain

IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS-11: ANALOG AND DIGITAI

OO 5 1 0 l S 2 0 2 5 3 0 3 5 4 0

owbildhwldm(%LsB) (b) Fig. 6.

of encoding errors as a function of decimation width.

(a) Transfer function with decimation width = 40 and (b) summary

frequencies within each channel. Also, as the frequency of the folded input voltage increases, the tips of the folding waveforms tend to round-off. These effects tend to degrade the performance of any folding ADC. For example, if the rounding is such that the waveform drops below (or above) the threshold level, the circuit as described will not perform correctly. The SNS encoding however, can be directly applied to other folding techniques such as double folding

which attempt to circumvent this rounding problem. ACKNOWLEDGMENT

We would like to thank the reviewers for their very helpful comments.

REFERENCES

[l] J. Van Valburg and R. :. Van De Plassche, “An 8-b 650 MHz folding ADC,” IEEE J. Solid State Circuits, vol. 27, pp. 1662-1666, 1992. 121 P. E. Pace, P. A. Ramamoorthy, and D. Styer, “A preprocessing

architecture for resolution enhancement in high speed analog-to-digital converters,” IEEE Trans. Circuits Syst., vol. 41, pp. 373-379, June 1994. [3] J. E. Shockley, Introduction to Number Theory. New York Holt,

Rinehart and Winston, 1967.

[4] P. E. Pace and D. Styer, “High resolution encoding process for an integrated optical analog-to-digital converter,” Opt. Eng., vol. 33, pp. [5] D. Mandelbaum, “Error correction in residue arithmetic,” IEEE Trans.

2638-2645, 1994.

Comput., vol. C-21, pp. 538-545, 1972.

-

SIGNAL PROCESSING, VOL. 42, NO. 12, DECEMBER 1995 829

Analysis

of

Adaptive

LMS

Estimator with Cyclic

Sequences in Complex Frequency Domain

Ging-Shing Liu and Che-Ho Wei

Abstruct- Cyclic sequences are usually employed as the reference sequences in the adaptive filtering systems for signal or channel es-

timation. In this situation, the stability of an adaptive filter can be analyzed by an equivalent transfer function in complex frequency domain.

For several special classes of cyclic reference sequences, the stability bounds of the adaptive filter with least mean-square (LMS) algorithm and its variants, leaky-LMS (L-LMS) and minimum output variance LMS (MOV-LMS), are obtained. Effects of these algorithms on the resultant transfer functions and the stability bounds are also investigated.

I. INTRODUCTION

The least mean-square (LMS) algorithm has been well analyzed in the early works of adaplive filtering problem [l]. Most of the works consider the cases with random reference signals. However, the cyclic reference sequences with desired correlation property have been well employed in the adaptive filter for fast start-up channel estimation [2]-[6]. For an adaptive noise canceller, some cyclic sequences have also been proposed to estimate the periodic interference components corrupted on the desired signal [7]. Also, cyclic sequences are used as the reference signal in a minimum output variance mean-square estimator [8].

In [7], Glover develolped an equivalent transfer function to analyze the adaptive filter for noise cancellation. For a special class of reference inputs, the adiaptive filter can be characterized by a linear time-invariant transfer ifunction. Clarkson and White [9] generalized this approach to the adaptive LMS filter for a more general class of inputs. Although this approach can not provide high-order statistical information for the adaptive filters, it may be convenient in the stability analysis.

In this brief, we will revisit the adaptive estimator with attentions concentrated on the stability analysis. Several classes of cyclic se- quences for the adaptive LMS estimator are introduced in Section 11. Their correlation characteristics and the resulting equivalent transfer functions are derived. In Section 111, the stability issues for the adaptive filter are discussed in terms of discrete transfer function concept in complex frequency domain.

11. EQIJIVALENT TRANSFER FUNCTION FOR THE ADAPTIVE LMS ESTIMATOR A. Some Special Cyclic Sequences

To achieve fast convergence, cyclic reference sequences with flat line spectra, or equivalently impulse-like correlation functions, are more preferable. Although the use of cyclic sequences can only estimate the spectrum at equally-spaced frequency points rather than the overall frequency band, it actually conditions the estimator to reach a higher signal-to-distortion ratio such that the start-up process can be accelerated. Impulse train sequences such as {+l, 0, 0,

.

.

.

,

0} Manuscript received June 21, 1993; revised October 3, 1994 and May 13, 1995. This work was supported by the National Science Council, Republic of China, under Grant NSC-82-0404-E009-122. This paper was recommended by Associate Editor B. Kim.

The authors are wlth the Insutute of Electronlcs and Center for Telecommu- nications Research, National Chiao Tung University, Hsinchu, Taiwan, R.O.C.

Log Number 9414334.

830 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS-E ANALOG AND DIGITAL SIGNAL PROCESSING, VOL. 42, NO. 12, DECEMBER 1995

or

{+l,

-1, -1,.

. . ,

-1) [ 3 ] , 171, [8], short pseudorandom (PN) sequences 121-141, self-orthogonal sequences [5] and CORSk%lt Am- plitude and Zero Autocorrelation (CAZAC) sequences 161 are the most common candidates for the cyclic reference sequences.

Although the impulse train sequences are more straightforwad and very simple in hardware implementation, they suffer from the draw- backs of low power and large sensitivity to the noise. To overcome these problems, short PN sequences are usually considered. The use of self-orthogonal sequences for fast start-up channel estimation had been found in [5], where a large class of self-orthogonal sequences are derived from the dc-biased PN sequences. The appropriate dc bias C can be related to the sequence period N by C =

w.

In the following discussions, these cyclic sequences with the same period of

iV

= 2m - 1 will be applied to the adaptive LMS estimator.

B. Equivalent Transfer Function

In general, a mean-squared estimator implemented by adaptive filtering technique can be constructed as shown in Fig. 1. It will operate upon a reference signal to generate an estimate of the desired signal at the filter output. The tap-weight vector W k is adjusted so

that the estimation error between the desired signd d k and the output

signal Y k , e k = d k - y k = d k

-

W , ' X k , is minimized. For LMS algorithm [I], the tap-weight vector Wk is adjusted by

where p is a scalar that controls the stability and the convergence rate. For hardware implementation, the initial tap-weights are usually assumed to be zero. Accordingly, (1) becomes

i=O

Similarly, the filter output yk can be expressed by k - 1

i=O k-1

i=O

where

denotes the periodic correlation function of the cyclic sequence. Note that this correlation depends only on the relative time-difference so that the identity Y k z = yk--z holds. By using (3) and the relation

e k = d k - Y k , we obtain the following difference equation:

k - 1

ei,

+

~ L N yk-%ez = d k , k

L

1. (5)

Z=O

The summation term in the LHS of ( 5 ) implies a convolution

operation between {yk} and { e h } . By taking 2-transform upon both sides of ( 5 ) , we obtain an equivalent transfer function defined by

where

E ( z )

and D ( z ) represent the Z-tran$omzs of the error signal { e h > and the desired signal { d k } , respectively. Also, r ( z ) =

CEl

ykz is the 2-transform of the correlation function {yk) with the point at zero-lag neglected. By utilizing the periodicity in the correlation function, r ( z ) can be factored as r ( z ) = , where

f ( z )

= (y1z-l

+

y ~ z - ~

+

. . .

+

y j v - ~ a - ~ + '

+

y ~ z - ~ ) . - k ' W r e d Error Tap-Weight Control Y b Transversal Filter

I

wk

xk

Fig. 1. Adaptive LMS estimator.

Based on the relation yk = &X?-,X,, it is easy to show that the periodic correlation function { y k } can be expressed, respectively, by

k,

k = O ( m o d N )

for unipolar impulse sequence, Y k = ( 0, elsewhere.

(7a)

for bipolar impulse sequence, (7b) (7c) k = O(modN) for PN sequence, =

{

-\,

elsewhere. 1

+

&,

k = O(modN) y k = { 0, elsewhere.

for self-orthogonal sequence. (7d) By substituting (7) into ( 6 ) , the equivalent transfer function H ( z ) can

be written explicitly, respectively, by 1 - z - N 1 - (1

-

p)z-"

fir(,) =

for unipolar impulse sequence, (Sa) 1 - 2 - M

H ( 2 ) =

1

+

p ( N -

4)

'

;

:

E

z-2

+

( p N - 1)z-N

'

for bipolar impulse sequence, (8b)

for PN sequence, (8c) 1 - z-N

1

+

( p N

+

p - 1)z-"

H ( z ) =

for self-orthogonal sequence. (Sd) Since there are N zeros equally spaced on the unit-circle for H ( z )

in (8), there exists N notches in the frequency band [0,27r]. The notches indicate that the estimator can only perfectly estimate the signal or channel response at these equally-spaced frequency points rather than the overall frequency band.

m.

STABILITY BOUNDS AND OTHER CONSTRAINTS The stability of an adaptive filter is usually evaluated from the autoconelation matrix R = E { X k X T } of the reference input X k .

The algorithm is stable if the step-size p satisfies 0

<

p

<

&,

where A,,, is the largest eigenvalue of matrix R. Although the equivalent transfer function approach can not describe the behavior of the adaptive filter in all aspects, it is very convenient to determine the stability bound in terms of linear system.

It is known that the necessary condition for a digital system to be stable is that the poles of the system should be located inside the unit circle in the a-plane. The poles z, for H ( z ) in (Sa) can be easily

83 1 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS-11: ANALOG AND DIGITAL SIGNAL PROCESSING, VOL. 42, NO. 12, DECEMBER 1995

3 5 IO IS 20 S~ep-~izeNppcr-bound Sleep-sizeNppr-bound 1.5

L

e

1

t

i

_g

_0.5 U 0 2 4 6 2 8 1,s 5

3

f!

B

g

3

0,s

s

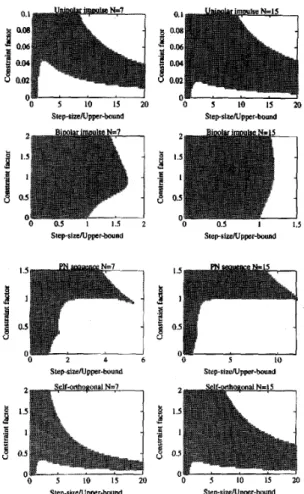
OO s IO I S 20 c Step-SizeRlpper-bund 0 0 S IO I5 20 Step-slzcNppr-bound Step-siwNppr-bund 0 5 10 IS U) Step-sizeNpper-bound

Fig. 2. Stability boundaries for the leaky-LMS estimator trained by (a) unipolar impulse (b) bipolar impulse (c) PN (d) self-orthogonal sequences with N = 7 and 15.

stable should satisfy (zpl

<

1 or, equivalently, 0

<

p

<

2 . Similarly, the stability condition for the case with self-orthogonal sequences in (8d) is given by 0

<

p

<

&.

However, it is very complicated to determine the stability bounds for H ( z ) in (8b) and (8c). In these cases, the stability bound can be found by performing Jury's test [lo], [I 11 on their characteristic equations p ( z ) . First, the characteristic equation p ( z ) for (8b) is defined from its denominator by

p ( z ) = z N

+

( p N - 4p)zN-1

+

.

.

.

+

( p N - 4 p ) 2

+

( p N

-

4 p ) z

+

( p N - 1). (9)

For the convenience in mathematical manipulation, we define A ( 0 ,N ) = 1 A ( 0 , i ) = ( p N - 4 p ) , for i = (N - I), ( N -

Z),.

. . ,2, 1. A(0,O) = ( p N - 1). (10) Also

w ,

k ) A ( j

-

1,0) A ( j - 1 , N + 1 - j - IC ) = det A ( j - 1, N

+

1

-

j) j = 1 . 2 , . . . , ( A i

-

2 ) : k = 0,1,2.

. . .

. ( N - j ) . (11) Based on (1 I), we can evaluate A(j. k ) from A ( j

-

1, k ) , recursively, for j = 1 , 2 , .

.

.

, ( N - 2).

A ( j - 1, I C )

As done in [ 111, the necessary and sufficient condition for p( z ) to

have no roots outside the unit circle can be stated by (1) P(1)

>

0

(3)

In(o,o)I <

1

(2) p(-1)

<

0 for odd N , o r y(-l)

>

0 for even N

(4) I A ( j , O ) ) > l A ( j , N - j ) l , f o r j = 1 , 2

..,..

N - 2 . (12) Since the sequence period N is assumed to be 2" - 1, the second

statement in (12) for odd N is valid. From the first three conditions, we obtain 0

<

p

<

$.

However, it is difficult to evaluate the last condition by analytic method. By computer exhaustive test as in [11], it is found that the condition is never violated. Thus, we can conclude that the first three conditions are the desired necessary and sufficient conditions. In the same manner, we can obtain the stability condition for the case with PN sequence in (8c), 0

<

p

<

$.

The stability bounds of the LMS estimator trained by these cyclic reference sequences car1 be summarized as follows:

O < p < 2 , for unipolar impulse sequence, (13a) 0

<

p

<

i\r,

2 for bipolar impulse sequence. (13b)

2

0

<

p

<

for PN sequence, ( 1 3 4

2

O < P < < , for self-orthogonal sequence. (13d) In the following, the equivalent transfer function and the stability of the adaptive filter with two variants of the LMS algorithms, leaky LMS (L-LMS) and minimum output variance LMS (MOV-LMS), will be studied. First, the leaky-LMS algorithm [ l ] controls the filter tap-weights such that the cost function J = e:

+

aWTWk(k

2

1) is minimized, where a is a constraint factor ( a

>

0). Similarly, the MOV-LMS algorithm adopts a cost function J = e;

+

a y : ( k

2

1) [8]. Differentiating J with respect to wk yields the following stochastic gradient algorithms:

wk= (1 - pcv)Wk-l

+

p e k X k , k

2

1 (L-LMS),

( 1 4 4

(14b) After some algebraic manipulations, the estimation error can be written recursively by Wk = W k - - l

+

p [ e k X k - a y k X k ] , k

2

1 (MOV-LMS). k ek = d k

-

p ek-,Xr-nXk(l

-

p ~ ) ~ - - l , n = l k

2

1 (L-LMS), (1Sa) k - 1 e k = d k

-

p

z{(l+

a ) e ,

-

a d , } X T X k , ,=O k

2

1 (MOV-LMS). (1Sb) By taking 2-transfom upon both sides of (15) and utilizing the

identity Cr=l[[m(l-ap)"-l]z-" = Al?(A) 1 - ~~-~~ ~ , we obtain the

general form of the equivalent transfer function for the two variants of the LMS algorithm as 1 H ( z ) = - (L-LMS), (16a) li-Pq&)r(*) H ( z ) =

-

-k I L a N r ( ' ) (MOV-LMS). (16b) 1 3 p ~ ( i

+

The derivation of stability bound under the tap-leakage constraint is not mathematically tractable by Jury's test method. Alternatively, it

832 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS-11: ANALOG AND DIGITAL SIGNAL PROCESSING, VOL. 42, NO. 12, DECEMBER 1995

can be evaluated from the denominator of H ( z ) in (164 by numerical manipulation. Fig. 2 shows the stability boundaries of (16a) for the cases with N = 7 and 15. The ordinate represents the constraint factor a, and the abscissa is the step-size p. To observe how the constraint factor affects the stability bounds, the step-size p is normalized to the upper-bound in the absence of constraint (CY = 0). The shaded

regions indicate the choices of ( p , CY) such that H ( z ) is stable. From

the results, it is found that the stability can be improved by using the leaky-LMS algorithm.

Second, substituting appropriate

r(z)

into (16b) and performing the Jury’s test for the MOV-LMS algorithm, the stability bounds are obtained as follows:

L

O < p < - for unipolar impulse sequence,

l + a ’

(17a) for bipolar impulse sequence, 2 O < p < - (1 +CY)” 2 O < p < - (1 +a)” O < p < (17b) for PN sequence, ( 1 7 ~ ) for self-orthogonal sequence. 2

(1

+

a)(l+ N ) ’

(17d) The upper bounds of stability in (17) decrease by a factor of (1

+

a )

from those in (13). That is, this output variance constraint reduces the upper bound of p. It is quite different from the case with tap-leakage constraint.

IV. CONCLUSION

Equivalent transfer function method is applied to the stability analysis of the adaptive LMS filter for several cyclic sequences in the signal or channel estimation. The stability bounds for the adaptive estimator with LMS algorithm and its two variants under different constraint are obtained. It is found that the leaky-LMS algorithm provides a larger stability bound compared to the LMS algorithm. In contrast, the MOV-LMS algorithm has lower stability upper-bound.

&FEFENCES

[l] S. Haykin, Adaptive Filter Theory. Englewood Cliffs, NJ: Prentice- Hall, 1991.

[2] R. W. Chang and E. Y . Ho, “On fast start-up data communication systems using pseudo-random training sequences,” Bell Syst. Tech. I.,

[3] K. H. Mueller and D. A. Spaulding, “Cyclic equalization-A new vol. 51, pp. 2013-2027, NOV. 1972.

rapidly converging equalization technique for munication,” Bell Syst. Tech. J., vol. 54, pp 36

[4] S . U. H. Quresh, “Fast start-up equalization with periodic training sequences,” IEEE Trans. Inform. Theory, vol IT-23, pp. 553-563, Sept. 1977.

[5] A. P. Clark, 2. C. Zhu, and J. K. Joshi, “Fast start-up channel estimation,” ZEE Proc. Pt. F., pp. 375-381, July 1984.

[6] A. Mewski, “Periodic sequences with optimal estimation and fast start-up equalization,” IBM

27, pp. 425-528, Sept. 1983.

171 J. R. Glover, “Adaptive noise cancelling applied ences,” IEEE Trans. Acoust., Speech, Signal P

pp. 484-4491, Dec. 1977.

[8] P. Darlington and G. Xu, “Equivalent transfer

output vanance mean-square estimators,” IEEE Trans. Signal Process.,

vol. 39, pp. 1674-1677, July 1991.

[9] P. M. Clarkson and P. R. White, “Simplified analysis of the LMS adaptation filter using a transfer function approximation,” IEEE Trans.

Acoust., Speech, Signal Process., vol. ASSP-35, pp [lo] B. C. Kuo, Digital Control Systems. Champaign, [ l 11 G. Long, F. Ling, and J. G. Proakis, “The LMS alg coefficient adaptation,” IEEE Trans. Acoust., Spe

vol. 37, pp. 1397-1405, Sept. 1989.

Correction to “Analog-Input Digital Phase-Locked Loops

for Precise Frequency and Phase Demodulation”

Ian Galton

Due to a production error in the above paper’, the manuscript received date appeared incorrectly. The correct manuscript received date should be December 13, 1993.

Manuscript received November 13, 1995.

The author is with the Department of Electrical and Computer Engineering,

EEE Log Number 9416325.

‘IEEE Trans. Czrcuits Syst. - II, vol. 42, pp. 621-630, Oct. 1995. University of California, Irvine, CA 92717 USA.