On the evaluation of attribute information for mining classification rules

On the Evaluation of Attribute Information

for

Mining

Classification Rules

Ming-Syan Chen

Electrical Engineering Department

National Taiwan University

Taipei, Taiwan,

ROC

email: mschen@cc.ee.ntu.edu.tw

Abstract

In this paper we deal with the evaluation of attribute information for mining classification rules. In a deci- sion tree, each internal node corresponds to a decision on an attribute and each outgoing branch corresponds t,o a possible value of this attribute. The ordering of attributes in the levels of a decision tree will affect the efficiency of the classification process, and should be det,ermined in accordance with the relevance of these attributes t o the target class. We consider in this pa- per two different measurements for the relevance of attributes t o the target class, i.e., znference power and znformafaon gazn. These two measurements, though

both being related t o the relevance t o the group iden- tit,y, can in fact lead to different branching decisions. It is noted that, depending on the stage of tree branch- ing, these two measurements should be judiciously em- ployed so as t o maximize the effects they are designed for. The inference power and the information gain of multiple attributes are also evaluated in this paper.

1

Introduction

Mining information and knowledge from large databases has been recognized by many researchers as a key research topic in database systems and machine learning, and by many industrial companies as an im- portant area with an opportunity of major revenues. It is noted that analysis of past transaction d a t a can provide very valuable information on customer buying behavior, and thus improve the quality of business de- cisions. It is essential to collect a sufficient amount of sales d a t a before any meaningful conclusion can be drawn therefrom. The huge amount of processed data accounts for the importance of devising efficient algo- rithms for d a t a mining.

Various d a t a mining capabilities have been ex- plored in the literature. Mining association rules has attracted a significant amount of research attention

[3, 10, 12, 16, 171. For example, given a database of sales transactions, it is desirable to discover all asso- ciations among items such that the presence of some items in a transaction will imply the presence of other items in the same transaction. Another type of d a t a mining is on ordered data, which includes searching for similar sequences [l, 181, e.g., stocks with similar movement in stock prices, and for sequential patterns

[4], e.g., grocery items bought over a set of visits in sequence. Mining on Web path traversal patterns was studied in [7]. In addition, one important application of d a t a mining is the ability t o perform classification in a huge amount of data. This is referred t o as min- ing classification rules. Mining classification rules is an approach of trying t o develop rules t o group d a t a tuples together based on certain common features. For an example of commercial applications, it is desirable for a car dealer t o know what are the common fea- tures of its most customers so that its sales persons will know whom to approach, and its catalogs of new models can be mailed directly to those customers with identified features. The business opportunity can thus be maximized.

Classification rule mining has been explored bot8h in the AI domain [13, 151 and in the context of databases

[a,

5, 8, 91. In machine learning, a decision-tree classi- fication method, developed by Quinlan [14, 151, is one of the most important results, and has been very in- fluential t o later studies. It is a supervised learning method that constructs decision trees €rom a set of examples. The quality of a tree depends on both the classification accuracy and the size of the tree. Other

approaches on data classification include statistical ap- proaches [13], rough sets approach [19], etc. In the cont,ext of dat#abases, an interval classifier has been proposed in [2] to reduce the cost of decision tree gen- eration. An at,tribute-oriented induction method has been developed for mining classification rules in rela- tional databases [9] The work in [ll] explores rule extraction in a da.ti3.base based on neural networks. A two-phase approach for classification rule mining was explored in [6], where given a large training set of data tuples, the first phase, referred t o as feature extraction phase, is applied to a subset of the train- ing database with the purpose of identifying attributes which has high relevance t o the target class. In the sec- ond phase, referred t o as feature combination phase, t,hese extracted attributes are evaluated together for a possible combined me.

In mining classification rules for a given database, one would naturally like to have a training dataset large enough so as to have a sufficient confidence on the rules derived. However, with a large train- ing set, the execution time required for rule deriva- tion could be prohibitive, in particular, when forming multi-attribute predicates is needed. When a sophis- ticated predicate is constructed from a combination of attributes, the execution time required grows expo- nentially with the size of a training database, which is highly undesirable in many applications. The fast growth in the amouat of data in those applications has furthermore made the efficient mining for classi- ficat,ion rules a very challenging issue. Consequently, in this paper we shall deal with the evaluation of at- tribute information fix mining classification rules so as t<o improve the mining efficiency.

In a decision tree, each internal node corresppnds to a decision on an attribute and each outgoing branch corresponds t o a possible value of this attribute. Each leaf node then repre,sents a target class. In order to classify a data sample with an unknown class, the clas- sifier will examine th.e attribute values of this sample along the decision tree. Clearly, the ordering of at- tributes in the levels of a decision tree will affect the efficiency of the clas:d?cation process, and should be determined in accordance with the relevance of these attributes t o the target class. The relevance of an a.t- tribute to the target class is called the inference capa-

bility of this attribute. We consider in this paper two different measurements for inference capability, i.e., in- ference power and information gain. An attribute that

is useful in inferring 1;he group identity of a data tuple

is said to have a good inference power to that group identity. On the other hand, the amount of informa- tion one can gain through branching on an attribute in a decision tree is referred t o as information gain of that attribute [15]. It is noted t8hat for an attribute, both of its inference power and its information gain are dependent upon the stage when the attribute is employed, rather than having fixed values. The use of these two measurements will be investigated in this paper. As will be shown later, these two measure- ments, though both being related to the relevance t o the group identity, can in fact lead to different branch- ing decisions. It is noted that, depending on the stage of tree branching, these two measurements should be judiciously employed so as t o maximize the effects they are designed for. In addition, in some cases the group identity is not so dependent on the value of a single attribut#e. Rather, the group identity depends on the combined values of a set of attributes. Combining sev- eral individual attributes to construct multi-attribute predicates can lead t o better inference capability. In view of this, the inference power and the information gain of multiple attributes are also evaluated in this paper.

This paper is organized as follows. A problem de- scription is given in Section 2 . Inference power and information gain of attributes are comparatively in- vestigated in Section 3. The inference capability from combined attributes is examined in Section 4. Section 5 contains the summary.

2

Problem Description

In general, the problem on mining classification rules can be stated as follows. We are given a large database W , in which each tuple consists of a set of n attributes (features), { A I , A z ,

...,

A n } . For example, attributes

could be age, salary range, gender, zip code, etc. Our purpose is to classify all data tuples in this database into different groups according to their attributes. In order to learn proper knowledge on such classification, we are given a small training database, in which each tuple consists of the same attributes as tuples in W , and additionally has a known group identity associated with it. We shall focus our discussion on the identi- fication of attributes from { A I , Aa,

...,

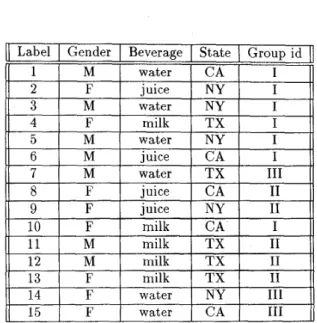
A n } that have strong relevance to the group identity.

Consider a sample profile for 15 children in Table 1 as an example. In Table 1, each tuple, correspond-

Label 1

2 3

Gender Beverage State Group id

M water CA I

F juice NY I

M water NY T

4 5

Table 1: A sample profile for classifying 15 children.

F milk T X I

M water NY I

ing to each child, contains attributes: his/her gender, beverage preferred and state lived, and additionally his/her group identity (i.e., class). (For ease of expo- sition, each tuple is given a label in its first column, which is, however, not part of the attributes.) We now would like t o analyze the relevance between the attributes (i.e., gender, beverage and state in this c u e ) and the group identity. As stated before, an attribute

that is useful in inferring the group identity of a data tuple is said t o have a good inference power to that group identity. Also, the amount of information one can gain through branching on an attribute in a de- cision tree is referred to as information gain of that attribute. A p r e d i c a t e in this study means a classifica- tion rule used t,o classify data tuples in the database

w.

12 13

14 15

As described earlier, in a decision tree, each inter-

nal node corresponds t o a decision on an attribute and each outgoing branch corresponds t o a possible value of this attribute. Each leaf node then represents a tar- get class. In order t o classify a data sample with an unknown class, the classifier will examine the attribute values of this sample along the decision tree. Specifi- cally, we shall focus on evaluating the inference capa- bility, i.e., inference power and information gain, of in- dividual attributes for the target class in an attribute- oriented induction procedure.

M milk T X I1

F milk T X I1

F water NY I11

F water CA I11

3

Comparing Inference Power

with Information Gain

We shall compare, for given attributes, their inference powers with their information gains. The procedure to determine the inference powers of attributes is pre- sented in Section 3.1, and that t o obtain the informa- tion gains of attributes is presented in Section 3.2.

3.1

Identifying Attributes with Good

Inference Power

Suppose A is an attribute and { a l , a 2 , ..., a,} are m

possible values of attribute A. Also, the domain of the group identity g is represented by domain(g)= { w l ,

212, ..., ~~~,,~,,(~)l}. The p r z m a r y group for a value a,

of attribute A , denoted by

was,

is the group that has the most tuples with their attribute A= a,. Explicitly,

use T L A ( U % , wk) to denote the number of tuples which are in group v k and have a value of a, in their attribute A. Then, we have

The primary group for each value of attribute

A can hence be obtained. For the example pro- file in Table 1, if A is “gender,” then domain(A)=

{Male

,

Female}

,

and n~ (Male ,I) =4, n~ (Male ,II) = 2

,

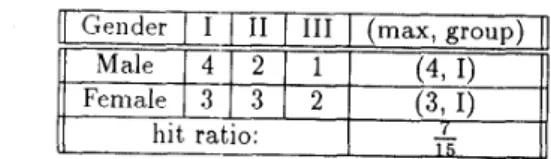
and nA(Male,III)=l. Group I is therefore the primary group for the value “Male” of the attribute “gender”. The hit ratio of attribute A, denoted by h ( A ) , is

defined as the percentage of tuples which, according to their corresponding attribute values, fall into their primary groups. Let N denote the total number of tuples. Then,

It can be seen that the stronger the relationship be- ’tween an attribute and the group identity, the larger the hit ratio of this attribute will be. A hit ratio of an attribute would become one if that attribute could uniquely determine the group identity. The hit ratio is a quantitative measurement for the inference power of an attribute. According t o the primary groups of various values of an attribute, the hit ratio of that at- tribute can be determined. The most distinguishing attribute refers to the attribute with the highest hit ratio.

I Ih U

Table 2: Distribution when the profile is classified by ge t i d cr

Table 4: Distribution when the profile is classified by

beverage.

s Table t,a t e. 3: Dist,ribut8ioii when the profile is classified by

,,,,//I\.\~.,

\\\\

-,,\~

Slntc

For illu~trat~ive purposes, consider the example pro- / /” \

(.‘A

[’)

(

1

NY

i‘)

.I‘X file i n Table 1. First, we classify this profile according

t,o gender, and obtain the results in Table 2. As ex- value “Male” of attribute “gender”. Also, it can be seen t,ha.t, Groups I and I1 are tied for the number of tuples which have “1;lemale” as the value of their at- t,ribut,e “gender”. In t,his case, either Group I or Group I1 can be t,he primar:! group for the value “Female” of att,rihut,e “gender”. t i s a result, there are 7 tuples, out, of 15 t~uples, falling into their primary groups. The hit ratio of a.tt,ribute gender is thus

A.

pla.ined earlier, Group I is the primary group for the

/

”[

.)\

/

1

.;\,

/

.I

+yc,.;,gc

/

Figure 1: Part of the decision tree with state as the first level branching attribut.e.

Next,, we classify this profile according to state, and obtain t.he primary group for each value of attribute st.a.t.e. T h e result,s in ‘Table 3 follow. Consequently, the

hit &io for att,ribute statme is

6.

Following the same procedure, we cia.ssify t,he profile in Table 1 according t.o beverage, and oht,zin the results in Table 4. It can he verified by Table 4 that the hit ratio of beverage is

A .

Fiimlly, having t,he largest hit ratio among the t,hree at,tributes, stat,e is t,he most distinguishing at- tribute in this example. Part of the decision tree with state as t,he first level branching attribute is given in Figure 1. The data sets when the values of state are

C A and NY are given in Tables 5 and 6, respectively.

3.2

Identifying Attributes with High

Information Gain

As a typical decision tree procedure, ID-3 employs

a top-down irrevocable strategy that searches only part of the search space [llj] Being an information- theoretic approach with the purpose of minimizing the

1

Label

1

Gender

1

Beverage

I

Group id

[J

water

juice juice

10 F milk

15 F water

Table 5 : The data set when state = CA.

1

Label

I

Gender

I

Beverage

I

Group id

1

1

2

1

F l juice

I

I

n

water water

14 F water I11

traveling time in the decision tree, ID-3 branches on the at,t,ribute with t8he highest information gain so that the further information required for classifying data samples with unknown classes is minimized.

Consider a d a t a set P of p d a t a samples. Suppose the classifying attribute has m distinct classes Pi,

15

i

5

m, and there are pi d a t a samples for each class Pi.

Then, the information needed t o classify a given d a t a sample is:

m

An attribute A with values a l , a,, ..., a k can be used

to partition

P

into C1,

Cz,

..., C k , where Cj contains

those d a t a samples in P that have value a j of A . Let

Cj have p i j d a t a samples of class Pi. The expected

information based on the partitioning by A is given by:

It can be seen that I ( p l j , ..., p,j) is the information required t o classify d a t a samples in C j . The informa-

t8ion gain by branching on attribute A is thus gain(A)=

I ( P 1 , P a , . . . I P m ) - E ( A ) .

Consider the example in Table 1. We now exam- ine the information gain by branching on different at- tributes. Before the first branching, the information required is

7 7 5 5 3 3

15 15 15 15 15 15

1 ( 7 , 5 , 3 ) = -(-lo~~-+-log:,-+-lOg~-) = 1.506. Using attribute state in the first level:

Using state as the branching attribute, we have

{ a ~ , u ~ , u ~ } ={CA, NY, TX}, and C1 consists tuples with label I , 6, 8, 10 and 15, as shown in Table 5, where the numbers of tuples following into Groups I, I1 and I11 are 3 , 1, and 1, respectively. C2 and 6‘2

can be obtained similarly. For notational simplicity, we use I S t n t e = C A to represent I s t a t e = c ~ ( 3 , 1 , l ) . We then have,

3 3 1 1 1 1

5 5 5 5 5 5

I S t a t e = N y = -(-log,-

+

-log,-

+

-log,-) = 1.371

The value of gain(state) is then

1(7,5,3)-E(state)=0.135.

Using attribute beverage in the first level: Following the same procedure, we have,

E ( B e v e r a 9 e ) = & I b e v e r a g e = j u i e e

+

& I b e v e r a g e = w a t e r + & I b e v e r a g e = m i l k = 0.99.

The value of gain(beverage) is

then 1(7,5,3)-E(beverage)=0.516. Similarly, we can obtain the information gain for attribute gender and learn that beverage is the attribute with the highest information gain. It is worth mentioning that though state, as determined in Section 3.1, is the attribute with the largest hit ratio, beverage is the attribute with the highest information gain.

Note that though both being related t o the rele- vance to the group identity, inference power and infor- mation gain are in fact designed t o achieve different effects. The inference power of an attribute mainly means “For an arbitrary tuple, what is the probability that we can guess correctly the group identity of this tuple based on the value of that attribute?” In con- trast, the information gain of an attribute is a mea- surement that takes into account the complexity of classifying !tuples even after having branched on this attribute. In other words, the inference power is in essence a one-step measurement

,

whereas the infor- mation gain does consider the execution effort for the

later process. It should be noted, however, the pro- cess of using information gain to build a decision tree is also greedy in nature. How to select a proper mea- surement is indeed a system-dependent issue. In some database applications, instead of using all attributes of data samples, we may only want t o employ a subset of attributes for classification, as a trade-off between the completeness of classification and the execution effi- ciency. In that case, one may want t o have a combined

.I 11 3 5 7 14 15

M

1: FA I: M

F

hl NY I

iv

NY I

M

T X I11 17 NY I11 17 CA I11 L Li Figure 2 : Part. of t,he decision t,ree with beverage as t,h e fi rs t, 1 eve1 branching at, tr i b u t,e .

[ m i ~ e n d e r

I

State

1

Group id

1

CA

F NY

Table 7: The da1,a set when beverage = juice.

use of inforniat~ion gain and inference power for the branching of a decision tree. On possible scenario is to ident,ifji the first few attributes by information gain and t,o use inference power as a measurement for those internal nodes not. to be further partitioned. Clearly,

ot,her scenarios for t,he combined use of these two mea- surement,s are conceivable, depending upon the syst,ein environ,nient, and t,he corresponding objectives.

Part. of t.he decision t.ree with beverage as the first level lira.nching at,trikute is given in Figure 2. The data set,s when the values of beverage are juice and water are given in Tables 7 and 8, respectively.

-;ider

I

State

I

Group id

U

II

1

I

i\4

I

CA

I

I

n

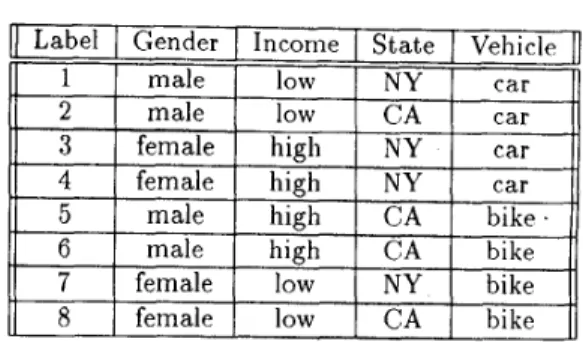
Table 9: A sample profile for preferred vehicles.

4

Combined Attribute

Informa-

tion

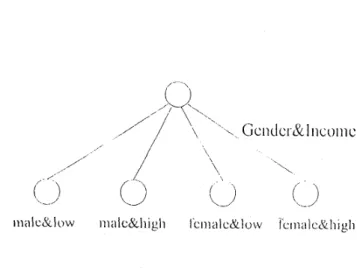
As mentioned earlier, in some cases the group ident,ity is not so dependent on the value of a single att,ribute, but instead, depends upon the combined values of a set. of attributes. This is particularly true in t,he presence of those athibutes tha.t have strong relevance among themselves. Consider the profile in Table 9 as a.n ex- ample. In Table 9 , it is found that a male with low income and a female with high income usually drive cars, whereas a male with high income and a female with low income ride bikes. In this c a e , exploring t2he relationship between “vehicle” (corresponding to the group id in Table 1) and “either gender or income at- tribute” will lead to little results, since neither gender nor income has a good inference capability to the ve- hicle. However, a combination of gender and income (e.g., a male and low income) indeed has a good infer- ence capability, in t8erms of botjh inference power and information gain, t80 t,he vehicle.

Consider the profile in Table I for example. As stated in Properties €I and G below, the resulting in- ference capability of a 2-attribute predicat<e will always be greater than or equal to that of each participat,ing attribute. It can be obtained from Table 10 that for the attribute pair (gender,state), the hit ratio is

A.

Similarly, it can be obtained that the hit ratio of (gen- der,beverage) is

E.

It is interestring to see that at.- tribut,e pair (gender,beverage), though not containing the most distinguishing attribute state, actually has a better inference power than (gender,state).

By generalizing the procedure in Section 3.2, we can

determine the information gain of multiple at.t,ributes.

It can be verified that (gender,beverage) is in fact the 2-at.tribute pair that ha.s the highest information gain among all 2-attribute pairs. It is noted that to identify

. -

Gender and State male & CA m a l e & N Y

I I1 I11 (max, group)

2 0 0 ( 2 , 1) 2 0 0 ( 2 , 1) female & CA female & NY (1, I’, Y -

Table 10: Combining genders and states to classify the profile in Table 1.

such a 2-attribute pair with the highest information gain, one has to consider the information gain of ev- ery 2-attribute pair. An example for this phenomenon can be found in Table 9, where state is the attribute with the highest, information gain when individual at- tributes are considered. T h e attribute pair (gender, in- come), which does not contain state, is the 2-attribute pair with the highest information gain, whose branch- ing is shown in Figure 3 . Note that such a branching will not, be employed if one uses state for the first level branching.

Property H: Let a and j3be two disjoint sets of at- tributes, with hit ratios h ( a ) and h(,B), respectively. Also, use h ( a

Up)

to denote the hit ratio of the at- tribute set Then, the value of h(aUP) is bounded

by:

1nax{h(a),h(P))

I

h ( a U P )

5

1, in which both the upper and lower bounds are tight bounds.

It. can be seen that the right inequality follows from the definition of a hit ratio. We now consider the left inequality. Without loss of generality, assume that

h ( a ) 2 h ( P ) . Let ai be one set of values for attributes in a , and i j j be one set of values for attributes in

p.

cy(

+

/?j represents one set of values for attributes in

cy UP. naup(cyi

+

Pj

,

v k ) denotes the number of tuples which are in group V k and have a value of ai

+

pj in

their at,tribute set, a U ,B. u U t + P ~ represents the pri- mary group of t h e set of values ai

+

pj in attribute

set a U /3.

maXvkEdomain(g) n,ua(ai

+

Pj ,

uuk), which implies

C p j E d o r r a a i n ( / 3 ) n a u o ( @ i + h ’ v c u i + P ~ )

2

n,(ayi, U,). We

Then, we have naup(a;

+

p j , ~ ” . + ~ j

I=

in turn obtain h ( a U P ) = C c r , E d o m a i n ( , ) C p J E d o n a i n ( P ) n,up(..; f P j , V , ’ + P J )

2

Cw,Edonain(a)

n,(a;,

= h ( a ) , leading to the left inequality. It can be ver- ified that the tightness of the right inequalities can be achieved.

Figure 3: Part of the decision tree when the first level attribute combines gender and income.

Similarly, by omitt,ing its straightforward proof, we have the following property for the information gain from combined attributes.

Property G : Let cy and /3 be two disjoint sets of at,-

tributes, with information gain I ( @ ) and 1(/3), respec- tively. Also, use I ( a U

p)

to denote the information gain of the attribute set CY U

p.

Then, the value of

I ( a U

p)

is bounded by:

m a x M f f ) ,

I ( P H

I

I ( f f U P ) .

5

Conclusion

In this paper we have dealt with the evaluation of at- tribute information for mining classification rules. It is noted that the ordering of attributes in the levels of

a decision tree will affect the efficiency of the classifi- cation process, and need be determined in accordance with the relevance of these attributes to the target class. We evaluated in this paper two different mea- surements for the relevance of attributes to the target class, i.e., inference power and information gain. It is shown that these two measurements, though both be- ing related to the relevance to the group identity, can in fact lead to different branching decisions. It is not,ed t h a t , depending on the stage of tree branching, these two measurements should be judiciously employed so as to maximize the effects they are designed for. Also,

a combined use of these two measurements can be em- ployed to improve the overall efficiency of the decision tree process. In addition, the inference power and the information gain of multiple attributes have been ex- amined in this paper.

Acknow1edge:ment s

M.-S. Chen is in part supported by National Science Council, Project No. NSC 88-2213-E-002-041 and Project No. 88-2219-13-002-003, Taiwan, ROC.

Databases. IEEE Transactions on Knowledge and Data Engzneerzng, pages 29-40, February 1993.

[lo] J . Han and Y. Fu. Discovery of Multiple-Level Association Rules from Large Databases. Pro- ceedings of the 21th Internatzonal Conference on Very Large Data Bases, pages 420-431, Septem-

ber 1995.

References

R. Agrawal, C. Faloutsos, and A. Swami. Efficient Similarity Search in Sequence Databases. Proceed- ings of th.e 4th Intl. conf. on Foundations of Data Organization and Algorithms, October, 1993.

R. Agrawal, S. Ghosh, T. Imielinski, B. Iyer, and A. Swami. An [nterval Classifier for Database Mining Applications. Proceedings of the 18th International Conference on Very Large Data Bases, pages 560--573, August 1992.

R. Agrawal and R. Srikant. Fast Algorithms for Mining Association Rules in Large Databases.

Proceedings of ihe 20th International Confer- ence on Very Large Data Bases, pages 478-499,

September 1994.

R. Agrawal and R. Srikant. Mining Seqiien- tial Patterns. Proceedings of the 11th Interna- tional Conference on Data Engineering, pages 3-

14, March 1995.

T.M. Anwar, H.W. Beck, and S.B. Navathe. Knowledge Mining by Imprecise Querying: A Classification-Based Approach. Proceedings of the 8th International Conference on Data Engineer- ing, pages 622-630, February 1992.

M.-S. Chen. Using Multi-Attribute Predicates for Mining Classification Rules. Proceedings of 22nd Annual Intern'l Computer Software and Applica- tion Conference, August 19-21 1998.

M.-S. Chen, J.-S. Park, and P. S. Yu. Efficient Data Mining for Path Traversal Patterns. IEEE Transactions on Knowledge and Data Engineer- ing, 10(2):209-221, April 1998.

J . Han, Y. Cai,

,

and N . Cercone. Knowledge

Discovery in Dat.abases: An Attribute-Oriented Approach. Proceedings of the 18th International Conference on Very Large Data Bases, pages 547- 559, August 1992.

J . Han, Y. Cai, and N. Cercone. Data Driven Discovery of Quantitative Rules in Relational

[11] H. Lu, R. Setiono, and H. Liu. NeuroRule: A Connectionist Approach to Data Mining. Pro- ceedzngs of the 21th Internatzonal Conference on Very Large Data Bases, pages 478-489, Septem-

ber 1995.

[12] J -S. Park, M.-S. Chen, and P. S. Yu. Using a

Hash-Based Method with Transaction Trimming for Mining Association Rules. IEEE Transactaons on Knowledge and Data Engzneerzng, 9(5):813-

825, October 1997.

[13] G. Piatetsky-Shapiro. Discovery, Analysis and Presentation of Strong Rules. Knowledge Dascov- ery zn Databases, pages 229-238, 1991.

[14] J. R Quinlan. C4.5: Programs for Machzne Learnzng. Morgan Kaufmann, 1993

[15] J.R. Quinlan. Induction of Decision Trees. Ma- chzne Learnzng, 1:81-106, 1986.

[la] A. Savasere, E. Omiecinski, and S. Navathe. An Efficient Algorithm for Mining Association Rules in Large Databases. Proceedzngs of the 21th Inter- nataonal Conference on Very Large Data Bases,

pages 432-444, September 1995.

[17] R. Srikant and R. Agrawal. Mining Generalized Association Rules. Proceedzngs of the 21th Inter- natzonal Conference on Very Large Data Bases,

pages 407-419, September 1995.

[18] J . T.-L. Wang, G.-W. Chirn, T.G. Marr, B. Shapiro, D. Shasha, and K. Zhang. Com- binatorial Pattern Discovery for Scientific Data: Some Preliminary Results. Proceedangs of A CM SIGMOD, Manneapolzs, M N , pages 115-125, May, 1994.

[19] W. Ziarko. The discovery, analysis, and repre- sentation of d a t a dependancies in databases. In G . Piatetsky-Shapiro and W. J. Frawley, editors,

Knowledge Dascovery an Databases, pages 195- 209. AAAI/MIT Press, 1991.