A NEURAL FUZZY SYSTEM WITH LINGUISTIC TEACHING SIGNALS

IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3, NO. 2, MAY 1995 ₁₆₉

A Neural Fuzzy System with

Linguistic Teaching Signals

Chin-Teng Lin, Member, ZEEE,

and

Ya-Ching Lu

Abstract-A neural fuzzy system learning with linguistic teach- ing signals is proposed in this paper. This system is able to process and learn numerical information as well as linguistic information. It can be used either as an adaptive fuzzy expert system or

as an adaptive fuzzy controller. At first, we propose a five- layered neural network for the connectionist realization of a fuzzy inference system. The connectionist structure can house fuzzy logic rules and membership functions for fuzzy inference. We use a-level sets of fuzzy numbers to represent linguistic information. The inputs, outputs, and weights of the proposed network can be

fuzzy numbers of any shape. Furthermore, they can be hybrid of fuzzy numbers and numerical numbers through the use of fuzzy singletons. Based on interval arithmetics, two kinds of learning schemes are developed for the proposed system: fuzzy supervised learning and fuzzy reinforcement learning. They extend the normal supervised and reinforcement learning techniques to the learning problems where only linguistic teaching signals are available. The fuzzy supervised learning scheme can train the proposed system with desired fuzzy input-output pairs which are fuzzy numbers instead of the normal numerical values. With fuzzy supervised learning, the proposed system can be used for rule base concentration to reduce the number of rules in a fuzzy rule base. In the fuzzy reinforcement learning problem that we consider, the reinforcement signal from the environment is linguistic information (fuzzy critic signal) such as “good,” “very good,” or “bad,” instead of the normal numerical critic values such as “0” (success) or “-1” (failure). With the fuzzy critic signal from the environment, the proposed system can learn proper fuzzy control rules and membership functions. We discuss two kinds of fuzzy reinforcement learning problems: single- step prediction problems and multistep prediction problems. Simulation results are presented to illustrate the performance and applicability of the proposed system.

I. INTRODUCTION

OME observations obtained from a system are precise,

S

while some cannot be measured at all. Namely, two kinds of information are available. One is numerical information from measuring instruments and the other is linguistic informa- tion from human experts. Some data obtained in this manner are hybrid; that is, their components are not homogeneous but a blend of precise and fuzzy information.

Neural networks adopt numerical computations with fault- tolerance, massively parallel computing, and trainable prop- erties; however, numerical quantities evidently suffer from a

lack of representation power. Therefore, it is useful for neural networks to be capable of symbolic processing. Most learning Manuscript received July 8, 1994; revised December 9, 1994. This work was supported by the National Science Council, Republic of China, Contract The authors are with the Department of Control Engineering, National IEEE Log Number 9410129.

NSC 82-0408-E-009-429.

Chiao-Tung University, Hsinchu, Taiwan, Republic of China.

methods in neural networks are designed for real vectors. There are many applications that the information cannot be represented meaningfully or measured directly as real vectors. That is, we have to deal with fuzzy information in the learning process of neural networks. Fuzzy set is a good representation form for linguistic data. Therefore, combining neural networks with fuzzy set could combine the advantages of symbolic and numerical processing. In this paper, we propose a new model of neural fuzzy system that can process the hybrid of numerical and fuzzy information.

In general, the learning methods can be distinguished into three classes: supervised learning, reinforcement learning, and unsupervised learning. In supervised learning, a teacher pro- vides the desired objective at each time step to the learning system. In reinforcement learning, the teacher’s response is not as direct, immediate, and informative as that in supervised learning and serves more to evaluate the state of system. The presence of a teacher or a supervisor to provide the correct response is not assumed in unsupervised learning, which is called “learning by observation.” Unsupervised learning does not require any feedback, but the disadvantage is that the learner cannot receive any external guidance and thus is inefficient, especially for the applications in control and decisionmaking. Hence, in this paper we are interested in the supervised and reinforcement learning capabilities of the neural fuzzy system.

Most of the supervised and reinforcement learning meth- ods of neural networks, for exaxnple the perception [l], the

BP (backpropagation) algorithm [2] and [3], and the A R - p

algorithm [4], process only numerical data. For supervised learning problems, some approaches have been proposed to process linguistic information with fuzzy inputs, fuzzy outputs, or fuzzy weights. Ishibuchi and his colleagues have proposed a series of approaches and applications with the capacity of processing linguistic input or/and linguistic output [5]-[7]. In their methods, the weights, inputs, and outputs of the neural network are fuzzified using fuzzy numbers represented by a-level sets. They derived learning algorithms from a cost function defined by the a-level sets of actual fuzzy outputs and target fuzzy outputs. Hayashi et al. [8] presented a similar method with fuzzy signals and fuzzy weights by using triangular fuzzy numbers. A learning algorithm was derived from a nonfuzzy cost function. Hayashi et al. [9] also proposed a similar architecture of neural network with fuzzy weights and fuzzy signals, but the learning algorithm was complete different from the proposed methods of Ishibuchi. In their method, the BP learning algorithm is directly fuzzified based

I70 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3, NO. 2, MAY 1995

on a fuzzy-valued cost function; i.e., the rule for changing fuzzy weights is defined by fuzzy numbers.

The common points of the above approaches are summa- rized as follows: 1) The a-level sets of fuzzy numbers are used to represent linguistic inputs, linguistic outputs, fuzzy weights, or fuzzy biases. 2) The operations in neural networks are per- formed by using interval arithmetic operations for a-level sets.

3) Fuzzy numbers are propagated through neural networks.

4) Fuzzy weights are usually triangular or trapezoidal fuzzy numbers. Because the real number arithmetic operations in the traditional neural networks are extended to interval arithmetic operations for a-level sets in the above fuzzified networks, the computations become complex (e.g., multiplication of interval) and time-consuming. Moreover, since fuzzy numbers are propagated through the whole neural network, the time of computations and the required memory capacities are 2h times of those in the traditional neural networks, where h represents the number of quantized membership grade. In this paper, we attack this problem by allowing numerical signals to flow in the proposed network internally and reach the same purpose of processing fuzzy numbers.

For reinforcement learning problems, almost all existing learning methods of neural networks focus their attention on numerical evaluative information [4], [ 101-[22]. Inspired by Klopf s [22] work and earlier simulation results [19], Barto and his colleagues used neuron-like adaptive elements to solve difficult learning control problems with only scalar reinforce- ment signal feedback [14]. They also proposed the associative reward-penalty ( A R - P ) algorithm for adaptive elements called AR-P elements [12]. Several generalizations of A R - P al- gorithm have been proposed [20]. Williams formulated the reinforcement learning problem as a gradient-following pro- cedure [18], and he identified a class of algorithms, called REINFORCE algorithms, that possess the gradient ascent property; however, these algorithms still do not include the full A R - P algorithms. Recently, Berenji and Khedkar [15] proposed a fuzzy logic controller and its associated learning algorithm. Their architecture extends Anderson’s method [ 161 by including a priori control knowledge of expert operators in terms of fuzzy control rules. Lin and Lee [lo] also proposed a connectionist architecture, called R”-FLCS, for solving vari- ous reinforcement learning problems. The R”-FLCS can find proper network structure and parameters simultaneously and dynamically. All the above reinforcement learning schemes assume scalar critic feedback (scalar reinforcement signal) from the environment. In this paper, we shall attack the fuzzy reinforcement learning problem where only fuzzy critic signal (e.g., “good,” “very good,” “bad.”) is available. This problem is much closer to the expert-instructing learning system in real world than the original one with scalar critic signal.

The objective of this paper is to explore the approaches to supervised learning and reinforcement learning of neural fuzzy systems which receive only linguistic teaching signals. At first, we propose a five-layered feedforward network for the network realization of a fuzzy inference system. This connectionist structure can house fuzzy logic rules and mem- bership functions, and perform fuzzy inference. We use a-level sets of fuzzy numbers to represent linguistic information. The

inputs, outputs, and weights of the proposed network can be fuzzy numbers of any shape. Since numerical values can be represented by fuzzy singletons, the proposed system can in fact process and learn hybrid of fuzzy numbers and numerical numbers. Based on interval arithmetics, two kinds of learning schemes are developed for the proposed system. They are fuzzy supervised learning and fuzzy reinforcement learning. They generalize the normal supervised and reinforcement learning techniques to the learning problems where only linguistic teaching signals are available. The fuzzy super- vised learning scheme can train the proposed network with desired fuzzy input-output pairs (or, equivalently, desired fuzzy IF-THEN rules) represented by fuzzy numbers instead of numerical values. With supervised learning, the proposed system can be used for rule base concentration to reduce the number of rules in a fuzzy rule base.

In the fuzzy reinforcement learning problem that we con- sider, the reinforcement signal from the environment is lin- guistic information (a fuzzy critic signal) such as “good,” “very good,” or “bad,” instead of the normal numerical critic values such as “0’ (success) or “-1” (failure). There are two major problems embedded in the reinforcement learning problems [lo]: 1) there is no instructive feedback from the environment to tell the network how to adapt itself, and 2) (fuzzy) reinforcement signal may only be available at a time long after a sequence of actions has occurred (the credit assignment problem). To solve reinforcement learning problems in neural fuzzy systems, we integrate two of the proposed five-layered networks into a function unit. One net- work (action network) acts as a fuzzy controller that performs fuzzy stochastic exploration to find out its output errors. The other network (evaluation network) acts as a fuzzy predictor that uses the fuzzy temporal difference technique to predict the output errors for either single or multistep prediction. It also provides a more informative and in-time internal fuzzy reinforcement signal to the action network for its learning. After finding the output errors, the developed supervised learning scheme can be applied directly to train both the action and evaluation networks. Hence, with fuzzy critic signal from the environment, the proposed fuzzy reinforcement learning system can learn proper fuzzy control rules and membership functions.

This paper is organized as follows: Section I1 describes the fundamental properties and operations of fuzzy numbers and their a-level sets. These operations and properties will be used in later derivation. In Section 111, the structure of our neural fuzzy system is proposed. A fuzzy supervised learning algorithm for the proposed system is presented in Section IV. The learning algorithm contains structure and parameter learning phases. In Section V, a fuzzy reinforcement learning scheme is developed. We consider the learning methods in two situations: single-step prediction problems and multistep pre- diction problems. In Section VI, two applications are simulated to illustrate the practical effect of the proposed neural fuzzy system. One is rule base concentration for knowledge-based evaluator (KBE) with fuzzy supervised learning. The other is the cart-pole balancing problem with fuzzy reinforcement learning. Finally, conclusions are summarized in Section VII.

LIN AND LU: A NEURAL FUZZY SYSTEM WITH LINGUISTIC TEACHING SIGNALS

membership grade 4

X d x‘i

(a) (b)

Fig. 1. Representations of fuzzy number. (a) d e v e l sets of fuzzy number. (b) discretized (pointwise) membership function.

n.

REPRESENTATION OF LINGUISTIC INFORMATION When constructing information processing systems such as classifiers and controllers, two kinds of information are available. One is numerical information from measuring in- struments and the other is linguistic information from human experts. We can naturally indicate the numerical information using real numbers. But, how to represent the linguistic data? It has been popular for using fuzzy sets defined by discretized (pointwise) membership functions to represent linguistic infor- mation (see Fig. l(b)). Fuzzy sets, however, can be defined by the families of their a-level sets according to the resolution identity theorem (see Fig. l(a)). In this paper, we use a- level sets of fuzzy numbers to represent linguistic information because of their advantages in both theoretical and practical considerations [23]-[25]. From theoretical point of view, they effectively study the effects of the fuzziness and the position of a fuzzy number in a universe of discourse. From practical point of view, they provide fast inference computations by using hardware construction in parallel and require less memory capacity for fuzzy numbers defined in universes of discourse with a large number of elements; they easily interface with two-valued logic; and they allow good matching with systems that include fuzzy number operations based on the extension principle.

Let us first review some notations and basic definitions of fuzzy sets. We use the uppercase letter to represent a fuzzy set and the lowercase letter to represent a real number. Let x be an element in a universe of discourse X. A fuzzy set, P, is defined by a membership function, p p ( z ) , as p p : X -+ [0, 11. When X is continuum rather than a countable or finite set, the fuzzy set

P

is represented as P =

sx

p p ( z ) / z , where x E X.

When X is a countable or finite set, P = Z ; p p ( x ; ) / z ; ,

where z; E X . We call the latter form as a discretized or pointwise membership function. A fuzzy set, P, is normal when its membership function, p p ( z ) , satisfies the condition

max,: p p ( x ) = 1. A fuzzy set P is convex if and only 0

5

X

5

1,z1 E X , x 2 E X . The a-level set of a fuzzy set P, P,, is defined by

if IlP(XZ1

+

(1

-

X ) Q )

2

m i n [ P P ( x l ) , P P ( Q ) ] , where

= { 4 P P ( Z )

2

a> (1) where 0

4

a

5

l , x E

X.

A fuzzy set P is convex if and only if every P, is convex; that is, P, is a closed interval of

R. It can be represented by

P, = [ P p , P ‘ p ] (2)

where a E [ 0 , 1 ] . A convex and normalized fuzzy set whose

~

171

membership function is piecewise continuous is called a fuzzy number. Thus, a fuzzy number can be considered as containing the real numbers within some interval to varying degrees. Namely, a fuzzy number

P

may be decomposed into its a- level set, Pa, according to the resolution identity theorem [26] as follows

P = U a P , , = u a [ p j “ ) , p p ) ]

01 (2

=

s,

S t P aPPa

(%I/..

(3)

We shall next introduce some basic operations of a-level sets of fuzzy numbers. These operations will be used in the derivation of our model in the following sections. More detailed operations of fuzzy numbers can be found in [27].

Addition: Let A and B be two fuzzy numbers

and A, and B, their a-level sets,

A

= U,aA, =

U,a[up),up)],B = U,aB, = U,a[bj”),bp)]. Then we

can write

A,(+)B, = [ u p ’ , u p ’ ] ( + ) [ b p ) , b p ) ]

= [U?)

+

b p , u p )

+

b p ] . (4) Subtraction: The definition of addition can be extended to the definition of subtraction as follows.

A,(-)B, = [ u ~ ’ , u ~ ) ] ( - ) [ b ~ ) , b ~ ) ]

= ( a ) - b p , $1 - bl“)]. (5) Multiplication by an Ordinary Number: Let A be a

fuzzy number in R and k an ordinary number k E R. We have

Multiplication: Here we consider multiplication of fuzzy numbers in

Rf

, Consider two fuzzy numbers A and B in

R+

.

For the level a, we have

The reader is referred to [27] for the general case that A and

B are fuzzy numbers in

R.

Difference: We can compute the difference between fuzzy numbers A and B by

diff(A, B ) =

~ [ ( U Y ’

- bp))’

+

( u p ) - b p ) ) ’ ] . (8) Defuuijication: In many practical applications such as control and classification, numerical (crisp) data are required. That is, it is essential to transform a fuzzy number to a numerical value. The process of mapping a fuzzy number into a nonfuzzy number is called “defuzzification.” Various defuzzification strategies have been suggested in [28], [29]. In this section, we describe two methods (MOM, COA) that transform a fuzzy number in the form of a-level sets into a crisp value.

0

Mean of Maximum Method (MOM)

The mean of maximum method (MOM) generates a crisp value by averaging the support values whose

172 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3, NO. 2, MAY 1995

membership values reach the maximum. For a discrete universe of discourse, this is calculated based on the membership function by

2

where 1 is the number of quantized z values which reach their maximum membership value.

For a fuzzy number 2 in the form of a-level sets, the defuzzification method can be expressed according to (9) as

where defuzzifier represents a defuzzification operation. Center of Area Method (COA)

Assuming that a fuzzy number with a pointwise mem- bership function p z has been produced, the center of area method calculates the center of gravity of the distribution for the nonfuzzy value. Assuming a discrete universe of discourse, we have

j = 1

For a fuzzy number 2 in the form of a-level sets, it can be expressed according to (1 1) as

defuzzifier(2) = zo = ’ (12)

a l a _&

cy

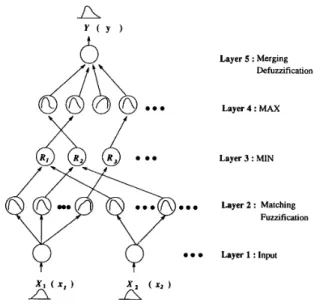
111. BASIC STRUCTURE OF THE NEURAL FUZZY SYSTEM In this section, we construct an architecture of neural fuzzy system that can process fuzzy and crisp information. Fig. 2 shows the proposed network structure which has a total of five layers. This five-layered connectionist structure performs fuzzy inference effectively. Similar architectures have been proposed in [lo], [30], and [31]. Nodes at layer one are input nodes whose imports are fuzzy numbers or crisp numbers. Each input node corresponds to one input linguistic variable. Layer five consists of output nodes whose export are also fuzzy numbers or crisp numbers. Each output node corresponds to one output linguistic variable. Nodes at layers two and four are term nodes which define membership functions representing the fuzzy terms of the respective linguistic variable. Only the nodes at layer two and four have fuzzy weights. Each node in layer two executes a “match” action to find the match degree between the input fuzzy number and the fuzzy weight if the input is linguistic information. If the input is a crisp number, they execute a “fuzzification” operation to map the input value from an observed input space to the fuzzy weights in nodes at layer two. Each node at layer three is a rule node which

Layer 5 : Merging Defuzzification

Layer 4 : MAX

h

h

*.. Layer 3 : MIN

om. Layer 2 : Matching

Fuzzification

0 0 0 Layer 1 : Input

Fig. 2. The five-layered architecture of the proposed neural fuzzy system.

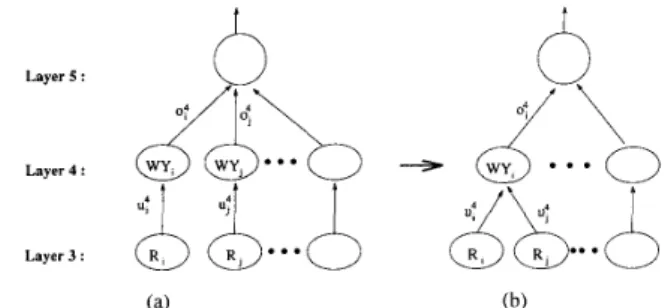
represents one fuzzy rule. Hence, all the layer-3 nodes form a fuzzy rule base. Links from layers two to three define the preconditions of the fuzzy rules, and links from layer three to four define the consequents of the fuzzy rules. Therefore, for each rule node, there is at most one link (maybe none) from or to some term node of a linguistic node. This is true both for precondition links and consequent links. The links at layers two and five are fully connected between linguistic nodes and their corresponding term nodes. If linguistic outputs are expected, each node in layer five “merges” all fuzzy weights connected to it, scaled by the output values of layer four, to produce a new fuzzy number. If numerical output values are required, each layer-5 node executes a “defuzzification” operation to obtain a crisp decision.

We shall next describe the signal propagation in the pro- posed network layer by layer following the arrow directions shown in Fig. 2. This is done by defining the transfer function of a node in each layer, Signal may flow in the reserve direction in the learning process as we shall discuss in the following sections. In the following description, we shall consider the case of single output node for clarity. It can be easily extended to the case of multiple output nodes. A typical neural network consists of nodes, each of which has some finite fan-in of connections represented by weight values from other nodes and fan-out of connections to other nodes (see Fig. 3). The notations U and U represent the input crisp and

fuzzy numbers of a node, respectively. The notations o and 0 represent, respectively, the output crisp and fuzzy numbers of a node. The superscript in the following formulas indicates the layer number.

Layer 1 (Input): If the input is a fuzzy number, each node in this layer only transmits input fuzzy number X; to the next layer directly. No computation is done in this layer. That is

0: =

U

a [ ~ : , ( ~ ) , o:icy)] =

X;

=

U

cx[xL:), x!;’]. (13)

LIN AND L U A NEURAL FUZZY SYSTEM WITH LINGUISTIC TEACHING SIGNALS

-

173

Fig. 3. Basic structure of a node in the proposed neural fuzzy system.

If the input is a crisp number xi, it can be viewed as a fuzzy singleton, i.e.,

a a

Note that there is no weight to be adjusted in this layer. Layer 2 (Matching): Each node in this layer has exactly

one input from some input linguistic node, and feeds its output to rule node(s). For each layer-2 node, the input is a fuzzy number and the output is a numerical number. The weight in this layer is a fuzzy number W X i j . The index i, j means the j t h term of the ith input linguistic variable

Xi.

The transfer function of each layer-2 node is,

a

+

( W s g - ? p ) 2 ] , (15)

02. 2.7 a ( f ? , ) 2 3 = e - ( f , 2 , ) 2 / 2 g 2 (16) where o is the variance of the activation function a(.). It is a constant given in advance. The activation function U ( . ) is a nonnegative, monotonically decreasing function of f$ E [0, CO], and a(0) is equal to 1. For example, a ( . ) can also be given alternatively as

02, 23 a(f?.) 23 =

rf."J

(17)

where O < r < l , or

where X is a nonnegative constant. The output of a layer-2 node indicates the matching degree of input and fuzzy weight. It is noted that the matching process in this layer is different from that in the conventional fuzzy control systems [29]. In the conventional fuzzy control systems, we usually consider numerical input data, and thus the matching process is simply the calculation of a membership function value. If we view a numerical value as a fuzzy singleton, then our formula in the above will achieve the same result as the conventional approach dose.

Layer 3 (MZN): The input and output of a node in this layer are both numerical. The links in this layer perform pre- condition matching of fuzzy logic rules. Hence, the rule nodes should perform fuzzy AND operation. The most commonly used fuzzy AND operations are intersection and algebraic product [29]. If intersection is used, we have

(19)

03

= min(u;, U ; , . .

.

,

U",.

On the other hand, if algebraic product is used, we have

0; = U:.;.

.

.U;. (20)

Similar to layer one, there is no weight to be adjusted in this layer.

Layer 4 (MAX): The nodes in this layer should perform fuzzy OR operation to integrate the fired rules which have the same consequent. The most commonly used fuzzy OR operations are union and bounded sum 129). If the union operation is used, we have

of = max(u;,ui,...,u:)

.

(21) If the bounded sum is used, we have

04

= min(1, ut

+

U ;

+

. . .

+

U",. (22) The input and output of each layer-4 node are both numerical values.

Layer 5 (MergingDefuuiJcation): In this layer, each node has a fuzzy weight WU,. There are two kinds of operations in this layer. When we need a fuzzy output Y , the following formula is executed to perform a "merging" action xu:.

wu,

0 5 =

U'a[O:(a),O;(a)~

y =

.

(23) a i Namely

Y =

U

'a[yp), yp'], WU; =

U

'~[wY,!;', wy,!;)] (24)

a a

where

a

a

If the output of the neural fuzzy system is required to be a numerical value, the output node executes the defuzzification action. The following formulas simulate the Tsulcumoto' s defuzzification method 1321 fi =defuzzifier(WY,) = a 1 (27) 2 T ' a L a x u : ui

f

i 2 where

174 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3. NO. 2, MAY 1995

In the rest of this paper, we call the above proposed five-layered neural network with fuzzy output as “Fuzzy Connectionist Architecture with Linguistic Output” (FCLO), and that with numerical output as “Fuzzy Connectionist

Ar-

chitecture with Numerical Output” (FCNO). From the above description we observe that only layer-1 inputs and layer-5 outputs of the FCLO and FCNO are possibly fuzzy numbers (in the form of a-level sets). Real numbers are propagated internally from layer two to layer four in the FCLO and FCNO. This makes the operations in our proposed network less time-consuming as compared to the neural networks that can also process fuzzy input/output data but require fuzzy signals flowing in them.

IV. SUPERVISED LEARNING ALGORITHM In this section, we shall derive supervised learning al- gorithms for the proposed neural fuzzy system (FCLO and FCNO). These algorithms are applicable to the situations that pairs of input-output training data are available. We allow the training data (either input or output) to be numerical values (vectors), fuzzy numbers, or mixture of them. When the system is trained to be a fuzzy controller or fuzzy classifier, the input and desired output are usually numerical values. On the other hand, when the system is trained to be a fuzzy expert system, the input and desired output are usually fuzzy numbers (linguistic information). In this case, the fuzzy input- output training pairs can be regarded as fuzzy if-then rules and the trained neural fuzzy system is like a (condensed) fuzzy knowledge base. Consider for example the following two training fuzzy if-then rules

R I : IF z1is small and 2 2 is large, THEN y is good,

R2: IF 2 1 is large and z2 is small, THEN y is bad. Then the corresponding two input-output training pairs are “(small, large; good)” and “(large, small; bad),” where the fuzzy terms are defined by given fuzzy numbers in the form of a-level sets. In general, the fuzzy rules for training are

Rp: IF z1 is X,, and

. . .

and 2 , is

X,,,,

THEN y is Yp

where p = 1 , 2 ,

.

.

. ,

m , and m is the total number of train- ing rules. These fuzzy if-then rules can be viewed as the fuzzy input-output pairs, (X,I

,

X,,,

. . .

,

X,,,;

Y,), where p = 1 , 2 , .

. .

,

m. If the input or output are crisp data, the corre- sponding fuzzy elements in the training pairs become numer- ical elements.

With the supervised learning algorithm that we shall de- velop, the proposed system can learn fuzzy if-then rules from numerical data. Moreover, it can learn fuzzy if-then rules from experts’ linguistic knowledge represented by fuzzy if- then rules. This means that it can learn to represent a set of training fuzzy if-then rules using another smaller set of fuzzy if-then rules. This is a novel and efficient approach to rule combination. The proposed neural fuzzy system can thus be used for rule base concentration to reduce the number of rules. This provides a useful tool for designing a fuzzy knowledge base. A knowledge base is usually contributed by several domain experts, so duplication of if-then rules is inevitable.

We thus usually need to compress the rule base by combining similar rules into representative rules.

Before the learning of the neural fuzzy system, an initial network structure is first constructed. Then during the learning process, some nodes and links in the initial network are deleted or combined to form the final structure of the network. At first, the number of input (output) nodes is set equal to the number of input (output) linguistic variables. The number of nodes in the second layer is decided by the number of fuzzy partitions of each input linguistic variable z;, IT(zz)I, which must be assigned by the user. The fuzzy weights W X ; j in layer two are initialized randomly as fuzzy numbers. One better way is to distribute the initial fuzzy weights evenly on the interested domain of the corresponding input linguistic variable. As for layer three of the initial network, there are

II;lT(x;)l

rule nodes with the inputs of each rule node coming from one possible combination of the terms of input linguistic variables under the constraint that only one term in a term set can be a rule node’s input. This gives the preconditions of initial fuzzy rules. Finally, let us consider the structure of layer four in the initial network. This is equivalent to determining the consequents of initial fuzzy rules. Let the number of nodes in layer four be the same as the number of rule nodes in layer three. Also, the fuzzy weights in layer four are assigned randomly. The connections from layer-3 nodes to layer-4 nodes is one-to-one initially. That is, each layer-3 node is connected to its respective layer-4 node. Some of layer-4 links and nodes will be eliminated properly in the structure learning process which will be described in Subsections IV-B. With the above initialization process, the network is ready for learning. We shall next propose a two-phase supervised learning algorithm for our five-layered neural fuzzy system. In phase one, a parameter learning scheme is used to adjust the fuzzy weights. In phase two, a structure learning scheme is used to delete or combine some nodes and links in the neural fuzzy system.

A. Parameter Learning Phase

A gradient-descent-based backpropagation algorithm pre- sented in [33] and [34], is employed to adjust fuzzy weights in layer two and layer four of the proposed network. If the FCLO is used, the error function to be minimized is

where Y = U , a [ y p ) , y p ) ] is the current fuzzy output and

D = U , a [ d p ) , d p ) ] is the desired fuzzy output. If the FCNO

is used, the error function to be minimized is

e = i ( d - y), (31)

where y is the current output and d is the desired output. We

assume that W = U , a [ w ~ ) , w ~ ) ] is the adjustable fuzzy parameter in layer two and layer four. Then to update fuzzy weights means to update the parameters tup) and tup). we shall next derive the update rules for these parameters layer

I75

LIN AND L U A NEURAL FUZZY SYSTEM WITH LINGUISTIC TEACHING SIGNALS by layer based on the general learning rule

(32)

w(t

+

1) = w(t)

+

77

where w represents w p ) or w g ) , and Q is the learning rate. Layer 5: If an FCLO is used and the desired output is fuzzy number Y, the update rules of wy,!;' and wyj;) are derived from (25) and (26) as follows

The error signal to be propagated to the preceding layer is de

(43) Layer 4: In this layer, there is no weights to be adjusted. Only the error signals need to be computed and propagated. If an FCLO is used, the error signal

:

6

is derived form (21)

b5 = - = (y - d ) . de d e ay?) U: dY

-

(yl")

-

d?)) -

--

'

(33) x u : (a)

-

7

-

-

dwyil ay, a w y p Up

.

(34) as follows -- - ( & Y ) - @ ) ) 2

aC(ep)

+

e?)) d w y p dyd") dwyj;)

6

:

= - de - i de de

The error signals to be propagated to the preceding layer are ₌

C(6y

₊

_{6 p )}

₍₄₄₎

do! -

where

(37) (38)

If an FCNO is used and the desired output is numerical value y, the update rules of the parameters are derived form

(27) and (28) as follows = 1 ( 0 ) 2(YI - d1"')2,

ep)

= 1. (a) JY2 - dd"')2. where and where (45) (46)

If FCNO is used, the error signal

6

:

is derived from (21) as follows

Layer 3: As in layer four, only the error signals need to be computed. According to (19), this error signal

6

:

can be derived as

de de do4

63 =- - -2

dog - do4 do?

(48)

S,",

if

04

= max(u;1,.

. .

,

U",,,

176 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3, NO. 2, MAY 1995

where

and

When fuzzy weights are adjusted by (33)-(53), two unde- sirable situations may happen. That is, the lower limits of the a-level sets of fuzzy weights may exceed the upper limits, and the updated fuzzy weighted may become nonconvex. To cope with these undesirable situations, we perform necessary modifications on the updated fuzzy weights to make sure that they are legal fuzzy numbers after updating. This process is described as follows.

Procedure: F u u y Number Restoration:

Inputs: Fuzzy weights W = U , a [ w p ) , w P ) ] adjusted

Outputs: The modified fuzzy weights W =

by (33)-(53).

U c u a [ 6 p ) ,

wp)]

which are legal fuzzy numbers.

Step 1. k = 1,

if wrk)

>

wp), then wik) - - w2

(‘I

and

wp)

= (kc) _w1

7

1 w1 w2

.

else ,&(‘I = ( k ) and

wp)

= (‘1 Step 2. For IC = h - 1 downto 0, do

if w ( k / h )

>

,,jjy+l/h) then ,&iklh) = A ( k + l / h )

,

w1 >

else w(”W = ( k / h )

w1

,

(a)

Fig. 4. Illustration of consequent combination.

A. Term-node combination scheme: Term-node combina- tion is to combine similar fuzzy terms in the term sets of input and output linguistic variables. We shall present this technique on the term set of output linguistic variables. It is applied to the term set of input linguistic variables in exactly the same way. The whole learning procedure is described as follows:

Step 1. Perform parameter learning until the output error is smaller than a given value; i.e., e

5

errordimit, where error-limit is a small positive constant.

Step 2. If diff(WY,,WY,)

5

similar-limit and

similar-limit is a given positive constant, remove term node j with fuzzy weight WU, and its fan-out links, and

connect rule node j in layer 3 to term node i in layer four

(see Fig. 4).

Step 3: Perform the parameter learning again to optimally

adjust the network weights.

The term-set combination scheme in Step 2 can automati- cally find the number of fuzzy partitions of output linguistic variables.

The operations in Step 2 can be equally applied to the term set of input linguistic variables.

B. Rule combination scheme: After the fuzzy parameters and the consequents of the rule nodes are determined, the rule combination scheme is performed to reduce the number of rules. The idea of rule combination is easily understood through the following example. Consider a system contains the following fuzzy if-then rules

RI : IF 21 is small and 22 is small, THEN y is good,

R2: IF 21 is medium and 22 is small, THEN y is good,

RJ: IF 21 is large and 5 2 is small, THEN y is good and

if w p l h )

<

cp+l/h),

then &?Ih) = w2

else @ / h ) = _w2 ( k l h )

_.

Step 3. Output

W ,

and stop.

where the fuzzy partitions of input linguistic variable 51 are “small,” “medium,” and “large.” The three rules R I , R2 and RJ can be merged to one rule as follows

R: IF 2 2 is small, THEN y is good.

That is, the input variable 5 1 is not necessary in this SitUa-

tion. The conditions for applying rule combination has been explored in [301 and are given as follows.

1) These rule nodes have exactly the same consequents. 2) Some preconditions are common to all the rule nodes,

that is, the rule nodes are associated with the same term nodes.

B. Structure Leurning Phase

In this subsection, we propose a structure learning algorithm for the proposed neural fuzzy system to reduce its node and link number. This structure learning algorithm is divided into two parts: One is to merge the fuzzy terms of input and output linguistic variables (term-node combination). The other is to do rule combination to reduce the number of rules. We shall discuss these two parts separately in the following.

LIN AND L U A NEURAL FUZZY SYSTEM WITH LINGUISTIC TEACHING SIGNALS

- \ U I U U

X I x2 x , X I x , x ,

Illustration of rule combination.

Fig. 5.

B

Input

Fig. 6. The membership functions of the input linguistic value “very small” (Xl), “small” ( X 2 ) , ‘‘large’’ ( X 3 ) in Example 1.

3) The union of other preconditions of these rule nodes composes the whole terms set of some input linguistic variables.

If some rule nodes satisfy these three conditions, then these rules can be combined into a single rule. Another example of rule combination is shown in Fig. 5.

The following simple examples illustrates the performance of the proposed supervised learning algorithm on the FCLO. One practical application of this technique is to do rule base concentration in fuzzy rule base. It can effectively find a small set of representative rules from a bunch of fuzzy if-then rules by removing redundancy and finding similarity. One practical example of rule base concentration will be given in Section VI. Example 1: Consider the following three fuzzy if-then rules for training

R I :

I F z is very small ( X l ) , THEN y is very large ( D l ) ,

Rz:

I F z is small (X2), THEN y is large (D2),

RJ:

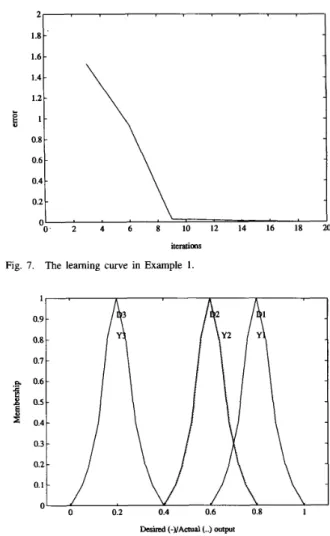
I F z is large (X3), THEN y is small (D3),

where the fuzzy numbers “small”, “large”, “very small” are given in Fig. 6. Because input and desired output are linguistic, an FCLO is used in this example. According to the initializa- tion process, we set up a FCLO with two layer-2 nodes and two layer-4 nodes (and thus two layer-3 (rule) nodes). Fig. 7 shows the learning curves. The error tolerance is 0.0001

and the number of a-cuts is 6. After supervised learning, the fuzzy outputs of the learned FCLO and the corresponding desired outputs are shown in Fig. 8. The figure shows that

they match closely. The two learned (representative) fuzzy

iterations

Fig. 7. The learning curve in Example 1.

Dsired (-l/Actual(..) output

Fig. 8. The actual fuzzy outputs, Y1, Y 2 , Y 3 of the learned neural fuzzy system and the corresponding desired fuzzy outputs, D l I D 2 , D 3 in Example

1.

rules after learning (condensing) are

IF z is WX1, THEN y is WY1,

IF z is WX2, THEN y is WY2 and

where the fuzzy weights after learning are shown in Fig. 9. For illustration, Figs. 10 and 11 show the change of fuzzy weights in the learning process. Hence the original three fuzzy rules have been condensed to two rules, and these two sets of fuzzy rules represent equivalent knowledge.

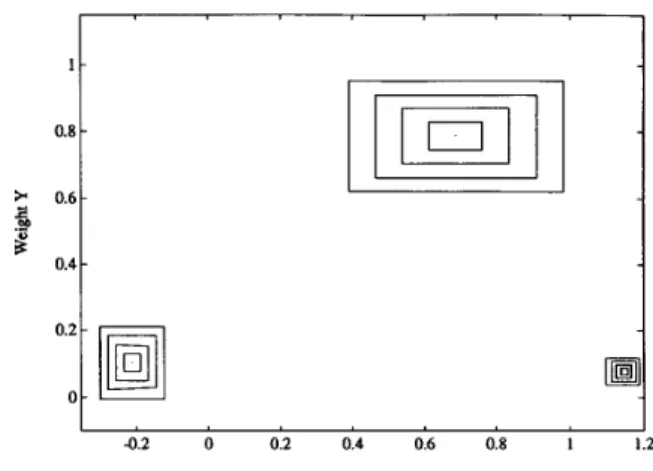
Example 2: In this exampie, we train an FCLO with five training fuzzy number pairs shown in Fig. 12. In this figure, the stacked rectangles represent different a-level sets. Five level sets corresponding to a = 0,0.25,0.5,0.75,1 are used for each fuzzy number. In the initial FCLO, there are four nodes in each of layers 2,3, and 4. That is, there are four fuzzy rules initially. After the structure and parameter learning, we obtain an FCLO containing three fuzzy rules (i.e., there are three nodes in each of layers 2, 3, and 4). Fig. 13 shows the learned fuzzy weights. To examine the generalization capability of the trained FCLO, we present three novel fuzzy numbers to its

178 1 - 0.8

*

3 0.6 0.4

A

0.2 0 -

IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3, NO. 2, MAY 1995

-

- - -

Weight X (-)/Weight Y (..)

Fig. 9. The learned fuzzy weights of the FCLO in Example 1.

The change in Weights WXl(..), WXZ(-)

Fig. 10. Time evolving graph of fuzzy weights W X I , W X 2 during the learning process in Example 1.

The change in Weights WYl(..), WYZ(-) Fig. 11.

learning process m Example 1.

Time evolving graph of fuzzy weights W Y 1 , WY2 during the

input nodes for testing. The results shown in Fig. 14 (the dashed rectangles) indicate the good generalization capability of the learned FCLO.

l a

0 0.2 0.4 0.6 0.8 1

Inputs x Fig. 12.

Example 2.

The training fuzzy pairs ( X , Y ) in the form of a-level sets in

1 - 0.8

-

0.6 -

s

’

0.4 - 4 . 2 0 0.2 0.4 0.6 0.8 I Weight X Fig. 13. The learned fuzzy weights in Example 2.

b

a 9 1 0.8 0.6 0.4 0.2 a 2 0 0.2 0.4 0.6 0.8 1

Inputs x for testing

Fig. 14. Generalization test of the learned neural fuzzy system in Example 2.

V. REINFORCEMENT LEARNING WITH FUZZY CRITIC SIGNAL

In the previous section, we considered the supervised learn- ing of the proposed neural fuzzy system and assumed that

LIN AND LU: A NEURAL FUZZY SYSTEM WITH LINGUISTIC TEACHING SIGNALS membership value

-1 0

Fig. 15. An example of fuzzy reinforcement signals.

the precise “target” output for each input pattern was always available; however, in some real-world applications, precise training data are usually difficult and expensive to obtain. In

this section, we extend the supervised learning of the pro- posed system to reinforcement learning. In the reinforcement learning problem, we get only evaluative feedback (called the reinforcement signal) from the environment. Because the reinforcement signal is only evaluative and not instructive, reinforcement learning is sometimes called “learning with a critic” as opposed to “learning with a teacher” in supervised learning.

Conventionally, the reinforcement signal is regarded as a real number. For example, the reinforcement signal, r ( t ) , can be one of the following forms: 1) a two-valued number,

~ ( t )

E {-l,O}, such that r ( t ) = 0 means “a reward” and r ( t ) = -1 means “a penalty”; 2) a multivalued dis- crete number in the range [-1, 01, for example,

~ ( t )

E {-1, -0.25, -0.5, -0.25,O) which corresponds to different degrees of reward or penalty; 3) a real number,

r ( t )

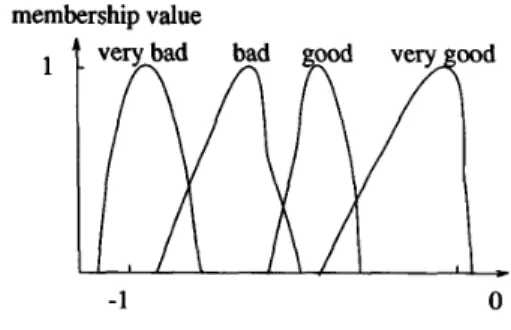
E [- 1,0], which represents a more detailed and continuous degrees of reward or penalty.

The reinforcement signal given by the external environment (e.g., an expert), however, may be fuzzy feedback information such as “good,” “very good,’’ “bad,” “too bad.” This is true especially in the human-iterative learning environment, where human instructor is available. We call the reinforcement learning problem with fuzzy critic feedback as the fuzzy reinforcement learning problem. In this section, we shall attack this problem by considering the reinforcement signal R(t) as a fuzzy number in the form of a-level sets. We also assume that

R(t)

is the fuzzy signal available at time step

t

and caused by the input and action chosen at time step t

-

1 or even affected by earlier inputs and actions. Namely, the reinforcement signal is a fuzzy number such that

where

-1

5

defuzzifier(R1)

5

defuzzifier(R2)

<

- e

. . 5

defuzzifier(R,)

5

0 (55)

where defuzzifier( R ( t ) ) represents discrete degree of reward or penalty. For example (see Fig. 15), we may have R ( t ) €(very bad, bad, good, very good).

In the reinforcement learning problems, it is common to think explicitly of a network functioning in an environment.

-

179

The environment supplies the inputs to the network, receives its output, and then provides the reinforcement signal. There are several different reinforcement learning problems, depend- ing on the nature of environment:

Class I: In the simplest case, the reinforcement signal is always the same for a given input-output pair. Thus there is a definite input-output mapping that the network must learn. Moreover, the reinforcement signals and input patterns do not depend on previous network outputs.

Class II: In a stochastic environment, a particular input- output pair determines only the probability of positive rein- forcement. This probability is fixed for each input-output pair and again the input sequence does not depend on past history. Class IIk In the most general case, the environment may itself be governed by a complicated dynamical process. Both reinforcement signals and input patterns may depend on the past history of the network outputs.

If a reinforcement signal indicates that a particular output is wrong, it gives no hint as to what the right answer should be; in terms of a cost function, there is no gradient information. It is therefore important in a reinforcement learning network for there to be some source of randomness in this network,

so that the space of possible outputs can be explored until a correct value is found. This is usually done by using stochastic units. Several approaches have been proposed for the above three different classes of reinforcement learning problems. Barto and Anandan [12] proposed the associative reward- penalty algorithm A R - P , which is applicable to Class I and

11 problems. Its essential ingredient is the stochastic output unit. Another approach to reinforcement learning involves modeling the environment with an auxiliary network, which can then be used to produce a target for each output of the main network 1171, [35], [36]. This scheme reduces the reinforcement learning problem to a two-stage supervised learning problem with known targets. This approach can be used to resolve reinforcement learning problems of Class I and 11, and the general idea of this separate modeling network can be also applied to Class 111 problems. Another approach aiming at solving Class 111 reinforcement learning problems is “learning with predictor.” In Class III problems, a reinforcement signal may only be available at a time long after a sequence of actions has occurred. To solve the long time-delay problem, prediction capabilities are necessary in a reinforcement learning system. In this scheme, a predictor (critic) receives the raw reinforcement signal T from the environment and feeds a processed signal ? on to the main network. The i signal represents an evaluation of the current behavior of the main network, whereas T typically involves

the past history. Recently, more and more researchers devote the reinforcement learning problems using this method [lo], [12]-[15]. In this paper, we also use this scheme in our

reinforcement learning model.

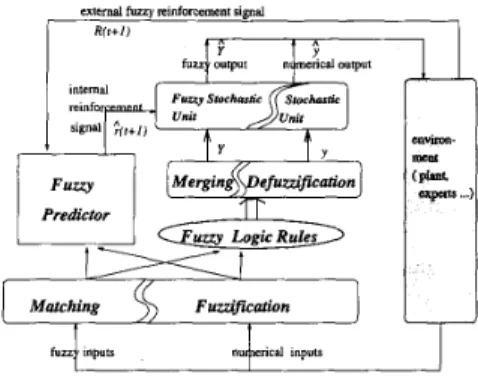
A. Architecture of Reinforcement Learning Model

The proposed reinforcement learning model, as shown in Fig. 16, integrates two previously proposed five-layered net- works (FCLOs or FCNOs developed in Section 111) into a

180 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3, NO. 2, MAY 1995

Predictor

Fig. 16. The proposed fuzzy reinforcement learning system.

learning system. One (FCLO or FCNO) serving as the action network can choose a proper action or decision according to the current input. The action network acts as a fuzzy controller. The other (FCLO) serving as the evaluation network performs single or multistep prediction of the external fuzzy reinforcement signal. The evaluation network acts as a fuzzy predictor. The fuzzy predictor provides the action network with more informative and beforehand internal reinforcement signal for learning. Because the reinforcement signal is a fuzzy number, an FCLO is used for fuzzy predictor. The action network can be FCLO or FCNO depending on the actual requirement. Structurally, these two networks share the first two layers of the original FCNO or FCLO (see Fig. 16). This means that they partition the input space in the same way.

We distinguish two kinds of prediction-learning problems for the fuzzy predictor. In the single-step prediction problems, all information about the correctness of each prediction is revealed at once. In the multistep prediction problems, cor- rectness is not revealed until more than one time step after the prediction is made, but partial information relevant to its correctness may be revealed at each time step. In the single- step prediction problems, data naturally comes in observation- output pairs; these problems are ideally suited to the pairwise supervised learning approach. We shall discuss these problems in Subsection V-B. For the multistep prediction problems, we use the temporal difference (TD) prediction technique, which is a class of incremental learning procedures introduced by Sutton [ll]. The main characteristic of this technique is that they learn from successive predictions, whereas in supervised learning methods, learning occurs only when the difference between the predicted outcome and actual outcome is revealed. Hence the learning in TD does not have to wait until the actual outcome is known and can update its parameters at each time step. We shall explore these problems in our proposed model in Subsection V-C.

For the action network, the reinforcement learning algorithm allows its output nodes to perform stochastic exploration. With the internal fuzzy reinforcement signals from the fuzzy predictor, the output nodes of the action network can perform more effective stochastic searches with a higher probability of choosing a good action as well as discovering its output error accurately. The detailed learning procedure will be discussed in the following subsections.

In a word, the architecture of the proposed reinforcement learning model schematically shown in Fig. 16 has three components:

The action network maps a state vector into a recom- mended actions, Y or y, using FCLO or FCNO. The evaluation network (predictor) maps a state vector and an external fuzzy reinforcement signal into a pre- dicted fuzzy reinforcement signal which indicates state goodness. This is also used to produce internal reinforce- ment signal.

The stochastic unit using both Y (or y) F d the internal reinforcement signal to produce an action Y (or y), which is applied to the environment.

Since the action network and the evaluation network are in fact the FCLO or FCNO introduced in Section 111, their node operations in five layers are the same as those in the original structure. Let us now describe the operations in the stochastic unit in Fig. 16.

To estimate the gradient information of error function in a reinforcement learning network, there needs to be some source of randomness such that the space of possible output can be explored to find a correct value. Thus, the stochastic unit is necessary for the action network. In estimating the gradient information, the output Y(y) of the action network does not directly act on the environment. Instead, the stochastic unit uses the predicted fuzzy reinforcement signal P ( t ) of the evaluation network and the action Y(y) recommended by the action network to stochastically generate an attual action

Y

(5)

acting on the environment. The actual action Y

(9)

is a random variable with mean Y(y) and variance cr(t). The variance (or width) a ( t ) representing the amount of exploration is some nonnegative, monotonically decreasing function of P ( t ) . In our model, a ( t ) is chosen as

(56)

2k

a ( t ) = ~ -

k,

1

+

e X P ( t )

p ( t ) = defuzzifier(P(t)) (57)

where X is a search-range scaling constant which can be simply set to 1, and P ( t ) is the predicted fuzzy reinforcement signal used to predict R(

t

+

1) when the environment state is X (t) or

z ( t ) .

The magnitude of

a ( t )

is large when p ( t ) is low. Because we restrict the highest degree of reward to p ( t ) = 0, the value

of a ( t ) is 0 whenp(t) = 0. The action

Y,

or y, is what actually applied to the environment. The stochastic perturbation in the suggested approach leads to a better exploration of action space and better generalization ability.

Once the amount of exploration, cr( t), has been decided, the next problem is how to generate the actual output. Because the output of the learning system can be fuzzy number or numerical number, we discuss these two situations separately in the followings.

I) Numerical Stochastic Unit: When the action is a numer- ical value y (i.e., a FCNO is used as the action network), the actual output

6

of the stochastic unit can be set as

181

LIN AND L U A NEURAL FUZZY SYSTEM WITH LINGUISTIC TEACHING SIGNALS

membership grade

7

Y

t

y d search rangle

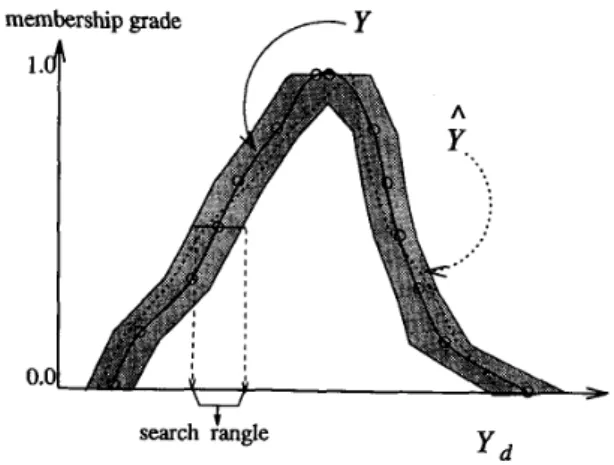
Fig. 17. Illustration of fuzzy stochastic exploration.

That is,

$(t)

is a normal or Gaussian random variable with variance o(t), mean y(t), and the density function

(59) The actual output y can be also set simply as a uniform random variable with width 20, mean y, and the density function

(60)

-,

if (y - 0)

I

Y

I

(y

+

a ) ,

f(Y) = 2a

{ l 0, otherwise.

2 ) Fuzzy Stochastic Unit: When the action is a fuzzy num- ber Y = U, a[y?),yp’] (i.e., a FCLO is used as the action network), the fuzzy stochastic unit generates a fuzzy action, Y = U, a[$?),

$?)I,

based on the amount of exploration a. The parameter

$p)(yp))

is set as a uniform random variable with mean y p ) ( y p ) ) , width 20, and the density function as the same as above. After having decided these parameters, yp’

and yp), we must then maintain the convex property of the

fuzzy action. We propose the following procedure to complete the fuzzy stochastic exploration. In this procedure, the notation

h is the number of quantized membership grade. As shown in

Fig. 17, the actual fuzzy action Y must falls in the shadow region randomly in the fuzzy stochastic exploration.

Procedure: Fuzzy Stochastic Exploration: Input: Y = ~ , a [ y ~ ) , y ~ ) l . output: Y =

U”a[yp),gp)].

Step 1. For

k

= 1 to h, find

$ik)

such that

Step 3. Output Y and stop.

Like the supervised learning process introduced in Section IV, we need to perform two kinds of initialization: structure initialization and parameter initialization before performing the reinforcement learning algorithm. The initialization process is exactly the same as that for the supervised learning (see Section IV). It should be done on both the action network and the evaluation network. After the initialization process, the reinforcement learning algorithms are performed on both networks. These learning algorithms for both the action net- work and the evaluation network are derived below. Again, we discuss the single step and multistep prediction problems separately in the following subsections.

B. Leaming Algorithm for Single-Step Prediction Problems In this subsection, a reinforcement learning algorithm is proposed to solve the Class I and Class

II

reinforcement learning problems described previously using a single-step fuzzy predictor. The function of the single-step fuzzy predictor is to predict the external fuzzy reinforcement signal, R(t

+

1)

,

one time step ahead, that is, at time t. Here,

R(t

+

1) is the external fuzzy reinforcement signal resulting from the inputs and actions chosen at time step

t ,

but it can only be known at time step

t

+

1. If the fuzzy predictor can produce a fuzzy signal P ( t ) at time step

t ,

which is the prediction of R(t

+

l), a better action can be chosen by the action network at time step

t ,

and the corresponding learning can be performed in the action network at time step

t

+

1 upon receiving the external reinforcement signal R(t

+

1).

Basically, the reinforcement learning of a single-step fuzzy predictor is simply a supervised learning problem. The goal is to minimize the squared error

e =

+

C [ ( p p ) ( t )

- r p ) ( t

+

1>>2

LI

+

(p?’(t) -

r p ( t

+

1))2] (61)

where R(t

+

1) = U,a[rp)(t

+

l ) , r ? ) ( t

+

l)] represents the desired fuzzy output, and P ( t ) = U,a[pp’(t),p?)(t)] is the current predictor output. Similar to the supervised learning algorithm developed for FCLO in Subsection IV-A, we can derive the learning algorithm for the single-step fuzzy predictor. The update rules are the same as (33)-(53) if Y is replaced by P ( t ) and

D

is replaced by

R(t

+

1).

We next develop the learning algorithm for the action network. The goal of the reinforcement learning algorithm is to adjust the parameters wp’ and wp) of the action network such that the fuzzy reinforcement signal R is maximum; that is

d r A W N -

dW

where w =

wp)

or

wp)

and r = defuzzifier(R). There are two different reinforcement learning algorithms for the action network depending on either FCNO or FCLO being used as the action network. We describe these two reinforcement learning algorithms for the action network in the followings.

182 IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 3, NO. 2, MAY 1995

numerical A

-

when p (

t )

#

r(

t

+

1). Then we can define the error function as

output

Y

Y

Y

- _ - - - - _ _ _ _ _

V , V n v e =

c[(yp'

-

S',-')2

+

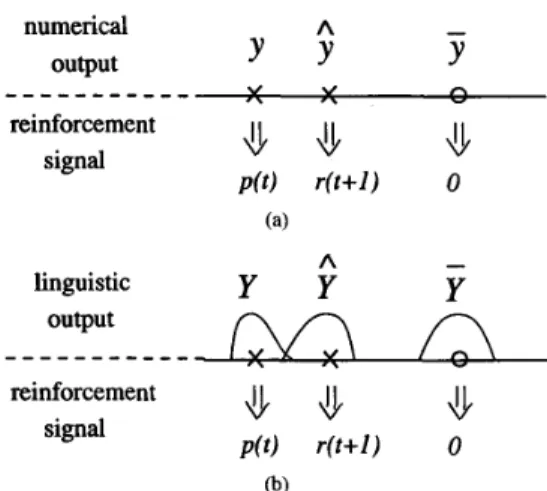
( y p ) - jjp')']. (67) reinforcement signal

4

r ( t + l )

4

0 (b)

Fig. 18. The concept of deciding desired outputs in the stochastic unit.

We first derive the reinforcement learning algorithm for the action network with numerical output (FCNO). In this situation, to determine d r l d w , we need to know d r l d y , where y is the output of the action network. Since the fuzzy reinforcement signal does not provide any hint as to what the right answer should be in terms of a cost function, the gradient,

d r l d y , can only be estimated using the stochastic unit.

The output of the single-step predictor, P ( t ) , is a predicted fuzzy reinforcement signal for the output of the action network, y(t), and the external fuzzy signal R(t

+

1) is a critic score from environment for actual output y(t) of the stochastic unit. From these values, we can construct a desired target output

jj(t).

Note that we restrict the values of defuzzified reinforcement signals, P ( t ) and

R(t

+

I)

,

in the range

[

- 1, 0]

,

that is, -1

5

p ( t )

5

0 and -1

5

r ( t

+

1)

5

0, where

p ( t ) = defuzzifier(P(t)) and r ( t + l ) = defuzzifier(R(t+l)). From Fig. 18, we find that the expected target output

g

should fall on the position representing that the value of reinforcement signal is 0. Hence, if p ( t )

#

r ( t

+

l ) , we let

Then, if p ( t )

#

r ( t

+

l), we can define

e = +(y - iJ2. (64)

When p ( t ) =

~ ( t

+

l ) , the weights are not changed, that is, d e l a y = 0. With this error function, the learning rules of the FCNO-based action network can be derived. They are the same as (33)-(53) if d is replaced by ij.

When the output of the action network is a fuzzy number Y , we can derive the learning algorithm in a similar way as we did in the above. We decide an expected fuzzy target output

Y =

u,a[g',-',~p)]

as -

a

When p ( t ) = r ( t

+

l ) , the weights are not changed, that is, d e l d y p ) = 0 and d e / d y p ) = 0. With this error function, the learning equations of the FCLO-based action network are the same as (33)-(53) if

D

is replaced by

L.

There is another method to estimate the gradient information [lo]. This method does not construct the expected target output, but finds the gradient direction of the error function. With this method, the output error gradient in (33)-(53) for FCNO can be replaced by

and for FCLO, the gradient information is estimated by

where

1'

is the internal reinforcement signal sent to the action network. In (68), r ( t

+

1) is the actual fuzzy reinforcement feedback for the actual action,

jj(t),

and p ( t ) is the predicted fuzzy reinforcement signal for the expected action, y(t). The ratiole behind the above equations is described as follows. If

r ( t

+

1)

>

p ( t ) , then y(t) is a better action than the expected one, y(t), and y(t) should be moved closer to

jj(t).

That is, this is a rewarding event when F ( t + 1)

>

0. If

r ( t +

1) < p ( t ) ,

then y(t) is a worse action than the expected one, and y(t) should be moved farther away from y(t). That is, this is a penalizing event when 1'(t

+

1)

<

0.

In the proposed system, the action network and the evalu- ation network are trained together, however, since the action network relies on accurate prediction of the evaluation net- work, it seems practical to train the fuzzy predictor first, at least partially, or to let the fuzzy predictor have a higher learning rate than the action network. Besides the above pa- rameter learning phase, the structure learning phase described in Section IV is executed to complete the whole learning process.

C. Leaming Algorithm f o r Multistep Prediction Problems The algorithms described in the last subsection work under the assumption that the environment returns a fuzzy reinforce- ment signal in response to every single action acting on it. There are many applications in which the learning system receives evaluation of its behavior only after a long sequence of actions; that is, both reinforcement signals and environment states may depend arbitrarily on the past history of the network output. This kind of reinforcement scheme is called delayed reinforcement. In this section we shall discuss how the problem of learning with delayed reinforcement can be solved using the multistep fuzzy predictor.