The beta-assignment problem in general graphs

Pergamon

Computers Ops Res. Vol. 24, No. 8, pp, 757-765, 1997 © 1997 Elsevier Science Ltd All rights reserved. Printed in Great Britain 0305-0548/97 $17.00+0.00

T H E / 3 - A S S I G N M E N T P R O B L E M 1N G E N E R A L G R A P H S Gerard J. Chang~t:~ and Pei-Hsin Ho2§

J Department of Applied Mathematics, National Chiao Tung University, Hsinchu 30050, Taiwan 2 Intel Corporation, 2111 N.E. 25th Avenue, JFT- 102, Hillsboro, OR 97124, U.S.A.

(Received July 1996; in revised form October 1996)

Scope and Purpose---The purpose of this paper is to study a variant assignment problem in operations research. Suppose we have a set of jobs and a set of workers. The qualifications of workers for each job are known in advance. The problem is to assign the jobs to the workers so that the maximum number of jobs a worker has to perform is minimized. If there are pairs of jobs that can help each other, we can assign them in symbiotic pairs without assigning them to workers. The fact that two jobs can help each other is also a known. This paper studies this general problem from an algorithmic point of view.

Abstract--We study a variation of the assignment problem in operations research and formulate it in terms of graphs as follows. Suppose G=(V,E) is a graph and U a subset of V. A/~-assignment of G with respect to U is an edge set X such that degx(v)= 1 for all vertices v in U, where degx(v) is the degree of v in the subgraph of G induced by the edge set X. The ~-assignment problem is to find a ~-assignment X such that ~(X)~max

{degx(v):vEV-U} is minimum. The purpose of this paper is to give an O(n3)-time algorithm for the ~- assignment problem in general graphs. As byproducts, we also obtain a duality theorem as well as a necessary and sufficient condition for the existence of a /~-assignment for a general graph. The latter result is a generalization of Tutte's theorem for the existence of a perfect matching of a general graph. © 1997 Elsevier Science Ltd

1. I N T R O D U C T I O N

The assignment problem is a well-known subject in operations research [1-5]. Chang and Lee [6] considered the following variation of the assignment problem. There is a set S of n jobs and a set of T of m workers. A worker's qualifications for a given job are known. The problem is to assign jobs to workers so that the maximum number of jobs a worker has to perform is optimized. The problem was formulated as follows in terms of bipartite graphs. Consider the bipartite graph G=(S,T,E) in which (S,T) is a bipartition of the vertex set, and (ij) ~ E if and only if worker j is qualified for job i. The problem is then to find an edge subset X of E such that degx(v)= 1 for all vertices v in S and max {degx(v):v ~ T} is as small as possible, where degx(v) is the degree of v in the subgraph of G induced by X.

This paper studies the following variation of the above assignment problem. In this variation, there are pairs of jobs that can help each other so that we do not need to assign them to workers. The fact that two jobs can help each other is also a known. The problem is formulated in terms of graphs as follows. Suppose G=(V,E) is a graph and U a subset of V. A ~assignment of G with respect to U is an edge set X such that degx,(v) = 1 for all vertices v in U. The ~assignment problem is to find a ~assignment X such that ~X)~max{degx(v):ve V - U} is minimum. Note that in the case of G as a bipartite graph (S,T,E), we choose U=S. In the case of a general graph G=(V,E), an edge (x,y) with x and y in U means the jobs x and y can help each other. Note that we may assume a ~assignment X contains no edge (z,w) with z and w in V - U, since the deletion of such an edge from X never increases the value/~(G).

Figure 1 shows an example of a graph with 12 vertices, in which the circled vertices form the job set U= { 1, 2, 3, 4, 7, 9, 10, 11, 12} and the squared vertices form the worker set V - U= {5, 6, 8}. The bold edges in Fig. 1 (b) form a ~assignment Y of G with respect to U. In this case, jobs 1 and 2 help each other and need not be assigned to any worker, job 3 is assigned to worker 6, jobs 4 and 7 help each other, jobs 9 and 10 are assigned to worker 8, and jobs 11 and 12 help each other. Since the maximum number of jobs a worker is assigned is two, we have ~(Y)=2. Note that Y ' = Y - {(5,6)} is also a/3-assignment with

"t To whom all correspondence should be addressed (emaih gjchang@math.nctu,edu.tw).

C~rard J. Charlg received his B.S. degree in Mathematics from National Central University and Ph.D. in Operations Research from Cornell University (1982). He is a professor of the Department of Applied Mathematics at National Chiao Tung University. His research interests include combinatorial optimization, graph algorithms and communication networks. § Pei-Hsin Ho received a B.S. degree in Mathematics from Chung-Yuan Christian University, an M.S. degree in Applied

Mathematics from National Chiao Tung University, and M.S. and Ph.D. degrees in Computer Science from Cot'nell University. He is a researcher at Strategic CAD Technology, lntel Development Labs. His research interests include formal verification and graph algorithms.

758 Gerard J. Chang and Pei-Hsin Ho

(a)

X = {(2,41,(3,6),(5,6),(S,9),(8,10),(11,12)}

(b)

Y ---- {(I, 2), (3, 6), (4, 7), (5, 6), (8,9), (8,10), (II, 12)}

circled vertices: job set U = {1,2, 3, 4, 7, 9, 10, 11, 12}; squared vertices: worker set V - U = {5, 6, 8}

Fig. I. A graph with 12 vertices.

~Y')=~(IO=2.

Chang and Lee [6] gave an O(n4)-time algorithm for the ~assignment problem in bipartite graphs. Chang [7] gave an O(n4)-time algorithm for the weighted ~-assignment in bipartite graphs. Chang and Ho [8] improved the above results by applying Hungarian-type algorithms for the cardinality, bottleneck and weighted ~-assignment problems in bipartite graphs. The running times of these algorithms are all O(n3). The main purpose of this paper is to give an O(n3)-time algorithm for the/3-assignment problem in general graphs. As byproducts, we obtain a duality theorem as well as a necessary and sufficient condition for the existence of a ~-assignment for a general graph. The latter result is a generalization of Tutte's theorem [9] for the existence of a perfect matching of a general graph.

2. T H E A L G O R I T H M

This section gives an O(n3)-time algorithm for the B-assignment problem in general graphs. This algorithm shares the same significance as the algorithms for the matching problem in general graphs [ 10--14]. We start this section with some basic definitions.

For a given graph G=(V,E) and a subset U of V, a partial ~assignment of G with respect to U is an edge subset X of E such that degx(v)-<l for all vertices v in U. For a partial ~-assignment X, a vertex i in U is exposed if degx(i) = 0, a vertex j in V - U is safe if degx(j) < fl(X), and any other vertex is saturated. We also call X a partial t-assignment of S, where S is the set of all nonexposed vertices in U. Figure 1 (a) shows a partial t-assignment X with fl(X)=2, in which 1 and 7 are exposed, 5 is safe, and all other vertices are saturated.

A walk or Vo-vr walk is a sequence (vo,v ~ ... Vr) of vertices such that (vi-,, vl) is an edge for l<-i<-r; where v 0 is called the origin and v, the terminus of the walk. A trail (respectively, path) is a walk with no repeated edges (respectively, vertices). Note that a path is always a trail, but the converse is not so. An X-alternating trail (respectively, path) is a trail (respectively, path) (Vo,V, ... v~) such that one of the set { (v~_ i, vi): 1-<i <- r and i is odd} and {(v~_ ,, v~): 1 <-i<-r and i is even} is a subset of E - X and the other a subset of X. An X-augmenting trail (respectively, path) is an X-alternating trail (respectively, path) whose origin x is an exposed vertex in U and whose terminus y is exposed in U or safe in V - U when the trail (path) is of odd length, and y is in V - U when the trail (path) is of even length. In Fig. l(a), Pl=(1, 2, 4, 7), P2=(1, 2, 4, 5), and P3=(1, 2, 4, 5, 6, 9, 8) are X-augmenting paths; P4=(1, 2, 4, 8, 9, 12, 11, 10, 8) and Ps=(1, 2, 4, 8, 9, 12, 11, 10, 8, 7) are X-augmenting trails. Note that Pj and P5 are of odd length with terminus 7 exposed in U, P2 is of odd length with terminus 5 'safe in V - U, and

P3

Note that in the following contents we sometimes use 'trail' and at other times use 'path' on purpose. The first reason for using 'trail' is that a blossom is an X-alternating trail. The second reason is that in Lemma 2.2, an X-augmenting trail may exist when there is a blossom. So, in Lemmas 2.1 and 2.3, we n e l l to deal with X-augmenting trails. In fact, in this paper, the only X-augmenting trails that are not paths contain only a vertex that is repeated twice.

An easy argument proves the following lemma. The symmetric difference between two sets A and B, denoted by AAB, is (A - B) t.J ( B - A).

The fl-assignment problem 759 Lemma 2.1. If X is a partial fl-assignment of S and P an X-augmenting trail starting at vertex i ~ U - S,

then XAP is a partial fl-assignment of S'D_S O {i} and fl(XAP)<--I~(X).

As an example, in Fig. 1, X is a partial fl-assignment and Y=XzlPI is a/3-assignment such that f l ( Y ) = ~ X ) = 2 , where PI =(1, 2, 4, 7).

For a partial fl-assignment X of G with respect to U, an X-alternating tree is a rooted tree whose root is an exposed vertex in U and any path from that root to a vertex in the tree is an X-alternating path.

Suppose that X is a partial fl-assignment of G with respect to U. A blossom B of G is an X-alternating trail of odd length that starts and ends at a same vertex b, which is also a unique vertex in B such that the X-alternating trail traverses it twice. We call b the base of the blossom. If there exists an X-alternating path P that starts at an exposed vertex r ~ U and terminates at b such that V(P)tq V(B)={b}, and the concatenation of P and B is still an X-alternating trail, then we call P the stem of the blossom and r the root of the blossom. Note that for the case in which P contains exactly one vertex, the root r is the same as the base b. The first and the last edges of a blossom B are either both in X or both not in X, since B is of odd length. In the case in which the base b of B is in U, these two edges must both be not in X, otherwise degx(b)---2 is a contradiction. In Fig. l(a), (4, 5, 6, 9, 8, 4) is a blossom with base 4, stem (1, 2, 4), and root 1; (8, 9, 12, 11, 10, 8) is a blossom with base 8, stem (1, 2, 4, 8), and root 1; (7, 4, 2, 3, 6, 9, 8, 7) is a blossom with base 7, stem (7), and root 7.

Lemma 2.2, Suppose B is a blossom with root r and base b. l f B contains a vertex t in V - U, then there

exists an X-augmenting trail starting at r.

Proof. Two X-alternating trails always exist in B from b to t of even and odd lengths, respectively; i.e. the clockwise and counterclockwise traversals of B. The concatenation of the stem P and one appropriate X-alternating trail is an X-alternating trail of even length from r to t. By definition, it is an X-augmenting trail starting at r. QED.

Remark. When t~r, the X-augmenting trail in the above lemma is in fact a path. The trail is not a path only when t=b. In this case, t is the only vertex that appears twice in the trail.

Now we are ready to describe our algorithm for the fl-assignment problem in general graphs. The algorithm begins with an empty partial fl-assignment. Suppose the partial/3-assignment X we have so far is not a fl-assignment. An exposed vertex r in U is taken as the root of an X-alternating tree and vertices and edges are added to the tree by means of a labeling technique. In other words, we say that a vertex i is in the X-alternating tree if it is labeled as 'S:f(i)' or 'T.3f(i)'; we also say that i has an S-label or T-label, respectively. We start by labeling the root r as 'S:$'. At each iteration, we scan a labeled but unscanned vertex i and process its neighbors as follows.

Suppose i has an S-label. For any vertex j with (i,j)E E - X , consider the following cases. For the case in whichj is unlabeled, we consider two subcases. I f j is a nonexposed vertex in U or a saturated vertex in V - U, label j as 'T:i'. I f j is an exposed vertex in U or a safe vertex in V - U, an X-augmenting path has been detected. We can obtain the inverse of this path by backtracking f r o m j using labels, i.e. J, f0), flflJ)),./(]~f0"))) ... r. For the case in which j has an S-label, a blossom has been detected. We backtrack from i and j, as above, to obtain two X-alternating paths P~ and P2 from r to i and j, respectively. Thus a path P exists such that PI=PPI ', P2=PPI ', and P~' intersects P2' at their origin b, which is also the terminus of P, So, P~'(ij)P2" is a blossom with base and stem P, where P2" is the inverse of P2'. For the case in whichj has a T-label, nothing need be done.

Suppose i has a T-label. For any vertex j with (id)¢X, consider the following cases. For the case in which j is unlabeled and in U, labelj as 'S:i'. For the case in whichj is unlabeled and in V - U, we can find an X-augmenting path from i to j as above. For the case in which j has a T-label, we can form a blossom containing (id) as above. For the case in whichj has an S-label, we do nothing.

Whenever a blossom B is found, we check whether it contains a vertex t in V - U. If this is the case, there exists an X-augmenting trail by Lemma 2.2, On the other hand, suppose all vertices of the blossom are in U. Neither the first nor the last edges of B are in X. Consequently, the base b has an S-label. In this case, we 'shrink' the blossom B, i.e. identify all vertices of B in G as a vertex s to form GIB. In other words, G/B is defined as (V',E') such that V ' = V - V ( B ) + s and E'=E-{(u,v):u or v~V(B)}+(u, s):(u,v)eE and v e B , but uqtB}. The vertex s in G/B corresponding to B is called a pseudo vertex, and is given the same label as the base of the blossom for the purpose of further tree construction. Note that

760 Gerard J. Chang and Pei-Hsin I-Io blossoms may be shrunken within blossoms to a depth of several levels.

If an augmenting trail is found in the X-alternating tree at some time, there is an X-augmenting trail in the original graph G. The existence of such a trail is proven by repeatedly applying Lemma 2.3. Lemma 2.3, Let B be a blossom with respect to X in G and X' = X - E( B). If there exists an X'-augmenting

trail P in GIB, then there exists an X-augmenting trail in G.

Proof. If P does not pass through the pseudo vertex s corresponding to B, then P is also an X- augmenting trail in G. If P passes through the pseudo vertex s, then P is of the form P~(u,s)(s,v)P2 or (s,v)P2, where PI and P2 are X-alternating trails. Since s has an S-label in G/B, (u,s) • X and (s,v) ~tX. Since all vertices in the shrunken blossom B are in U, u is adjacent to the base b of B in G, i.e. (u,b)eE(G). Suppose that t • V(B) is such that (t,v) • E(G). There is always an X-alternating trail PB from b to t of even length. Thus, either Pl(u,b)PB(t,v)P 2 or PB(t,v)P2 is an X-augmenting trail in G. QED.

Therefore, whenever an X-augmenting trail is found in our labeling procedure, we expand all blossoms within it to obtain an X-~iugmenting trail P in G. W can then augment X to XAP, and start a new iteration of the algorithm.

When it is impossible to add more labeled vertices or edges into the X-alternating tree L, we call L a Hungarian tree. If any vertex t e L A ( V - U) exists, then t is saturated and has a T-label. In this case we backtrack to obtain an X-alternating path of odd length from t to r. As in the case of an X-augmenting path, we expand the blossoms, if necessary, to create an X-alternating trail of odd length from t to r in the original graph G. Because we have no other better choice, we replace X with XAP and thus the value of fl(X) is increased by one. In the case of L A ( V - U) = ~b, we will prove that G has no t-assignment with respect to U. The tree-building procedure is repeated for at most IU1 iterations until an optimum/3- assignment with respect to U has been obtained or at some iteration we may conclude that G has no t-assignment with respect to U. More precisely, we have the following algorithm. An example is illustrated in Figs 2--4.

Algorithm Beta-Assignment ( G, U)

X,--~b; k,---0;

for each exposed vertex r e U do 1 label r with 'S:~b';

(*) find a labeled but unscanned vertex i • V and scan it as follows; if no such vertex i then {

case 1. there is a labeled vertex j • V - U:

backtrack f r o m j to r using labels to get an X-alternating path P; expand blossoms in it; X,---XAP; k,---k+ 1; goto Next-Iteration;

2 case 2. all labeled vertices are in U or are pseudo vertices: G has no t-assignment with respect to U; halt }; if i has an S-label then {for each (ij)~tX do

A H u n g a r i ~ ~ ~[ 1 / Initially Xo = ~ and/~(Xo) = 0.

There is an Xl-augmenting path Po = (12, 13).

Augment Xo using Po to get X1 with/~(X1) = 1. Fig. 2. A graph of 18 vertices with {7, 13} being the set of workers.

The ,8-assignment problem 761

(Blossom B2)S:2

(Blossom BI)S:2

(a) r T" 1

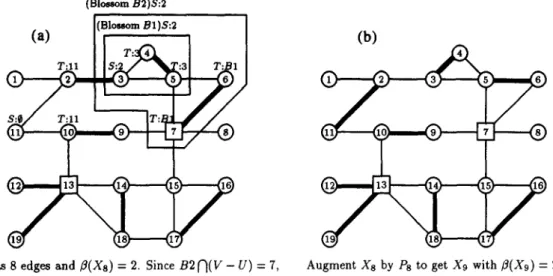
Xs has 8 edges and B(X8) = 2. S i n c e B 2 N ( V - U ) = 7 , Augment Xs by Ps to get Xg with B(X9) = 2. there exists an Xs-augmenting path/'8 = (11,2, 3, 4, 5, 6, 7).

Fig. 3. After eight iterations. case 1. j has a T-labeh do nothing;

case 2. j has an S-label: goto Blossom-Subroutine;

case 3. (j e U and j is exposed) o r (j E V - U and j is safe): goto A u g m e n t i n g - S u b r o u t i n e ; 3 case 4 . j is saturated or nonexposed: l a b e l j as 'T:i'; endfor};

if i has a T-label t h e n {for each (ij) e X do case 1. j has an S-label: do nothing;

case 2. j has a T-label: goto Blossom-Subroutine; c a ~ 3. j E V - U: goto A u g m e n t i n g - S u b r o u t i n e ; 4 case 4 . j e U: label j by 'S:i'; endfor};

goto (,);

N e x t . I t e r a t i o n : erase all vertex labels; end for;

o u t p u t (X,k); Blossom-Subroutine

{backtrack from i a n d j using labels until r is reached to find a blossom B; if B contains a vertex j e V - U

t h e n goto A u g m e n t i n g - S u b r o u t i n e ;

else {shrink B to a pseudo vertex; give the pseudo vertex the label of the base of B; leave it unscanned; goto (*); }

(a)

~

Hungarian Tree

S:7(B2)S::751

(b)

7

After backtraking from 13, we find an Xg-augmenting Augment X9 by P9 to get X10.

path/='9 - (13, 14, 18, 17, 16, 15, 7, 9, 10, 11, 2, I). Stop since there are no exposed vertices. Fig. 4. The final iteration.

762 Gerard J. Chang and Pei-Hsin Ho

T:I

OF = { ( D 's} Fig. 5. An odd family.

~:7 :15

Augmenting-Subroutine

{backtrack f r o m j using labels to r in order to find an X-augmenting path P; expand blossoms in it; X*-XAP; goto Next-Iteration;}

end Beta-Assignment.

3. C O R R E C T N E S S O F T H E A L G O R I T H M

We will prove the correctness of the algorithm with a primal-dual approach. As by-products of this proof, we also obtain a strong duality theorem as well as a necessary and sufficient condition for the existence of a #-assignment for a general graph. Since a perfect matching in G=(V, E) is precisely a #- assignment with respect to V, what we find is a generalization of Tutte's theorem for perfect matchings.

An oddfaraily (OF for short) is a family Ore= {VI,V2 ... V~,} of disjoint sets of vertices of U, such that each IV~I is odd and no vertex in V/is adjacent to a vertex in Vj when i#j. Figure 5 shows an example of an odd family. Denote as ~/,~ the set of vertices U

Iil~l

if there is no ambiguity] of W is { x e V - W : x is adjacent to some y e W } . The following lemma is a consequence of the definition of the odd family.

L e m m a 3.1. For any #-assignment X, there are at least ra vertices in 71~, that can only be assigned through X to vertices in N( *l.,).

Let X be a #-assignment of G with respect to U and let Ore= { Vt,V2 ... Vm} be an odd family. By Lemma 3.1, there are at least m vertices of 7/m, which Can only be assigned through X to vertices of N(r/m). Since r/~, f'IN(~_.~)= ~b, there are at least re=IN(r/m)n u1 vertices of r/m, which must be assigned to vertices of N(7/m) n u, where U = V - U. This implies that

I m - IN(r/i) n ol

I

v ~ vEN(,7.)nV IN(r/m ) n UI So we have the following min-max duality inequality.

Lemma 3.2.

m - IN(~/m) n r a i n ~ X ) > m a x _ ,

x : a - s ( ~ O.:OF I N ( ~ ) n U1 where f l - G(U) is a abbreviation of '#-assignment of G with respect to U'.

Note that Lemma 3.2 and the odd family in Fig. 5 permit us to conclude that the #-assignment Xt0 in Fig. 4(b) is an optimum #-assignment for the graph G in Figs 2-4. Denote as O; the odd family in Fig. 5. Then, ,/;= { 1,8,9,11,12,14,15,16,17,18,19}, N(~/;) f3 U= {(2,10}, and N(7/;) n u = {7,13}. According to Lemma 3.2,

The #-assignment problem 763

Im , ,oo117

I

3 =B(x~0)---B(G) > max -> _ =3.

o,,:or IN( n.) n ~ IN(n;) n uw

Therefore, the inequalities are actually equalities. This proves that Xto is an optimum #-assignment of G with respect to U and ~ G ) = 3 . We shall use the same idea to prove that the output of Algorithm Beta- Assignment is an optimum #-assignment.

Suppose L is a Hungarian tree at some iteration, and S and T are the sets of all vertices in the shrunken graph G* with S-labels and T-labels, respectively. We require the following lemma to show the correctness of our algorithm and that the inequality in Lemma 3.2 is in fact an equality.

L e m m a 3.3. The following statements are true.

(1) All vertices in a shrunken blossom are contained in U.

(2) Each vertex with an S-label in G* is either in U or is a pseudo vertex. A pseudo vertex always has an S-label.

(3) Every vertex, except the root r, with an S-label in G* is not exposed. (4) Every vertex with a T-label in G* is saturated or nonexposed. (5) N6. ( S A L ) = T A L .

(6) IfSnL={v~,v2 ... v,,}, then Om={Vi,V2 ... V,} is an odd family, where

f { }, Vi if is a vertex in G, Vi

Vi= I the set of vertices in the corresponding blossom, if v~ is a pseudo vertex.

(7) ISALI=ITfqLf-) 01+klTALA~Jl+ 1, where k=/~(X).

Proof.

(1)

(2) Any nonpseudo vertex is labeled as 'S:.' only at lines 1 or 4 of the algorithm. In any case, it is in U. On the other hand, suppose s is a pseudo vertex whose corresponding blossom is B. According to step (1), all vertices in B are in U. So neither the first nor the last edges of B are in X, otherwise degx(b)->2 for the base b of B. Consequently, b has an S-label and so does s. (3) The root r of L is clearly exposed in the algorithm. Suppose some vertex i, other than the root, has

an S-label. For the case in which i is not a pseudo vertex, i is labeled as 'S:*' only at line 4. This happens only when there is some j ~ U with (ij)~X. Hence i is nonexposed. For the case in which i is a pseudo vertex, the base of its corresponding blossom has an S-label according to step (2). According to the above argument, b is nonexposed and so is i.

(4) A vertex j is labeled as 'T.'.' only at line 3 of the algorithm, so j is nonexposed (respectively saturated) when it is in U (respectively V - U).

(5) In accordance with the algorithm, each vertexj adjacent to a vertex i of S-label via an edge ( i j ) ~ X is either in TA L or in S Iq L; and in the latter case, i andj detect a blossom, Then according to steps (1)-(3), every vertexj with an S-label is in U or is a pseudo vertex, and there is exactly one edge (id) in X, except when j is the root r. Using line 4 of the algorithm, i has a T-label. Hence NG,(SAL)CTf3L. Conversely, using line 3 of the algorithm, T A L C NG.(SAL). So, NG.(SfqL)=TrlL.

(6) Since the number of vertices in a blossom is odd, each IV~I is odd when we expand any blossom in a blossom or a pseudo vertex. Suppose i # j such that V~ has a vertex adjacent to some vertex in Vj. Then, v,. is adjacent to v i in the shrunken graph. As in the second line of the proof of step (5), (v~,vj) would detect a blossom and so must be shrunken into a vertex, which is a contradiction. So Om= { Vt,V2 ... V,,} is an odd family.

(7) Using step (5), T N L=N(S A L ). Using steps (2) and (3), each vertex j in S f'I L, except the root, is adjacentto exactly one vertex in TNL. With step (4), each vertex in T N L f ' ) U (respectively

T fq L A U) is adjacent to exactly one (respectively k) vertex in S fq T. So,

ISNLI=ITALA L~+klTf')LA 01+ 1. QED. Lemma 3.4. The following statements are equivalent.

764 Gerard J. Chang and Pei-Hsin Ho (1) G has a fl-assignment with respect to U.

(2) Algorithm Beta-Assignment does not halt at line 2.

(3) Algorithm Beta-Assignment outputs a/3-assignment X of G with respect to U.

Proof. (1)~(2). Suppose the algorithm halts at line 2. Let L* be the Hungarian tree at that moment, i.e. all vertices in L* are in U or are pseudo vertices. According to Lemma 3.3, steps (5)-(7), O~, is an odd family, ISnL*I=ITnL*I+ I, and N c. ( S n L * ) = T n L * . Using Lemma 3.1, in r/*, there are at least m vertices that can only be assigned through X* to vertices in N(r/~,)=NG. ( S n L * ) = T N L * . Yet IT n L*I <IS N L*I, at least two vertices of r/*,, must be assigned to the same vertex in T n L'C_ U, which is impossible. Thus, G has no fl-assignment with respect to U.

(2)~(3). It is clear that, after at most IU1 iterations, a/3-assignment X of G with respect to U together with ~ X ) is obtained by the algorithm.

(3)~(1). This is clear. QED.

Now, we are ready for simultaneous proof of the strong duality theorem and the validity of the algorithm.

Theorem 3.5. Algorithm Beta-Assignment works and the strong duality equality holds:

min ~ X ) = max

X:B- G(U) O=:OF

m - IN(r/.) n . IN(r/,,,) n

Proof. Suppose x:~i_'nto fl(X)=oo, i.e. G has no fl-assignment with respect to U. Lemma 3.4 shows that the algorithm does halt without returning any/3-assignment. Also, as in the proof of Lemma 3.4, there exists a Hungarian tree L* whose vertices are in U or are pseudo vertices such that S n L* produces an odd family O* with m*=ISOL*I=ITnL*I+ 1 and NG(r/m)=NG,(SOL*)=TnL*CU. Thus,

m* -IN(r/,'.) n t~ 1 IN(r/7.) n u1 = 6 =oo.

Therefore, the equality holds when G has no/3-assignment with respect to U.

On the other hand, suppose G has a/3-assignment. Using Lemma 3.4, the algorithm outputs (X*, k*). Let L* be a Hungarian tree that forces the k value to increase from k* - 1 to k*. Let O~, be the odd family produced by S O L * , as in Lemma 3.3, step (6). According to Lemma 3.3, step (5),

Nc.(S n L*) = TO L'and so NG(r/m) = T n L . Using Lemma 3.3, step (7),

m * = I S n L * I = I T n L * n Ul+(k* - 1)ITO L* O UI+ 1. Hence,

m* - IN('o~) n

IN(r/:)nu1

Therefore, the inequalities are equalities. This proves that X* is an optimum solution and the strong duality equality holds. QED.

By a similar argument, we have the following existence theorem for a g-assignment of a general graph.

Theorem 3.6. G=(V,E) has a B-assignment with respect to U if and only if O(G-D)<-IDI for all DC_U, where 0(0 - D) is the number of odd components contained in U of O - D.

Proof. Suppose there exists a subset DC_U such that O(G-D)>IDI. Consider the odd family Ore= { V~,V2 ... Vm} in which each V~ is an odd component contained in U of G - D. Then, N(r/m)C.D and

The B-assignment problem 765 so m= O ( G - D)IDI>-IN(Bm)I. Thus, G has no

#-assignment

according to

Conversely, suppose G has no fl-assignment with respect to U. According to Lemmas 3.3 and 3.4, there exists a Hungarian tree L* whose vertices are in U or are pseudo vertices such that S rl L* produces an odd family O,*, with m * = I S f ' ) L * I = I T N L * I + I and NG(rI,,)=Nc.(Sf')L*)=TNL*C_U. Since V/CU for each i, O(G - (Tf3L*))>-m*=IL * f') ~ + 1 >IL* f') 7]. QED.

As mentioned before, a perfect matching in G = ( E E ) is just a fl-assignment with respect to V. Thus, Theorem 3.6 is a generalization of Tutte's theorem for perfect matchings.

4. IMPLEMENTATION AND TIME COMPLEXITY OF THE ALGORITHM.

There are two principal elaborations required for Algorithm Beta-Assignment. First, it must detect and shrink blossoms. Second, it must be able to discover appropriate X-angmenting trails through shrunken blossoms. Edmonds [11] gave efficient implementations of these two operations for the matching algorithm. Although a matching is only a special/t-assignment with respect to U when U= V, Edmonds' implementations o f those two operations are still applicable to our algorithm since our algorithm shrinks blossoms that contain only vertices in U. According to Lawler's modification [4] of Edmonds' blossom procedure, the time complexity of those operations are listed as follows.

Our algorithm requires the following blossom operations: (1) blossom detecting; (2) blossom backtracking; (3) blossom checking (to see if the blossom is contained in U); (4) extra labeling of vertices in blossoms (applying missing labels to them); (5) blossom recording. The first operation needs O(1) time and the other operations can be done in O(n) time.

Our algorithm also requires the following augmenting trail operations: (1) X-augmenting trail detecting; (2) backtracking; (3) finding appropriate X-alternating trails through shrunken blossoms; (4) augmenting the partial B-assignment X. All of these operations require O(n) time, except for the first operation, which only needs constant time.

We can now consider the time complexity of our algorithm. In each tree-building iteration, we apply the labeling procedure to G. No more than O(n) blossoms in U are formed. Each blossom requires the shrinking operation, which needs O(n) time. There is at most one X-augmenting trail formed in each iteration. It requires O(n) time to backtrack the trail and augment X. Moreover, each application o f the labeling procedure scans at most O(n) labeled but not scanned vertices, and each scanning operation requires at most O(n) steps. Hence, simple scanning and labeling operations contribute O(n 2) steps per iteration. Since there are no more than O(IUI) iterations, we can conclude that the overall running time of Algorithm B e t a - A s s i g n m e n t is O(n 3).

Acknowledgements--The authors thank the referees for their many useful suggestions in revising this paper. This study was supported in part by the National Science Council under grant NSC77-0208-M009-21.

REFERENCES

I. Balinski, M. L. and Gomory, R. E., A primal method for the assignment and transportation problems. Management Science, 1964, 10, 578-593.

2. Kuhn, H. W., The Hungarian method for the assignment problems. Naval Research and Logistics Quarterly, 1955, 2, 83-97. 3. Kuhn, H. W., Variants of the Hungarian methods for assignment problems. Naval Research and Logistics Quarterly, 1956, 3,

235-258.

4. Lawler, E. L., Combinatorial Optimization: Networks and Matroids. Holt, Rinehart and Winston, New York, 1976. 5. Papadimitriou, C. H., Combinational Optimization: Algorithms and Complexity. Prentice-Hall, Englewood Cliffs, NJ, 1982. 6. Chang, R. S. and Lee, R. C. T., On a scheduling problem where a job can be executed only by a limited number of processors.

Computers and Operation Research, 1988, 15, 471-478.

7. Chang, R. S., A weighted job assignment problem and #P-complete result. Proc, 3rd Int. Conf. for Young Computer Scientists, Beijing, 15-17 July 1993.

8. Chang, G. J. and Ho, E-H., The fl-assignment problems, European Journal of Operations Research, to appear. 9. Tutte, W. T., The factorization of linear graphs. Journal of the London Mathematical Society, 1947, 22, 107-111. 10. Balinski, M. L., Labeling to obtain a maximum matching. Mimeographed paper, 1967.

11. Edmonds, J., Paths, trees and flowers. Canadian Journal of Mathematics, 1965, 17, 449--467.

12. Edmonds, J., An introduction to matching. Mimeographed notes, Engineering Summer Conf., The University of Michigan, Ann Arbor, MI, 1967.

13. Even, S. and Kariv, O., An O(n 2.~) algorithm for maximum matching in general graphs. Proceedings of 16th Annual Symposium

on Foundations of Computer Science, IF, EE, New York, pp. 100-112, 1975.

14. Micali, S. and Vazirani, V. V., An O(IVl°-~lEI) algorithm for finding maximum matching in general graphs. Proceedings of 21st

Annual Symposium on Foundations of Computer Science, Berkeley, Long Beach, IEEE, pp. 17-27, 1980. 15. Bondy, J. A. and Murty, U. S. R., Graph Theory With Applications. University Press, Belfast, 1976. 16. Lov(tsz, L. and Plummet, M. D., Matching Theory. North-Holland, Amsterdam, 1986.