Hybrid Compensation Control for Affine
TSK Fuzzy Control Systems
Chih-Ching Hsiao, Shun-Feng Su, Member, IEEE, Tsu-Tian Lee, Fellow, IEEE, and Chen-Chia Chuang
Abstract—The paper proposes a way of designing state feedback
controllers for affine Takagi-Sugeno-Kang (TSK) fuzzy models. In the approach, by combining two different control design method-ologies, the proposed controller is designed to compensate all rules so that the desired control performance can appear in the overall system. Our approach treats all fuzzy rules as variations of a nom-inal rule and such variations are individually dealt with in a Lya-punov sense. Previous approaches have proposed a similar idea but the variations are dealt with as a whole in a robust control sense. As a consequence, when fuzzy rules are distributed in a wide range, the stability conditions may not be satisfied. In addition, the con-trol performance of the closed-loop system cannot be anticipated in those approaches. Various examples were conducted in our study to demonstrate the effectiveness of the proposed control design ap-proach. All results illustrate good control performances as desired.
Index Terms—Affine TSK fuzzy model, fuzzy control, hybrid
compensation control.
I. INTRODUCTION
T
HE STUDY of stable analysis and control design for fuzzy systems has attracted many researchers recently. In the control design study, there are two types of control design prob-lems found in the literature. The first one is to design a fuzzy controller for a nonlinear or unknown system, and the other is to find a controller for a fuzzy system. In the former case, a so-called adaptive fuzzy control is usually used. Generally, the basic objective of adaptive control is to maintain consis-tent control performance in the presence of large uncertainties or unknown variations in plant parameters or structure [1]–[4]. In those papers, some adaptive laws are proposed to guarantee the stability of the system in the sense of Lyapunov. By com-bining other learning approaches, or by considering different control properties, various variations of adaptive fuzzy controlManuscript received October 29, 2003; revised February 14, 2004. This work was supported in part by the National Science Council of Taiwan under Grant NSC 89-2218-E-009-091. This paper was recommended by Associate Editor D. Y. Lee.
C.-C. Hsiao is with the Department of Electrical Engineering, National Taiwan University of Science and Technology, Taipei 106 Taiwan, R.O.C. He is also with the Department of Electrical Engineering, Fortune Institute of Technology, Kaoshiung, Taiwan 842, R.O.C.
S.-F. Su is with the Department of Electrical Engineering, National Taiwan University of Science and Technology, Taipei 106 Taiwan, R.O.C. He is also with the Department of Electrical Engineering, National Taipei University of Technology, Taipei, Taiwan 106, R.O.C.
T.-T. Lee is with the Department of Electrical and Control Engineering, Na-tional Chiao-Tung University. He is also with the Department of Electrical Engi-neering, National Taipei University of Technology, Taipei, Taiwan 106, R.O.C. C.-C. Chuang is with the Department of Electronic Engineering, Hwa-Hsia College of Technology and Commerce, Taiwan, R.O.C.
Digital Object Identifier 10.1109/TSMCB.2004.830338
approaches have been proposed in the literature [5]–[13]. In this paper, we reported our study on the issue of finding a suitable controller for a fuzzy system. In this study, the structure and pa-rameters of the fuzzy controller are fixed and we shall find a way of designing fuzzy controllers to satisfy requirements.
For the analysis of stability of fuzzy system, based on the Lya-punov stability criterion, Tanaka and Sugeno (T–S) [14] have proposed a useful theory for conservatively assuring the sta-bility of a Takagi-Sugeno-Kang (TSK) or T-S fuzzy model [15]. The theory states that if a common positive definite matrix re-quired in Riccati equations can be found for all fuzzy rules, the fuzzy model is stable in the sense of Lyapunov. Thathachar et al. [16] also proposed a necessary condition and a sufficient condi-tion for the stability of fuzzy systems. They showed that under a formal sufficient condition, a common Lyapunov matrix exists for all subsystems. It is easy to see that to analytically find such a matrix is a linear matrix inequality (LMI) problem [17], [41]. Based on the LMI concept, Kim et al. [18] proposed a numer-ical stability analysis method for singleton-type linguistic fuzzy control systems. Most of recent fuzzy control design approaches are to employ the parallel-distributed compensation (PDC) con-cept [19], in which controllers are designed individually for fuzzy rules and then stability condition is checked through LMI to validate the design. Some relaxed LMI stability conditions are also proposed in [20] and [21]. Parametric uncertainties re-garding those approaches are dealt with in [22]–[24]. However, those methods are stability checking approaches instead of de-sign approaches. When the dede-signed controller cannot satisfy the stability criterion, another controller is tried. Such a process is somehow a trial-and-error design procedure. Lam et al. [25] proposed a designing method that can be used to help solving the relaxed LMI problem and in the approach, the feedback gains of the subsystem are determined by using a genetic algorithm, which can also be viewed as a trial-and-error procedure. An-other problem rises when the number of rules is large because it may be difficult to find solutions for LMI in that case. More-over, since the validation of LMI is only for stability, the control performance assured in individual rules cannot be anticipated in the overall system performance under those design approaches. Several researchers [21], [26], [27] actually proposed ways of designing controllers by directly solving LMIs. Gao et al. [26] and Tanaka et al. [20] used LMIs combined with stable condi-tions of fuzzy systems to design a stable fuzzy system. When the control performance is considered, those approaches need to in-clude performance constraints into LMIs for all fuzzy rules [27]. Korba et al. [28] proposed an extended fuzzy scheduler (EFS) controller that can guarantee the stability and the tracking per-formance requirements. The idea is to introduce an additional 1083-4419/04$20.00 © 2004 IEEE
tracking-error state variable into the state variables of the con-trolled system, and then an extended-state feedback-gain matrix is design by means of LMIs. Cao et al. [29] also developed a two-part controller. One part is a state-feedback matrix like that in [17] and [20] and the other part is to satisfy global stable con-ditions. Note that in these approaches, the homogeneous fuzzy systems are considered. Here, “homogeneous” means that the consequent parts are linear equations without constant terms. Such fuzzy systems can only represent a certain class of non-linear systems. Kim et al. [30] proposed a discrete iterative LMI approach to analyze stability for discrete affine fuzzy systems, where “affine” means that the consequent parts are linear equa-tions with constant terms. However, the above approaches may become infeasible, when the number of rules is large. It is be-cause the analysis techniques are to find a common positive def-inite matrix for all subsystems (fuzzy rules) to fulfill the Lya-punov stability analysis. It is difficult to find such a matrix when the rule number is large. Sometimes, there does not even exist such a matrix.
Other approaches also exist that do not make use of the common Lyapunov matrix validation scheme. Kang et al. [31] proposed a controller that is inferred by using their consistency conditions [32], but the desired performance has not yet been addressed. Kiriakidis et al. [33] viewed a TSK fuzzy model as a linear system subject to a class of nonlinear uncertainties and claimed that the computational cost of checking such a stability criterion is less than that of finding a common Lyapunov matrix. However, this approach leads to a convex programming problem and the design procedure is still in a trial-and-error manner. Feng [34] proposed a sufficient condition, which leads to a search algorithm for solving a Riccati equation, and then a state feedback can be designed accordingly for such a system. Zak [35] also proposed a design algorithm to obtain a controller, which is separated into two parts to stabilize the nominal system and variations residing in all fuzzy rules, respectively. This approach is to treat variations of all rules as a whole in a robust control sense. For those approaches, when subsystems are distributed in a wide range, the upper bound of such variations may become large, and then the stabilization algorithm may fail. In addition, the control performance of the closed-loop system cannot be anticipated. In this paper, we proposed a novel robust control design approach that can design controllers directly for affine continuous or discrete time fuzzy systems and the closed-loop performance can be theoretically anticipated.
This paper is organized as follows. Section II describes the affine TSK fuzzy model. The proposed controller is introduced in Section III. Both continuous-time cases and discrete-time cases are discussed. Section IV shows simulation results for both continuous and discrete-time examples. Finally, Section V concludes the paper.
II. CONTROLDESIGN FORAFFINETSK FUZZYMODELS The considered problem is that a system is described by a set of fuzzy rules and we want to develop a way of designing
controllers for such a system. The considered fuzzy models are first introduced in [14] and the th rule of a discrete system is
Rule IF is and and is
THEN
(1)
where for , , and
are the input and past inputs, are fuzzy sets,
and , and are parameters in describing
the input and output relationships in the th fuzzy rule. Note that the premise part is only determined by ,
and and is independent to . This
relationship matches the properties of common systems. Be-sides, the consequence part contains a constant term, . Such a fuzzy model is referred to as a class of affine TSK fuzzy model [30]. The consequence part can be written in a state-space
form as , where
..
. ... ... . .. ...
and
Let be the membership degree of the in the
fuzzy set . Then the overall system can be inferred as (2) where is the rule number
with , and .
For a continuous TSK fuzzy model system, the th rule is of the form
Rule IF is and and is
THEN
(3)
where for with is the
time derivative of . Then, the consequence part can also
be written as , where
, and are the same as those in the dis-crete case, and . Similarly, the related items for a continuous affine TSK fuzzy model can be defined.
In the literature, based on the Lyapunov theorem, several de-sign approaches have been proposed to dede-sign stable controllers
for homogenous fuzzy models; i.e., the constant vector is ab-sent in (2). One of the most commonly used approaches is the parallel distributed compensation (PDC) control [19], [36], in which fuzzy controllers share the same premise parts with the considered fuzzy systems. The sufficient conditions for the sta-bility of the closed-loop system are summarized in [20]. It is required that the stability of the overall system be checked by solving LMIs [17]. If the common Lyapunov matrix cannot be found, another design is tried. It should be noted that the number of inequalities to be solved is . It can be found that when the rule number is large, it may be very difficult to solve those inequalities.
As mentioned earlier, there is another kind of approach [33], [35] in which a controller is defined for the nominal system of fuzzy rules first, and then the deviations from this nominal system existing in all rules are dealt with in a robust control fashion. Our approach shared the same idea as this kind of approach. The nominal system can be defined as
and , where
is a convex hull defined by the set of vertex matrices , and and a similar convex hull is defined for . Let
..
. ... . .. ...
and . The formation of and can be
ar-bitrary as long as they are stabilizable. Usually, a simple arith-metic average is taken; that is,
and . The differences between
and are
..
. ... . .. ...
(4)
where and . Then, the system (2) can
be rewritten as
(5)
where and . Similarly,
with the same definition as above, a continuous affine TSK fuzzy model can be written as
(6) Note that and are regarded as uncertainties in this kind of approaches.
III. HYBRIDCOMPENSATION CONTROLDESIGN FOR AFFINETSK FUZZYSYSTEMS
The design idea is to design a controller for each local model under the idea of PDC control [19], [36], in which fuzzy con-trollers share the same premise parts with the considered fuzzy systems. Then, the th control rule can be written as
Rule IF is and and is
THEN for
Thus, the overall fuzzy controller is . In
our study, a novel design approach, which consists of two parts of controllers to stabilize the nominal system and variations re-siding in all rules, respectively, is proposed. The propose feed-back control law can be written as
(7) where is to control the nominal system with the desired con-trol performance and is to compensate the variations in all rules individually. In the following, we shall introduce how the above control law is obtained. This type of control laws is called the hybrid compensation control (HCC) in our study. The control law proposed in [33] is referred to as the nominal com-pensation control (NCC) and the PDC controller [19], [36] is called the distributed compensation control (DCC). [35] also proposed a similar controller, in which the second part is to treat those variations as a whole instead of individually in a ro-bust control sense. If those subsystems are distributed in a wide range, the required norm bound conditions may not be satis-fied. In that case, the design algorithm will fail. This can be seen in our example shown later. For the proposed HCC, it is not required to find a common Lyapunov matrix for all sub-systems. This advantage greatly increases the applicability of our approach, especially when the rule number of the system is large.
As mentioned earlier, and [in (5) for the discrete case or in (6) for the continuous case] are regarded as uncertainties in our approach. For those terms, the following assumptions are made.
A1) The nominal part of the system (5) or (6) is stabilizable. A2) Uncertainties may vary with time within a prescribed
bounded set.
A3) There exists a 1 vector , a scalar such that
and .
Those assumptions are also used in [37] and [38] in dealing with uncertainties in the system matrix and input channels. In our case, since those uncertainties are in fact the summation of the deviations of all rules, it is easy to see that those assumptions can easily be satisfied. This can be verified in our control design for various systems. The control law designing methods for discrete and continuous TSK fuzzy models are derived in the following two subsections.
A. Discrete-Time Case
Consider a discrete TSK fuzzy model described by (5). Let
stabilize the nominal model in (5) and is to compensate the variations of all rules. Substituting (7) into (5), we have
(8)
where with
,
with , with
, and . In order to
let the system be stable, there must exist symmetry positive
definite matrices and such that .
Define and we have
where , . It is easy to verify
that when , the system is stable. Since
, if the compensation part is set as , then . Hence, we have
(9)
We then have the following theorem.
Theorem 1: Suppose that the chosen nominal system matrix
for the discrete fuzzy model system (1) is stabilizable. Then, the closed-loop system driven by the control law (7) is asymptotically stable in the large, where is the stable state-feedback gain for the nominal model and is given by (9).
Proof: With the compensation part of the control law in
(9), the equation holds. Thus, the closed-loop system (8) becomes
(10) Since is stabilizable, it proves the Theorem.
From Theorem 1, we can also conclude the following lemmas.
Lemma 1: The behavior of the discrete fuzzy model (1)
con-trolled by the control law (7) is the same as the closed-loop nom-inal model (10).
The closed-loop system is a linear system (nominal model) whose eigenvalues can be arbitrarily assigned by the state-feed-back gain . Hence, we can employ various stability design approaches, such as pole-placement, linear optimal control or other design techniques in designing controllers for the nom-inal model.
Lemma 2: Consider the fuzzy model system (1) without the
constant term. Suppose that the eigenvalues assigned for each subsystem are the same as that for the nominal model. Then the state feedback gain of the th subsystem is
(11) where , and , and are the state feedback gains of the th subsystem and of the nominal model, respectively.
It is easy to verify this lemma by simply substituting the feed-back gain into rules.
In (9), if s are the same sign in all rules that implies . In most of existing approaches, is always assumed. When
changes sign among rules for some , may
be near 0 or equal to 0. If such a situation occurs, it means that in a transition instant, the input can hardly change the system states. In other words, the system becomes uncontrollable. We think is only a transition state and usually, the system can still work well without this assumption. In our implementation, a threshold is used to avoid large input values for such situa-tions. As shown in Example 1, when changes signs among rules, the control input transits from large negative values to large positive values. By using a threshold, the input is limited to a reasonable range and the system still works well. We further analyze such a case in the following. If , it means that the inferred system is . It is an unforced system, and no matter what input is, the system behavior is uncontrol-lable. If the current uncontrollable state is an equilibrium state of , then there is no way of moving out this uncontrollable state. This is rarely the case and it is the problem of the system and is not caused by our control law. If not, the system will transit and then it is easy to find that because the system state is changed.
B. Continuous-Time Case
Similarly, we can derive the control law for continuous-time systems. The control law (7) is also used for a continuous TSK fuzzy model system (6). Since is Hurwitz stable, there exist symmetry positive definite matrices and such that
. Let , and we have
Obviously, if the inequality holds, the
system is asymptotically stable. We let ;
i.e., . Therefore
(12)
Clearly, (12) is the same as that for the discrete case; i.e., (9). In other words, Theorem 1 can also work for continuous fuzzy models. Consequently, Lemmas 1 and 2 also work for contin-uous fuzzy models.
Finally, the proposed HCC design method is summarized as follows.
Step 1) Select a stabilizable central rule as the nominal fuzzy model and calculate the variations for all subsystems by (3).
Step 2) Find a state feedback matrix such that the nom-inal fuzzy model in (8) is assigned the desired eigen-values. Such a can be designed by various tech-niques to provide specified system behaviors. Step 3) Get the compensation part by using (8) and
Fig. 1. Responses of using various controllers for the system in Example 1.
IV. DESIGNEXAMPLES
In this section, various examples are considered to illustrate good design performance of the proposed HCC design scheme.
Example 1: Consider an unstable continuous model, in
which there are two rules in the model and the system matrices are
Define the nominal system matrices as
and .
Let the desired eigenvalues are
and then . Define , we have
[33] for NCC. Such a design cannot guarantee the stability of the system. Using our HCC approach, the
com-pensation parts are ,
and , . Suppose that
the same eigenvalues are assigned for all subsystem (DCC).
From Lemma 2, we obtain and
. The solution for LMIs cannot be obtained for this case. In other words, the stability condition is not satisfied, and the controllers for all rules must be redesigned in the PDC approach. Fig. 1 shows the response of the three closed-loop systems for the initial condition . Simulations confirm the above assertions. Now, consider the approach in [35], since the norm bound of uncertainties is bigger than 1, that approach fails in this case. It should be noted that in this example changes signs among rules. We can find that the control input transits from large negative values to large positive values as shown in Fig. 2. By using a threshold, the input is limited to a reasonable range.
Fig. 2. Control input by using the proposed HCC for the system in Example 1.
Example 2: Consider a nonlinear discrete system in [39]
The TSK fuzzy model of such a system is derived in [31] and shown as follows:
IF is A is
THEN
where , , and
. Define the state vector and the
mem-bership functions are the same as those used in [31]. It can be found that the rule number is 7, LMI kinds of approaches may have difficulties in solving it. Now, the optimum control de-sign is used. The considered cost function is of the form
. Two situations are tested here
Design Case (I):
and
It is easy to verify that is stabilizable.
By minimizing , the required eigenvalues are
and then the state-feedback gain is
. The
com-pensation parts are
Design Case (II): By minimizing the cost
function , the desired eigenvalues become
. Thus, the state feedback gain is
and the compensation parts are , ,
, and , and
are the same as those in case (I).
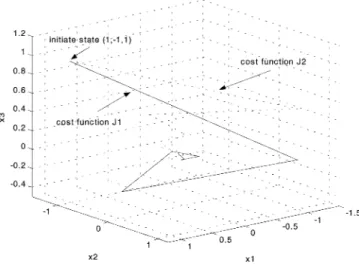
The simulation results are shown in Fig. 3 for the initiate state (1, , 1). It can be found that the overall system can indeed have good control performance as expected.
Example3: Consider the problem of balancing an inverted
pendulum on a cart. The dynamic equations are [40]
where and are the angle of the pendulum from the vertical and the angle velocity, is the mass of the pendulum, is the
mass of the cart, , is the gravity
constant, is the length of the pendulum, and is the force
Fig. 3. State trajectories of the nonlinear discrete system in Example 2. applied to the cart. Similar to [17], and . The fuzzy model can be approximated as [17]
where
and . The design specification is considered as no overshoot with the rising time 2 s.
We select the nominal fuzzy model as
and
It is easy to verify that is stabilizable. For the given specifications, the required two pole locations are .
Then, we have . From (8), the
com-pensation parts are
The controller is used for the initial conditions
. For the same desired pole locations, the PDC approach in [17] and the approach in [35] are also considered. The simulation results are shown in Fig. 4 and corresponding
Fig. 4. Angle responses of using various controllers for the system in Example 3.
TABLE I
RISE-TIMES OFZAK’S, PDCANDHCCFOREXAMPLE3
rise-time are listed in Table I. It can be found that our approach is the nearest one. Moreover, when the rise-time is 0.75 sec, the required two poles are about . By using our HCC approach, the simulation result and the rise-time are also shown in Fig. 4 and in Table I, respectively. It is clearly that HCC could achieve such a specification.
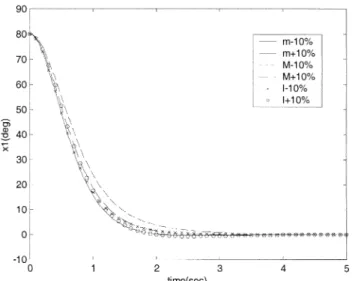
Since our approach is to directly compensate the uncertain-ties, robustness again parameter changes is an important issue. Nevertheless, our approach is derived in a Lyapunov control fashion. The obtained controller is always stable under a cer-tain range of uncercer-tainty. Thus, if a parameter slightly changes, we believe the proposed controller is robust. Fig. 5 shows the simulation results of changing (the mass of the pendulum), (the mass of the cart) and (the length of the pendulum), respectively, within , and without redesigning the con-trollers (two poles are located at ). It is evident that the responses of using our controller are only slightly changed even though the direct compensation is implemented. For the other two approaches, the changes are much less in our simulation. It is because those two approaches do not directly compensate those uncertainties and as a consequence, the effects of param-eter changes are small.
V. CONCLUSIONS
In this paper, we have proposed a method of designing controllers for affine TSK fuzzy models. In this approach, the controller is separated into two parts. The first one is to move the eigenvalues of the central rule to the desired locations. The second one is to individually compensate the variations residing in all rules. The design procedure is simple and effective. The stability analysis becomes the Lyapunov theorem for linear systems. Such an approach not only can result in the use of
var-Fig. 5. Angle responses of using the same HCC for the system with various parameter variations in Example 3.
ious control design techniques but also can guarantee desired performance of the closed- loop system. Various examples are conducted in the paper. Some of them even cannot be solved by other existing approaches. All results illustrated good control performances as desired.
REFERENCES
[1] M. Alata, C. Y. Su, and K. Demirli, “Adaptive control of a class nonlinear systems with a first-order parameterized Sugeno fuzzy approximator,”
IEEE Trans. Syst., Man, Cybern. C, vol. 31, pp. 410–419, Aug. 2001.
[2] C. Shi and A. D. Cheok, “Performance comparison of fused soft con-trol/hard observer type controller with hard concon-trol/hard observer type controller for switched reluctance motors,” IEEE Trans. Syst., Man,
Cy-bern. C, vol. 32, pp. 99–112, May 2002.
[3] Z. Huaguang and L. Cai, “Nonlinear adaptive control using the Fourier integral and its application to CSTR systems,” IEEE Trans. Syst., Man,
Cybern. B, vol. 32, pp. 367–372, Apr. 2002.
[4] Y. Tang and D. Vélez-Díaz, “Robust fuzzy control of mechanical sys-tems,” IEEE Trans. Fuzzy Syst., vol. 11, pp. 411–418, June 2003. [5] Y. G. Leu, T. T. Lee, and W. Y. Wang, “Online tuning of fuzzy-neural
net-work for adaptive control of nonlinear dynamical systems,” IEEE Trans.
Syst., Man, Cybern. B, vol. 27, pp. 1034–1043, Dec. 1997.
[6] , “Observer-based adaptive fuzzy-neural control for unknown non-linear dynamical systems,” IEEE Trans. Syst., Man, Cybern. B, vol. 29, pp. 583–591, Dec. 1999.
[7] W. Y. Wang, M. L. Chan, T. T. Lee, and C. H. Liu, “Adaptive fuzzy con-trol for strick-feedback canonical nonlinear systems withH tracking performance,” IEEE Trans. Syst., Man, Cybern. B, vol. 30, pp. 878–885, Dec. 2000.
[8] W. Y. Wang, M. L. Chan, C. C. J. Hsu, and T. T. Lee, “H tracking-based sliding mode control for uncertain nonlinear systems via an adap-tive fuzzy-neural approach,” IEEE Trans. Syst., Man, Cybern. B, vol. 32, pp. 483–492, Aug. 2002.
[9] S.-S. Chen, S.-F. Su, and T.-T. Lee, “Direct adaptive model reference fuzzy controllers,” in Proc. Chinese Automatic Control Conf., 2002, pp. 534–539.
[10] C. H. Wang, T. C. Lin, T. T. Lee, and H. L. Liu, “Adaptive hybrid intel-ligent control for uncertain nonlinear dynamical systems,” IEEE Trans.
Syst., Man, Cybern. B, vol. 32, pp. 583–597, Oct. 2002.
[11] S.-S. Chen, S.-F. Su, and Y.-C. Chang, “The stable tracking adaptive fuzzy control of nonlinear dynamic systems using the Takagi-Sugeno fuzzy logic,” in Proc. 7th Conf. Artificial Intelligence Applications, 2002, pp. 65–70.
[12] M. J. Er and Y. Gao, “Robust adaptive control of robot manipulators using generalized fuzzy neural networks,” IEEE Trans. Indt. Electron., vol. 50, pp. 620–628, June 2003.
[13] C. W. Tao, M. L. Chan, and T. T. Lee, “Adaptive fuzzy sliding mode con-troller for linear systems with mismatched time-varying uncertainties,”
[14] K. Tanaka and M. Sugeno, “Stability analysis and design of fuzzy control system,” Fuzzy Sets Syst., vol. 45, pp. 135–156, 1992.
[15] T. Takagi and M. Sugeno, “Fuzzy identification of systems and its appli-cation to modeling and control,” IEEE Trans. Syst., Man, Cybern., vol. SMC-15, pp. 116–132, 1985.
[16] M. A. L. Thathachar and P. Viswanath, “On the stability of fuzzy sys-tems,” IEEE Trans. Fuzzy Syst., vol. 5, pp. 145–151, Feb. 1997. [17] H. O. Wang, K. Tanaka, and M. F. Griffin, “An approach to fuzzy control
of nonlinear system: Stability and design issues,” IEEE Trans. Fuzzy
Syst., vol. 4, pp. 14–23, Feb. 1996.
[18] E. Kim, H. J. Kang, and M. Park, “Numerical stability analysis of fuzzy control systems via quadratic programming and linear matrix inequal-ities,” IEEE Trans. Syst., Man, Cybern. A, vol. 29, pp. 333–346, July 1999.
[19] K. Tanaka and M. Sano, “A robust stabilization problem of fuzzy control systems and its application to backing up control of a truck trailer,” IEEE
Trans. Fuzzy Syst., vol. 2, pp. 119–134, May 1994.
[20] K. Tanaka, T. Ikeda, and H. O. Wang, “Fuzzy regulators and fuzzy observers: Relaxed stability conditions and LMI-based designs,” IEEE
Trans. Fuzzy Syst., vol. 6, pp. 250–265, May 1998.
[21] M. Chadli, D. Maquin, and J. Ragot, “Relaxed stability conditions for Takagi-Sugeno fuzzy systems,” in IEEE Int. Conf. Syst., Man, Cybern., vol. 5, 2000, pp. 3514–3519.
[22] M. C. M. Teixeria and S. H. Zak, “Stabilizing controller design for un-certain nonlinear systems using fuzzy models,” IEEE Trans. Fuzzy Syst., vol. 7, pp. 133–142, Apr. 1999.
[23] K. Tanaka, T. Ikeda, and H. O. Wang, “Robust stabilization of a class of uncertain nonlinear systems via fuzzy control: Quadratic stabilizability, H control, and linear matrix inequalities,” IEEE Trans. Fuzzy Syst., vol. 4, pp. 1–13, Feb. 1996.
[24] H. K. Lam, F. H. F. Leung, and P. K. S. Tam, “Stability and robustness analysis and gain design for fuzzy control systems subject to parameter uncertainties,” in Proc. IEEE 9th Int. Conf. Fuzzy Syst., vol. 2, 2000, pp. 682–687.
[25] H. K. Lam, F. H. Leung, and P. K. S. Tam, “Design and stability anal-ysis of fuzzy model-based nonlinear controller for nonlinear systems using genetic algorithm,” IEEE Trans. Syst., Man, Cybern. B, vol. 33, pp. 250–257, Apr. 2003.
[26] W. Gao and J. Xie, “Design of stable fuzzy system based on LMI,” in
Proc. 3rd World Cong. Intelligent Control Automation, vol. 3, 2000, pp.
1552–1555.
[27] J. Joh, R. Langari, E. T. Jeung, and W. J. Chung, “A new design method for continuous Takagi-Sugeno fuzzy controller with pole placement con-straints: An LMI approach,” in Proc. IEEE Int. Conf. Systems, Man,
Cy-bernetics, vol. 3, 1997, pp. 2969–2974.
[28] P. Korba, R. Babuˇska, H. B. Verbruggen, and P. M. Frank, “Fuzzy gain scheduling: Controller and observer design based on Lyapunov method and convex optimization,” IEEE Trans. Fuzzy Syst., vol. 11, pp. 285–298, June 2003.
[29] S. G. Cao, N. W. Rees, and G. Feng, “Analysis and design of fuzzy control systems using dynamic fuzzy-state space models,” IEEE Trans.
Fuzzy Syst., vol. 7, pp. 192–200, Apr. 1999.
[30] E. Kim and D. Kim, “Stability analysis and synthesis for an affine fuzzy system via LMI and ILMI: Discrete case,” IEEE Trans. Syst., Man,
Cy-bern. B, vol. 31, pp. 132–140, Feb. 2001.
[31] G. Kang and W. Lee, “Design of TSK fuzzy controller based on TSK fuzzy model using pole placement,” in Proc. IEEE Int. Conf. Fuzzy
Sys-tems, vol. 1, 1998, pp. 246–251.
[32] G. Kang, “Fuzzy Modeling of Systems and Design of Fuzzy Controller,” Ph.D. dissertation, Dept. Syst. Sci., Tokyo Instit. Technol., Tokyo, Japan, 1987.
[33] K. Kiriakidis, A. Grivas, and A. Tzes, “Quadratic stability analysis of the Takagi-Sugeno fuzzy model,” Fuzzy Sets Syst., vol. 98, pp. 1–14, 1998. [34] G. Feng, “Approaches to quadratic stabilization of uncertain fuzzy dy-namic systems,” IEEE Trans. Circuits Syst. I, vol. 48, pp. 760–769, June 2001.
[35] S. H. Zak, “Stabilizing fuzzy system models using linear controller,”
IEEE Trans. Fuzzy Syst., vol. 7, pp. 236–240, 1999.
[36] H. O. Wang, K. Tanaka, and M. Griffin, “Parallel distributed compen-sation of nonlinear systems by Takagi and Sugeno’s fuzzy model,” in
Proc. IEEE FUZZ-IEEE, 1995, pp. 531–538.
[37] M. S. Mahmoud and A. A. Bahnasawi, “Asymptotic stability for a class of linear discrete systems with bounded uncertainties,” IEEE Trans.
Au-tomat. Contr., vol. 33, pp. 572–575, June 1988.
[38] W. Yang and M. Tomizua, “Discrete time robust control via state feed-back for single input systems,” IEEE Trans. Automat. Contr., vol. 35, pp. 590–598, Apr. 1990.
[39] K. S. Narendra and K. Parthasarathy, “Identification and control dynam-ical systems using neural networks,” IEEE Trans. Neural Networks, vol. 1, pp. 4–27, Mar. 1990.
[40] R. H. Cannon, Dynamics of Physical Systems. New York: McGraw-Hill, 1967.
[41] K. Tanaka and H. O. Wang, Fuzzy Control Systems Design and Analysis:
A LMI Approach. New York: Wiley, 2001.
Chih-Ching Hsiao received the B.S. and M.S.
degrees in electrical engineering from the National Taiwan Institute of Technology (NTIT), Taipei, Taiwan, R.O.C., in 1991 and 1993, respectively. He is currently pursuing the Ph.D. degree in electrical engineering from the same university.
He is an Instructor with the Department of Elec-trical Engineering, Fortune Institute of Technology, Kaohsiung Hsien, Taiwan, R.O.C. His research inter-ests include intelligent control and fuzzy systems
Shun-Feng Su (S’89–M’91) received the B.S.
de-gree in electrical engineering in 1983 from National Taiwan University, Taipei, Taiwan, R.O.C., and the M.S. and Ph.D. degrees in electrical engineering, in 1989 and 1991, respectively, from Purdue University, West Lafayette, IN.
He is a Professor of the Department of Electrical Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan, R.O.C. He is also a Professor with the Department of Electrical Engineering, National Taipei University of Tech-nology Taipei, Taiwan, R.O.C. and the Dean of the Affiliated College of Continuing Education at that University. His current research interests include neural networks, fuzzy modeling, machine learning, virtual reality simulation, intelligent transportation systems, data mining, and intelligent control.
Tsu-Tian Lee (M’87–SM’89–F’97) was born in
Taipei, Taiwan, R.O.C., in 1949. He received the B.S. degree in control engineering from the National Chiao Tung University (NCTU), Hsinchu, Taiwan, in 1970, and the M.S. and Ph.D. degrees in electrical engineering from the University of Oklahoma, Norman, in 1972 and 1975, respectively.
In 1975, he was appointed Associate Professor and in 1978 Professor and Chairman of the Department of Control Engineering at NCTU. In 1981, he became Professor and Director of the Institute of Control En-gineering, NCTU. In 1986, he was a Visiting Professor, and in 1987, a Full Professor of electrical engineering at University of Kentucky, Lexington. In 1990, he was a Professor and Chairman of the Department of Electrical En-gineering, National Taiwan University of Science and Technology (NTUST), Taipei, Taiwan, R.O.C. In 1998, he became the Professor and Dean of the Office of Research and Development, NTUST. In 2000, he was with the Department of Electrical and Control Engineering, NCTU, where he served as a Chair Pro-fessor. Since 2004, he has been with National Taipei University of Technology (NTUT), where he is now President. He has published more than 180 refereed journal and conference papers in the areas of automatic control, robotics, fuzzy systems, and neural networks. His current research involves motion planning, fuzzy and neural control, optimal control theory and application, and walking machines.
Dr. Lee received the Distinguished Research Award from National Science Council, R.O.C., from 1991 to 1998, the TECO Sciences and Technology Award from the TECO Foundation in 2003, the Academic Achievement Award in En-gineering and Applied Science from the Ministry of Education, R.O.C., in 1998, and the National Endow Chair from the Ministry of Education, R.O.C., in 2003. He was elected to the grade IEE Fellow in 2000. He became a Fellow of New York Academy of Sciences (NYAS) in 2002. His professional activities include serving on the Advisory Board of Division of Engineering and Applied Science, National Science Council, serving as the Program Director, Automatic Control Research Program, National Science Council, and serving as an Advisor of Min-istry of Education, Taiwan, and numerous consulting positions. He has served as Member of Technical Program Committee and Member of Advisory Committee for many IEEE sponsored international conferences. He is now the Vice Presi-dent for Membership, a member of the Board of Governors and the Newsletter Editor of the IEEE Systems, Man, and Cybernetics Society.
Chen-Chia Chuang received the B.S. and M.S.
degrees in electrical engineering from National Taiwan Institute of Technology, Taipei, Taiwan, R.O.C., and the Ph.D. degree in the electrical engineering at the National Taiwan University of Science and Technology, Taipei, in 1991, 1993, and 2000, respectively.
He is currently an Assistant Professor with the De-partment of Electronic Engineering, Hwa-Hsia Col-lege of Technology and Commerce, Taipei, Taiwan, R.O.C. His current research interests are neural net-works, data mining, neural fuzzy systems, and signal processing.