A Unifying Approach to Determine the Necessary
and Sufficient Conditions for Nonblocking
Multicast 3-Stage Clos Networks
F. K. Hwang
Abstract—The 3-stage Clos network is the most-studied
switching network. However, exact conditions on the strictly nonblocking multicast three-stage Clos network under various models are difficult to get, due to the messy detail and because each case employs a different argument. Hwang and Liaw made the latest attempt and pointed out errors in previous attempts. However, they made errors, too. In this paper, we propose a unifying approach to study those models systematically (which also applies to some wide-sense nonblocking (WSNB) networks). We also propose a new routing algorithm, and use the unifying approach to derive a necessary and sufficient condition for WSNB.
Index Terms—3-stage Clos network, strictly nonblocking
switching network, wide-sense nonblocking (WSNB) switching network, window algorithm.
I. INTRODUCTION
A
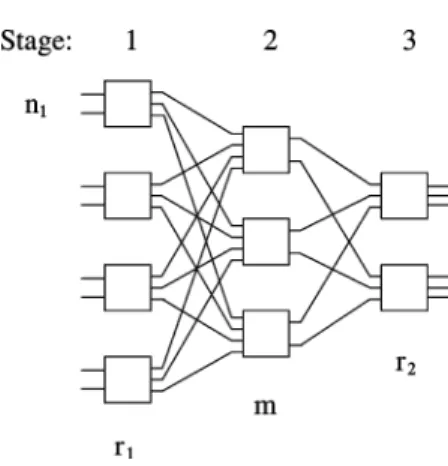
3-stage Clos network [1] hasswitches of size in the input stage (stage 1), switches of size in the middle stage (stage 2), and switches of size in the output stage (stage 3). Every middle switch has exactly one link to each input switch and
each output switch. Thus, the network has inputs
and outputs (see Fig. 1).
Each switch is assumed to be nonblocking, in the sense that any one-to-one mapping between its inputs and outputs can be connected simultaneously. A switch is said to have fan-out capa-bility if any one-to-many mapping between its inputs and out-puts can be connected. Under multicast traffic, each input can request to connect to many idle outputs. A request is called an -request if the number of outputs involved is . In an -cast traffic, no -request is allowed for . A network is -cast strictly nonblocking (SNB) if it can always route an -request, , regardless of how existing connections are routed. It is -cast wide-sense nonblocking (WSNB) if routing is possible under the condition that all requests are routed according to a given routing strategy.
Giacomazzi and Tricordi [3] first studied necessary and
suffi-cient conditions for to be SNB for -cast
traffic. (Although Masson and Jordan [8] wrote a paper some 20
Paper approved by D. K. Hunter, the Editor for Optical Communication of the IEEE Communications Society. Manuscript received February 24, 2003; re-vised April 14, 2004. This work was supported in part by the Republic of China National Science Council under Grant NSC-91-2115-M-009-010, and in part by the LI-MCI Center.
The author is with the Department of Applied Mathematics, National Chiao Tung University, Hsinchu 20050, Taiwan, R.O.C.
Digital Object Identifier 10.1109/TCOMM.2005.852839
Fig. 1. C(2; 4; 3; 2; 3) with eight inputs and six outputs.
years earlier, giving a sufficient condition for SNB in a multicast 3-stage Clos network, this network was later [2] determined to be WSNB). Let denote the number of middle switches re-quired for SNB. Giacomazzi and Tricordi gave the following necessary and sufficient condition:
(1) where indicates that the current request is -cast, is the number of outputs connected by other inputs on the same input switch as , and
is the maximum number of connections over all requests going to at least one of the output switches involved in the current request.
Note that (1) is complicated and implicit, since one has to maximize over three variables. No closed-form solution was given in [3]. Recently, Pattavina and Tesei [9] gave a counterex-ample against (1).
Giacomazzi and Tricordi also gave a similar equation for the model where the input stage has no fan-out capability.
Hwang and Liaw [6] used a different approach to obtain a necessary and sufficient condition for SNB in a -cast 3-stage Clos network
(2) where the second term reflects the boundary condition from the input size, and the third term reflects the boundary condition from the output side. Compared with (1), (2) is explicit and
easily computed. Pattavina and Tesei extended (2) to the case that a multicast call must connect to at least outputs.
Call this model, which assumes fan-out capability for every switch, model 0. Hwang and Liaw also gave similar equations to models 1, 2, and 3, where model assumes that switches in stage have no fan-out capability. Note that such a model can also be treated as a WSNB [4], [5] network by interpreting that no fan-out in stage is not due to the lack of capability of the switch, but due to the rule of a routing strategy.
Hwang and Liaw also studied a genuine WSNB model, in which an -request can have at most one path going to an output switch, regardless of how many outputs on that switch are in-volved in the request. This routing strategy is called “no-split,” and was the one used in [8].
Actually, Hwang and Liaw considered two cases for each of the above five models according to whether a busy input can generate another request by adding extra outputs to existing ones. If this is not allowed, the traffic is closed end; otherwise, it is open end. So, in total, they gave ten sets of necessary and sufficient conditions.
In this paper, we revise these ten sets of necessary and suffi-cient conditions. Our method is similar to Hwang and Liaw, but some intricate points are more carefully analyzed. In particular, we develop a unifying approach which works for all ten cases, instead of the case-by-case arguments given in [6]. This system-atic approach discovers some errors in [6], and allows an easy check on the correctness of the current results. We also propose a new WSNB algorithm using the window algorithm (to be de-fined in Section IV) first proposed by Tscha and Lee [10], and also studied by Kabacinski and Danilewitz [7] for the
multi-network. We use the unifying approach to derive necessary
and sufficient conditions for to be WSNB
under the window algorithm. Interestingly, models 1 and 2 be-comes two special cases where the window size is maximum or minimum.
II. A UNIFYINGAPPROACH
Our approach gives a more systematic and orderly counting to the number of blocked middle switches. Let the current request be from input on switch to outputs on a set of switches. Then the order is blocking by paths from , blocking by paths from other input switches, blocking by paths from . Such an ordered counting allows us to eliminate duplicated counting. We also highlight the notion of the minimum number of middle switches required to connect the current requests when blocking from other paths is ignored. This notion helps to crystalize the counting. While previous approaches are not devoid of the above elements, they are usually less explicit and exact.
Let denote the potential maximum number of middle switches occupied by paths from which cannot use, while ignoring the boundary effect from the output side, i.e., there are only outputs. Then the actual maximum number, after considering the boundary effect, is
(3)
since each path through these middle switches must end at a distinct output, but there are only of them available.
Suppose involves outputs on several output switches. In general, it suffices to consider just one of them, since they do not compete for links to the middle stage, and the condition derived for one is the same for another. An exception is when those output switches involved in are required to be routed through the same middle switch, as in model 1, then we must consider the output switches together, because a failure to reach one output switch is a failure for all.
First consider the case where connections to the switches in are independent. Let be an output switch containing outputs in . Then each of the other outputs can occupy a distinct middle switch, as long as there are enough inputs to generate requests involving these outputs. Since paths generated by inputs of are already counted in (3), there are inputs available. Let denote the potential max-imum number of middle switches the paths from these
inputs can occupy while ignoring the output side.
Another point to consider is that some of the outlets
may already be used in (3). There are outlets
not in the -request and not from . So if
then
among the outputs from are already consumed in (3).
Hence, only outputs from can generate new
paths, where . Summarizing, the maximum
number of new paths generated by available outputs from is (4) Let denote the minimum number of middle switches required to guarantee the routing of when there is no other connection. Then to route among other connections, we must have additional switches not counted in (3) and (4). In the worst-case scenario, where the switches in (3) and (4) are all distinct, then a sufficient condition to route is
(5) obtained by pairing with each term in the second min. Note that if the first min is , then the second min must be
, and the condition becomes ,
which is same as the last term in (5). A careful examination of the above arguments reveals that the worst-case scenario gen-erating (3) and (4) can happen, hence, (5) is also a necessary
condition. For , then , ,
and , (5) is then reduced to ,
To save writing, let denote the number such that
is necessary and sufficient for to be -cast
SNB (WSNB for the no-split model).
Lemma 1: Suppose the routings of to the output switches in are independent. Then
Corollary 2: If is independent of , then
Lemma 1 applies to models 0, 2, 3, and no-split, while Corol-lary 2 applies to any model whose output stage has fan-out ca-pability.
A traffic model is called consistent if every pair of paths from the same input, if legitimate separately, is a legitimate pair under the model. None of models 1, 2, or 3 is consistent, since two le-gitimate paths can go through the same stage- switch and force a fan-out at that switch. Nor is the no-split model consistent, since the two paths going to the same output may go through different middle switches.
Lemma 3: for open-end traffic is same as the closed-end case for a consistent model.
Proof: It was proved in [6] that if is sufficient for open-end traffic, then it suffices for closed-end traffic. There-fore, we only need to prove the converse.
Consider an -cast request from input in open-end traffic
such that is already connected to outputs, .
We modify the traffic by deleting the requests (and connections) from to these outputs, and add them to the -cast request. Further, any set of existing requests from an input are interpreted as one request with the set of connecting paths intact. Then the modified traffic is closed end, hence, the current
-cast request from is routable.
Back to the original open-end traffic. We route the -cast re-quest using the same paths as in the modified traffic. Note that all existing paths, other than those from , are same as in the modified traffic. So any overlapping of these paths with existing ones must be with paths from . Since the model is consistent, all paths from the same input can co-exist.
Although the notion of consistency has limited applicability in Lemma 3, we will see in the next section that with modifica-tions, it can apply to various models.
III. NECESSARY AND SUFFICIENT CONDITIONS FORTENMODELS
We apply the results obtained in Section II to the ten models studied in [6].
Theorem 4: For model 0 under closed-end traffic
Proof: , , and
. By Corollary 2
at Corollary 5: Open-end traffic has the same .
Proof: Follows from Lemma 3.
Theorem 6: For model 2 under closed-end traffic
Proof: , , and
, since if , additional middle
switches still suffice by routing each such middle switch to a distinct output switch, and then using the fan-out capability of the output switches to reach multiple outputs. The reason that
, but not , is in and is because under
the SNB rule, each connection can be routed arbitrarily, as long as the paths are available. Hence, a connection can use two dif-ferent paths to reach two inputs on the same output switch, even if it is a waste. By Corollary 2
at
Theorem 7: For model 2 under open-end traffic
Proof: Unlike the case in Corollary 5, the middle switches cannot fan out. Hence, cannot use a middle switch already carrying a path from to route . Since can connect
to a maximum of outputs, while can already have
connected to a maximum of outputs, .
, and are same as the open-end case. By Corollary 2
at any
Note that the conditions for closed-end traffic and open-end traffic are different, contrary to the conclusion in [4]. We give an example that in Theorem 6 is not sufficient for open-end traffic.
Example: Consider with . Then
has inlets , has inlets , and has
outlets for
. Then in Theorem 6 and in
Theorem 7. Let be the ten middle switches.
The current request is , and the existing paths
, , , ,
, and . Then none of the can
carry .
Theorem 8: For model 3 under closed-end traffic
Proof: It is easily argued that and
. To derive , note that if involves out-puts on the same output switch, then these outout-puts must each be routed through a distinct middle switch. On the other hand, out-puts of different output switches can be routed through the same middle switch. Let denote the maximum number of outputs on
the same output switch. Then , where .
By Lemma 1
at at
since if , then
Theorem 9: Open-end traffic has the same .
Proof: We use the same method as in the proof of Lemma 3, but with some modification. Note that with the modified traffic, the paths from to outputs in the same output switch must go through different middle switches. Further, these paths can be interchanged without affecting the routability. We will make necessary interchanges, such that no path from to
goes through a middle switch which routes to
in an existing path in open-end traffic. Then we can route the current request under open-end traffic by using the paths in the modified traffic.
Theorem 10: For the no-split algorithm under closed-end traffic
Proof: An -request can use at most paths to
reach the output stage. Hence, and
, while (since there is
no other connection, any middle switch will do). By Corollary 2
at
Theorem 11: Open-end traffic has the same .
Proof: If the current request from contains an output from the same output switch , such that there exists a path from to , then use the same path to route . So we may assume that the current request contains only outputs whose output switches are not connected to . Use the same method as given in the proof of Lemma 3 to route them, since the path from to these outputs can coexist with existing paths from .
Finally, we deal with model 1. In this model, we need to find one middle switch which can route to all output switches in .
Therefore, we must replace in (4) by . The
corresponding change in from Lemma 1 is
(6) Theorem 12: For model 1 under closed-end traffic
where
Proof: Since each -request must go to a single middle
switch, , , and .
Further, outputs in which are on the same must be con-nected through the same path, and then reached through the
output switch fan-out. Thus we may assume . By
(6)
at the maximum value of
Since the first term is increasing in , and the third decreasing, the maximum should occur at
which is solved by if the integrability of is ignored. It is easily verified that the maximum occurs either at or . Further
For open-end traffic, it was shown in [4] that no is large enough to guarantee SNB.
IV. WIDE-SENSE NONBLOCKING UNDER THEWINDOWALGORITHM
We first describe the window algorithm. Partition the output switches into sets of (assuming divides ), and call each set a window. An -request involving outputs in windows will
be treated as multicast requests, where the th subrequest in-volves only the outputs in window . Each subrequest must be routed through one middle switch only, while two subrequests from the same input are treated as different requests, and hence, cannot be routed through the same middle switch.
Let denote the sum of . Note that the window algorithm implies the no-split rule, since two outputs on the same output switch must be in the same window, and their routes go through the same middle switch. Clearly, their routes must also go through the same link between that middle switch and their output switch. Therefore, in deriving the tightest nonblocking condition, we may assume that each -request involves at most one output from an output switch. Hence, is also the number of output switches in window involved in the -request.
Clearly, , , and
.
Theorem 13: For the -window algorithm under closed-end traffic
where
Further, if , then
Proof: Suppose the request consists of subrequests. Note that each subrequest involves a distinct set of outputs. We compute the maximum number of middle switches needed to connect subrequest . Since each subrequest is connected through a single middle switch, the connections of the other subrequests consume middle switches, regard-less of the numbers of outputs in these subrequests, as long as they are positive. Therefore, the worst case for subrequest
occurs when is maximum, with and fixed, i.e., . Since the subrequests are interchangeable, the worst-case number of middle switches that suffices for one subrequest suffices for all.
Since each subrequest is routed through a single middle switch, (6) for model 1 can be used to compute the number of middle switches required to connect subrequest , except
replacing . To compute for connecting
, we also have to maximize over and , and add the middle switches required to connect the other subrequests. Since consists of at most
subrequests, we have ,
Fig. 2. Request(u ; y ) is unroutable.
, , and
(7) by changing the variable from to . Setting equal the two terms in (7) containing , we obtain the first term of . The second and third terms represent some boundary conditions imposed by the other two terms in (7).
Clearly, the maximum is obtained at either or ,
and at . At , we can
drop the third term of (6), as it is larger than the first term. At , we can drop the first term.
Thus, Theorem 13 follows.
Corollary 14: For , in Theorem 13 is the same as in Theorem 12.
Proof: For , and
, where was given in Theorem 12. Corollary 14 is easily verified.
Corollary 14 is not surprising, since if all output switches are in the same window, then every -cast request must be routed through the same middle switch, the same constraint as in model 1.
Corollary 15: For , .
Proof: For , . Corollary 15 easily follows
from Theorem 13 with .
The in Corollary 15 is same as in model 2, except is replaced by . This difference is due to the fact that no-split is forced under the window algorithm, but not in model 2.
Fig. 2 shows that for open-end traffic under the window
algo-rithm, cannot guarantee WSNB, no matter
TABLE I
RESULTS OF THEFIVEMODELS(FIRSTROWREPRESENTSCLOSED-END, SECONDROW, OPEN-END,AND3 INDICATESEITHER ANEWRESULT OR ACORRECTPROOF ISNOWPROVIDED)
request is unroutable, since it must be routed through under the window algorithm, but the link from to is occupied. Contrasting this example with Theorem 13, we see a qualitative difference between the closed-end and the open-end traffic for the window algorithm (just as for model 1).
The window algorithm offers a continuum of choices between models 1 and 2. It also compares favorably with models in Sec-tion II. As we said, model 1 corresponds to choosing , and model 2 is close to, but dominated by, the choice . For large (for example, the unconstrained broadcast case, where ), models 0, 2, 3, and the no-split algorithm essentially require middle switches, while the window algorithm
re-quires by choosing . On the other hand, for
small, we can choose , such that the window algo-rithm essentially requires the same number of middle switches as models 0, 2, 3, and the no-split algorithm.
V. CONCLUSIONS
We summarize our results in Table I for easy comparisons. There are several interesting findings.
1) The network in model 0 is more powerful (and more costly) than the networks in models 1, 2, 3. Yet in model 0 is only slightly better than those in models 2 and 3, and not comparable to in model 1. This sur-prising phenomena, that a more powerful network may not have better performance, is due to the fact that in the SNB setup, if you give the routing freedom to do stupid things, it will.
2) of the no-split is same as model 0 except for replacing
by , an improvement if . The
improvement is not surprising, since the no-split model guarantees WSNB, while model 0 guarantees SNB. 3) The boundary effect from the output side is uniformly
, except in model 1. This is because only in model 1, the three terms in contain one term increasing in , and another (the output boundary) decreasing in , resulting in an -value which is not an extreme value.
The window algorithm not only provides a continuum of choices, but also some interesting connections between the models in Section II. For example, models 1 and 2 correspond to the two extreme cases of the window algorithm. Also, we have known that model 1 implies the no-split rule, and model 3 contradicts the no-split rule; now we further know the con-sequence of combining model 2 and the no-split rule. We have also shown that the performance of the window algorithm is about the same as others for small, but can be much better for large.
ACKNOWLEDGMENT
The author wishes to thank the reviewers for many helpful comments, the Associate Editor for an efficient handling of the review process, and Ms. B.C. Lin for a careful proofreading.
REFERENCES
[1] C. Clos, “A study of nonblocking switching network,” Bell Syst. Tech.
J., vol. 32, pp. 406–424, 1953.
[2] P. Feldman, J. Friedman, and N. Pippenger, “Wide sense nonblocking networks,” SIAM J. Discr. Math., vol. 1, pp. 158–173, 1988.
[3] P. Giacomazzi and V. Tricordi, “A study of nonblocking multicast switching networks,” IEEE Trans. Commun., vol. 43, no. 2–4, pp. 1163–1165, Feb.-Apr. 1995.
[4] F. K. Hwang, “Three-stage multiconnection networks which are non-blocking in the wide sense,” Bell Syst. Tech. J., vol. 58, pp. 2183–2187, 1979.
[5] F. K. Hwang and A. Jajszczyk, “On nonblocking multiconnection net-works,” IEEE Trans. Commun., vol. COM-34, no. 10, pp. 1038–1041, Oct. 1986.
[6] F. K. Hwang and S. C. Liaw, “On nonblocking multicast 3-stage Clos network,” IEEE Trans. Netw., vol. 8, no. 4, pp. 535–539, Aug. 2000. [7] W. Kabacinski and G. Danilewicz, “Wide-sense and strict-sense
non-blocking operation of multicast multi-log N switching networks,”
IEEE Trans. Commun., vol. 6, no. 6, pp. 1025–1036, Jun. 2002.
[8] G. M. Masson and B. W. Jordan, Jr., “Generalized multi-stage multicast connections network,” Networks, vol. 2, pp. 191–209, 1972.
[9] A. Pattavina and G. Tesei, “Multicast nonblocking switching networks,”
IEEE Trans. Commun., vol. 50, no. 8, pp. 1240–1243, Aug. 2002.
[10] Y. Tscha and K. H. Lee, “Yet another result on multi-log N networks,”
IEEE Trans. Commun., vol. 47, no. 9, pp. 1425–1431, Sep. 1999.