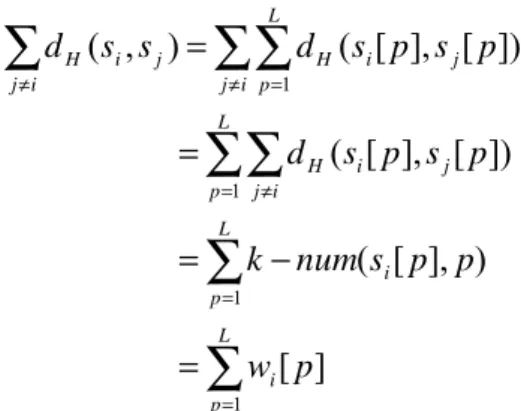Efficient Algorithms for Some Variants of the Farthest String Problem

Efficient Algorithms for Some Variants of the

Farthest String Problem

Chih Huai Cheng, Ching Chian Huang, Shu Yu Hu, Kun-Mao Chao

Department of Computer Science and Information Engineering

National Taiwan University

Taipei, Taiwan 106

{b89010, b89037, b89117, kmchao}@csie.ntu.edu.tw

Abstract

The farthest string problem (FARTHEST STRING) is one of the core problems in the field of consensus word analysis and several biological problems such as discovering potential drugs, universal primers, or unbiased consensus sequences. Given k strings of the same length L and a nonnegative integer d, FARTHEST STRING is to find a string s such that none of the given strings has a Hamming distance that is smaller than d from s. It has been shown to be NP-complete. In this paper, we study two variants of FARTHEST STRING. One is to search for a string s satisfying the condition that the hamming distances between s and all the given strings are greater than d. We give an O((|Σ|(L-d))(L-d) _{)-time algorithm, where |}

Σ| is the alphabet size. The other variant is to find a string s such that the sum of the hamming distances between s and all the given strings are maximized. We solve this problem in O( kL ) time.

1 Introduction

With the development of genetic technology, more and more problems are solved by using genetic information. We can distinguish related species from other species by comparing the DNA difference

between one another [7]. All these problems can be reduced to finding a pattern which occurs in one set of strings (the Closest String problem) but does not occur in another set (the Farthest String problem) [6]. FARTHEST STRING is an important problem in computational biology. This paper proposes efficient algorithms to solve the following two problems. The first one is the farthest string problem with fixed parameters. Where k strings with length L and a non-negative number d is given, the problem is to determine whether a string s that satisfies the condition that the hamming distance between s and all the given strings are greater than d. The second problem is to find the farthest string s under the condition that s must reside in the set of the given strings and has the maximum sum of hamming distance with respect to all other strings.

The farthest string problem is proven to be NP-complete [8] and there is a polynomial-time approximation scheme (PTAS) for the farthest string problems based on a linear programming relaxation technique [8]. Now, consider the two most natural parameters concerning farthest strings: the minimum Hamming distance d and the number of given input strings k. In some applications d is (very) large, so it is important to ask whether efficient algorithms are possible when d or k is fixed. FARTHEST STRING,

although NP-complete in general, is tractable [2, 5] for fixed parameters d andΣby using the bounded search tree algorithm [1, 3, 4].

The rest of the paper is organized as follows. In Section 2, we give the general strategy and the main idea of the algorithm for the farthest string problem with fixed parameters and show the running time and correctness under the condition of binary strings first. Next, we extend the result to arbitrary alphabet instances. In Section 3, we give a formal definition of the variant of the farthest string problem and propose an efficient algorithm to solve the problem in O(kL). We then prove the correctness and time complexity of the algorithm.

2 Farthest string with fixed parameter

As we stated in the introduction, the farthest string problem here is given k strings with the same length L and a non-negative number d, and trying to find a string s that satisfies the condition that the hamming distance between s and all the given strings are greater than d. We give the formal definition of the farthest string problem in mathematical terms:

Input: Strings s1, s2, . . . , sk over alphabetΣof length L ,

and a nonnegative integer d.

Question: Is there a string s of length L such that dH(s,

si) >= d for all i = 1, . . . , k?

Before presenting the algorithm for this problem, we give some definitions and minor results that will be used in the algorithm.

Lemma 1. Given a set of strings S = { s1, s2, . . . , sk }

and a positive integer d. If there are i, j ∈{1, . . . , k} with dH(si, sj) > x, then there is no string s with

mini=1,...,k {dH(s, si )} > L-x/2.

Proof. Suppose the hamming distance between si and sj

is greater than x, this means that there are at most L-x positions with the same symbol and at least x positions with different symbols at the same relative positions on si and sj. To achieve the greatest hamming distance

between si and sj simultaneously, the complement of

the symbol on all of the positions where si and sj

contain the same symbol is chosen. Thus we increase the hamming distance for si and sj by at most L-x, on

the other hand, changing a symbol on the other positions where si and sj have different alphabets can

increase the hamming distance by only at most x/2. Therefore the maximum hamming distance that an arbitrary string may have between si and sj is L-x + x/2

= L-x/2 when dH(si, sj) = x. Hence, when dH(si, sj)> x

the maximum hamming distance on both si, sj cannot

exceed L-x/2.

Corollary 1. Given a set of strings S = { s1, s2, . . . ,

sk } and a positive integer d. If there are i, j ∈{1, . . . ,

k} with dH(si ,sj)> 2L-2d, then there is no string s with

mini=1,...,k {dH(s, si )} >= d.

Proof. By lemma1, we set L-x/2 = d and then the value of x can be deduced easily. We can find that x = 2d-1L, and therefore no string s exist that satisfies the condition that mini=1,...,k dH(s, si ) >= d.

Given a string s then

s

is the string defined by

taking the complement alphabet of every position on string s. If s is a binary string then the job is to simply exchange the 1’s to 0’s and the 0’s to 1’s. If the alphabet set of s contains more than two elements, then for each string the complement string may have more than one choice. E.g. when the alphabet set = {0,1,2} then the complement of alphabet 0 may be 1 or 2.

Lemma 2. Given a set of strings S = { s1, s2, . . . , sk }

and a positive integer d. If there are i, j ∈{1, . . . , k} with dH(

s

i, sj)< 2d-L, then there is no string s with

mini=1,...,k{dH(s, si )} >= d.

Proof. The hamming distance between complement of si and sj is smaller than 2d-L, it means that there

are at most 2d-L positions with different symbols at the same relative positions on

s

i and sj. In other

words, there are at least L-(2d-L) = 2L-2d positions with different symbols at the same relative positions on si and sj. By the corollary mentioned above,

lemma2 is proved.

The idea of our algorithm is to start with one of the given strings, e.g.,

s

₁, as a “candidate string.” If

there is a string si, i = 2, . . . , k, that differs from the

candidate string in less than d positions, we recursively try several ways to move the candidate string “away from” si; the term “moving away” means that we select

a position in which the candidate string and si have the

same alphabet and set this position in the candidate string to the complement of the character of si at this

position. We stop either if we moved the candidate “too far away” from

s

₁ or if we found a solution. By a

careful selection of subcases of this recursion we can limit the size of this search tree to O(((|Σ|(L-d))(L-d) _),

as will be shown in the following theorem. In Figure 1 we outline a recursive procedure solving FARTHEST STRING. It is based on the bounded search tree paradigm that is frequently successfully applied in the development of fixed-parameter algorithms [1, 4, 6].

Recursive procedure FSD(s,Δd)

Global variables: Set of strings S = { s1, s2, . . . , sk},

integer d.

Input: Candidate string s and integerΔd.

Output: A string

sˆ

with mini=1,...,k {dH(

sˆ

, si )} >= d if it

exists,

and “not found,” otherwise.

(D0) If Δd < 0, then return “not found”;

(D1) If dH(s, si) < 2d - L for some i ∈{1, . . . , k}, then

return “not found”;

(D2) If dH(s, si ) >= d for all i = 1, . . . , k, then return s;

(D3) Choose any i ∈{1, . . . , k} such that dH(s, si) <

d:

P := {p | s[p] = si [p]};

Choose any P’

⊂

P with |P’| = L - d + 1; For every p∈P’ do

s’ := s; s’[p] :=

s

_i

[ p

]

;

sret := FSd(s’,Δd − 1);

If sret

≠

“not found”, then return sret;

(D4) Return “not found”

Fig.1 The algorithm we propose to search the farthest string. The recursive procedure creates a bounded search tree that traverses to discover the farthest string. Theorem 1 Given a set of binary strings S = { s1, s2, . . . , sk }of length L, and an integer d,

Algorithm FSD (Figure 1) determines in

O( kL(L-d)(L-d) _{) time whether there is a string with}

mini=1,...,k {dH(s, si)}>= d and it computes such an s if

one exists. Proof.

Running time. We consider the recursive part of the algorithm. ParameterΔd is initialized to L-d. Every recursive call decreasesΔd by one. The algorithm stops whenΔd < 0. Therefore, the algorithm builds a

search tree of height at most d. In one step of the recursion, the algorithm chooses, given the current candidate string s, a string si such that dH(s, si) < d. It

creates a subcase for L-d + 1 of the positions in which s and si have the same alphabet. This yields an upper

bound of (L-d + 1)L-d _{= O((L-d)}L-d _{) on the search tree}

size.

Correctness. Let us consider the situation when we first

enter the recursive procedure. In the first recursive call the candidate string s is

s

₁. If

s

₁satisfies the condition

that the hamming distance between

s

₁and si is no lesser

than d, then we have our answer; If

s

₁does not satisfy

the above condition and a furthest string s does indeed exist, then there exists some string si such that dH(

s

₁, si)

< d. So

s

₁and si have at most d-1 positions that have

different alphabets (one symbol is 0 and the other one is 1); in other words there are at least L-d+1 positions that contain the same alphabet. Since by assumption s is the farthest string, therefore s must satisfy the below conditions: s and si have at least d positions that

contain different alphabets; in other words there at most L-d positions containing same alphabets. So by the pigeonhole theorem, if we select L-d+1 positions from

s

₁, and substitute it with the complement (choose

0 when alphabet is 1 ; choose 1 when alphabet is 0), then one of the changes must certainly make

s

₁closer

to the farthest string s. In the each following recursive procedure will make the candidate string s (the parameter of FSD) closer to the farthest string (if the farthest string exists). So after the execution of the algorithm we will find the farthest string s if it exists.

Theorem 2 Given a set of |Σ| alphabet strings

S = { s1, s2, . . . , sk }of length L, and an integer d,

Algorithm FSD (Figure 1) determines in O( kL((|Σ |(L-d))(L-d) _{) time whether there is a string with}

maxi=1,...,k dH(s, si)>= d and it computes such an s if

one exists.

Proof. We extend the result to arbitrary symbols. The basic pseudo-code of the algorithm does not change, but in the case of choosing the complement of the alphabet, the branch factor of the bounded search tree is increased. In the case of binary alphabets, the pth position of si’s complement is either a change from 0 to

1 or 1 to 0. When we extend the case to non-binary alphabets, the complement may have more than one choice possible, for example, when the alphabet set = {0,1,2} then the complement of 0 may be 1 or 2. Similarly in the beginning of the procedure call, if

s

₁satisfies the condition that the hamming distance

between

s

₁and si is no lesser than d, then we have our

answer; if

s

₁does not satisfy the above condition and a

farthest string s does indeed exist, then there exists some string si such that dH(

s

₁, si) < d. Like the proof

above,

s

₁and si have at least L-d+1 positions that share

the same alphabet, hence s and si have at most L-d

positions with the same alphabet, then according to the pigeonhole theorem there exists a position on

s

₁ that is

the same with si but differs from the farthest string s,

we take the complement of the alphabet on that position, then one of the complements must be the same with the alphabet on s, therefore that change will make the candidate string closer to the farthest string.

The change made in the FSD procedure will be made to recursively call (|Σ|-1) *(L-d)FSD procedures

3 Farthest String Defined by Maximum

Hamming Distance Sum

Since the term “farthest string” can be defined to either be restricted in a given string set or can be any arbitrary string constituted by the alphabet set.

Input: Strings s1, s2, . . . , skover alphabetΣof length L.

Question: Find a string s∈{s1, s2, . . . , sk} that

maximizes

∑

= k i i H

s

s

d

1

)

,

(

?

Given a set of k strings of length L, we can think of these strings as a k × L character matrix. Then we refer to the columns of this matrix as columns of the set of strings. Note that, given a set of length L strings S = {s1, s2, . . . , sk}, a created string with the largest

hamming distance can be easily computed by choosing in every column a letter occurring the least times. This way of selecting the letters is called the minority vote; yet this technique does not necessarily produce a unique solution.

Lemma 3. By using the minority vote technique to solve this problem still can not find the exact result.

Proof. We can to use the minority vote technique to find the pseudo farthest string, and then decide which existing string is closest to this string by computing the hamming distance sum. Yet, this algorithm does not yield a correct solution for two reasons. First, since the result of the minority vote technique is not unique. Selecting different alphabets can have different results. Secondly, when searching for a string that most

resembles the pseudo farthest string there may be more than one choice available. Apparently, this string does not yield the correct solution but an approximate result of the farthest sting bounded by the given string set problem.

Fig. 2 The result of using the minority vote technique, the output is “00”, we can see that “00”and “11”have the same hamming distance with the ideal solution”10”, therefore we choose the first choice “00”. But the best solution in this example is “11”, so we introduce the concept of weighted votes.

Let

num

( p

α

,

)

denote the number of times the

alphabet alpha appears on the pth column. We assign a weight on every alphabet in a column, which is defined as k subtract the times an alphabet appears in the column. Every different combination of alphabets will yield different weights, and selecting the string with the largest combined weight is then the solution of this problem. The weight of the pth position of the ith string is defined as

w

_i

[

p

]

=

k

−

num

(

s

_i

[

p

],

p

)

Theorem3.

∑

∑

= ≠

=

L p i i j j i H

s

s

w

p

d

1

]

[

)

,

(

Proof.

0 0

1

1

The number of 1’s in the first bit is the least of the candidates, so we choose 1 as the minority vote. The number of 0’s in the second bit is the least, so the minority vote is 0.

∑

∑

∑∑

∑∑

∑

= = = ≠ ≠ = ≠

=

−

=

=

=

L p i L p i L p j i j i H i j L p j i H i j j i H

p

w

p

p

s

num

k

p

s

p

s

d

p

s

p

s

d

s

s

d

1 1 1 1

]

[

)

],

[

(

])

[

],

[

(

])

[

],

[

(

)

,

(

In other words, the sum of the hamming distance of the ith string and the other strings in the set will equal the sum of weights of every position on the ith string. Algorithm Implementation

The concept of our algorithm is to calculate the weighted sum of every string and examine which string will yield the largest weighted sum, the designated string is then the solution to this problem.

1 for p=0 to L 2 for i=0 to k 3 num[si[p]] += 1 4 farthest = 0 5 farthest_distance = 0 6 for i=0 to k 7 temp_distance = 0 8 for p=0 to L 9 temp_distance += k - num[si[p]] 10 if temp_distance > farthest_distance 11 farthest_distance = temp_distance 12 farthest = i return sfarthest

Fig. 3 The above algorithm calculates the weighted sum of every string in the set, and selects the string with the largest sum.

Note that if the alphabet size is not binary and

exceeds the number k, in [6] it has been shown that it is possible to find an isomorphic mapping that transforms the set of strings into a set that uses at most k alphabets. Also note that, with slight modifications, the algorithm may be implemented to compute for a farthest string that does not necessarily be in the given set of strings.

Theorem 4 Given a set of binary strings S = { s1,

s2, . . . , sk }, the algorithm in figure 3 determines in

O(kL) time finding a string that maximizes

∑

= k i i H

s

s

d

1

)

,

(

. Proof.

Running time. The loops on line 1-3 will take O(kL)

loops and each loop takes O(1) time, and the same situation occurs on line 8-12. Rest of the pseudo-code takes O(1) time. Thus the upper bound on this algorithm is O(kL).

Correctness. By Theorem 3, the string with the maximum sum of weights is the string that we are searching for. The algorithm that we propose calculates the sum of weights for every string in the set, and selects the string with the maximum sum. Therefore, by Theorem 3 we indeed obtain the farthest string. Conclusion

In this paper we present two definitions in which the farthest string may be defined. Either via the maximum hamming distance sum between the set of given strings or via the minimum distance for a farthest string. We present algorithms to achieve the answer for both of these problems.

the minimum hamming distance d is a fixed constant. This result is very useful in the field of bio-information. Yet, still much effort is still needed. Although we have proved the algorithm to be linear, the coefficient of the algorithm may be very large depending on the value of d that we select. Ways to cut down on the coefficient of the algorithm will yield a better practical use of our algorithm.

References

[1] J. Alber, J. Gramm, and R. Niedermeier. Faster exact solutions for hard problems: a parameterized point of view. Discrete Mathematics 229:3-27, 2001.

[2] S. Arora, C. Lund, R. Motwani, M. Sudan, M.

Szegedy, Proof verification and

intractability of approximation problems, In Proceedings of the 33th Annual IEEE Symposium on Foundations of Computer Science, 13–22, 1992.

[3] R. G. Downey and M. R. Fellows. Parameterized Complexity. Springer-Verlag, New York, 1999.

[4] M. R. Fellows. Parameterized complexity: the main ideas and connections to practical computing. In Experimental Algorithmics,

Lecture Notes in Computer Science,

Springer-Verlag, Berlin, 51–77, 2002.

[5] M. Garey, D. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, San Francisco, 1979.

[6] J. Gramm, R. Niedermeier, and P. Rossmanith , Fixed-Parameter Algorithms for CLOSEST STRING and Related Problems, Algorithmica 37: 25–42, 2003.

[7] T. Jiang, C. Trendall, S. Wang, T. Wareham, X. Zhang, Drug target identification using Gibbs sampling techniques, in: Pacific Symposium on

Biocomputing, 389–400, 2000.

[8] J. K. Lanctot, M. Li , B. Ma, S. Wang, and L. Zhang, Distinguishing string selection problems, Information and Computation 185: 41–55, 2003.