New Group Shuffled BP Decoding Algorithms for LDPC Codes

ISIT2009,Seoul, Korea, June28 -July3, 2009

New Group Shuffled BP Decoding Algorithms for

LDPC Codes

Chi-Yuan Chang, Yu-Liang Chen, Chang-Ming Lee, and Yu T. Su

Department of Communications Engineering National Chiao Tung University

Hsinchu, 30056, TAIWAN

Emails:tofar.cm96g@nctu.edu.tw.ttttI415@gmail.com.cmlee.cm89g@nctu.edu.tw.ytsu@mail.nctu.edu.tw

Abstract- 1mplementing a belief propagation (BP) based LDPC decoder requires high degrees of parallelism using many com ponent soft-in soft-output (SISO) decoding units to perform message passing from variable nodes to check nodes or vice versa. An obvious complexity-reduction solution is to serialize the decoding process, i.e., dividing a decoding iteration into several serial sub-iterations in which a sub-iteration performs only part of the com plete parallel message-passing operation. The group horizontal shuffled BP (GHSBP) and vertical shuffled BP (GVSBP) algorithms respectively partition the check and variable nodes of the code graph into groups to perform group-by-group message-passing decoding. This paper proposes new techniques to improve three key elements of a GHSBP decoding algorithm, namely, the grouping method, the decoding schedule and the log-likelihood updating formulae. The (check nodes) grouping method and decoding schedule optimize certain design criterion. The new normalized min-sum updating formula with a self-adjustable correction (scaling) factor offers better nonlinear ap-proximation. Numerical performance of new GHSBP algorithms that include part or all three new techniques indicate that the combination of the proposed grouping and decoding schedule yields a faster convergence rate and our modified min-sum algorithm gives performance superior to that of the conventional min-sum and normalized min-sum algorithm and is very close to that of the sum-product algorithm.

I. INTRODUCTION

The belief propagation (BP) [4] or sum-product algorithm (SPA) is an efficient inference algorithm on trees and has demonstrated empirical success in numerous applications that involve loopy networks including LDPC codes and turbo codes. The algorithm is naturally suited for parallel processing but, except for short codes, hardware implementation of a parallel decoder requires large memory, high computational complexity and complicated interconnection. A more practical alternative is to partition either the variable nodes or the check nodes of the corresponding bipartite code graph into several groups and perform group-wise parallel decoding in a serial manner. Depending on which class of nodes are partitioned, these two parallel-serial approaches are referred to as the (group) horizontal shuffled BP (GHSBP) [10] [11] and the (group) vertical shuffled BP (GVSBP) algorithms [6]-[9], respectively. The group shuffled BP algorithms have the advantage of passing more reliable messages earlier for subse-quent iterative decoding. As a result, they reduce the number of iterations needed to achieve a predetermined performance. The min-sum algorithm (MSA) [12], which replaces the nonlinear check node operation,

-In tanh[Ei-In tanh(IXil/2) /2], by a single rmrnmum operation, was introduced to reduce the complexity of the standard BP algorithm at the cost of a noticeable degradation in the decoding performance. Some modifications are therefore proposed [13]-[15]. The normalized min-sum algorithm (NMSA) and the offset min-min-sum algorithm multiplies and adds a constant correction factor in the check-to-variable updating of MSA. They offer performance near that of the standard BP algorithm but with lower complexity. In this paper we introduce a partition-dependent parameter that measures the average degree of variable nodes in a group and present a new grouping method which has better average connection measure, i.e., it results in an increase of the average number of check nodes connected to a variable node in a group. This is achieved by allowing a check node to be in different groups whereas for the conventional grouping is a partition such that each check node belongs to one group only. An associated (group) decoding schedule that makes each subiteration to use most recently updated messages as soon as possible is proposed as well. The combination of grouping and scheduling enables our algorithm to outperform the stan-dard BP and GHSBP algorithm with the same computation complexity.

Besides new grouping and scheduling methods, we also propose a modified version of the normalized min-sum al-gorithm (M-NMSA) that takes into account the effect of the magnitude summation of variable-to-check messages on the nonlinear function mentioned above. The new approximation induces a self-adjustable correction factor in the corresponding node updating formula.

The paper is organized as follows. In Section II, we present some properties of the LDPC codes. In Section III, the new grouping method and the corresponding decoding schedule are presented. In Section IV, we describe our modified normalized min-sum algorithm and Section V provides some simulated numerical results about the performance of the proposed algorithms. Finally, conclusion remarks are drawn in Section VI.

II. SOME PROPERTIES OF THE LDPC CODES A regular binary (N, K) (dv , de) LDPC code Cis a linear block code described by an M x N parity check matrix H which has d; ones in each column and de ones in each

(1) row. H can be viewed as a bipartite graph with N variable

nodes corresponding to the encoded bits, and M check nodes corresponding to the parity-check functions represented by the rows ofH. The code rate of C is given by R

==

K / N.

Let N(m) be the set of variable nodes that participate in check node m and M(n) be the set of check nodes that are connected to variable node nin the code graph.N(m)\nis de-fined as the setN(m) with the variable nodenexcluded while

M(n)\m is the set M(n) with the check node m excluded. We further define W(m) as the union of M(n*), where

n* EN(m), i.e., W(m)

==

Un*EN(m)M(n*), and similarly, we defineU (

m)

as the set of variable nodes that participate in the check~odes inW(m), i.e., U(m)

==

Um*EW(m)N(m*). The following four properties on the cardinalities of W (m) and U(m) associated with a regular binary (N, K) _{(dv, de)}

LDPC code C are needed in our subsequent discourse. Property 1: For any check node m ofC, IW(m)1 ::;(dv

-1) .de

+

1.

Property 2:Ifm is a check node of C which is not involved in any cycle of length4,then IW(m)1

==

(dv - 1) .de

+

1.

Using the above two properties, we further obtain

Property 3: If the girth of C is greater than 4, then

IW(m)1

==

(dv - 1) .de

+

1 for every check nodem.

and

Property 4:For every check node m ofC, IU(m)1 ::;(dv

-1) .(d~ - de)

+

de.

III. GROUPING CHECK NODES AND DECODING SCHEDULE The conventional GHSBP and HSBP algorithms partition the check nodes into groups of equal cardinalities according to their natural order, that is, M checks of a codeword are divided into G groups, and each group contains M/ G

==

N; checks (assuming G

==

0 mod N for simplicity). Therefore, check nodes iN; to (i

+

l)Ne - 1 belong to the ith group,

i

==

0,1, ... ,G - 1.

Let Yi(P) be the ith group of check nodes resulted from a given partitionP, then the uniform partition of the conven-tional GHSBP algorithm Peon yields Yi(Peon)

==

{ml(iNe

<

m ::;(i

+

l)Ne-I}. Although for an uniform partition, each

check node belongs to a group only, and the variable nodes are likely to be connected to check nodes in more than one Yi(Peon).

When G

==

1,the GHSBP algorithm becomes the standard BP algorithm, and ifG

==

M, the GHSBP algorithm becomes the horizontal shuffled BP (HSBP) algorithm. The HSBP algorithm allows the more reliable (most recently updated) messages to be used as soon as they become available at the cost of a larger decoding delay due to its fully sequential nature. The GHSBP algorithm reduces the decoding delay with a parallel-serial message-passing approach but may lead to performance inferior to that of the HSBP algorithm.

We denote the set of variable nodes that participate the check nodes inYi(P) by

No..

i.e.,Ngi

==

Um*Eg.(p)N(m*), where we have omitted the dependence of the _~ets

No.

on the partition P for the sake of notational brevity. The ratio

~~~I represents the average number of check nodes connected

ISIT 2009, Seoul, Korea, June 28 - July 3,2009 TABLE I

MACKAY(504,252)REGULAR CODE,_{d v} = 3,de = 6 I Grouping Method Ec New N;

==

13 1.2187 Conventional N;

==

12 1.0368 Random N;

==

12 1.0438 Random N;

==

13 1.0494 Random Ne

==

14 1.0545 TABLE II

MACKAY(816,408)REGULAR CODE,_{d v} = 3,de = 6 I Grouping Method E_c New N;

==

13 1.1996 Conventional N;

==

12 1.0021 RandomN;

==

12 1.02615 Random N;

==

13 1.02973. Random Ne

==

14 1.03209.

to a variable node in Yi(P). Hence, a larger ~~~I means, on the average, the variable nodes in

No.

receivemessages from more check nodes and more reliable message will be forwarded from the variable nodes in

N

gi .Define the average check number (ACN) for a given partitionP as

C-l

Ec(P) =

~

L

Nc·dc

G i=O

INgil

A. A New Grouping Method

Let Pnew be the partition1(grouping) such that

Ym(Pn ew )

==

W(m), 0::; m

<

M - 1 (2)

Such a grouping method results in M groups with duplicate member nodes, i.e., a check node may belong to several groups.

Property 3immediately tells us that, for the above grouping method, N;

==

(dv - 1)de

+

1 if the girth of the code is

larger than 4. Table I and Table II list the ACN's (Ec(P))

for different grouping (partition) methods where the random grouping method refers to the method that select N; check nodes randomly for each group. The group sizes N; of other methods are chosen to be close to (dv - 1) . de

+

1 for fair comparison. The results indicate that the new grouping method offer ACN's larger than other grouping methods. This is partially due to fact that for the proposed grouping method

IN

giI

==

IU(m)Iis upper-bounded (see Property 4) while for other methods

IN

giImay be larger than (dv-l)(d~-de) +de.

B. A New Decoding Schedule

Having determined the grouping of check nodes, we now consider the associated group-decoding schedule. In order 1Such a "partition" is not really a partition anymore, whence to avoid abusing the term we will refer to it as grouping henceforth.

ISIT 2009, Seoul, Korea, June 28 - July 3, 2009

Initialization: Let 1/J

==

{lll ::; l ::;M - 1}, O(l)

==

0 for

o ::;

l ::; M - 1. Set i

==

1 and maximum number of iterations to IM a x . For each m,n, set Zn---+m

==

L(n).

Step 1: For j

==

1 :M - 1

that more reliable messages be used as soon as they become available, we schedule the group message-passing order in an iteration by 0(0) ----* 0(1) ----* ••• ----* O(M - 1), where O(j)

defined by (3) is the jth group to be processed. That is, having selected the 0(j - 1)th group to be processed, we assign the one which has not been processed and whose connecting variable nodes set U (0(j)) has the largest intersection with U (0(j - 1)) as the next group to be processed. Note that the indexes for the check node groups induced by a grouping method say, (2), and those associated with a decoding schedule is very likely to be different.

Assume a codeword C

==

[co,

Cl,... , CN-l] is BPSK-modulated and transmitted over an AWGN channel with noise variance (J"2. Let R

==

[ro, rl,...,rN-1] be the corresponding received sequence and L(n) be the log-likelihood ratio (LLR) of the variable node n with the initial value given by

L(n)

==

;2rn. Cm---+n denotes the check-to-variable message from check node m to variable node nand Zn---+m denotes the variable-to-check message from variable node n and to check node m. _z~i) represents the a posteriori LLR of the variable node n at the ith iteration. The proposed algorithm with the new grouping method and new scheduling of groups is carried out as follows.

Step 2: For k

==

0 : M - 1

Step 4: Hard decision and stopping criterion test: I Vertical Updating Method I Horizontal Updating

TABLE III

COMPARISON OF NORMALIZED UPDATING COMPLEXITIES

a) Create n(i)

==

[d6i),dii), ... ,dW-l] such that d~)

==

0 if z~i) ~ 0 and d~)

==

1 ifz~i)

<

o.

b) Ifn(i)HT

==

0 or I_{M a x} is reached, stop decoding and

outputn(i) as the decoded codeword. Otherwise, set i

==

i

+

1 and go to Step 2.

C. Computation Complexity

For the proposed algorithm, each decoding iteration consists of M subiterations and the number of check nodes in a group depends on d., d.; and the girth of the code. The GHSBP algorithm requires

l

M/ NcJ

<

M subiterations with no overlapping check node updating in an iteration while the BP algorithm processes all node updatings in parallel.

Table III shows the numbers of normalized (by the degrees of the nodes of concern) updatings per iteration for different algorithms. When the girth ofCis larger than 4, the inequali-ties in Table III will become equaliinequali-ties. Although the proposed algorithm has higher per-iteration computation complexity because of the overlapped grouping, its convergence speed and performance, as will be shown in Section V, are superior to those of the other two algorithms such that it outperforms BP and GHSBP with identical computation complexity constraint.

BP M N GHSBP M N New ::; M .(d v - 1) .de

+

M ::; N . (d v - 1) .de

+

N (3) argmax(IU(O(j-1)) nU(l)I), lE'ljJ ~ 1/J\ O(j) O(j) 1/J

(7) used in (8) brings about some performance degradation, hence several improved approximations were suggested. The normal-where sgn(x) is equal to the sign of the argumentx and

¢(x)

==

¢-1(x)

==

-In tanh(x/2) (5) b) Vertical Step: Vn E U(O(k

+

1)) if k

<

M - 1 or

n EU(O(O)) ifk

==

M - 1, and each m E M(n)

IV. MODIFICATIONS OF MIN-SUM ALGORITHM

(8) (9)

{ II

sgn(zn,---+m)} n'EN(m)\n X min IZn'---+ml. n'EN(m)\n Cm---+n

¢ {

L

¢(Izn,---+ml)}

~

min IZn'---+ml n'EN(m)\n n'EN(m)\n

The approximation

A. Min-Sum Algorithm and Normalized Min-Sum Algorithm For conventional BP or SPA, the horizontal updating, (4), (5), involves some nonlinear operations which can be sim-plified by approximating the composite nonlinearity in the horizontal step. The min-sum algorithm (MSA) is perhaps the most common simplification which replaces (4) by

(4)

(6)

Zn---+m

==

L(n)

+

L

Cm'---+n m'EM(n)\m

a) Horizontal Step: Vm EW(O(k)),n EU(O(k))

Cm---+n

{II

sgn(zn,---+m)} X n'EN(m)\n ¢ {

L

¢(Izn,---+ml)} n'EN(m)\n Step 3: V 0::; n ::; N - 1, z~i)

==

L(n)

+

L

Cm'---+n m'EM(n)

ISIT 2009, Seoul, Korea, June 28 - July 3, 2009

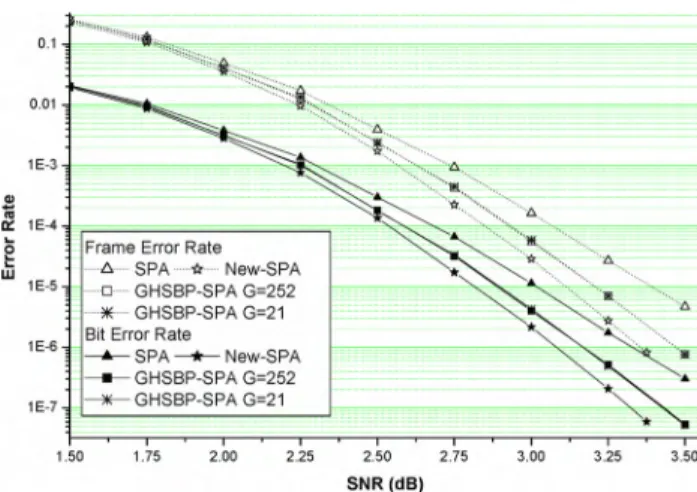
Fig. I. FER performance of Mackay's (504,252) regular LDPC code using GIISBP, and New-SPA and fully-parallel BP decodings.

ized min-sum algorithm (NMSA) scales (8) by a factor 0::

Cm-+ n = 0: {

II

sgn(zn,-+m)}

n'E.N(m)\n (10)

x

min IZn' -+ml.

n ' E.N(m )\n

where 0

<

0: ::::; 1.

B. Modified Normalized Min-Sum Algorithm

Let X , Y be two sets of positive numbers with the same cardinalityJ and assumex* and y* are the smallest number in X and Y,respectively. Since ¢(x)is a monotonic decreasing function for positive x, we have

(11) 0.01 1E-3 1E-4 1E-5 1E-6 1E-7 1.50 1.75 2.00 2.25 2.50 SNR (dB) 2.75 3.00 3.25 3.50 Define Define

where ,8

>

0 is an empirical scalar that ensures 0

<

0: ::::; 1. The resulting updating formula called the modified NMSA (M-NMSA), will have a variable correction factor that depends on

Zsum and Zmin.

It can be shown that ifx* = y* and X sum

<

Ysum then the

following inequality holds with high probability.

¢

(~ ¢(Xi))

<

¢

(~ ¢(Yi))

<

x* = y* (13)

V. SIMULATION RESULTS A. Notations and assumptions

The frame error rate (FER) and the bit error rate (BER) per-formance of various combinations of the grouping/scheduling method and the message-updating formula in decoding Mackay's (504,252) regular LOpe code [16] with de = 6, dv = 3 are examined. The frame duration is assumed to be equal to the codeword length, hence FER is actually the same as the codeword error probability. To distinguish these combinations we use the following shorthands. GHS-MSA,

B. Numerical examples

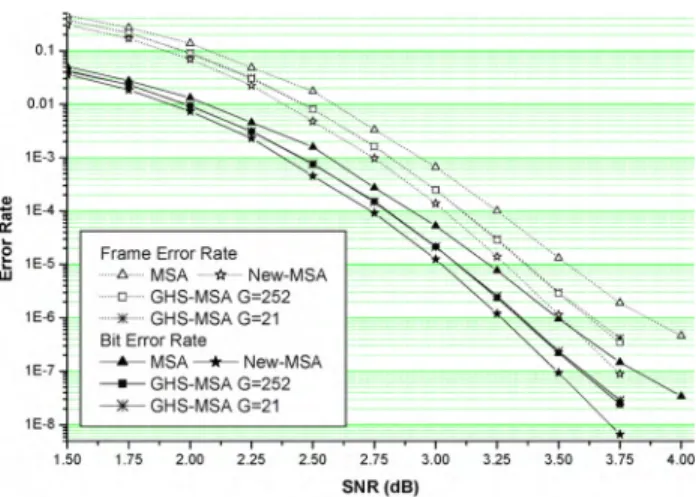
Fig. I depicts the FER and BER performance of the stan-dard BP algorithm, the GHSBP algorithm and the algorithm using the proposed grouping and scheduling. With the same computation complexity, our algorithm is about0.23 dB better than the standard BP algorithm at the FER ~ 10-4 _and outperforms the GHSBP algorithm with Ne = 12 (G = 21) by about 0.1 dB at the FER = 10-5 . Our algorithm provides better performance but requires less decoding delay because Ne = 13. Performance curves in Fig. 2 show that New-MSA is about 0.25 dB better than MSA at the FER = 10-4 _and outperforms GHS-MSA 0.12 dB at the FER = 10-5 .

Fig. 3 compares the FER performance of the MSA, the NMSA, the M-NMSA and the standard BP algorithm. [13] suggested 0: = 0.8 for the code with dv = 3 and de = 6 as the best scaling factor and we set ,8 = 1.1 for M-NMSA. The simulation results shows that M-NMSA gives FER performance better than that of NMSA and MSA under the same computation complexity constraint.

Fig. 4 compares the FER performance of the proposed algorithm using min-sum and its variations, i.e., performances of New-MSA, New-NMSA, New-M-NMSA and New-SPA are New-SPA, New-MSA, New-NMSA, and New-M-NMSA stand for the group horizontal shuffled min-sum algorithm and the GHS algorithm using the proposed grouping/scheduling method with SPA, MSA, NMSA and M-NMSA, respectively. If a shorthand contains no prefix, e.g., SPA, MSA, NMSA, M-NMSA, then the simulated decoding is assumed to be carried out with regular fully parallel processing.

The simulation results reported in this section assume IM a x = 50 for the proposed algorithms. In order to have a fair performance comparison with the conventional BP algorithm and the GHSBP algorithm under the same computation com-plexity, we set IM a x = 650 for the standard BP algorithm, the GHSBP algorithm, the min-sum algorithm and the GHS-MSA because of the complexity multiplicity (dv - 1) . de

+

1 = 13 shown in Table 111. (15) (16) (14) (12) Zm in 0: =1 ,8 · -Zsum

X sum = L Xi, Ysum= LYi

i i

Zmin = min IZn'-+ml

n ' E.N(m )\ n

Zsum = L IZn'-+ml n ' E.N(m) \n

(13) and the fact that only the minimum value Zmin is

con-sidered in(8) and (10) implies that in many cases when MSA and NMSA cannot distinguish between two sets of variable-to-check messages, Zsum can provide the information about

their relative magnitudes of updating messages computed at a check node. (13) then suggests that we modify the factor 0: in (10) as

ISIT 2009 , Seoul , Korea, June 28 - July 3, 2009

"·"·'t"••,..:

1.50 1.75 2.00 2.25 2.50 2.75 3.00 3.25 3.50 3.75 4.00

SNR(dB)

Fig. 4. FER performance of Mackay 's (504 ,252) regular LDP C code using New-MSA, New-N MSA, and New-M-NMSA and New-SPA.

given.

f3

= 1.1 is used in New-M-NMSA. The simulation curves indicate that NMSA is not suitable for use in conjunc-tion with the proposed grouping and scheduling and New-M-NMSA outperforms New-New-M-NMSA by about 0.12 dB at the FER

~5 x 10-5 .

VI. CO NC L USIO N

We have presented several new techniques to improve the performance of SPA and GHSBP algorithm for LDPC codes. The new grouping method is based on the ACN that measures the average degree of variable nodes within a group while the corresponding decoding schedule tries to use the newly updated messages as soon as they become available. Although the proposed grouping method results in multiple nodes-to-nodes message subiteration updates within each iteration, numerical results show that the increased complexity is more than compensated for by improved performance when used in conjunction with the proposed decoding schedule. That is, better performance is obtained with the same complexity.

To reduce the decoding complexity with minimum or no performance degradation, we also propose a modifi cation of the normalized min-sum algorithm with a self-adjustable correction factor that take into account the information pro-vided by the sum of variabl e-to-check messages. Simulated performance indicate that the new updating formula gives the FER performance almost as good as that of the classic SPA.

RE FEREN CES

[II R. G. Gallager,Low-density parity- check codes, Ca mbridge, MA: M.I.T

Press , 1963.

[2] D. J. C. Mac Kay and R. M. Neal, "N ear Shannon limit performance of low den sity par ity check codes ," Electronics Lell., vol. 32, no. 18, pp.

1645-1646, Aug . 1996.

[3] D. J. C. MacKay, "Good error-correcting codes based on very sparse matrices," IEEE Trans. In! Theory, vol. 45, pp. 399 -431 , Mar. 1999.

[4] Pearl, J., Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inf erence, San Mateo , CA: Morgan Kaufmann, 1998.

[51 R. M. Tann er, "A recur sive app roach to low complexity codes," IEEE Trans. Inf Theory, vol. IT-27, pp. 533-547, Sept. 1981.

[6] 1. Zhang and M. Fossorier, " Shuffled belief propagation decoding," in

Proc. 36th Annu. Asilomar Con! Signals, Syst., Computers, pp. 8-15 ,

Nov. 2002.

[7] J. Zh ang and M.P.C. Fossorier, " Shuffled iterative decodin g," IEEE Trans. Commun., vo1.53, no.2, pp.209-21 3, Feb. 2005 .

[8] 1. Zhang, Y. Wang, and M.P. C. Fossorier, 1. S. Yedidia, " Replica shuffled iterative decoding,"Proc. 2005 IEEE Int. Symp. on Iriformation Theory, pp. 454V 458 , Adelaide, Austra ilia, Sept. 2005 .

[9] 1. Zhang, Y. Wang, and M.P. C. Fossorier, 1. S. Yedidia, " Iterative decoding with repl ica," IEEE Trans. Inform. Theory, vo1.53, no.5 ,

pp.I644-1 663, May 200 7.

[10] E. Yeo,1'. Pakzad , B. Nikolic, V. Anantharam, " High throughput low-dens ity parity-ch eck decoder architecture s," inProc. GLOBECOM '01"

pp. 301 9-3024 , Nov. 200I.

[III A. Segard, F. Verdier, D. Declercq and1'. Urard, "A DVB-S2 compliant LDP C decoder integrating the horiz ontal shuffle schedule," inISPACS

'06.,pp. 1013-1016, Dec. 2006 .

[12] M.P. C. Fossorier, M. J. Mihaljevic and H. Imai, " Reduced compl exity iterative decodin g of low-d ensity parity check codes based on belief propagation," IEEE Trans. Commun., vol. 47 pp. 673-680, May, 1999.

[13] 1. Chen and M.P. C. Foss orier, " Density evolution for two improved BP-Base d decod ing algorithms of LDPC code s," IEEE Commun. Lett.,

vol. 6 pp. 208 -210 , May, 2002 .

[14] J. Chen and M.P. C. Fossorier, "Ncar optimum universal belief propagation based decoding of low-densit y parity-ch eck cod es," IEEE Trans. Commun., vol. 50, pp. 406-414, Mar. 2002.

[15] J. Chen, A. Dholakia, E. Eleftheriou, M. P. C. Fossorier, and X.-Y. Hu, " Reduced-complexity decoding of LDPC codes ,"IEEE Trans. Commun.,

vol. 53, pp. 1288-1299, Aug. 2005 .

[16] D. 1. C. MacKay,Encyclopedia of sparse graph codes [Online].

Availi-ble: http ://www.inference.phy.cam .ac.uk/mackay/codes/data.html

..

"IJ.-..

3.25 3.25 3.00 .... "", " . ' ", 3.00 2.75 ... 2.75 2.50 2.50 SNR(dB) SNR (dB) 2.25 2.25 2.00 2.00 1.75 1.75 ~ ~ :~. ~.,.. .~~ ~.;:::~", ~:~_{.~ ',~} t~~~:"_~ ... '..""-, i0., - , "<. t~. "'" ~,,,

'""", 0",.:--"

.'''~.'

""

..

~ - y- MSA

"

I~~-- ,"I~~-- SPA -... NMSA,a=O.8 .~ - e- NMSA,a=O.71 _{,-""","-.: .} - . - M-NMSA, p=1.1 1.50 lE-5 1.50 y New-MSA ... J< New-SPA

lE-5 - New-NMSA,a=O.8

*

New-M-NMSA, p=1 1 ...• ... lE-4i --;=========;---"···,~·~~-· -0.1 J!!

..

0.01 t>: ~ ~ W 1E-3

..

E l! U. 1E-4 0.01 -J - - - ...:c"···' : $: :·.:••·..."... -~ 0.1 ,..""' ;.; ; .::::::c,_.~_~_ _~~ ~~~~~_ _ ", ...,.. ...::::;;:;;:: . "

.

~ lE-3~ ---'···.:::c.,.--::c~ ,---­

w

_..

E e u.

Fig. 2. FER performance of Mackay (504 ,252) regular LDP C cod e using the decod ing algorithm s: GHS-MSA, New-MSA and fully parallel MSA.

Fig. 3. FER performance of Macka y's (504 ,252) regular LDPC code using the decod ing algorithm s: MSA, NMSA, M-NMSA, and BP.