Internal Solitons in the Northeastern South China Sea
Part I: Sources and Deep Water Propagation
Steven R. Ramp, Tswen Yung Tang, Timothy F. Duda, James F. Lynch, Senior Member, IEEE, Antony K. Liu,
Ching-Sang Chiu, Frederick L. Bahr, Hyoung-Rok Kim, and Ying-Jang Yang
Abstract—A moored array of current, temperature, conduc-tivity, and pressure sensors was deployed across the Chinese continental shelf and slope in support of the Asian Seas Interna-tional Acoustics Experiment. The goal of the observations was to quantify the water column variability in order to understand the along- and across-shore low-frequency acoustic propagation in shallow water. The moorings were deployed from April 21–May 19, 2001 and sampled at 1–5 min intervals to capture the full range of temporal variability without aliasing the internal wave field. The dominant oceanographic signal by far was in fact the highly nonlinear internal waves (or solitons) which were generated near the Batan Islands in the Luzon Strait and propagated 485 km across deep water to the observation region. Dubbed trans-basin waves, to distinguish them from other, smaller nonlinear waves generated locally near the shelf break, these waves had amplitudes ranging from 29 to greater than 140 m and were among the largest such waves ever observed in the world’s oceans. The waves arrived at the most offshore mooring in two clusters lasting 7–8 days each separated by five days when no waves were observed. Within each cluster, two types of waves arrived which have been named type-a and type-b. The type-a waves had greater amplitude than the type-b waves and arrived with remarkable regularity at the same time each day, 24 h apart. The type-b waves were weaker than the type-a waves, arrived an hour later each day, and generally consisted of a single soliton growing out of the center of the wave packet. Comparison with modeled barotropic tides from the generation region revealed that: 1) The two clusters were generated around the time of the spring tides in the Luzon strait; and 2) The type-a waves were generated on the strong side of the diurnal inequality while the type-b waves were generated on the weaker beat. The position of the Kuroshio intrusion into the Luzon Strait may modulate the strength of the waves being produced. As the waves shoaled, the huge lead solitons first split into two solitons then merged together into a broad region of thermocline depres-sion at depths less than 120 m. Elevation waves sprang up behind them as they continued to propagate onshore. The elevation waves also grew out of regions where the locally-generated internal tide forced the main thermocline down near the bottom. The “critical
Manuscript received June 6, 2003; revised April 2, 2004. The planning, execution, and analysis of this work was supported by the U.S. Office of Naval Research Ocean Acoustics and Physical Oceanography Programs. Significant funding contributions were also made by the National Science Council of Taiwan.
S. R. Ramp, C.-S. Chiu, and F. L. Bahr are with the Department of Oceanog-raphy, Naval Postgraduate School, Monterey, CA 93943 USA.
T. Y. Tang is with the Institute of Oceanography, National Taiwan University, Taipei, ROC.
H.-R. Kim was with the Department of Oceanography, Naval Postgraduate School, Monterey, CA 93943 USA. He is now at Seoul National University, Seoul, South Korea.
T. F. Duda and J. F. Lynch are with the Woods Hole Oceanographic Institution, Woods Hole, MA 02543 USA.
A. K. Liu is with the NASA Goddard Space Flight Center, Greenbelt, MD 20771 USA.
Y.-J. Yang is with the Chinese Naval Academy, Kaohsiung, Taiwan, ROC. Digital Object Identifier 10.1109/JOE.2004.840839
point” where the upper and lower layers were equal was a good indicator of when the depression or elevation waves would form, however this was not a static point, but rather varied in both space and time according to the presence or absence of the internal tides and the incoming trans-basin waves themselves.
Index Terms—Baroclinic tides, nonlinear internal waves, ocean currents.
I. INTRODUCTION A. The ASIAEX Program
T
HE Asian Seas International Acoustics Experiment (ASIAEX) was a major field effort in coupled physical oceanography, geophysics, and environmental acoustics which took place during the consecutive springs of 2000 and 2001 in the South and East China Seas. The program was divided into two major components, a volume interaction experiment in the South China Sea (SCS), with Taiwan and Singapore as the primary collaborators, and a boundary interaction experiment in the East China Sea (ECS), with the People’s Republic of China (PRC) and Korea as the primary international partners. The overarching goal of the SCS volume interaction experiment was to understand acoustic propagation through shallow waterwhen strong oceanic variability in the form of fronts, eddies, boundary layers, and internal waves, is present. The goal of the
boundary interaction experiment was to develop models that
can predict the mean reverberation level and fluctuations using measured environmental parameters. Both experiments were
multiship operations and required close cooperation between acousticians, physical oceanographers, and geophysicists. All the partnering nations contributed human and financial resources to the program, which allowed a larger and more comprehensive experiment than would otherwise have been possible. This paper presents results from the SCS volume interaction experiment. Results from the ECS program are presented elsewhere in this special issue.
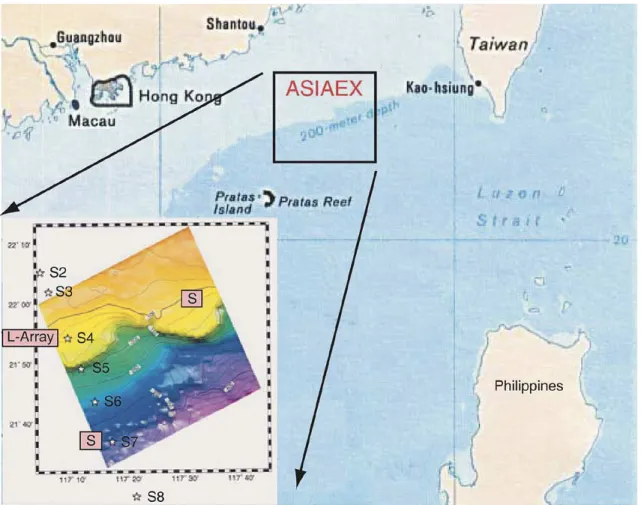
The science plan for the 2001 SCS experiment called for si-multaneous observations of the water column properties (tem-perature, salinity, and velocity) and acoustic propagation char-acteristics at very high resolution in space and time. This was accomplished by a combination of moored and shipboard obser-vations near the continental shelf break between the southern tip of Taiwan and Dongsha Island (also called Pratis Reef) bounded by 21 to 22.5 N, 117 to 119 E (Fig. 1). The moored array con-sisted of seven densely instrumented oceanographic moorings (S8–S2) deployed in an across-shelf line spanning 800 to 72 m
Fig. 1. Locator map showing the positions of the ASIAEX moorings. The current meter moorings are indicated by stars labeled S2–S8. The shaded red boxes indicate acoustic assets, with an “S” indicating sources and “L-Array” the horizontal and vertical receiving arrays.
(Fig. 1). These moorings were designed to be along the pri-mary acoustic transmission paths. Two sound sources operating at 224 and 400 Hz were deployed on the 350 m isobath and sources operating at 300, 400, and 500 Hz were deployed on the 120 m isobath (Fig. 1). The acoustic signals were all received at an L-shaped hydrophone array with both horizontal and ver-tical apertures, also moored on the 120 m isobath. While the acoustics results are not explicitly discussed in this paper, the mooring locations are included to foster comparisons presented elsewhere [1], [2].
While the moorings were in the water, shipboard surveys continuously mapped the area to ascertain the three-dimen-sional spatial scales and representativeness of the moorings. On the OCEAN RESEARCHER 1 (OR1), two surveys were conducted using the SeaSoar towed undulating vehicle: The small-scale SeaSoar survey mapped the three-dimensional water mass properties in the insonified region and a larger-scale survey described the surrounding mesoscale variability [3]. A second vessel, the OCEAN RESEARCHER 3 (OR3) steamed dedicated cruise tracks in the vicinity of the acoustic transmis-sion paths [4]. Both vessels collected temperature, conductivity, and hull-mounted ADCP velocity data as a function of pressure (depth). The SeaSoar aboard OR1 additionally sampled flu-orescence, bioluminescence, and light transmission while the OR3 sampled high frequency acoustic backscatter at 200 and
350 kHz for flow visualization of internal waves and evaluation of turbulence.
This manuscript focuses on results from the SCS program during spring 2001, with occasional reach-back to spring 2000 for critical supporting information. The primary analysis con-cerns internal wave variability as derived from the moored ob-servations of current, temperature, and salinity. A rich field of strongly nonlinear internal solitary waves (solitons) was ob-served from several different platforms during the course of the experiment. This paper identifies the basic characteristics of the waves, their sources, and their propagation characteristics. The tidal, mesoscale, and interannual variability are mentioned only peripherally as they pertain to understanding the internal wave dynamics. These lower-frequency motions are the primary focus of several other manuscripts in this volume.
B. Location and Basin Geometry
The South China Sea is one of a chain of marginal seas along the western Pacific Ocean. It fits into the chain between the In-donesian Seas to the south and the East China Sea, Japan (East) Sea, and the Okhotsk Sea to the north. The sea can be generally characterized as a deep ( m) basin bordered by a broad (220 km), shallow ( m) continental shelf to the north and west and a tropical island chain with almost no continental shelf to the south. The SCS is connected to the surrounding seas and
the open north Pacific (the Philippine Sea) by a number of straits with varying width and depth. Clearly the most important one is the Luzon strait located between Taiwan and the Island of Luzon in the Philippines, with a sill depth of about 1900 m. Most of the transport into the SCS comes from this strait, as does all of the ventilation in the SCS deep basin. There are several small island groups within the Luzon strait, some of which have very small, shallow passages between islands. These islands do not appre-ciably inhibit the mass transport through the strait, but may be important to the local dynamics as the generation point for the internal solitons observed propagating across the northeastern corner of the sea [5]–[7]. In the northeast sector of the SCS, be-tween the Luzon Strait and ASIAEX region, the central basin is more than 4000 m deep with no islands, banks, or other shallow spots in between. The Taiwan Strait lies between the Chinese mainland and the island of Taiwan. The mass transport through this shallow (60 m), narrow (140 km) strait is limited [8]. Its im-portance to ASIAEX lies in its amplification of the semidiurnal tide and introduction of fresh water to the region. This forcing and the resulting fronts and stratification do impact the acoustic propagation. The remaining connections between the SCS and its neighboring seas and basins are all too narrow or shallow to allow appreciable volume transport. They are quite distant from the ASIAEX region and have no discernable impact on the ob-servational results reported here.
C. Forcing by Wind
The SCS wind forcing is dominated by a summer monsoon which blows from the southwest to northeast, and a winter monsoon of opposite sign. In contrast to the well known Indian Ocean monsoon, the northeast (winter) monsoon in the SCS is the stronger one and dominates the annual statistics. The summer SW monsoon develops in June, reaches a maximum (order 0.15 Pa) in August, and begins to weaken in September [9]. In October, the transition to NE winds begins in the northern part of the basin and spreads southward, reaching maximum force (order 0.3 Pa) in December through March. April and May are transition months with the calmest seas, which influenced the timing of the ASIAEX experiments. A wild-card in the ASIAEX planning was the formation of mon-soon depressions which can sometimes develop into tropical cyclones. On average, about four monsoon depressions form per year between May and September, most frequently during August to September. May 2001 was unusual in that a weak tropical cyclone did occur. This storm was initially headed directly toward the ASIAEX region and several research ves-sels at sea, but the eye fortunately veered NE into the Luzon Strait on May 12 and did not pass through the ASIAEX box. Anomalous surface wind stress which resulted from the storm did impact the moored data, particularly the moorings in less than 80 m of water.
An important consequence of the monsoon variability is the presence or absence of the Kuroshio Current in the northeastern South China Sea. The Kuroshio stems from the North Equato-rial Current and flows northwest along the Philippines, across the Luzon Strait on the Pacific side, and continues along the south coast of Taiwan. Sometimes, however, the current en-ters the SCS via the southern portion of the Luzon Strait, loops
through the northeast corner of the sea, and then exits again via the northern Luzon Strait. The character of this “Kuroshio Intru-sion” (KI) is intermittent and highly seasonal. Most of the inflow occurs in fall and winter when it is supported by the NE mon-soon, which lowers the sea level/pressure head inside the SCS and encourages the intrusion to enter. Numerical models [10] produce an intrusion in the winter but not in the summer. Obser-vations are sparse but also show greater incursions of Kuroshio water during winter than summer [11]. The nature of the KI within the SCS is also variable. The current may retroflect en-tirely and leave the sea via the northern Luzon Strait. It may also bifurcate at the shelf break, with some water leaving and some turning southwest along the continental slope. This current is traceable along the entire shelf as a salinity maximum near 150 m depth over the slope. Finally, the KI loop current will oc-casionally detach and form a large warm core ring which prop-agates WSW into the sea. The importance of these processes for this paper is that the flow across the sills in the Luzon Strait depends strongly on the position of the Kuroshio is doing. The total flow, tidal plus mesoscale currents, determines how and when the internal solitons will be generated. The mean currents in the northeast SCS will also impact the apparent propagation speed of the internal waves as they move WNW from the gen-erating sills to the observation point on the Chinese continental shelf.
D. Tides
The barotropic tidal waves for both the M2 and K1 tides enter the SCS through the Luzon Strait and travel rapidly southwest-ward down the basin [12]. Upon striking the Sunda Shelf, to-pographic effects become important and refract the tidal waves both left and right into the Gulf of Thailand and the Java Sea. The strongest semidiurnal tides in the SCS are observed in the NE corner near the Taiwan Strait [13]. The amplitude of the M2 tide does not increase southward in the open water (20 cm ev-erywhere) but K1 does (20 to 40 cm). This is very unusual for such low latitudes and is because the whole basin may have a natural period quite close to diurnal [14]. The Gulfs of Tonkin and Thailand are very nearly quarter-wave resonators for the K1 tide which leads to very strong diurnal amplification in these re-gions. The tides throughout the basin are thus mixed, with some regions (the far north and off Borneo and Vietnam) being domi-nated by the M2 tide and other regions (open water and the two gulfs) being dominated by the K1.
E. Internal Waves
As observational techniques have improved and scientists have moved toward ever faster sampling speeds, internal waves have emerged as ubiquitous on the world’s continental shelves, in marginal seas, and near straits and restrictions where high-speed flow occurs. The South China Sea is no exception: Synthetic Aperture Radar (SAR) imagery [7], [15] and moored Doppler profilers and thermistor chains [5] and [6] have re-vealed strong nonlinear internal waves or solitons present in the northeastern SCS between Luzon Strait and the Chinese continental shelf, propagating slightly north of due west. The SCS pilot study moorings [16] clearly observed these motions,
and they influenced the design of the moorings for the main field program.
The study of internal waves has been generally divided among the generation, propagation, and dissipation problems. As will be seen, the generation region for the waves (the Luzon Strait) can be deduced from the ASIAEX observations, but save for the satellite remote sensing, there were no observations conducted there. There are many instances in the literature associating the generation of strong nonlinear internal waves with sills, straits, and abrupt topography, for instance in the Mediterranean [17], [18] fjord-like structures [18], [19] and at continental shelf breaks [21]–[24]. Generation is most often attributed in some way to tidal flow across abrupt topography [19], [20], [25]–[27] and the ASIAEX waves would appear to fit this description. Lacking in situ information at the generation site to describe the dynamics, this manuscript will focus mainly on describing the wave propagation through deep water and their transformation as they enter the shallower water over the continental shelf and slope. Wave generation will be discussed to the extent possible using a global tidal model for the gener-ation region.
The propagation of small or moderate amplitude solitary waves has been well described by two-layer Korteweg-de Vries (KdV) theory [28]–[31]. The waves evolve into the classic hyperbolic secant-squared shape as a balance between nonlinear effects and dispersion. Continuous stratification has been included in the problem by decomposing the particle velocities (u, v, and w) and wave displacements into a linear combination of vertical modes [23], [26], [32]. Recently, other lesser-known solutions to the KdV equation have been pursued (cnoidal and dnoidal) which produce many of the observed characteristics of solitary wave packets much better than the solution [23], [33]. The dnoidal solution, for instance, reproduces the rank-ordered nature of the wave packets and the trailing thermocline depression they leave behind.
When solitary waves enter shoal water, the upper and lower layer depths become nearly equal, the first-order nonlinearity term in the KdV equation goes to zero, and second-order nonlinearity must be invoked to balance wave dispersion [32], [34]. The simple KdV theory produces unrealistic results in this case and the second-order or extended KdV (EKdV) theory is needed. The KdV solution for instance produces wave am-plitudes which continue to grow as the water shoals, whereas the EKdV result provides amplitudes which first grow but then diminish in accordance with the observations. Two-dimensional horizontal solutions (x, y, z) are required to understand wave refraction by topography and radial spreading [35], [36]. This paper will consider observational results from a single linear mooring line approximately normal to the continental shelf break and will not attempt to address the two-dimensional results. Ultimately, the wave energy must be dissipated on the Chinese continental shelf via friction, refraction, wave breaking, and radial spreading [27], [35], [37]. These processes are better described by the ASIAEX Low-Cost (LOCO) Moor-ings located further onshore and are the focus of other ASIAEX papers [2], [4].
Of all the major sea-going internal wave studies to date, the one most closely resembling the ASIAEX configuration was
the Sulu Sea study conducted during May 1980 from the R/V OCEANOGRAPHER [26], [35]. The season, stratification, lon-gitude, and basin configuration together allowed the waves to travel great distances over deep water before shoaling on the other side, and were all quite similar to the situation presented in the northeastern South China Sea. At the time of their study, the wave amplitudes, associated wave velocities, distance trav-eled, and lifetimes were among the largest ever observed. Good agreement was found between the observed wave characteristics and modal solutions to a finite-depth version of the KdV equa-tion [38], [39]. The South China Sea waves were actually larger and propagated farther than the Sulu Sea waves. The waves in both regions were parametrically similar in some ways but dif-ferent in others, and extensive comparisons with the Sula Sea results will be made as this paper goes along.
II. DATA ANDMETHODS
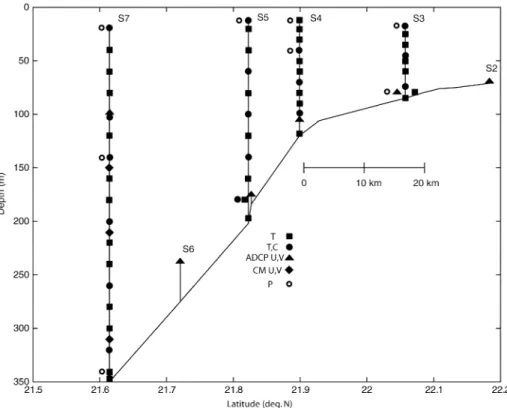
The primary instruments deployed on the physical oceanog-raphy (PO) moorings were temperature (T) pods; temperature and pressure (TP) sensors; temperature, conductivity, and pres-sure (TCP) sensors; and several generations of acoustic Doppler current profilers (ADCP’s) operating at different frequencies ac-cording to the range desired (Fig. 2, Table I). One mooring on the 350 m isobath had three additional Aanderaa RCM8 current meters below the ADCP to sample the deeper currents over the continental slope. The nomenclature S1-S8 has been adopted for the moorings, with S2–S8 forming the across-shore line and S1 located off to the northeast along the 80 m isobath. Fishing activity was intense in the area but the mooring survival rate was excellent under the circumstances. Mooring S1 was lost, the ADCP on mooring S8 did not function, and mooring S3 was sliced in half and dragged by fishermen. The upper half of the mooring was recovered after visual sighting by the OR1, and the bottom half was recovered by dragging during the final cruise on the OR1. Thus, a mostly complete data set was recovered along the main line spanning 72 to 350 m depth (S2–S7).
Anticipating an active internal wave field from the spring 2000 results, all instruments were set to sample as fast as possible within the constraints of instrument power and internal memory. The T, TP, and TCP sensors collected discrete samples at one-minute intervals (some at two-minutes) and the ADCP’s pinged continuously at one-second intervals, recording en-semble averages every one or two minutes. For those sampling at one minute, additional memory and external battery packs were installed to facilitate this sampling rate over one month’s time. The bin length was 10 m for the 150 kHz broadband ADCP at S6; 8 m for the 150 kHz narrowband at S5; and 4 m for the 300 kHz broadbands at the other moorings (Table I). The Aanderaa current meters recorded 2-min vector averages and seemed to work well despite the difficult conditions resulting from the high currents associated with the internal waves. The near-bottom SBE26 pressure gauges sampled at 5-min intervals which was more than adequate to sample the barotropic tide. The T, TP and TCP instruments were calibrated both before and after the experiment by the manufacturer.
To facilitate this analysis, the time series were digitally fil-tered into three bands; the internal wave (IW) band, the tidal (T)
Fig. 2. Cross-section of the oceanographic moorings showing the placement of the temperature, temperature/conductivity, pressure, current meter, and ADCP instruments in the water column.
band, and the low-frequency (LF) or mesoscale band. The data were first run through a well-known low-pass filter originating at Oregon State University [40] with a half-power point at forty-six hours. This filter does an excellent job of separating the tidal, inertial, and higher-frequency motions from the mesoscale vari-ability. The low-passed data were then subtracted from the orig-inal time series to remove the low frequency content, including the mean value. This intermediate time series was subsequently filtered again in frequency space to separate the internal waves from the tidal and inertial motions. The Fourier coefficients for periods shorter than 5 h were removed and the series were inverse-transformed to produce the band-passed times series, which were in turn subtracted from the intermediate series to produce the high-passed series. This technique was used in lieu of time-space filtering due to the enormous internal wave spikes which were not adequately attenuated using the usual convolu-tion methods. The resulting time series thus spanned less than 46 hours (LF), 46–5 h (T), and 5 h and above (IW). Little at-tention is paid in this paper to inertial motions, but it is worth noting here that the inertial period at 22 N is 32 hours so that both the semidiurnal and diurnal internal tides were superiner-tial, i.e., within the freely propagating internal wave band.
III. RESULTS A. Oceanographic Context
The emphasis in this manuscript is on describing and under-standing the internal waves, however some knowledge of the background flows and their relative strengths is useful to un-derstand certain features of the wave observations. At depths of 150 m and greater over the continental slope, the mean flow closely followed the topography toward the southwest at around
10 cm s with a low frequency standard deviation of about 6 cm s . At shallower depths, there was an increasingly on-shore component to the month-long mean. These currents had a subsurface maximum of about 15 cm s near 100 m depth at mooring S5. There was no hint of the northeastward-flowing South China Sea Warm Current (SCSWC), nor were there any major Kuroshio intrusions [3]. On the continental shelf inshore of mooring S4, the low-frequency standard deviations (15 cm s ) exceeded the mean flows ( cm s ) indicating that the mean flows on the shelf were not well resolved by these short records. This time period resembled the inter-monsoon, rather than the late-winter monsoon like in April 2000 [3]. The pri-mary utility of the mean currents for this paper lies in the ad-vection and background shear they present to the internal wave field. The vertical shear perhaps accounts for some of the vari-ability in the observed internal wave propagation speeds dis-cussed subsequently.
The mean currents in the tidal band were enormously com-plex indicating that there was significant baroclinic energy at these frequencies. This was particularly true at the slope moor-ings (S5-S7) where the tidal ellipses displayed a variety of sizes and orientations as a function of depth. The tides on the shelf were more organized. Statistically speaking, the current mag-nitudes in the tidal band ranged from 40 to 60 cm s across the entire array with standard deviations from 15 to 22 cm s , much stronger than the mean currents yet much weaker than the internal waves. The tides are the subject of two related manu-scripts in this volume on the barotropic [41] and baroclinic [2] tides. Noteworthy here is the relationship between the internal tide (period 12–24 h) and the observed large amplitude internal waves (period minutes to 2 h). Isolated packets of large ampli-tude, nonlinear internal waves have been referred to as solitons.
TABLE I
MOORINGLOCATIONS ANDINSTRUMENTDEPTHS FORALL THEENVIRONMENTALMOORINGSDEPLOYEDDURINGASIAEX, APRIL–MAY2001.
FOREACHADCP,THEFREQUENCY OFOPERATION, BROADBAND(BB)ORNARROWBAND(NB),ANDDEPTHCELLLENGTH(m) ISINDICATED.
THEADCPATSITE5 WAS ONITSOWNMOORING(S5a). THEREST OF THETABLEISSELF-EXPLANATORY
The internal tide itself has been referred to as an undular bore when it is particularly strong. When the solitons ride on the leading edge of an undular bore, they are called solibores. In this manuscript, we shall henceforth refer to the waves as soli-tons (or packets of solisoli-tons), because in the ASIAEX region they were usually but not always associated with the undular bore at tidal frequencies. Perhaps they began life that way, but evolved into soliton packets as they traveled the great distance (485 km) between the source region and the point of observa-tion. More observations are needed in the source and propaga-tion regions to understand this point. We return to the relapropaga-tion- relation-ship between the internal tide and the ASIAEX solitons later on in the paper.
Clearly, the most powerful motions contained in the data were observed in the internal wave band. The maximum currents of
( cm s ) at S7 for the (u, v) components were far stronger than the currents in the tidal or low frequency bands. The total flow in the upper layer due to the waves routinely exceeded 120 cm s at this mooring. At moorings S6 and S5 the IW currents were about double the tidal and low-fre-quency flows. From S4 on in, the IW and tidal currents had about the same magnitude, both stronger than the means. The internal waves statistically had opposing currents in the upper and lower layers around a nodal point whose depth varied be-tween moorings. The nodal point statistically fell near 140 m at S7 and 100 m at S6 and S5. Further inshore there was much tem-poral variation and the nodal point varied from wave to wave. Some case studies of the modal structure of individual waves is presented later. The statistics provide a snapshot summary of the internal wave variance which is impressive in its own right.
TABLE I
MOORINGLOCATIONS ANDINSTRUMENTDEPTHS FORALL THEENVIRONMENTALMOORINGSDEPLOYEDDURINGASIAEX, APRIL–MAY2001.
FOREACHADCP,THEFREQUENCY OFOPERATION, BROADBAND(BB)ORNARROWBAND(NB),ANDDEPTHCELLLENGTH(m) ISINDICATED.
THEADCPATSITE5 WAS ONITSOWNMOORING(S5a). THEREST OF THETABLEISSELF-EXPLANATORY
These were among the largest internal waves ever observed in the ocean.
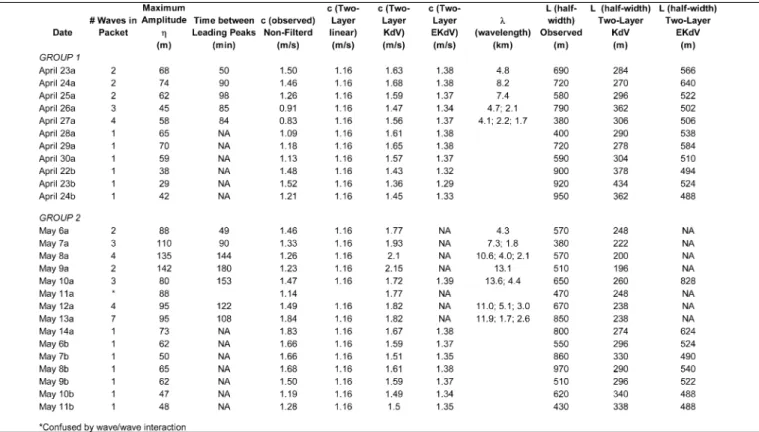
B. A Basic Description of the Internal Wave Arrivals
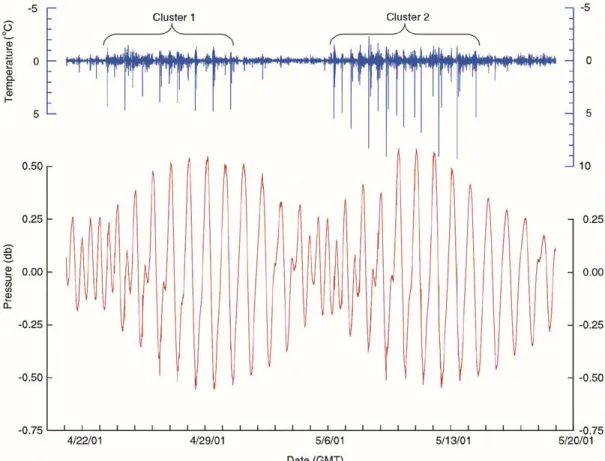
An overall impression of the scale of the internal solitons and when they occurred in relation to the local barotropic tide can be obtained by comparing the temperature fluctuations in the main thermocline with bottom pressure at mooring S7 (Fig. 3). The tide (red line) was mixed, diurnal dominant, with a large diurnal inequality and fortnightly variation. The tide was semi-diurnal at neap, then became increasingly mixed and was purely diurnal during four to five days around the time of the spring tide. The principal tidal constituents from a harmonic analysis (Table II) bear this out: The strongest components were the O1, K1, and M2 tides with amplitudes of 24, 25, and 13 cm, respectively.
The temperature fluctuations at 140 m (blue line) provide a robust indicator of when the internal solitons passed by the mooring. The waves were all depression waves at the 350 m isobath, such that each passing wave caused a pronounced in-crease in temperature as the thermocline moved sharply down past the sensor. Each “spike” in Fig. 3 actually consisted of a packet of waves which are not visible when plotted on this scale (see next paragraph). The term “cluster” as used in this
paper refers collectively to all the internal waves arriving on a certain phase of the barotropic tide, as indicated on the figure. Two such clusters of soliton packets were observed that had a counter-intuitive phase relationship with respect to the local fortnightly tidal beat. Recognizing that the waves were not lo-cally generated, this relationship is described first and the phase issue will be revisited after the wave sources and propagation have been discussed. The local observation was that the soli-tons first appeared during the neap tide, for instance on April 23 for the first cluster and May 6 for the second. For the first cluster, the temperature fluctuations induced were nearly con-stant at around 5 C across the entire cluster. For the second cluster, the temperature fluctuation increased from 5–9 C from May 6–9, with the largest waves occurring 2–4 days into the cluster on May 8 and 9. Two days of somewhat smaller waves were observed on May 10–11, followed by larger ( C) waves again on May 12 and 13. Both clusters were followed by a period of 4–5 days when no waves were observed. This period of no waves continued during the declining phase of the fort-nightly envelope, and then the cycle was repeated. The largest amplitude waves in each cluster were 24 h apart, with a smaller amplitude wave in between. The smaller wave did not evenly split the time interval by hours but rather varied from wave-to-wave. The amplitude of the waves in cluster 2 was
Fig. 3. De-meaned bottom pressure (red line) and high-pass filtered temperature fluctuations at 140 m (blue line) at site S7 on the 350 m isobath during the ASIAEX experiment. The blue “spikes” indicate thermocline depressions due to passing solitons. Note the time of soliton occurrence with respect to the local barotropic tide, as described in the text.
TABLE II
BAROTROPICTIDAL CONSTITUENTSFROM THESEAGAUGESBE26 TEMPERATURE/PRESSURERECORDER
DEPLOYED ATASIAEX SITES7. THETIDESWEREMIXED, DIURNALDOMINANT, ASSHOWN INFig. 3
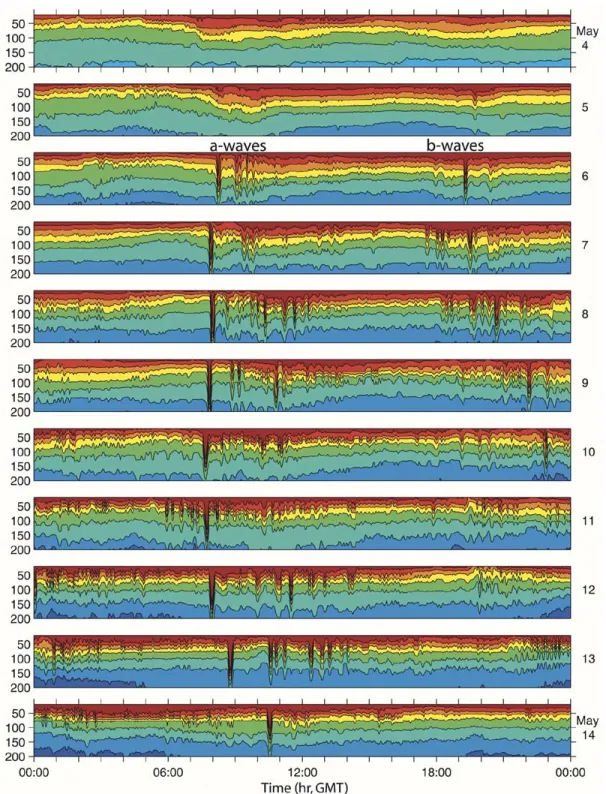
clearly greater collectively than cluster 1. The cluster 2 waves caused thermal displacements about 3 C greater than cluster 1, which translates to more than 50 m of amplitude given the ambient stratification. The explanation for this is complex and somewhat speculative and is left to the discussion section. The packet structure and timing of the wave arrivals over the continental slope can be seen in greater detail using daily stack plots of the temperature at mooring S7 (Fig. 4). This figure shows all the wave arrivals from cluster 2 (May 4–14), starting a few days before they commenced and continuing through the last of the large wave packets. For clarity, only the upper 250 m is shown, although in some cases (May 8–9) the waves extended beyond this depth. The properties of the cluster 1 waves (April 21–May 1) were similar except where noted.
Starting from the top of the plot, there were no high-frequency waves visible on May 4 and 5, although a strong semidiurnal tidal bore was clearly evident. The earlier bore had larger am-plitude than the second one later in the day. The beginnings of a very small soliton were starting to show up on the second bore around 1900 on May 5. On May 6, the first large waves arrived in earnest. There were two packets per day, which shall henceforth be referred to as the “a” waves for the earlier packet and the “b” waves for the later one. The a-waves were stronger by far than the b-waves and quite different in character. For the a-waves the largest soliton was always in the lead with smaller peaks be-hind, sometimes rank-ordered and sometimes not. The b-waves usually consisted of only one large peak which grew out of the center of a packet rather than at the leading edge. The a-waves
Fig. 4. Stack plot of temperature at mooring S7 on the 350 m isobath. The bottom 150 m are not shown to allow a clearer presentation of the internal wave structure. All available temperature sensors (Fig. 2, Table I) were used to construct the plot. Each panel is one day (May 4–14, 2001) from 0000 to 2400 h.
were associated with the stronger of the two tidal bores, and the b-waves with the weaker bore.
The a-waves arrived diurnally with remarkable regularity, arriving about 0800 GMT every day. From May 6–9, the high-frequency wave amplitude increased and the amplitude of the associated tidal bore decreased, consistent with an increasing energy transfer from low-to-high frequencies [2]. The elapsed time between the first and second solitons in each packet also increased during this period (Table III) suggesting increasing wave dispersion with increasing amplitude. On May
11, five smaller waves appeared ahead of the main soliton. The velocity field (see propagation section) shows that these waves came from a different source and were interfering with the main wave packet. On May 13 and 14, the lead soliton arrived at S7 progressively later by 1 hour on May 13 and an additional 1.5 hour on May 14. This phenomenon was not observed in the cluster 1 waves and may be due to the passage of a tropical cyclone across the wave propagation path (see discussion section). The number of a-waves per packet varied from day to day but ranged from 3 to 9 (Table III).
TABLE III
A SUMMARY OF THEOBSERVED ANDCALCULATEDWAVEPROPERTIES FORINTERNALSOLITARYWAVEPACKETSOBSERVEDDURINGASIAEX 2001. THE
MAXIMUMAMPLITUDEWASCALCULATEDUSING THEDISPLACEMENT OF THE24 C ISOTHERM.THEWAVELENGTHIS THEDISTANCEBETWEEN THELEADING
TWOTHERMOCLINEDEPRESSIONS IN THEPACKET, ESTIMATED BYCONVERTINGTIME TODISTANCEVIA THEOBSERVEDPROPAGATIONSPEED. WHEREMULTIPLE
VALUESAPPEAR, THEYARE THEDISTANCEBETWEEN THEFIRST ANDSECOND, SECOND ANDTHIRDPEAKS,ANDSO ON. THEHALF-WIDTHWASLIKEWISE
ESTIMATED BYCONVERTINGTIME TOSPACEVIA THEWAVEPROPAGATIONSPEED
The first of the b-waves arrived at around 1900 on May 6, 11 hours after the lead a-wave of the same day. The b-wave amplitudes, including the largest peak, were uniformly smaller than the a-waves (Table III). Unlike the a-waves, the b-waves arrived about an hour later each day, approximately like the M2 tidal progression. (Note that the b-waves wrap around from the end to the beginning of the plot on May 12). By the end of the record, the a-waves nearly merged with the lagging b-waves from the cycle before, but then a period of no waves began and this never actually happened. Interfering waves must therefore arrive from a different source.
Several unusual features of this plot might be explained by the structure of the tides in the generation region. The data suggest a diurnal inequality in the tides at the generation site, with the a-waves generated on the stronger of the two semidiurnal pulses. The a-waves also seem phase-locked to the nonprogressing di-urnal tide while the b-waves were in tune with the semididi-urnal tide. This may also be a feature of the generating tide. The re-markable regularity with which the waves arrived suggests they were riding on the tidal bore over most of the propagation path. The waves might thus correctly be referred to as solibores [42]. This issue is examined in greater detail in subsequent sections of the paper.
C. Wave Transformation in Shallow Water
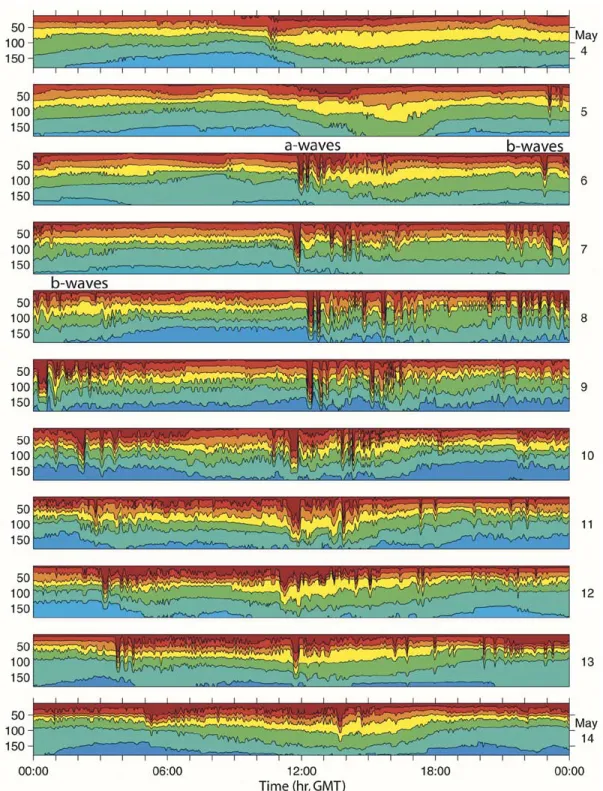
At mooring S5 (Fig. 5) the a-waves began arriving around noon and the b-waves at 1900. Tidal bores were again evident
not only on May 4–6, but again during May 10–14. Since this second bore was diurnal and was not observed at mooring S7, it was likely generated locally over the continental slope between moorings S7 and S5. It did not appear until the local tide ap-proached the spring tide. In a companion paper, the local gener-ation of internal tidal bores has been analyzed in greater detail [2]. They found that the critical bottom slope for diurnal tide generation over the observed buoyancy frequencies varied be-tween 0.15–0.40, and that this range of slopes was found over a broad area of the bottom near mooring site S6. Thus, these results are consistent with the local generation of a diurnal in-ternal tide between moorings S7 and S5. These large amplitude internal oscillations at tidal frequencies were also evident in the ASIAEX SeaSoar data near moorings S5 and S4 [3].
Like at mooring S7, the solitons at S5 were all waves of de-pression causing very large increases in temperature at each depth. During May 6–9, the amplitudes of the lead solitons in the a-waves was smaller at S5 than at S7 due to the presence of the bottom at 200 m. On May 6, 8, and 9, the lead soliton in the a-wave packets had split into two smaller peaks at S5, possibly due to wave fission [32], [43]. There was a pronounced change in the a-waves between May 6–9 versus May 10–13. The later waves were smeared out by advection due to the local in-ternal tide and were much broader than the May 6–9 waves. The b-wave packets at S5 arrived about an hour later each day similar to the b-waves at mooring S7. The b-wave solitons also equili-brated in amplitude somewhat, but the central peak persisted for
Fig. 5. As in Fig. 4 but for mooring S5 on the 200 m isobath. The entire water column is shown.
some packets (May 10–12). No wave splitting was observed in the b-waves. This was likely because the wave amplitude was so much smaller to begin with in the b-waves than the a-waves that it was less impacted by the bottom at S5. By May 15, all the solitons at S5 had disappeared.
The wave field was radically altered by the time it reached site S4 on the 120 m isobath (Fig. 6). An important thing to notice in this plot is the appearance of elevation waves (indicated by the magenta underscores) which lifted bottom water up near the surface causing sudden drops, rather than elevations, in temper-ature at mid-depth. As described in the introduction, these
eleva-tion waves are expected when the upper layer thickness exceeds the lower layer thickness. Clearly this situation developed sev-eral times during the experiment at site S4. Multiple processes contributed to the formation of elevation waves, some of which are described below.
There were no waves at all arriving on May 4 and 5 as the b-wave from late in the day on May 5 at S5 did not arrive at S4 until early May 6. The pronounced tidal bore of May 4 and 5 propagated all the way up the shelf without spawning any new waves, apparently not quite strong enough to do so anywhere along its path. The stronger a-waves arrived at S4 at
Fig. 6. As in Fig. 4 but for mooring S4 on the 120 m isobath. The top 100 m are shown. The magenta underbars indicate regions where elevation waves have formed.
about 1400 on May 6–9 but took on a very different form with respect to mooring S5 (Fig. 5). The huge lead solitons at S7, which split into two waves at S5, formed broad thermocline de-pressions at S4. This is because the soliton peaks were pushed up by the shoaling bottom and became broader also, since the soliton width is inversely proportional to its vertical displace-ment. An explanation of the wave widening and deformation in terms of linear wave speed changes for a thermocline transition from near-surface to near-bottom depth can be found in the lit-erature [37], [44]. Essentially, the nonlinear processes no longer
counteract the varying linear wave speed computed throughout the wave to allow a wave of permanent form, and the trough and shoulders of the wave diverge as the bathymetry shoals. In the wake of this broad lead depression, many packets of eleva-tion waves developed. An outstanding example of this would be on May 7 between 1400 to 1700 h. The elevation waves were very narrow, closely spaced, and approximately equal in height. Some of the waves contained water which was anoma-lously cold. This water was likely lifted up from very near the bottom (below the deepest sensors).
During May 10–13, the internal tide created a period when the thermocline was very close to the bottom from roughly 0600 to 1800 h. During this time, packets of elevation waves formed both near the front and back of the bore, for example during 0600–0900 and 1400–1700 hours. During the high-side of the cycle from 1800 to 0600 the next day, depression solitons formed. This is easily explained via the well known theory that when the upper-layer depth is thinner than the lower-layer depth (the usual deep water case) depression waves form, but when the upper layer is thicker than the lower layer, elevation waves form. Mathematically this occurs when the nonlinear pa-rameter changes sign [7]. Clearly, the criterion for elevation waves was met during 0600–1800 hours when the thermocline was nearly on the bottom. At other times the thermocline was slightly above mid-depth and the usual depression waves formed. An important point to emphasize is that the “critical location” where goes to zero is dynamic rather than static, and is not fixed to a particular isobath. The upper layer thick-ness is impacted by mesoscale variability, the internal tide, and indeed the internal waves themselves which sometimes cause broad regions of thermocline depression as they widen and run together. Elevation waves can then develop out of these regions. Mooring S3 was located on the 80 m isobath 18 km shore-ward of S4 on the continental shelf. This mooring was lost to fishing activity during the second half of the ASIAEX experi-ment, and thus plots similar to Figs. 4–6 are not available. By studying the S3 data for the cluster 1 waves (not shown) how-ever we can say that the waves were highly attenuated by the time they reached S3. The waves there were a mixture of eleva-tion solitons and oscillaeleva-tions which resembled ordinary linear internal waves. The WHOI Low-Cost (LOCO) moorings were set in the region between S4–S2 and provide a more detailed look at wave evolution in this region. This is one subject of an-other manuscript in this volume [2].
D. Wave Propagation
The uniqueness of each wave packet was an asset in terms of tracking its propagation from one mooring to the next through the array. Even so, not all packets could be accurately tracked, since they changed too much between moorings. Moorings S7, S6, and S5 were used for this exercise since the bottom interac-tion effects were not too severe. Mooring S6 was a velocity-only mooring and is thus not shown in the temperature time series (Figs. 4–6) but was used in tracking the velocity peaks. The elapsed time between moorings was easily determined from the time series (compare for instance a-wave arrivals in Figs. 4 and 5), however to compute the phase speed the geometry of the moored array and the direction the waves were propagating to-ward must also be accounted for. The waves were not propa-gating with crests normal to the moored array line but rather at some angle with respect to it. This angle was determined for each wave using the orbital velocities from the time series and SAR images when available [45].
The inferred propagation speeds from peak tracking showed a range of speeds from 0.83 to 1.84 m s with a mean of about
Fig. 7. Observed phase speed of the ASIAEX internal solitons computed by tracking the wave packet velocity structure between moorings S7 and S5 (circles), S6 to S5 (triangles), and S7 to S6 (squares). The a-waves are plotted in the top panels and the b-waves at the bottom, both against the same time axis. The observed wave amplitude (m) at mooring S7 is given by the number above each day. The methodology is described in detail in the text.
1.25 m s (Fig. 7, Table III). The consistency between moor-ings in Fig. 7 was good, indicating that bottom interaction did not alter the wave speed very much in this depth range. How-ever, there was no correlation at all between the nonlinear wave amplitude (indicated by the number above each column) and the phase speed. This again indicates that all the waves were being advected by the internal tide. The cluster a- and b-waves both showed a slight increase in phase speed with time. This was perhaps due to increasing stratification in the SCS basin during April and May, although there is little data to support this notion. Both sets of type a-waves displayed a minimum in the phase velocity in the middle of the cluster, while the phase speed decreased across each b-wave cluster. These small devi-ations from the mean phase speed were weakly correlated with nonlinear wave amplitude for clusters 1-a and 2-b, but were not correlated with wave amplitude at all for clusters 2-a and 1-b. The reason for these deviations is thus not obvious but may be due to some nuance in the fortnightly tidal cycle at the genera-tion site.
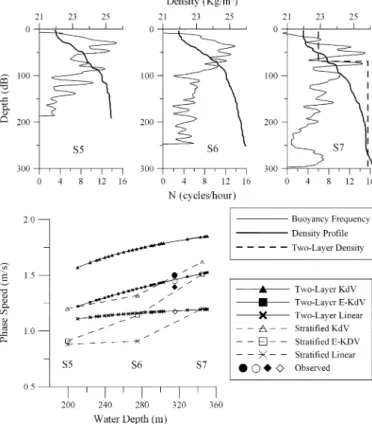
The phase speeds were also computed theoretically using the two-layer and continuously stratified KdV and EKdV formula-tions. The density stratification and buoyancy frequency profiles used in the calculations were obtained via a CTD cast at each mooring site [Fig. 8 (top)]. For the two-layer studies, a fit to the
Fig. 8. Observed and theoretical phase speed for the nonlinear internal waves observed in the ASIAEX region. The theoretical curves are identified as in the legend, calculated using the mean density and Brunt–Vaisala frequencies plotted at the top. The observed symbols are the averaged values from Fig. 7. From bottom to top, the symbols represent the mean phase speeds for cluster 1-a (open diamond), cluster 1-b (solid diamond), cluster 2-a (open circle) and cluster 2-b (solid circle).
350 m profile was used as the deeper data there were most repre-sentative of the stratification along the entire wave propagation path.
The wave amplitude (or “displacement”) is a necessary input for all the theoretical calculations. Traditionally, this has been computed in the literature as
(1) where is computed using the high-passed (IW) time series and the vertical gradient using some form of smoothed series similar to the ASIAEX low-passed time series. This method failed for the ASIAEX data, however, because the waves were so large that the surface water was depressed down past many of the sensors. Once this happened, the fluctu-ation looked the same for all the waves and did not represent an accurate measure of the wave amplitude. Alternatively, the wave amplitude was computed as the displacement of the 24 C isotherm as each soliton passed by mooring S7. This was made possible by the close thermometer spacing. The undisturbed depth of this isotherm was about 50–60 m in the lower ther-mocline and it did not surface during the experiment. This measure is likely an underestimate of the true wave amplitude but provides a good measure of the relative amplitude of the arriving waves. For example, the amplitude in the May 8 wave was 138 m using the displacement of the 24 C isotherm but exceeded 200 m at 140 m depth using (1). For the phase speed
calculations, the relative speed of the waves was of interest, so the amplitudes from the displacement of the 24 C isotherm were used.
The results (Table III; Fig. 8 (bottom)) show the difficulty of simulating these very large amplitude nonlinear waves using the conventional approaches. The two-layer KdV theory produced phase speeds that were too high and half-widths that were too small by a factor of two. The two-layer EKdV theory returned much better agreement with the observations for both the width and phase speed for waves of moderate amplitude, but broke down completely for the very large waves (greater than 88 m). Some overlap in the observed vs. calculated phase speeds is ev-ident, however it seems fair to say that collectively, the EKdV theory provided a better estimate of both the soliton widths and phase speeds than the KdV (Table III; Fig. 8). A new theoretical approach is needed for the very large waves. The error in the data is too great to discern between the two-layer and continuously stratified EKdV case, likely due to the very sharp thermocline which closely approximated a two-layer system at 350 m depth and deeper. The theory indicates that the waves were already starting to slow down between S7 and S5 although this was not obvious observationally (Fig. 7). Their propagation speed across the South China Sea’s northeast deep basin was likely closest to the speed at mooring S7, where both the EKdV models and the observations indicated a mean phase speed of about 1.5 m s . This value will be used subsequently in the discussion section to estimate the propagation time from the generation site.
E. The Generation Site
A well known property of the highly nonlinear internal soli-tary waves is that they propagate in the direction of the upper layer velocity [7]. The waves make a very obvious signal in the high-passed data with the velocity maximum typically a factor of ten or more above the background noise. These characteris-tics were exploited to set up an automated procedure to study the strength of the waves and their direction of propagation, and using reverse ray tracing, to determine their most likely point of origin. For this exercise, the data from mooring IW1
de-ployed at 21 during April 2000 was added to
the mix, since it was closer to Dongsha Island and also contained many soliton packets. The analysis depth was chosen for good signal to noise ratio and was 100 m for IW1, 97 m for S7, and 60 m for S6, S5, and S4. For each mooring, the vector speed and direction were computed above some threshold value de-signed to include only the solitons and exclude the background noise. The high-passed filtered data were used for the screening process and the unfiltered data were used in the calculation, that is, advection by the large-scale flow was included. Histograms of speed and direction were then constructed using all the data meeting the prescribed criteria (Fig. 9). These histograms are very revealing and provide statistical explanations for many fea-tures seen in the data.
A threshold of cm s for the u-component at S7 and IW1 excluded all but the largest solitons [Fig. 9(a)]. The S7 data had a single peak toward 282 true north , which points directly at the Batan Islands in the Luzon Strait. Thus, all the largest solitons originated from near these islands. The speed histogram shows that the very large waves were somewhat
Fig. 9(a)–(d). Histograms of current speed and direction for all solitons having greater than a certain threshold speed in the east-west (u) velocity component. The u-component was used to screen the data however the values on the x-axis denote the total vector velocity in the wave. The number of waves having that velocity is indicated by the length of the bars. The number of occurrences in the polar direction histograms is indicated by the dotted circles labeled in italics. From top to bottom, the four panels are for: (a)S7; 97 m; u > 50 cm s ; (b)IW1; 100 m; u > 50 cm s ; (c) S7; 97 m; u > 25 cm s ; and (d)IW1; 100 m; u > 25 cm s .
anomalous: Waves with speeds below 100 cm s were much more common than waves with speeds over 100 cm s . At IW1, there were many more solitons spread over a range of speeds, with a strong direction peak again appearing at 282 T. At this site however there were also some waves heading toward the northeast. To try and quantify this further, threshold was lowered to 25 cm s which included many more waves [Fig. 9(c) and (d)]. This revealed more waves at S7 propagating in other directions, and a clearly bimodal direction histogram at IW1 with peaks at 282 T and 55 T. The waves in this second peak were coming from the southwest (235 T), which points directly to Dongsha Island. Thus, all the largest waves observed at S7 and IW1 were coming from the Luzon Strait, while many of the smaller waves were coming from around Dongsha.
Fig. 9(e)–(h). As in Fig. 7(a)–(d), except for different moorings, depths, and threshold velocities. From top to bottom, the four panels are for: (e) S6; 60 m; u > 50 cm s ; (f) S6; 60 m; u > 20 cm s ; (g)S5; 60 m; u > 20 cm s ; and (h)S4; 60 m; u > 20 cm s . Lower thresholds had to be used in shallower water as the soliton amplitude decreased.
This result is visually supported by the synthetic aperture radar (SAR) imagery (Fig. 10) which clearly shows this island refraction phenomenon. Referring back for a moment to Fig. 4, the waves leading the largest soliton on May 11 were in fact among those propagating toward 55 T, and were thus coming from around Dongsha Island and were not part of the May 11 trans-basin packet.
The wave histograms from shallower water [Fig. 9(e)–(h)] provide clues to what is happening there. At S6, the large waves were still heading WNW but slightly more toward the north toward 292 T. This difference is ascribed to refraction by the shoaling bottom and can also be observed in the curvature of the wave fronts as seen in Fig. 10 and other SAR images [45]. A single large wave at S6 appears to have been reflected. Moving into still shallower water, the waves fill up the left hemisphere of the direction histograms bounded by a line between 150 to 330 T, approximately normal to the continental shelf break. This is due to a combination of reflection, refraction, and
Fig. 10. Synthetic aperture radar (SAR) image from May 18, 2001 showing incident and refracted waves around Dongsha Island near the ASIAEX region. The moorings IW1 from April 2000 and S7 from April–May 2001 are also indicated.
alongshore advection by the mean flow, which was toward the southwest at all times. Based on these results, it is easy to see how the wave packet structure quickly becomes very complicated in the vicinity of the shelf break.
F. Modal Structure of Wave Packets
While each wave packet was unique with respect to the number, spacing, and amplitude of the solitons it contained, certain features of the waves were robust from packet-to-packet and are described here using two examples, one for depression waves at S7 [Fig. 11(a)] and the other for elevation waves at S4 [Fig. 11(b)]. There were four clear solitons in the May 8 packet [Fig. 11(a)] before the background noise level was reached. The solitons in this packet were approximately rank-ordered, i.e., decreasing in amplitude and period from front to back. About 2.3 h elapsed between the first and second peaks, 1.0 h between the second and third, and 0.5 h between the third and fourth. The large elapsed time between the first two waves was typical of all the a-waves and indicates significant dispersion, suggesting the waves traveled a great distance. This time is much greater than that of previously observed waves on conti-nental shelves where it is typically only 15–20 min for waves generated close by [24], [46]. For the Sulu Sea it was typically about 40–50 min for waves that had been traveling for two days across the sea [26]. The waves left a small but discernable trailing thermocline depression in their wake, also consistent with previous observations and theory [32], [33].
The zonal and vertical velocity components [Fig. 11(a)] show the strength, direction of propagation, and modal structure of the waves. For clarity, only the u-component is shown since it contained most of the velocity and the v-component exhib-ited similar vertical structure. These were classic mode-1 waves, with opposing velocities in the upper and lower layers and a node somewhere between 90–150 m depth, apparently closer to 150 m given the weaker currents there. For the leading, largest-amplitude wave, the (u, v) velocities in the upper layer were cm s respectively indicating propagation toward 307 true north (WNW). The opposing lower-layer velocities (u, v) were weaker at cm s and spread over a broader depth range than the upper layer velocities. There was a sharp negative (downward) vertical velocity ( cm s ) just ahead of the thermocline depression and a positive (upward) vertical velocity (40 cm s ) behind it. In between, over the width of the pulse, there was a slower upward velocity of about 10–15 cm s . The maximum horizontal velocities were also observed during this time, between the two vertical pulses. This velocity structure agrees well with the theoretical expectation for internal solitary waves [7], and was consistent among the leading waves in the other packets as well. The third and fourth peaks arriving at 1115 z and 1145 z were actually moving in a slightly different direction rotated 40 toward the north. This can likely be explained by the stronger curvature of the trailing wave fronts as seen in the SAR imagery [45].
At S4, the depression soliton from offshore was still visible as a broad, leading, thermocline depression from 1400 to 1430 h. The horizontal velocity components were consistent with those
Fig. 11. (a) Temperature and vertical velocity (top panel), and u-component (bottom panel) for the May 8 soliton packet observed at ASIAEX mooring S7 on the 350 m isobath. The vertical velocity (white line, top) was sampled by the 90-m ADCP range cell, one of the closest bins to the transducer heads. The upper layer horizontal velocities are from the ADCP and the lower layer velocities are from the three Aanderaa current meters.
described above but this broad depression had no signature at all in the vertical velocity. This depression was likely created off-shore of S4, or perhaps sub-observation scale turbulence occur-ring in this region smeared out the vertical velocity [4]. Trailing the downward pulse, a packet of seven elevation waves appeared [Fig. 11(b)]. These waves looked nearly uniform in amplitude but were rank-ordered in velocity. Each elevation soliton was preceded by a strong upward pulse of vertical velocity followed by a trailing downward pulse. The magnitudes were still quite strong, about 30 cm s upward on the leading edge and 25 cm s downward on the trailing edge. The horizontal velocities were order 50 cm s offshelf in the upper layer and 35 cm s onshelf in the lower layer. The nodal point can be better iden-tified using the ADCP data at S4 than with the broadly spaced
current meter data at S7 and occurred at around 66 m depth. The polarity of the waves was reversed with respect to the depression waves observed further offshore. This description of the orbital velocities for elevation waves is once again in excellent agree-ment with previous theoretical work [7].
IV. DISCUSSION A. Soliton Generation vs. Luzon Strait Tides
The temperature and pressure time series at Mooring S7 indicated an unusual relationship between the appearance of the waves and the fortnightly beat of the local barotropic tides (Fig. 3). It has now been demonstrated however that the largest waves were generated in the vicinity of the Batan
Fig. 11. (Continued.) (b) Temperature and ADCP vertical velocity (top panel), and u-component (bottom panel) for the May 7 soliton packet observed at ASIAEX mooring S4 on the 120 m isobath. The vertical velocity (white line, top) was sampled by the 60-m ADCP range cell, near the maximum displacement in the waves. In the lower panel, the velocities are from 42 m (red), 70 m (green), and 98 m (blue) respectively.
Islands in the Luzon Strait, some 485 km away. Given the paths and estimated propagation speed (1.5 m s ) presented above (Fig. 8, Table III) it would take the waves about 3.7 d to travel from the generation region to the observation point. Based on scatter in the phase speed observations and variation in the total path length traveled, the error in this calculation is around 0.25 m s , which translates to about a half a day over the distance traveled. Therefore, the relevant comparison is the phase relationship between the Luzon Strait tides and the time the waves arrived at the ASIAEX array lagged back by
approximately days.
Since no in situ observations were made in the Luzon Strait as part of the ASIAEX program, the tides there were calcu-lated using the global tidal model PCTides [47]. PCTides is an easily relocatable, 2-D (barotropic), depth integrated, constant density, data assimilative model which has been rigorously ver-ified at several sites around the world. All the major data bases
needed to run a simulation including DBDB5 topography are imbedded in the model. The tidal phases and heights on the open boundaries are taken from the Grenoble FES95.1.2 stan-dard. The model computes the M2, S2, K2, N2, O1, K1, Q1, and 2N2 tidal components. This is not a complete picture by any means, however these eight components contained 78 per-cent of the observed variance in the pressure gauge deployed at station S7 (Table II).
For this application, the boundaries of the region to be simu-lated (15–26 N, 115–125 E) were chosen to be in open water well away from both the ASIAEX observations and the Luzon Strait. Other boundaries were tried and the model results were not sensitive to this. There were 54 tidal stations within this re-gion which were included in the simulation, i.e., the model was well constrained. As a check, the tidal heights were first com-puted at mooring S7 for comparison with the moored pressure gauge there and the agreement was excellent [Fig. 12 (bottom)].
Fig. 12. Bottom: Observed (green line) and PCTides-generated (red line) barotropic tidal amplitudes at ASIAEX site S7 on the Chinese continental slope. Middle: The barotropic tidal height at Batan Island in the Luzon Strait, as computed by the global tidal model PCTides. Top: The high-pass filtered temperature fluctuations at 140 m (blue line) at ASIAEX site S7 on the 350 m isobath, phase-shifted 3.7 days to the left (earlier) to account for the propagation time between the proposed generation site (the Luzon Strait) and the mooring.
The model overestimated the tidal heights with an rms differ-ence of 15 cm, but the mixed diurnal-dominant nature of the tide and the fortnightly beat were accurately reproduced. As a fur-ther check, the PCTides output for 20 (between Batan and Sabtang Islands) was compared against the Oregon State University (OSU) TOPEX/Poseidon crossover global in-verse solution TPXO.3 [48] for the same location. TPXO.3 is a different global model of ocean tides, which best-fits, in a least-squares sense, the Laplace Tidal Equations and crossover data from the first 40 TOPEX/Poseidon orbit cycles. The inputs and methodology are quite different from the PCTides model, however the two models produced virtually identical results for the locations studied in the northeastern SCS and Luzon Straits. These model/data and model/model comparisons provide rea-sonable confidence that the model-generated tidal heights in the Luzon Straits are correct.
The simulated tides between the Batan and Sabtang Islands in the Luzon Strait [Fig. 12 (middle)] were very different from the Chinese continental shelf. The Luzon tides remained semidi-urnal even at spring tide, and the fortnightly beat was shifted ear-lier by 3.5 days. This resulted from a net phase shift between the diurnal and semidiurnal tidal components of about 35 between the Luzon Strait and Chinese continental shelf. When the soli-tons, as indicated by the temperature fluctuations at S7 lagged back 3.7 days to allow for propagation, are plotted together with the PCTides-simulated Batan Island tides (Fig. 12), sev-eral interesting relationships become apparent. Given the error in the calculation, one cannot attribute individual waves to indi-vidual tidal peaks, but one can say: a) The solitons were gener-ated around the time of the spring tide and not during the neap tide, in agreement with many other locations around the world
[26]. b) The a-waves were generated on the higher-high tides and the b-waves on the lower high tides, which explains why the a-waves were both larger and more nonlinear. c) The ampli-tude of the a- and b-waves was most equal near the center of the clusters when the diurnal inequality at the generation site was minimal.
Armed with this new information from the global tidal models, we return to the issue of why the a-waves arrived daily at 0800 with such astounding regularity, while the b waves arrived about an hour later each day (Fig. 4). The cluster 1 waves (not shown) displayed similar behavior, but the cluster 1 a-waves arrived at around 1000 rather than 0800. There are two plausible explanations for this. The first is that the a-waves were phase-locked predominantly to the diurnal (K1) tide while the b-waves were associated with the M2 tide on the weaker of the two daily oscillations. With a period of 23 hours and 56 minutes, the K1 tide arrives at about the same time daily and the 4-minute changes would not be discernable within each cluster of waves, given all the other variability along the propagation path. Between the two clusters, the cluster 2 waves would arrive about an hour earlier than the cluster 1 waves a fortnight earlier. This shift has the correct sign but is not an exact match for the 2-h difference observed. The b-waves would arrive 50 min later each day as is usual for the M2 tide whose period is 12.42 h. This unusual tidal structure should be observable at the generation site but was not present in the output from the global tidal models (Fig. 12). It would likely result from local topographic interactions and it is not obvious that this could be reproduced by a global tidal model. This explanation remains just a hypothesis which could benefit from additional in situ observations at the generation site.
The second possibility is that both wave types advanced 50 min/day, but the lead soliton continued to arrive at about the same hour of the day during May 6–9 because its phase speed was increasing along with its amplitude and nonlinearity. Restated, the lead soliton out-ran the pack by a little more each day by an amount proportional to its increasing amplitude. This would also manifest itself as increased dispersion, with increasing elapsed time between the arrival of the first two peaks in each packet. This was in fact observed during May 5–9 (Fig. 4, Table III) but on May 10–11, the wave amplitude decreased by 60 m and the lead soliton did not fall behind, still arriving at 0800 daily. A more quantitative analysis also proved inconsistent with this explanation. To travel the 485 km dis-tance between Luzon and S7 one hour faster each day requires only a 2-cm s speed increase with respect to the day before. The lead soliton increased in amplitude by about 20 m per day during the May 5–9 time period. Under the fully stratified deep water EKdV theory, an amplitude increase of 20 m in open water provides an increase of order 19 cm s in the nonlinear phase speed, which would cause the waves to arrive 10 hours earlier each day. Clearly this was not observed, and in fact very little correlation was observed between wave amplitude and phase velocity at all (Fig. 7, Table III). Given these results, the more likely explanation seems to be that the wave arrivals were somehow linked to the diurnal (a-waves) and semidiurnal (b-waves) tides in the generation region, although the physical mechanism for this is not clear. Some direct current observa-tions from the Luzon Ridge in the vicinity of the Batan Islands would be useful in sorting this out.
B. Wave Amplitudes in Cluster 1 Versus Cluster 2
One of the most obvious and robust features of the data set (Fig. 3, Table III) is that the amplitude of the cluster 2 waves was much greater than the cluster 1 waves, in both displace-ment and velocity, by any measure you might choose. Why should this be? The strength of the waves arriving at S7 de-pends on both the conditions at the generation site and con-ditions encountered along the route as the waves propagated 485 km across the northeastern South China Sea. Considering first wave generation, the initial strength of the waves depends on the total flow across the sill and the local stratification at the sill. Both these parameters depend not only on the tides, but also the mesoscale variability, in this case the position of the Kuroshio intrusions into the Luzon Strait. According to the global tidal models (Fig. 12) the Luzon Strait barotropic tide varied little between the two wave clusters, so the state of the Kuroshio inflow was the more likely cause of the amplitude vari-ability between clusters.
As reviewed in the introduction, the Kuroshio sometimes swings through the SCS and sometimes not. The main current sometimes passes over the shallow portion of the Luzon Ridge (which includes the Batan Islands), and sometimes loops around it, entering and exiting the sea via deeper water to the south and north of the islands. Assuming the wave generation mechanism is similar to other locations such as the Sulu Sea, the Straits of Gibralter, and Massachusetts Bay, the initial hydraulic jump which generates the waves forms on the ebb (southeastward) tide. The waves are then released on the flood (northwestward)
Fig. 13. Bottom topography (colors) and current vectors at 100 m depth (white arrows) as computed by the NRL North Pacific Nowcast/Forecast system (NPACNFS) showing the difference in the flow through the Batan Islands on April 21 (top, internal wave cluster 1) versus May 11 (bottom, internal wave cluster 2). The ASIAEX internal waves are presumed generated around the island group centered near 20 20’N, 122 00’E in the Luzon Strait. The stronger NW flow on April 21 weakens the total flow across the sills at ebb tide, causing weaker solitons to be generated. (Figure courtesy of Dr. Dong-Shan Ko, Naval Research Laboratory).
tide and propagate WNW across the sea. Under this scenario, Kuroshio positions that enhance the ebb tide would contribute to stronger internal bores and subsequently, solitons while Kuroshio flows that oppose the ebb tide would lead to weaker solitons.
Lacking in situ observations in the Luzon Strait, the position of the Kuroshio can be estimated instead using the output from the NRL North Pacific Nowcast/Forecast System (NPACNFS). The currents at 100 m were compared for the April 21, 2001 (cluster 1) and May 11, 2001 (cluster 2) time frames (Fig. 13). During this time, the model indicates that the Kuroshio was in the process of intruding further westward into the South China Sea. On April 21, there was a slight intrusion leading to a strong