設計高效能的通用型粒子群最佳化演算法

國

立

交

通

大

學

資訊學院 資訊學程

碩

士

論

文

設計高效能的通用型粒子群最佳化演算法

Designing an Efficient General-purpose Particle Swarm

Optimization Algorithm

研 究 生：陳卓平

指導教授：陳 稔 教授

何信瑩 教授

設計高效能的通用型粒子群最佳化演算法

Designing an Efficient General-purpose Particle Swarm

Optimization Algorithm

研 究 生：陳卓平 Student：Cho-Ping Chen

指導教授：陳 稔 Advisor：Zen Chen

何信瑩 Shinn-Ying Ho

國 立 交 通 大 學

資訊學院 資訊學程

碩 士 論 文

A Thesis

Submitted to College of Computer Science National Chiao Tung University in partial Fulfillment of the Requirements

for the Degree of Master of Science

in

Computer Science July 2007

Hsinchu, Taiwan, Republic of China

設計高效能的通用型粒子群最佳化演算法

學生：陳卓平

指導教授：陳 稔

何信瑩

國 立 交 通 大 學

資 訊 學 院 資 訊 學 程 碩 士 班

摘

要

解最佳化問題為許多研究領域的重要課題，演化式計算為解最佳化問題的有效方法 之一，而粒子群最佳化又為新近發展的一種演化式計算演算法。一般而言，使用專家經 驗而為問題特別設計的演算法較能更有效率地解決特定的最佳化問題。然而，欲解最佳 化問題的研究學者大部份具有該問題領域的知識，但欠缺發展演算法的經驗能力。本研 究試圖發展一個通用型的粒子群最佳化演算法GPPSO 來解決各類型的最佳化問題。 GPPSO 使用了三個技巧來克服一些難題，如函數之參數間較強交互作用，具有眾多局 部最佳解的函數及具大量最佳化參數的函數：1)以均勻取樣來建立初始的粒子族群，2) 使用局部搜尋運算子的輔助，3)利用智慧型的粒子移動機制。GPPSO 的高效能主要是源 於使用直交實驗設計，藉由直交表和因素分析，能有效增加廣度和深度的搜尋效能；均 勻取樣的初始粒子族群能增加求解的穩定性。本論文針對GPPSO 的主要參數加以分 析，提供預設值，亦可加以調整。本論文使用文獻提供的標準測試函數庫，實驗結果顯 示GPPSO 與現有粒子群最佳化方法比較，其效能良好，可以作為解最佳化問題的通用 型演算法。 關鍵字：最佳化、粒子群演算法、智慧型粒子移動機制、直交實驗設計

Designing an Efficient General-purpose Particle Swarm Optimization

Algorithm

student：Cho-Ping

Chen

Advisor：Dr. Zen Chen

Dr. Shinn-Ying H

o

Degree Program of Computer Science

National Chiao Tung University

ABSTRACT

Solving optimization problems is an important issue in many research domains.

Evolutionary computation is one efficient method to solve optimization problems and particle swarm optimization (PSO) is a newly-developed algorithm of evolutionary computation. Generally speaking, the customized algorithm using expert experience can more efficiently solve specific optimization problems. However, the most researchers of solving optimization problems often have knowledge of application domains but not ability of developing the algorithm. This study aims to develop an efficient general-purpose particle swarm

optimization (GPPSO) algorithm to solve various kinds of optimization problems. GPPSO utilizes three techniques to cope with the difficulties of intractable functions such as strong interactions among parameters, multi-modal function and large number of parameters: a) initial particle swarm of uniform sampling, b) Solis and Wets local search and c) intelligent move mechanism. The high performance of GPPSO arises mainly from an orthogonal experimental design with orthogonal array and factor analysis which can effectively advance the search performance of exploration and exploit. Furthermore, the proposed initialization of particle swarm can advance robustness of obtained solutions. The main control parameters of GPPSO are analyzed and their default values of parameters are suggested or user-defined. This study utilizes some benchmarks to evaluate GPPSO by comparing existing particle

swarm optimization methods. The simulation results reveal that GPPSO performs well and can be served as an efficient general-purpose algorithm of solving optimization problems.

Keywords：Optimization, particle swarm optimization, intelligent move mechanism, orthogonal experimental design

誌

謝

在研究所的求學中，要感謝陳稔老師跟何信瑩老師，感謝老師的指導教誨，除了感 謝老師給我很多課業上的指導，包含研究的方向及研究的方法，更感謝老師對我的包 容。再來要感謝實驗室的學長姐跟學弟，他們給我很多的幫助，不管在軟體上、硬體上， 還有精神上的幫忙。最後要感謝我的家人給我的支持跟鼓勵。

目

錄

摘 要 ...i ABSTRACT ...ii 誌 謝 ...iv 目 錄 ...v 表 目 錄 ...vii 圖 目 錄 ...viii 一、緒論...1 1.1 研究背景與動機 ...1 1.2 研究目的 ...2 1.3 論文架構 ...2 二、相關研究...4 2.1 粒子群最佳化演算法 ...4 2.2 直交實驗設計 ...6 2.2.1 直交表 ...6 2.2.2 兩水準直交表的產生方式 ...7 2.2.3 多水準直交表產生方式 ...8 2.2.4 因素分析 ...9 2.2.5 直交實驗 ...10 2.3 Local Search ...10 2.4 智慧型粒子移動機制步驟 ...10

2.5 Dynamic Multi-Swarm Particle Swarm Optimizer with Local Search 介紹 ... 11

2.6 Orthogonal Particle Swarm Optimization(OPSO)介紹 ...12

2.7 基因演算法與 GPPSO 比較...12 2.7.1 基因演算法簡介 ...12 2.7.2 傳統基因演算法與粒子群演算法的操作對應 ...14 2.7.3 傳統基因演算法與粒子群演算法的相異之處 ...15 三、提出GPPSO 方法論...16 3.1 想法起源 ...16 3.2 理論基礎 ...16 3.3 GPPSO 之設計...18 3.3.1 GPPSO 流程...18 3.3.2 由直交實驗求出 GPPSO 參數...19 3.3.3 GPPSO 的方法全貌敘述...20 3.3.3.1 直交表初始化 ...20 3.3.3.2 Local search...20 3.3.3.3 智慧型粒子移動機制 ...21

3.4 GPPSO 與基因演算法的操作對應...21 四、實驗結果與效能分析...23 4.1 測試函數介紹 ...23 4.2 實驗說明 ...26 4.3 實驗設計 ...27 4.3.1 PSO 的預設參數...27 4.3.2 GPPSO 中個機制的實驗結果...33 4.3.2.1 單純的 PSO，與加入均勻取樣初始化的 PSO 的實驗結果比較 ...33

4.3.2.2 單純的 PSO，與加入 local search 的 PSO 的實驗結果比較 ...34

4.3.2.3 單純的 PSO，與加入 modified IMM 的 PSO 的實驗結果比較...34

4.3.3 CEC 2005 special session dimension 10 及 dimension 30 實驗結果 ...35

4.3.4 GPPSO 與 Dynamic Multi-Swarm Particle Swarm Optimizer with Local Search 的比較 ...42 4.3.5 GPPSO 與其他演算法比較...43 4.3.6 GPPSO 與 OPSO 的比較 ...45 4.3.7 GPPSO 演算法複雜度...45 4.3.8 GPPSO 中個機制的收斂速度比較...48 五、結論...57 5.1 結論 ...57 5.2 未來展望 ...57 參考文獻...58 附錄一...60

表 目 錄

表 2.1 兩水準三因素完全實驗 ...6 表 2.2 兩水準三因素直交實驗表 ...7 表 4.1 測試函數列表 ...25 表 4.2 直交實驗的參數表 ...27 表 4.3 4 9(3 ) L 的直交表...28 表 4.4 Dimension = 10，依據直交表產生的統計結果 ...28 表 4.5 Dimension = 10，因素分析 ...28 表 4.6 Dimension = 30，依據直交表產生的統計結果 ...29 表 4.7 Dimension = 30，因素分析 ...29 表 4.8 dimension = 10 直交表實驗數據(一)...29 表 4.9 dimension = 10 直交表實驗數據(二)...30 表 4.10 dimension = 30 直交表實驗數據(一)...31 表 4.11 dimension = 30 直交表實驗數據(二)...32 表 4.12 加入使用直交表求初始解的實驗數據 ...33 表 4.13 加入 local search 的實驗數據 ...34 表 4.14 加入 modified IMM 的實驗數據 ...34

表 4.15 Dimension = 10，result of Function 1-5...35

表 4.16 Dimension = 10，result of Function 6-10...36

表 4.17 Dimension = 10，result of Function 11-15...36

表 4.18 Dimension = 10，result of Function 16-20...37

表 4.19 Dimension = 10，result of Function 21-25...38

表 4.20 Dimension = 30，Result of Function 1-5 ...39

表 4.21 Dimension = 30，Result of Function 6-10 ...39

表 4.22 Dimension = 30，Result of Function 11-15 ...40

表 4.23 Dimension = 30，Result of Function 16-19 ...41

表 4.24 DMS-L-PSO 與 GPPSO 的實驗比較...42 表 4.25 25 個 test functions 之求解臨界值定義...44 表 4.26 GPPSO 與其他演算法比較解決的問題數...44 表 4.27 GPPSO 與 OPSO 的實驗數據比較 ...45 表 4.28 GPPSO 的演算法計算時間複雜度...46 表 4.29 DMS-L-PSO 的演算法計算時間複雜度 ...46

圖 目 錄

圖 2.1 兩水準三因素空間分佈圖 ...7 圖 2.2 基因演算法基本流程 ...13 圖 2.3 基本交配機制 ...14 圖 2.4 基本突變機制 ...14 圖 3.1 GPPSO 流程...19 圖 3.2 基因演算法突變機制與 IMM 對照...22 圖 4.1 演算法計算時間複雜度比較圖(一) ...47 圖 4.2 演算法計算時間複雜度比較圖(二) ...47 圖 4.3 函數 F 1 收斂比較圖...48 圖 4.4 函數 F 2 收斂比較圖...48 圖 4.5 函數 F 3 收斂比較圖...49 圖 4.6 函數 F 4 收斂比較圖...49 圖 4.7 函數 F 5 收斂比較圖...50 圖 4.8 函數 F 6 收斂比較圖...50 圖 4.9 函數 F 7 收斂比較圖...50 圖 4.10 函數 F 8 收斂比較圖...51 圖 4.11 函數 F 9 收斂比較圖 ...51 圖 4.12 函數 F 10 收斂比較圖...51 圖 4.13 函數 F 11 收斂比較圖 ...52 圖 4.14 函數 F 12 收斂比較圖...52 圖 4.15 函數 F 13 收斂比較圖...52 圖 4.16 函數 F 14 收斂比較圖...53 圖 4.17 函數 F 15 收斂比較圖...53 圖 4.18 函數 F 16 收斂比較圖...53 圖 4.19 函數 F 17 收斂比較圖...54 圖 4.20 函數 F 18 收斂比較圖...54 圖 4.21 函數 F 19 收斂比較圖...54 圖 4.22 函數 F 20 收斂比較圖...54 圖 4.23 函數 F 21 收斂比較圖...55 圖 4.24 函數 F 22 收斂比較圖...55 圖 4.25 函數 F 23 收斂比較圖...55 圖 4.26 函數 F 24 收斂比較圖...56 圖 4.27 函數 F 25 收斂比較圖...56

一、緒論

1.1 研究背景與動機

最佳化問題存在很多研究領域中，如生物資訊、自動控制、電路設計、資 料探勘、排程問題等，也廣泛存在於日常生活應用中，如行程規劃、資源分配等。 如何使用有限的資源，求出最佳的結果，為解決最佳化問題的基本概念。解決最 佳化問題也是研究發展進步的一大動力。 求解最佳化問題，使用最多的方式有，數值法(Numerical Method)、列舉法 (Enumerative)以及隨機搜尋法(Random Search)[1]。數值法是以局部(local)的觀點 在搜尋最佳解，因此並不能保證找到全域最佳解(Global Optima)，且當解空間不 平順或不連續的狀況下，數值法容易求到區域最佳解(Local Optima)。列舉法為搜 尋解空間裡所有的解，一定可以找到最佳解，但列舉法花費的成本過高，當解空 間很大時，此演算法所需的計算量相當驚人，演算法效率較低。鑒於上述兩種缺 點，隨機搜尋法受到重視且快速發展。演化式計算(Evolutionary Computation)基 礎概念為達爾文進化論[2]『適者生存，不適者淘汰(survival of the fittest)』的概念， 觀察及模擬自然界演化過程而建立的計算模式。粒子群最佳化演算法(Particle Swarm Optimization, PSO)為演化式演算法與隨機搜尋法的一種，由 James

Keenedy 和 Russell Eberhart 於 1995 提出[3][4]，粒子群演算法基本觀念為模擬鳥 群覓食過程，分享群體與個體間的訊息，使整個群體朝最有利的方向前進，達到 有效覓食的目標。 由於不同應用領域範疇的問題，通常無法使用一種通用型的演算法求解， 需依據不同問題的特性，需要加入考量問題的背景知識，選擇並適度修改演算 法，才能達到求解目的，所以選擇演算法時，需要對求解問題有相當程度的瞭解， 才能找出最適當的演算法，而開發一種實作簡單，可以適用於多種類型領域的演 算法，則是此篇論文的動機。

1.2 研究目的

本篇論文提出的演算法，期能達到適用各種類型的應用問題，包含可以解 決有較強交互作用的題目、有眾多局部最佳解及大量最佳化參數的問題，通用型 粒子群演算法加入三種機制，來達到可以解決多種類型的最佳化問題，其次，加 入考慮粒子群演算法使用到的參數，經由實驗結果，得到一組參數，此參數於多 種不同類型測試函數，有一定程度的搜尋效果。搜尋效果由測試評估函數求得的 精確值來判斷。 演算法的初始解產生方式是在解空間中隨機選擇初始搜尋點，當解空間複 雜且問題交互作用大時，這樣的隨機產生法效果不佳，為去除以隨機亂數產生的 不穩定性因素，初始解產生的方式，使用直交實驗設計推理出一組較佳的初始 解，增快演算法搜尋收斂速度。 粒子群演算法實作簡單，但缺點為容易落入區域最佳解，且在解空間大的 狀況，不容易找到最佳解，可以結合局部搜尋運算子(Local Search) [5]及智慧型 粒子移動機制(Intelligent Move Mechanism, IMM) [6]，解決上述問題。

粒子群演算法中使用的參數，如最大速度、慣性權重等，均會影響搜尋效 果，如何調整演算法參數設定，達到更好的搜尋結果，是很多研究的重點。本篇 論文中使用直交實驗設計(Orthogonal Experimental Design, OED)的推理能力與因 素分析(Factor Analysis)，找出一組通用的參數，可適用在不同的領域中，達到一 定程度的搜尋結果。

1.3 論文架構

本論文分為五個章節，其結構如下： 第一章，緒論，此章節包含研究動機與背景、研究目標及論文架構。 第二章，相關研究，相關研究中介紹粒子群演算法，以及通用型粒子群最佳化演 算法(General-purpose Particle Swarm Optimization, GPPSO)中使用到的相關機

制，包含直交實驗設計、智慧型粒子移動機制以及local search，並簡介參考比較 的其他演算法，包含Dynamic Multi-Swarm Particle Swarm Optimizer with Local Search(DMS-L-PSO)[7]和 Orthogonal Particle Swarm Optimization(OPSO)，章節最 後比較基因演算法與粒子群演算法的差異以及演算法中相關操作的對應關係。 第三章，描述通用型粒子群最佳化演算法(GPPSO)的流程，包含初始化步驟、local search 與智慧型粒子移動機制。

第四章，此章節內包含使用CEC 2005 special session 為測試函數的實驗數據、 GPPSO 與其他演算法的實驗數據比較。

二、相關研究

粒子群演算法為觀察物種現象，以模擬鳥群覓食的行為發展而來的演算法，其特點 為分享粒子與群體間的訊息，以達到群體最佳利益，當解空間大時，容易流於找到區域 最佳解，加入local search 與智慧型粒子移動機制，可以更有效率的找到最佳解。第二章 第一小節介紹粒子群演算法的基本概念，在第二小節描述直交實驗設計，其中包含直交 表的說明，以及直交表的產生方式，第三小節說明智慧型粒子移動機制，第四小節為local

search 的步驟，第五小節為 Dynamic Multi-Swarm Particle Swarm Optimizer with Local Search(DMS-L-PSO)介紹，第六小節 Orthogonal Particle Swarm Optimization(OPSO)介 紹，第七小節介紹基因演算法，以及基因演算法與粒子群演算法的操作對應。

2.1 粒子群最佳化演算法

粒子群演算法是演化式演算法，經由世代演化找出最佳解，其想法起源於 觀察鳥群覓食行為，透過分享個體與群體的訊息，使整個群體往最佳利益的方向 前進。 粒子群演算法以隨機方式產生粒子(particle)初始解，每一個粒子代表一個 個體，也表示位於解空間中的潛在解，每個粒子是在D 維度(dimension)搜尋空間 上的一個點，d = 1, 2, …, D，而多個粒子組成粒子群(swarm)，且 i = 1, 2, …, PS， PS 為粒子個數(population size)，粒子群演算法的相關定義如下： 第 i 個粒子定義為： 1 2 T max X ( , ,..., ) , 0,1, 2,..., D l l l l i = x xi i xi l= iter (2-1) 每一個粒子最好的位置可紀錄並定義為： T i 1 2 P =( ,pi pi ,...,piD) (2-2) 粒子群中最佳位置解的粒子定義為： T g 1 2 P =(p_g ,p_g ,...,p_gD) (2-3)

粒子位置改變的速率可定義為： T i 1 2 V =( ,v v_{i i} ,...,v_iD) (2-4) 初始的粒子位置定義為： Xl =1,2,...,PS, =0. i i l ， (2-5) 初始的粒子速度定義為： Vl =1,2,...,PS, =0. i i l ， (2-6) 粒子移動速度： l+1 l l l i i 1 i i 2 g i V = ×W V + ×c rand() (P -X )× + ×c Rand() (P -X )× ； (2-7) 且滿足_Vl 1 _V i + _≤ max限制 max min max max W W W W l iter − − × = (2-8) 粒子更新位置： 1 Xl Xl l i i i + _{= +V (2-9)} W 為慣性權重，影響全域搜尋與區域搜尋的平衡，慣性權重可以為一正數，或是 隨迭代數變化的線性或非線性實數，W_max是初始的權重值，W_min是最終的權重 值，iter_max是最大的迭代數，l是目前迭代數。c 及₁ c 是兩個正數，通常₂ 1 2 2 c =c = ，rand()及 Rand()產生(0,1)的隨機變數。 粒子群參考粒子本身最佳解位置，及粒子群最佳解位置，經由公式計算，得到下 一個移動目標，經由不斷重複此過程，使得粒子群往最佳解方向移動。 粒子群演算法流程如下： 步驟一：粒子初始化，以隨機方式在解空間中初始化粒子的速度及位置。 步驟二：評估，依據評估函數，求出粒子的評估值。 步驟三：計算粒子的下一個移動方向，依據粒子本身的最佳解，及粒子群最佳 解，帶入公式得到下一個移動方向。

步驟四：更新粒子位置。

檢查是否達到停止條件，是則停止演算法，否則至步驟二。

2.2 直交實驗設計

2.2.1 直交表

直交表 (orthogonal array) 是由 R. A. Fisher 最先提出的，直交所代表的意 思是平衡 (balance) 而不混合 (mix) ，亦即統計上的獨立 (statistically

independence) ，因此直交表中每一欄的各水準值 (level) 出現次數是相同的， 使用直交表，事實上僅是進行部份因素實驗 (fractional-factorial experiment) ， 因此能較完全因素實驗 (full-factorial experiment) 節省大量執行的時間，且直交 實驗具有系統推理的特性，因此只需進行部份因素實驗就可以求得最佳解的近 似解 (near optimum) [8] [9] 。 以兩水準，三因素直交表說明，如表 2.1 所示，若要進行完全因素實驗， 需要八次實驗(₂3 _{= )，如果需要在八次實驗中選擇只作四次實驗，如何選擇能8} 達到均勻取樣的目的，建構一個L₄(2 )3 的直交表，如表 2.2 所示，可以縮減成 四次實驗，這樣的取法，如果以六面體的立體空間來看，如圖 2.1，選擇的實 驗點是1、4、6 與 7，六面體的每一面都有兩個實驗點，而且都是對稱的，可 保證最佳解在其所包圍的立方體之中，使用均勻且對稱的取樣來推測全部實驗 的最佳解。 表 2.1 兩水準三因素完全實驗 Factors Experiment Number x 1 x 2 x 3 1 0 0 0 2 0 0 1 3 0 1 0

4 0 1 1 5 1 0 0 6 1 0 1 7 1 1 0 8 1 1 1 表 2.2 兩水準三因素直交實驗表 Factors Experiment Number x 1 x 2 x 3 1 0 0 0 2 0 1 1 3 1 0 1 4 1 1 0 圖 2.1 兩水準三因素空間分佈圖

2.2.2 兩水準直交表的產生方式

以兩水準直交表L₈(2 )7 為例說明直交表產生方法，程序如下： 1. 當因素個數為N 時，完全因素實驗為 2N ，直交表大小為M 列乘以 M-1 行， 標示為 ₍₂M 1₎ M L − ，其中(_M =_L[log (2 N+1)])_M =2⎡⎢log (2 N+1)⎤⎥。 2. 將a 因素放入第 1 行位置。水準值 1 和水準值 2 連續出現的次數為 8₁ 4 2 = 。

3. 將b 因素放入第 2 行位置，水準值 1 與水準值 2 連續出現的次數為 8₂ 2 2 = 。 4. 第3 行為 a ×b。即當 a = b = 1 或 a = b = 2 時 a ×b = 1，否則 a ×b = 2。 5. 將c 因素放入第 4 行位置，水準值 1 和水準值 2 連續出現的次數為 8₃ 1 2 = 。 6. 第5、6 與 7 行依步驟 3 類推。 必須注意的是：當N 值為 4、5、6、7 時，都使用 7 8(2 ) L 直交表，但忽略M-N-1 行的使用。而每一行的(1, 1)、(1, 2)、(2, 1)與(2, 2)四對數值都以同樣的次數出 現。 而根據應用的不同，也將使用不同水準的直交表，例如：三水準的直交表 或更高水準的直交表。

2.2.3 多水準直交表產生方式

定義直交表 ( N) M L Q ，N 為 factor 數，Q 為水準數，水準數為奇數，M 為 直交表的列數， J M =Q ，J 為符合 1 1 J Q N Q − = − 的整數，定義OA 為[ai j M N, ] × 的陣 列。建構多水準直交表依序下列三步驟[10]，

1. 首先建構直交表的基礎行(basic column)，其中 basic column 為a ： j

2 ₁ 3 ₁ 1 ₁ 1, 2, 1, 1,..., 1 1 1 1 J Q Q Q j Q Q Q − − − − = + + + − − − 建構basic column： for k=1 to J do begin 1 ₁ 1 1 k Q j Q − ₋ = + − for i=1 to J Q do , 1 i j J i a Q k ⎢ − ⎥ = ⎢ ₋ ⎥ ⎣ ⎦mod Q end

2. 建構basic column 以外的行(nonbasic columns)： for k=2 to J do begin 1 ₁ 1 1 k Q j Q − ₋ = + − for s=1 to j-1 do for t=1 to Q-1 do ( 1)( 1) ( ) j s Q t s j a _{+ − − +} = a × +t a mod Q _i end 3. 最後步驟：a 每一次增加一，針對1_{i j,} ≤ ≤i M,1≤ ≤ ，完成整個多水準j N 直交表。

2.2.4 因素分析

使用直交表進行的取樣和實驗結果進行因素分析。令y 表示為_t 7 8 L (2 ) 直交 表實驗中第 t 次實驗的評估函數值，則第 j 個因素水準值 k 的主效果S 定義_jk 為： jk 1 S n _{t tjk} t y F = =

∑

i (2-10) 其中F 為一個旗標值，若第 t 次實驗中第 j 個因素選用水準為 k ，則_tjk F _tjk 為 1；若否，則F 為 0。若適應函數為望大，則較大的主效果值表示對適應 tjk 函數具有較佳的貢獻度；反之若適應函數望小，則主效果值小者貢獻度較佳。 主效果可以顯示因素中水準的各別影響。例如主效果 S_j1>S_j2 則表示在參數 最佳化的問題中，第 j 個因素水準值 1 對於整體最佳化函數的貢獻大於水準 值 2 。如果相反的情形Sj₁<Sj₂，則表示水準值 2 較佳。每一個因素的較佳

水準組合成一個新解，此解為推理解。

2.2.5 直交實驗

科學實驗的過程，通常利用假設來減少實驗結果的因素個數，以節省時 間，應用直交實驗設計也是為了解決此問題而被提出的方法之一。Orthogonal Experimental Design, OED 主要包含兩個重要的部份：直交表(Orthogonal Array, OA)與因素分析(Factor Analysis)[11][12]。首先透過直交表，產生出獨立且均衡 的每一個因素，再藉由每一個因素分析出的主效果(Main Effect)，由主效果推論 每一個因素對於該實驗結果的優劣。因此以直交實驗來解最佳化問題時，問題 的一個參數可視為直交實驗中的一個因素，而參數視為因素的水準(Level)值。 完全因素實驗(Complete Factorial Experiment)會以全部水準值的排列組合進行

實驗，而OED 僅取全部排列組合中的一部份來進行分析實驗，也就是部份因

素實驗(Fractional Factorial Experiment)，因此直交陣列系統推理化的特性只需進 行部份因素實驗就可以推測出所有搜尋空間中最佳的近似解(Near Optimum)， 可節省大量執行的時間。

2.3 Local Search

Local Search 的方式，使用最大速度當作偏移量的基準，算出要搜尋的位置， 用新的位置取得評估值，如果結果比較好，使用新位置取代舊的位置，如果連續 兩次都搜尋成功，放大最大速度，如果連續兩次都失敗，則縮小最大速度，朝另 一個方向搜尋。這樣的方式比傳統的local search 更有效率，可以克服粒子群演 算法的移動缺點。

2.4 智慧型粒子移動機制步驟

智慧型粒子移動機制步驟使用兩水準的直交表進行直交實驗，找出最佳的移

動方向，直交表因素數由問題的維度決定，智慧型粒子移動機制步驟如下： 1. 使用目前解 X 產生一個暫時解X ，暫時解產生經由全域最佳解資訊。 ₁ 2. 將 X 與X 分割成 N 個參數的群組，每一個群組視為一個因素。 ₁ 3. 使用直交表 ₍₂(M 1)₎ M L − 的第一個N 列， 2log (2 N 1) M = ⎡⎢ + ⎤⎥。 4. 使用因素 i 的水準一和水準二，表現出 X 與X 的第 i 個群組。 ₁ 5. 計算產生組合的評估值。 6. 計算主效果。 7. 依據主效果決定每一個因素的最佳水準。 8. 候選解由最好的群組組成。 9. 驗證推理解是否與原本解相等，如為是，選直交實驗中最好的一個來當新解 候選解。如為否，在推理解與直交表所做的N 次實驗中挑選最好的一個來當 新解候選解。

2.5 Dynamic Multi-Swarm Particle Swarm Optimizer with Local

Search 介紹

Dynamic Multi-Swarm Particle Swarm Optimizer with Local Search (DMS-L-PSO)延續使用 Dynamic Multi-Swarm Particle Swarm Optimizer

(DMO-PSO)[13]，加上使用 Quasi-Newton method 的 local search。在演化過程 中，產生大的變異度與演算法收斂速度加快是互相抵觸的，為了達到有較大的變 異度，使用DMS-PSO，為了達到快速收斂而加入 local search 特性。DMO-PSO 的運作方式，初始化 m*n particles，隨機分成 n swarms，每個 swarm 有 m 個 particles，經過 regroup 的週期後在隨機重組這些 swarms，用實驗找出最好的 swarm’s population size 及 regrouping period。DMS-L-PSO，使用 DMO-PSO，加 上 local search，經過 L 迭代後，排序所有群組，取前 25% 作 local search。 DMS-L-PSO 可以提供更大的變異度，經由粒子及群組的分裂跟重新結合，分享

粒子跟群組間的資訊，平衡全域跟區域搜尋的效果，在複雜的問題上，可以有好 的搜尋效果。

2.6 Orthogonal Particle Swarm Optimization(OPSO)介紹

OPSO 使用基礎的 PSO，在尋找下一個移動方向的時候，使用智慧型粒子 移動機制，加入直交表系統化的分析，增加找到最佳解的效能，因為直交實驗花 費較高的評估次數，演算法的粒子數目跟切割直交表的因素數都需經過考慮。 OPSO 的智慧型粒子移動機制，使用直交實驗找出潛在最佳解，可以使用較少的 粒子數目，達到很好的搜尋效果，尤其在large problem 的時候，效果越好。

2.7 基因演算法與 GPPSO 比較

2.7.1 基因演算法簡介

基因演算法(Genetic Algorithms, GAs) 為演化式演算法，基因演算法也是解 最佳化問題的演算法之一。基因演算法為模擬物種基因的繁衍機制，保留好的基 因，增加變異度適應新環境。圖 2.2 為基因演算法基本流程。

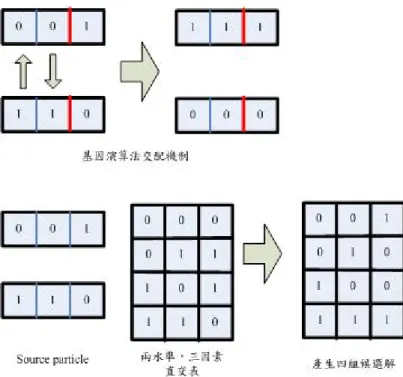
圖 2.2 基因演算法基本流程 基因演算法的基礎流程有：初始化、評估、選擇、交配及突變。初始化方式 根據基因編碼方式隨機初始化。評估根據評估函數計算得到評估值。選擇的目的 為保留好的個體(individual)基因特性，也保留住演化的結果，選擇的概念為，根 據一個選擇機率，以好的個體取代不好的個體。交配架構在前代優秀的基因上， 期望創造出更多更好的基因，交配的一種方式為單點交配，如圖 2.3 所示，隨機 挑選兩個親代，隨機選取交配點，互換兩親代交配點兩側的基因，形成新的子帶， 計算親代與子代的評估值，選取兩個最好的當成原有的親代個體，交配的數量依 據交配率。

圖 2.3 基本交配機制 突變的目的為提高個體間的變異度，個體間的變異度除了從交配機制得來， 另一個重要來源便是突變，突變有很多方式，簡單的突變，選取單點依據染色體 編碼方式進行染色體突變，如圖 2.4 ，突變的數量由突變率決定。 圖 2.4 基本突變機制 由基因演算法流程可以看出，維持個體變異度是基因演算的重要機制，藉由變異 跟保存好的基因，慢慢朝最有利的方向演進。

2.7.2 傳統基因演算法與粒子群演算法的操作對應

傳統的基因演算法有選擇、交配與突變的機制，粒子群演算法沒有類似的 操作名稱，但是粒子群演算法中有相似的概念存在。基因演算法中的交配機制， 隨著迭代變化，縮小搜尋的範圍，交配也變的比較沒有效率，粒子群演算法中 沒有交配機制，對應基因演算法中交配的概念為，粒子群演算法可能隨機的超 越之前最好的位置，朝向全域或區域最佳解前進，且交配的觀念也顯露在粒子 與群體間分享訊息。

基因演算法中的突變，當演算法趨於收斂時，突變也不容易產生比目前更 好的解，粒子群演算法的最大速度設定，變化最大速度，可以讓粒子有機會到 達解空間的任何一個地方，最大速度的概念可對應基因演算法中的突變機制， 且粒子群演算法中的方向改變也可視為突變的一種表現方式。

2.7.3 傳統基因演算法與粒子群演算法的相異之處

首先，基因演算法中的選擇(selection)是適者生存的概念，保留最好的染色 體，粒子群演算法沒有這樣的操作，每個粒子一直存在，粒子的位置依據之前 的位置改變。其二，基因演算法的交配，隨機選取親代，互換兩親代的基因， 粒子群演算法粒子間不互換特性，但是互相分享資訊，粒子群演算法中粒子的 影響來自自己的最好解，跟區域或全域最好解，被影響的因素不是來自隨機的。 其三，粒子群演算法會記憶個體的最好解，提供粒子群的搜尋方向。 基因演算法的初始化方式為，將要解決問題的參數編碼為染色體，每一染 色體即為解空間的一個潛在解，基因演算法的染色體對應粒子群演算法的粒 子，相異於粒子群演算法的初始解，基因演算法的初始化編碼可以適用於binary 及實數問題，粒子群演算法因初始化的關係較適合解實數問題。

三、提出

GPPSO 方法論

3.1 想法起源

在不同領域的應用範圍求解最佳化問題，通常會根據應用的內容，挑選合適 的演算法，加上對應用問題的相關背景知識進行演算法的調校及修正。如何發展 一種通用型的演算法，在個領域範圍上都有不錯的效能表現，是最初的想法。不 同領域中，遇到的問題可能有，求解問題有交互作用，多個區域解以及要解大參 數的問題，針對可能遇到的問題，在演算法中加入可以解決的機制，挑選使用粒 子群演算法，加入三種不同機制，期能達到成為一通用型的粒子群演算法。 首先，粒子群演算法初始化為在解空間中隨機產生初始粒子族群，使用初始 解開始演算法計算，如果能在初始化時，使用直交實驗，有系統的求出初步最佳 解，對正確解的搜尋有縮短時間的幫助。其次，粒子群演算法的缺點有容易掉入 局部最佳解(local optima)的問題，且針對搜尋空間大、大參數(large search space) 的問題時，不容易找到最佳解。Local search 機制，可以針對單獨粒子操作，當 粒子位置不是區域最佳解時，使用local search，可以在鄰近區域內找到區域最佳 解，且粒子的位置改變，不需與粒子群分享訊息，可以增加粒子間的變異度，增 加粒子間的變異度可以提高搜尋效能，改善整體搜尋時間。最後，針對大參數時， 對單點粒子進行智慧型粒子移動機制，利用直交表的系統推理得到較佳的下一個 粒子位置，可以減低成本，達到更好的搜尋目的。

有別於標準的PSO，擬加入 ODE 機制求初始粒子族群，並使用 IMM 針對

大參數問題，期望IMM 中有系統的推理，可以更有效的找出潛在最佳解，最後

為了達到general-purpose 的目標，對於可能的參數群，加以利用 ODE 去產生參 數的最佳組合，提供一組預設的演算法參數。

3.2 理論基礎

機方式產生初始點，在搜尋空間中隨機選擇初始點，產生的問題可能有，初始化 的點對解空間取樣不夠均勻。取樣不均勻需要花費較高的成本找到最佳解，隨機 因素可能產生演算法不夠穩定，也可能產生搜尋效果不夠好的結果。初始點的位 置，影響搜尋速度跟搜尋結果。 使用直交表進行初始粒子位置的選取，採用直交表進行取點動作，透過直交 表的有效直交實驗，對解空間均勻取點，減少因為隨機初始化產生的不穩定。初 始化時，有效且公平的選擇初始點，將粒子群體導向最佳解方向，期望達到穩定， 快速收歛的目標。 使用直交表得到初始解的概略方式為，對解空間分析後，設定直交表使用的 水準數，直交表使用的水準數即為對解空間的分割數，得到直交表後，針對每一 個解進行計算，取得評估值，對所有的解取最好的前N 個解，N 為粒子群演算法 的粒子數目，使用這些粒子最為演算法的初始粒子族群。直交表初始化可以減少 隨機初始化的不確定因素。直交表特性可以保證均勻取點，雖然隨機也是強調均 勻撒點，使用直交表可以更有系統的得到初步的最佳解。直交表的水準數，也關 係到直交初始化的效能。水準數太少不夠均勻，甚至可能掉在局部最佳解(local optima)，水準數太多則經濟效益不佳。以平均有系統的選擇初始點，可以減少每 個點的搜尋空間，加快演化收斂速度，期望解決求解不穩定的問題。 使用直交表協助產生初始解，採用多水準的直交表，因多水準的直交表可以 將解空間分割成多個等分，如只使用兩水準直交表，雖然評估的次數較少，但得 到的精確度卻大幅降低。如解空間大的時候，只對解空間取兩點來考慮，喪失使 用直交表均勻取點的特性，也沒有辦法確實得到較佳的初始解。

當粒子位置不是local optima 時，使用 local search 可以在鄰近區域找到比目 前更好的解。很多研究指出，維持粒子間的變異度可以提升粒子群演算法的效 能，一個有效的方式為在粒子群演算法中加入突變的操作，local search 可以改變 粒子的位置，維持粒子間高的變異度，也不影響其他的粒子，local search 類似突 變操作的功能，可以維持粒子間的變異度，防止演算法過早收斂。

粒子群演算法解large 問題時，效果不佳。OPSO 可解 large 問題，OPSO 對 每一個粒子均進行直交實驗，花費成本很高。改良針對一個最好的粒子作智慧型 粒子移動機制，可以降低成本，達到更好的搜尋目的。 為達到general-purpose 的目的，將影響粒子群演算法搜尋效果的參數當成直 交表因素，帶入直交表，經由直交實驗，得到最好的一組預設參數。評估函數使 用代表型函數，最後評估值為所有測試函數的評估值總和。目前使用的參數有， 初始化直交表的水準數、最大的粒子移動速度以及慣性權重(W)。挑選參數的原 因，初始化直交表的水準數影響評估次數，也影響初始化取點的密度。粒子群演 算法對最大的粒子移動速度敏感，當最大速度過大時，每次速度的改變都會超過 預估可能下一個較好解的範圍，演算法會趨近random search，當最大速度過小 時，每次移動的範圍太小，容易成為local search。慣性權重維持區域搜尋與全域 搜尋的平衡。

3.3 GPPSO 之設計

3.3.1 GPPSO 流程

GPPSO 的流程如下， 1. 使用直交表得到粒子初始解 2. 標準 PSO 流程 3. local search 機制

4. modified IMM，如粒子總數為 30，將粒子排序之後，找最好的前 10 個 particle 進行直交實驗

圖 3.1 GPPSO 流程

3.3.2 由直交實驗求出 GPPSO 參數

為達到general-purpose 目的，本方法先要設定參數值，包括使用直交表 初始化的直交表參數：水準數(level)、慣性權重(w)及粒子移動最大速度。粒 子群演算法的參數，影響搜尋效能，期望能找出一組通用的參數，在一般通 用的問題上，都有不錯的效能。使用三因素，三水準直交表，進行獨立實驗 二十五次。選取參數分別為初始化直交表水準數，最大速度及W。初始化直 交表水準數三水準分別為，5，11，13。最大速度，三水準分別為，3，5，7。 W，三水準分別為，0.3，0.5，0.7，使用上述參數，帶入三乘三的直交表，有 九次直交實驗，取得最後平均最佳的一組參數，當作預設的參數。

3.3.3 GPPSO 的方法全貌敘述

3.3.3.1 直交表初始化

GPPSO 方法擺脫傳統 PSO 方法用隨機取點當作初始解，操作直交表方 法更有效率取得較好的初始解，直交表方法的觀念是從解域中所有可能的解 (possible solution points)去排出少數且獨立的潛在解去做最佳解的評估比較， 以其中最好的解，當作初始解，使用直交表求初始解步驟如下， 1. 建構直交表。直交表因素數為問題的維度(dimension)，直交表水準數為對 解範圍要切割密度，如水準數為三，將解範圍切割成等分，取三個代表點， 分別代表水準一、水準二及水準三。 2. 依據直交表初始化，如水準數為一時，選取第一個等分的代表點。得到所 有粒子位置後，帶入評估函數，求得評估值，依據評估值及直交表，導出推 理解。根據評估值排名，取前N 個作為演算法初始值。N 為原始 swarm 的 particle 數目。

3.3.3.2 Local search

Local search 目的為探索更好的潛在解，並提供更大的變異度，步驟如 下， 1. 步驟一：選定一個移動方向 ，得到新的位置 2. 步驟二：取得新位置的評估值 3. 步驟三：檢查評估值是否有比原始解的評估值好，如是，則往同一方向繼 續進行，如否，則朝其他方向搜尋 停止條件，設定local search 可執行的最大步數，超過此最大步數即停止，如 朝多個方向搜尋失敗，即跳出local search 步驟。

GPPSO 中的 local search 機制，只使用最好的粒子進行 local search，可 提供好的效能，也可節省評估次數。

d xil d xil 1

+

3.3.3.3 智慧型粒子移動機制

Novel Orthogonal Particle Swarm Optimization 中針對所有 particle 作智慧 型粒子移動機制，因為智慧型粒子移動機制需要評估成本很高，所以需降低 particle 數量，adopted PSO 中採用針對最好的前幾個 particle 做智慧型粒子移 動機制，降低評估成本也可以求得很好的效果。 取得目前最好的兩個particle 當作直交實驗的來源，帶進直交表中，求得 最好的結果，如果結果優於原始最好的particle，進行取代最好的 particle。

3.4 GPPSO 與基因演算法的操作對應

基本的粒子群演算法，沒有選擇，交配，突變的機制，經由計算得到下一個 最佳解位置，如何維持粒子間的變異度，為很多研究的目標，本篇論文中，提出 local search 跟 IMM，維持粒子間變異度，對照基因演算法的突變跟交配機制。 GPPSO 加入 local search 機制，local search 在粒子附近搜尋，找出更好的 解，增加粒子間的變異度，模擬基因演算法的突變機制，增加個體間的變異度， 小幅度的變化，試圖找出更好的解。 GPPSO 加入 IMM 機制，可對應基因演算法的交配機制，交配產生不同的 個體，評估個別個體的評估值，挑選好的取代原親代，IMM 經由直交表產生不 同的個體樣本，可得到N 個不同的候選解及一個推理解(N 為直交表直交實驗 數)，經由評估函式，選取最好的解取代原始解，如圖 2.5。

四、實驗結果與效能分析

此章節中，分別描述使用的測試函數介紹，以及實驗設計和實驗結果。測試函數介 紹CEC 2005 special session 的內容，以及論文”OPSO: Orthogonal Particle Swarm

Optimization and Its Application to Task Assignment Problems”中使用的十二個的測試函

數。接著介紹實驗設計，實驗分成八個部份，第一部份為取得GPPSO 的預設參數，考

慮影響GPPSO 效能的變異參數，由實驗結果推得平均效能最佳的一組參數，當成預設

參數。第二部份，分別加入三個機制，由實驗結果證明，分別加入的機制，對於搜尋效 能，都有達到預期的目標。第三個實驗部份為使用CEC 2005 special session 的實驗結果。 第四部份，使用CEC 2005 special session 作為測試函數，比較 GPPSO 與 DMS-L-PSO 的 實驗數據比較。第五部份，比較同為使用CEC 2005 special session，已發表的論文結果 進行評比。第六部份，GPPSO 與 OPSO 比較，使用論文”OPSO: Orthogonal Particle Swarm Optimization and Its Application to Task Assignment Problems”中的十二個的測試函數。第 七部份，列出GPPSO 於 CEC 2005 special session 上的複雜度。第八部份，使用 CEC 2005 special session 作為測試函數，比較分別加入三個機制的收斂速度比較，由實驗結果得 到，GPPSO 的收斂速度最快。

4.1 測試函數介紹

使用兩個測試函數，分別為CEC 2005 special session (IEEE Congress on Evolutionary Computation of the Special Session on Real-Parameter Optimization) [14]

在2005 年所提供的一系列標準測試函式，在衡量演算法的效能上使用有系統性的

方式來做評判，可客觀地對於演算法的效能上做分析與探討，此測試函數的定義置 於附錄一；以及論文”OPSO: Orthogonal Particle Swarm Optimization and Its

Application to Task Assignment Problems”中使用的十二個的測試函數，測試函數表 4.27。

‧ Unimodal Functions (5): Basic Functions (5)

F1: Shifted Sphere Function

F2: Shifted Schwefel’s Problem 1.2

F3: Shifted Rotated High Conditioned Elliptic Function F4: Shifted Schwefel’s Problem 1.2 with Noise in Fitness F5: Schwefel’s Problem 2.6 with Global Optimum on Bounds ‧ Multimodal Functions (20):

Basic Functions (7):

F6: Shifted Rosenbrock’s Function

F7: Shifted Rotated Griewank’s Function without Bounds

F8: Shifted Rotated Ackley’s Function with Global Optimum on Bounds F9: Shifted Rastrigin’s Function

F10: Shifted Rotated Rastrigin’s Function F11: Shifted Rotated Weierstrass Function F12: Schwefel’s Problem 2.13

Expanded Functions (2):

F13: Expanded Extended Griewank’s plus Rosenbrock’s Function (F8F2) F14: Shifted Rotated Expanded Scaffer’s F6

Hybrid Composition Functions (11): F15: Hybrid Composition Function

F16: Rotated Hybrid Composition Function

F17: Rotated Hybrid Composition Function with Noise in Fitness F18: Rotated Hybrid Composition Function

F19: Rotated Hybrid Composition Function with a Narrow Basin for the Global Optimum

F20: Rotated Hybrid Composition Function with the Global Optimum on the Bounds

F21: Rotated Hybrid Composition Function

F22: Rotated Hybrid Composition Function with High Condition Number Matrix

F23: Non-Continuous Rotated Hybrid Composition Function F24: Rotated Hybrid Composition Function

F25: Rotated Hybrid Composition Function without Bounds

表 4.1 測試函數列表

Test function

x

_i Optimum D=100 Dimension 1 1 2 [sin( ) sin( )] 3 D i i i x F x = = −

∑

+ [3,13], 1, 2,..., i x i D ∈ = 1 max ( ) 121.598 F = 1 1 2 1 1 2 [sin( ) sin( )] 3 D i i i i i x x F x x − + + = = −

∑

+ + [3,13], 1, 2,..., i x i D ∈ = ( )F2 max =200 1 2 3 1 0.5 D i i F x − = =

∑

⎢_⎣ + ⎥_⎦ [-100, 100], 1, 2,..., i x i D ∈ = ( )F3 min =0 2 4 1 10cos(2 ) 10 D i i i F x πx = ⎡ ⎤ =

∑

_⎣ − + _⎦ [-5.12, 5.12], 1, 2,..., i x i D ∈ = ( )F4 min =0 2 5 1 D i i F x = =

∑

[-5.12, 5.12], 1, 2,..., i x i D ∈ = ( )F5 min =0 6 1 ( sin(10 )) D i i i F x πx = =

∑

[-1.0, 2.0], 1, 2,..., i x i D ∈ = 6 max ( )F =1.85D 7 1 sin(10 ) 10 D i i i x F x π π = =

∑

[-0.5, 0.5], 1, 2,..., i x i D ∈ = ( )F7 min =0 2 8 1 1 1 1

20 exp(1) 20exp( 0.2 ) exp( cos(2 ))

D D i i i i F x x D = D = π = + − −

∑

−

∑

[-30, 30], 1, 2,..., i x i D ∈ = ( )F8 min =0

9 1 418.9829 sin( ) D i i i F D x x = = −

∑

[-500, 500], 1, 2,..., i x i D ∈ = ( )F9 min =0 1 2 2 2 10 1 1 100( ) ( 1) D i i i i F x x x − + = ⎡ ⎤ =

∑

_⎣ − + − _⎦ [-5.12, 5.12], 1, 2,..., i x i D ∈ = (F10 min) =0 11 1 6 D _i i F D x = = +

∑

⎢ ⎥_{⎣ ⎦} [-5.12, 5.12], 1, 2,..., i x i D ∈ = (F11 min) =0 2 12 1 1 cos( ) 1 4000 D D i i i i x F x i =− = =

∑

−

∏

+ [-600, 600], 1, 2,..., i x i D ∈ = (F12 min) =0

4.2 實驗說明

利用GPPSO 來找函數最佳解，假設給定函數及解範圍如下，維度(dimension, D) 為5，求函數最小值 GPPSO 的流程如下： 步驟一：使用直交表求初始解，使用三水準直交表，將解空間切割成三等分，解 範圍為 -2.56, 0, 2.56，採用三水準、因素數為 5 (使用直交表因素(factor)數等於測 試函數的dimension 數)的直交表進行值交實驗，經由計算使用 的直交 表，評估直交實驗的27 個候選解及一個推理解，排序後取前 N 個解當粒子初始 族群，N 為演算法使用的粒子數目。 步驟二：評估，假設其中一個粒子位置為 帶入評估函數，求得 步驟三：改變粒子位置及速度，根據公式計算下一個粒子位置及速度。 步驟四：Local search，根據最大速度計算出隨機擾亂的距離， 步驟五：Modified IMM 步驟六：測試演算法是否停止 2 i 1 ( ) , x [ 5.12,5.12], i=1,2,...,D D i i F x x = =

∑

∈ − 13 27(3 ) L 1 2 3 4 5 1 ( , , , , ) ( 2.56, 2.56, 2.56, 2.56, 2.56)1 1 1 1 1 x = x x x x x = − − − − − 2 2 2 2 2 ( ) ( 2.56) ( 2.56) ( 2.56) ( 2.56) ( 2.56) 32.768 F x = − + − + − + − + − =

4.3 實驗設計

4.3.1 PSO 的預設參數

相關參數有：

1. 粒子群數目(number of particle)，由 dimension 決定，dimension 越高，粒子 群數目應該越高。

2. 慣性權重(inertia weight, W)，用於計算粒子速度，平衡全域搜尋與區域搜尋。

3. C ，₁ C ，通常使用常數 2。 ₂

4. 最大的粒子移動速度(maximal velocity, V_max)，最大粒子移動速度如太大，演 算法會 成為隨機搜尋，如太小，會成為區域搜尋。 提出的演算法，還有一個參數為均勻取樣取初始解使用的直交表水準數，使用的 直交表水準數相對應於對解空間的切割程度，分割的越細，需要的評估次數越 多，越容易找到較好的初始解。 利用這三個參數，帶入直交表中，使用三變數，三水準的直交表進行實驗，實驗 取直如下表。三個參數分別為直交表水準數，最大的粒子移動速度以及慣性權 重，實驗使用固定的粒子個數。 直交實驗取第一個因素是初始化直交表水準數，第二個因素為粒子移動的最大速 度，第三個因素是慣性權重。 表 4.2 直交實驗的參數表 求初始解使用的直交表水準數 最 大 的 粒 子 移 動 速度(V_max) 慣性權重(w) Level 1 N = 11 3 3 Level 2 N = 13 5 5 Level 3 N = 17 7 7

表 4.3 4 9(3 ) L 的直交表 1 1 1 1 1 2 2 2 1 3 3 3 2 1 2 3 2 2 3 1 2 3 1 2 3 1 3 2 3 2 1 3 3 3 2 1 其中Factor 1：求初始解使用的直交表水準數，Factor 2：最大的粒子移動速度 (V_max)，Factor 3：慣性權重(w)。 表 4.4 Dimension = 10，依據直交表產生的統計結果 Factor 1 Factor 2 Factor 3 Fitness value

11 3 3 5 11 5 5 1 11 7 7 0 13 3 5 4 13 5 7 1 13 7 3 8 17 3 7 0 17 5 3 7 17 7 5 3 表 4.5 Dimension = 10，因素分析

Factor 1 Factor 2 Factor 3

Level 1 6 9 20

Level 2 13 9 8

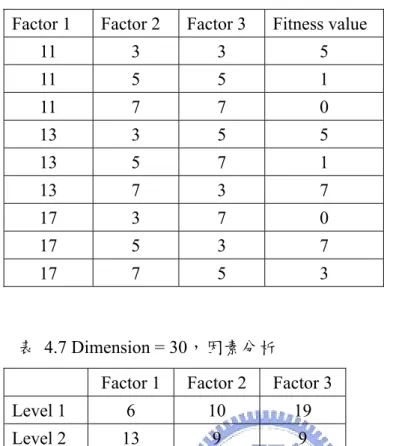
表 4.6 Dimension = 30，依據直交表產生的統計結果 Factor 1 Factor 2 Factor 3 Fitness value

11 3 3 5 11 5 5 1 11 7 7 0 13 3 5 5 13 5 7 1 13 7 3 7 17 3 7 0 17 5 3 7 17 7 5 3 表 4.7 Dimension = 30，因素分析

Factor 1 Factor 2 Factor 3

Level 1 6 10 19 Level 2 13 9 9 Level 3 10 10 1 實驗結果， 當dimension = 10 時，參數的配置為，初始化使用的直交表水準數為 13；最大的 粒子移動速度為7；慣性權重(w)為 3。 當dimension = 30 時，參數的配置為，初始化使用的直交表水準數為 13；最大的 粒子移動速度為3 及 7；慣性權重(w)為 3。 找出一組預設參數，選取的預設參數為：初始化使用的直交表水準數:13，最大的 粒子移動速度:7，慣性權重(w):3。 實驗數據為二十五次獨立實驗取平均值。 表 4.8 dimension = 10 直交表實驗數據(一) GPPSO (11, 3, 3) GPPSO (11, 5, 5) GPPSO (11, 7, 7) GPPSO (13, 3, 5) GPPSO (13, 5, 7) F 1 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00

F 2 7.31E-14 5.68E-14 1.28E-13 7.31E-14 7.31E-14 F 3 1.15E-12 1.37E-11 9.46E-07 3.11E-11 5.55E-09 F 4 5.20E-02 3.46E-01 2.39E+01 2.42E-01 9.17E+00 F 5 0.00E+00 0.00E+00 0.00E+00 0.00E+00 0.00E+00 F 6 1.14E+00 1.34E+00 4.99E-01 5.70E-01 1.14E+00 F 7 5.94E-02 6.53E-02 4.25E-02 6.08E-02 6.26E-02 F 8 2.04E+01 2.02E+01 2.03E+01 2.03E+01 2.03E+01 F 9 5.69E+00 4.12E+00 6.16E+00 3.98E+00 5.40E+00 F 10 5.83E+00 9.10E+00 9.33E+00 6.96E+00 9.67E+00 F 11 2.67E+00 2.89E+00 3.54E+00 3.26E+00 4.09E+00 F 12 1.30E+01 1.76E+01 8.64E+01 8.94E+00 5.81E+00 F 13 7.89E-01 7.06E-01 9.41E-01 6.52E-01 1.02E+00 F 14 2.33E+00 2.91E+00 3.14E+00 2.65E+00 2.99E+00 F 15 3.46E+02 3.65E+02 3.50E+02 2.53E+02 3.52E+02 F 16 1.08E+02 1.11E+02 1.17E+02 1.10E+02 1.17E+02 F 17 1.75E+02 2.02E+02 2.06E+02 1.71E+02 1.98E+02 F 18 5.63E+02 6.19E+02 7.20E+02 4.79E+02 3.10E+02 F 19 7.29E+02 8.65E+02 5.45E+02 6.78E+02 4.76E+02 F 20 4.59E+02 5.37E+02 6.57E+02 4.59E+02 6.15E+02 F 21 4.29E+02 5.00E+02 5.50E+02 5.22E+02 4.71E+02 F 22 7.92E+02 7.94E+02 8.03E+02 7.56E+02 7.79E+02 F 23 6.29E+02 5.59E+02 5.80E+02 5.59E+02 5.59E+02 F 24 3.07E+02 5.20E+02 4.85E+02 3.49E+02 4.15E+02 F 25 3.53E+02 3.82E+02 3.89E+02 4.01E+02 3.81E+02

Win rank 4 1 1 2 1 表 4.9 dimension = 10 直交表實驗數據(二) GPPSO (13, 7, 3) GPPSO (17, 3, 7) GPPSO (17, 5, 3) GPPSO (17, 7, 5) F 1 0.00E+00 0.00E+00 0.00E+00 0.00E+00 F 2 5.68E-014 8.84E-14 7.31E-14 4.87E-14 F 3 7.03E-012 8.25E-05 1.09E-12 1.01E-10 F 4 3.54E-001 1.75E+01 5.87E-02 1.52E+00 F 5 0.00E+00 0.00E+00 0.00E+00 0.00E+00 F 6 2.07E-08 4.43E-01 6.21E+01 3.56E-06 F 7 3.90E-02 7.35E-02 3.80E-02 4.82E-02

F 8 2.01E+01 2.04E+01 2.03E+01 2.01E+01 F 9 3.44E+00 4.54E+00 5.26E+00 6.28E+00 F 10 8.32E+00 7.74E+00 1.06E+01 1.01E+01 F 11 2.24E+00 4.91E+00 2.51E+00 2.70E+00 F 12 1.05E-09 3.61E+01 2.86E+00 8.04E+00 F 13 6.40E-01 8.11E-01 6.25E-01 1.03E+00 F 14 2.63E+00 2.96E+00 2.89E+00 3.18E+00 F 15 1.42E+02 2.22E+02 1.99E+02 1.60E+02 F 16 1.04E+02 1.04E+02 1.03E+02 1.16E+02 F 17 1.84E+02 1.90E+02 1.98E+02 1.82E+02 F 18 3.00E+02 6.89E+02 3.00E+02 5.30E+02 F 19 3.04E+02 6.96E+02 3.82E+02 6.34E+02 F 20 3.19E+02 7.67E+02 3.38E+02 6.41E+02 F 21 5.16E+02 5.00E+02 5.43E+02 5.00E+02 F 22 7.46E+02 7.78E+02 7.98E+02 8.04E+02 F 23 5.59E+02 5.77E+02 5.59E+02 5.59E+02 F 24 3.24E+02 6.25E+02 4.15E+02 6.33E+02 F 25 2.07E-08 4.25E+02 3.83E+02 3.83E+02

Win rank 11 3 4 2 表 4.10 dimension = 30 直交表實驗數據(一) GPPSO (11, 3, 3) GPPSO (11, 5, 5) GPPSO (11, 7, 7) GPPSO (13, 3, 5) GPPSO (13, 5, 7) F 1 1.01E-13 1.20E-13 1.20E-13 1.01E-13 1.07E-13 F 2 1.16E-07 5.18E-06 5.61E-05 2.08E-06 6.36E-05 F 3 6.35E-02 4.81E-01 2.96E+00 1.99E+00 3.16E+00 F 4 2.61E+04 3.70E+04 4.55E+04 2.80E+04 3.37E+04 F 5 1.33E+03 2.48E+03 2.93E+03 1.20E+03 1.75E+03 F 6 1.35E+00 1.47E+01 5.20E+01 3.78E+01 1.15E+02 F 7 1.59E-02 2.02E-02 2.40E-02 2.10E-02 2.45E-02 F 8 2.10E+01 2.10E+01 2.08E+01 2.10E+01 2.09E+01 F 9 5.35E+01 6.97E+01 7.78E+01 4.89E+01 6.71E+01 F 10 6.92E+01 8.88E+01 9.94E+01 7.13E+01 8.18E+01 F 11 2.44E+01 2.60E+01 2.47E+01 2.72E+01 2.85E+01 F 12 1.96E+04 2.17E+04 3.03E+04 2.84E+04 1.63E+04 F 13 3.61E+00 5.23E+00 6.14E+00 5.39E+00 5.31E+00

F 14 1.17E+01 1.20E+01 1.22E+01 1.19E+01 1.24E+01 F 15 3.70E+02 3.53E+02 3.75E+02 3.99E+02 3.48E+02 F 16 8.60E+01 1.59E+02 2.02E+02 1.65E+02 1.03E+02 F 17 2.89E+02 3.47E+02 4.13E+02 2.88E+02 3.12E+02 F 18 9.06E+02 9.07E+02 9.06E+02 9.06E+02 9.06E+02 F 19 9.06E+02 9.06E+02 9.06E+02 9.06E+02 9.06E+02 F 20 9.07E+02 9.07E+02 9.05E+02 9.05E+02 9.05E+02 F 21 6.35E+02 9.34E+02 1.03E+03 6.98E+02 7.33E+02 F 22 8.65E+02 8.85E+02 8.82E+02 8.71E+02 8.74E+02 F 23 8.30E+02 1.10E+03 1.10E+03 9.10E+02 1.10E+03 F 24 9.42E+02 9.54E+02 9.55E+02 9.52E+02 9.49E+02 F 25 2.19E+02 2.13E+02 2.16E+02 2.20E+02 2.15E+02

Win rank 5 1 2 2 1 表 4.11 dimension = 30 直交表實驗數據(二) GPPSO (13, 7, 3) GPPSO (17, 3, 7) GPPSO (17, 5, 3) GPPSO (17, 7, 5) F 1 1.06e-13 1.14E-13 1.33E-13 1.01E-13 F 2 4.42e-07 1.84E-04 5.77E-06 4.63E-05 F 3 5.82e-01 3.05E+00 2.21E-01 5.86E-01 F 4 3.36e+04 2.99E+04 3.17E+04 4.68E+04 F 5 1.93e+03 1.52E+03 1.12E+03 2.00E+03 F 6 6.78e+01 4.49E+01 8.87E-01 8.88E-01 F 7 2.87e-03 1.26E-02 9.02E-03 2.32E-02 F 8 2.09e+01 2.09E+01 2.10E+01 2.09E+01 F 9 5.82e+01 5.95E+01 6.03E+01 7.03E+01 F 10 6.30e+01 7.72E+01 6.71E+01 8.70E+01 F 11 2.58e+01 2.71E+01 2.58E+01 2.41E+01 F 12 6.56e+02 2.22E+04 1.32E+04 3.61E+04 F 13 2.94e+00 5.76E+00 3.50E+00 5.22E+00 F 14 1.19e+01 1.19E+01 1.22E+01 1.21E+01 F 15 3.52e+02 3.33E+02 3.85E+02 3.86E+02 F 16 1.22e+02 9.22E+01 1.39E+02 1.36E+02 F 17 3.29e+02 2.83E+02 3.29E+02 3.48E+02 F 18 9.05e+02 9.05E+02 9.07E+02 9.06E+02 F 19 9.05e+02 9.05E+02 9.07E+02 9.06E+02

F 20 9.06E+02 9.06E+02 9.07E+02 9.06E+02 F 21 1.10E+03 6.33E+02 8.31E+02 1.10E+03 F 22 8.62E+02 8.73E+02 8.75E+02 8.79E+02 F 23 1.04E+03 9.56E+02 1.08E+03 1.10E+03 F 24 9.47E+02 9.53E+02 9.63E+02 9.54E+02 F 25 2.13E+02 2.21E+02 2.15E+02 2.14E+02

Win rank 8 5 3 2

4.3.2 GPPSO 中個機制的實驗結果

4.3.2.1 單純的 PSO，與加入均勻取樣初始化的 PSO 的實驗結果比

較

使用直交實驗推理找出初始解，適用於當問題有交互作用時，使用測試函數 Function 6，Function 7，Function 13，Function 15，Function 18，Function 21， Function 24。由實驗結果可以看出，使用直交實驗推理找出初始解的效果較 好。 實驗參數，初始化使用的直交表水準數：13，最大的粒子移動速度：7，慣性 權重：3。 表 4.12 加入使用直交表求初始解的實驗數據 Dimension 10 PSO PSO + 直交實驗推理找初始解 Function 6 1.24E+03 5.24E+02

Function 7 2.36E-01 2.23E-01 Function 13 1.13E+00 7.62E-01 Function 15 3.93E+02 9.02E+01 Function 18 8.93E+02 8.61E+02 Function 21 4.85E+02 4.60E+02 Function 24 2.00E+02 2.00E+02

4.3.2.2 單純的 PSO，與加入 local search 的 PSO 的實驗結果比較

使用測試函數Function 5，Function 7，Function 13，Function 15。經由實驗結 果可以得到，加入 local search 平均可以增加搜尋效果。

實驗參數，初始化使用的直交表水準數：13，最大的粒子移動速度：7，慣性 權重：3。

表 4.13 加入 local search 的實驗數據

Dimension 10

PSO PSO +local search

Function 5 0.00E+00 0.00E+00 Function 7 2.36E-01 8.51E-02 Function 13 1.13E+00 1.15E+00 Function 15 3.93E+02 3.58E+02

Win rank 1/4 2/4

4.3.2.3 單純的 PSO，與加入 modified IMM 的 PSO 的實驗結果比

較

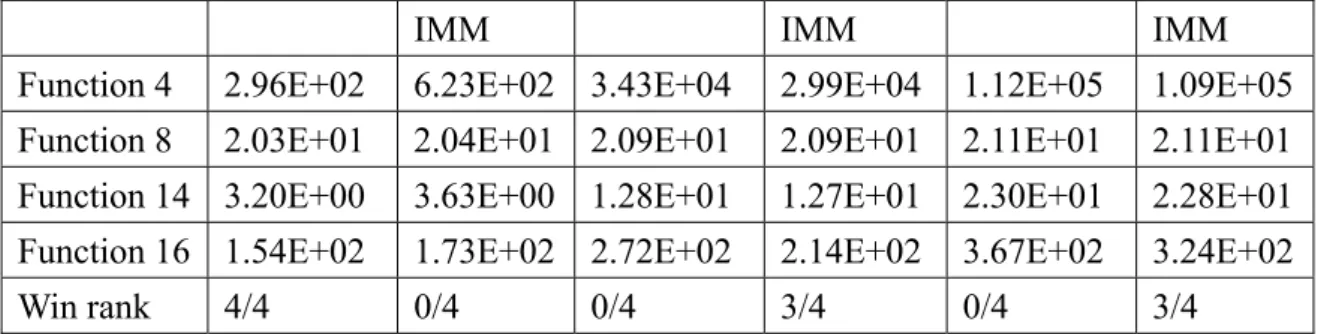
加入modified IMM(OPSO)，在 dimension 大的時候，可以看出效果，使用測 試函數Function 4，Function 8，Function 14，Function 16。由實驗結果得知， 當dimension 增大的時候，結果較好，當 dimension 小的時候，搜尋效果沒 有明顯增加，因dimension 小的時候，作 modified IMM 會增加評估次數。 實驗參數，初始化使用的直交表水準數：13，最大的粒子移動速度：7，慣性 權重：3。

表 4.14 加入 modified IMM 的實驗數據

Dimension = 10 Dimension = 30 Dimension = 50

PSO PSO + modified PSO PSO +modified PSO PSO + modified

IMM IMM IMM Function 4 2.96E+02 6.23E+02 3.43E+04 2.99E+04 1.12E+05 1.09E+05

Function 8 2.03E+01 2.04E+01 2.09E+01 2.09E+01 2.11E+01 2.11E+01 Function 14 3.20E+00 3.63E+00 1.28E+01 1.27E+01 2.30E+01 2.28E+01 Function 16 1.54E+02 1.73E+02 2.72E+02 2.14E+02 3.67E+02 3.24E+02

Win rank 4/4 0/4 0/4 3/4 0/4 3/4

4.3.3 CEC 2005 special session dimension 10 及 dimension 30 實驗

結果

表 4.14 至表 4.18 為 dimension 10 的實驗結果，表 4.19 至表 4.22 為 dimension 30 的實驗結果。

實驗參數，初始化使用的直交表水準數：13，最大的粒子移動速度：7，慣性 權重：3。

表 4.15 Dimension = 10，result of Function 1-5 Pro.

FES

1 2 3 4 5 1st 3.43E+001 2.31E+002 3.12E+004 3.99E+003 5.47E+002

7th _{8.21E+001 3.99E+002 3.85E+004 1.80E+004 1.06E+003}

13th _{1.08E+002 7.27E+002 4.30E+004 2.02E+004 1.16E+003}

19th _{1.10E+002 7.71E+002 4.62E+004 2.24E+004 1.24E+003}

25th _{1.38E+002 8.48E+002 4.77E+004 2.59E+004 1.65E+003}

Mean 1.35E+002 6.70E+002 4.77E+004 2.01E+004 1.23E+003

3

10

Std 7.17E+001 2.41E+002 1.06E+004 8.11E+003 3.84E+002 1st _{1.48E-002 2.84E-002 1.10E+003 7.45E+002 1.27E+000}

7th _{3.54E-002 1.23E+001 3.79E+003 1.52E+003 2.20E+000}

13th _{8.09E-002 1.24E+001 5.12E+003 1.77E+003 3.90E+000}

19th _{1.09E-001 2.21E+001 6.24E+003 4.57E+003 5.00E+000}

25th _{4.47E-001 2.58E+001 8.23E+003 5.92E+003 6.17E+000}

Mean 2.84E-001 1.86E+001 8.07E+003 3.23E+003 4.44E+000

4

10

Std 2.99E-001 8.79E+000 5.07E+003 2.07E+003 1.96E+000

5

7th _{0.00E+000 5.68E-014 9.09E-013 1.13E-002 0.00E+000}

13th _{0.00E+000 5.68E-014 1.19E-012 7.22E-002 0.00E+000}

19th _{0.00E+000 5.68E-014 5.51E-012 2.99E-001 0.00E+000}

25th _{0.00E+000 5.68E-014 5.57E-012 5.17E-001 0.00E+000}

Mean 0.00E+000 5.68E-014 7.03E-012 3.54E-001 0.00E+000 Std 0.00E+000 2.32E-014 9.51E-012 5.21E-001 0.00E+000

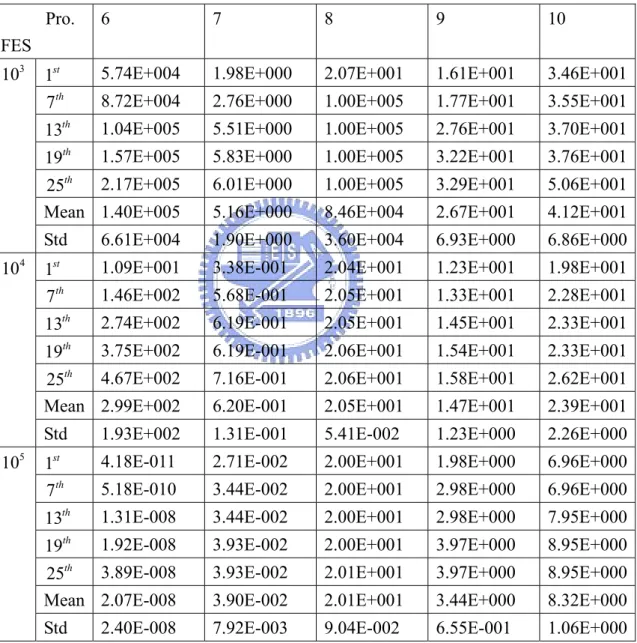
表 4.16 Dimension = 10，result of Function 6-10 Pro.

FES

6 7 8 9 10 1st 5.74E+004 1.98E+000 2.07E+001 1.61E+001 3.46E+001

7th _{8.72E+004 2.76E+000 1.00E+005 1.77E+001 3.55E+001}

13th _{1.04E+005 5.51E+000 1.00E+005 2.76E+001 3.70E+001}

19th _{1.57E+005 5.83E+000 1.00E+005 3.22E+001 3.76E+001}

25th _{2.17E+005 6.01E+000 1.00E+005 3.29E+001 5.06E+001}

Mean 1.40E+005 5.16E+000 8.46E+004 2.67E+001 4.12E+001

3

10

Std 6.61E+004 1.90E+000 3.60E+004 6.93E+000 6.86E+000 1st 1.09E+001 3.38E-001 2.04E+001 1.23E+001 1.98E+001

7th _{1.46E+002 5.68E-001 2.05E+001 1.33E+001 2.28E+001}

13th _{2.74E+002 6.19E-001 2.05E+001 1.45E+001 2.33E+001}

19th _{3.75E+002 6.19E-001 2.06E+001 1.54E+001 2.33E+001}

25th _{4.67E+002 7.16E-001 2.06E+001 1.58E+001 2.62E+001}

Mean 2.99E+002 6.20E-001 2.05E+001 1.47E+001 2.39E+001

4

10

Std 1.93E+002 1.31E-001 5.41E-002 1.23E+000 2.26E+000 1st 4.18E-011 2.71E-002 2.00E+001 1.98E+000 6.96E+000

7th _{5.18E-010 3.44E-002 2.00E+001 2.98E+000 6.96E+000}

13th _{1.31E-008 3.44E-002 2.00E+001 2.98E+000 7.95E+000}

19th _{1.92E-008 3.93E-002 2.00E+001 3.97E+000 8.95E+000}

25th _{3.89E-008 3.93E-002 2.01E+001 3.97E+000 8.95E+000}

Mean 2.07E-008 3.90E-002 2.01E+001 3.44E+000 8.32E+000

5

10

Std 2.40E-008 7.92E-003 9.04E-002 6.55E-001 1.06E+000

表 4.17 Dimension = 10，result of Function 11-15 Pro.

FES

1st 9.76E+000 2.73E+002 5.00E+000 3.87E+000 1.86E+002

7th _{1.01E+001 5.21E+002 6.66E+000 3.97E+000 2.61E+002}

13th _{1.04E+001 1.52E+003 6.86E+000 4.03E+000 3.59E+002}

19th _{1.05E+001 1.71E+003 7.03E+000 4.11E+000 3.83E+002}

25th _{1.15E+001 1.89E+003 7.64E+000 4.12E+000 4.03E+002}

Mean 1.06E+001 1.18E+003 7.03E+000 4.07E+000 3.30E+002

3

10

Std 6.48E-001 6.57E+002 9.81E-001 1.09E-001 8.23E+001 1st 4.82E+000 3.50E+001 4.70E+000 3.72E+000 1.82E+002

7th _{7.01E+000 5.27E+001 4.71E+000 3.75E+000 1.86E+002}

13th _{7.57E+000 9.80E+001 5.00E+000 3.77E+000 2.13E+002}

19th _{7.75E+000 1.07E+002 5.28E+000 3.77E+000 2.46E+002}

25th _{8.02E+000 1.15E+002 5.50E+000 3.81E+000 3.38E+002}

Mean 7.21E+000 8.17E+001 5.21E+000 3.78E+000 2.46E+002

4

10

Std 1.02E+000 3.18E+001 3.82E-001 4.38E-002 6.51E+001 1st 6.28E-001 5.97E-012 5.72E-001 2.59E+000 1.08E+002

7th _{1.44E+000 1.48E-010 5.74E-001 2.60E+000 1.16E+002}

13th _{2.43E+000 3.63E-010 5.80E-001 2.63E+000 1.43E+002}

19th _{3.01E+000 1.43E-009 6.29E-001 2.65E+000 1.56E+002}

25th _{3.08E+000 3.33E-009 6.74E-001 2.68E+000 1.68E+002}

Mean 2.24E+000 1.05E-009 6.40E-001 2.63E+000 1.42E+002

5

10

Std 9.25E-001 1.24E-009 6.38E-002 3.29E-002 2.57E+001

表 4.18 Dimension = 10，result of Function 16-20 Pro.

FES

16 17 18 19 20 1st 1.45E+002 4.38E+002 7.32E+002 8.27E+002 8.60E+002

7th _{1.81E+002 4.52E+002 8.40E+002 8.45E+002 9.82E+002}

13th _{1.86E+002 5.00E+002 9.31E+002 9.44E+002 1.00E+003}

19th _{1.87E+002 5.07E+002 1.00E+003 9.48E+002 1.04E+003}

25th _{1.91E+002 5.07E+002 1.01E+003 9.96E+002 1.04E+003}

Mean 1.83E+002 4.94E+002 9.38E+002 9.50E+002 1.00E+003

3

10

Std 1.38E+001 2.94E+001 1.02E+002 6.94E+001 5.50E+001 1st 1.30E+002 2.99E+002 3.88E+002 3.52E+002 3.98E+002

7th _{1.33E+002 3.22E+002 4.58E+002 4.84E+002 4.39E+002}

13th _{1.39E+002 3.24E+002 4.87E+002 5.36E+002 5.46E+002}

4

10

25th _{1.48E+002 3.42E+002 6.88E+002 6.36E+002 7.30E+002}

Mean 1.40E+002 3.38E+002 5.73E+002 5.87E+002 5.76E+002 Std 7.47E+000 2.10E+001 1.48E+002 1.22E+002 1.36E+002 1st 9.81E+001 1.62E+002 3.00E+002 3.00E+002 3.00E+002

7th _{1.02E+002 1.64E+002 3.00E+002 3.00E+002 3.00E+002}

13th _{1.04E+002 1.69E+002 3.00E+002 3.00E+002 3.00E+002}

19th _{1.06E+002 1.89E+002 3.00E+002 3.00E+002 3.00E+002}

25th _{1.09E+002 1.92E+002 3.00E+002 3.00E+002 3.56E+002}

Mean 1.04E+002 1.84E+002 3.00E+002 3.04E+002 3.19E+002

5

10

Std 3.66E+000 1.47E+001 0.00E+000 1.46E+001 3.16E+001

表 4.19 Dimension = 10，result of Function 21-25 Pro.

FES

21 22 23 24 25 1st 5.92E+002 8.13E+002 6.58E+002 2.94E+002 5.74E+004

7th _{7.43E+002 8.44E+002 1.07E+003 3.48E+002 8.72E+004}

13th _{1.07E+003 8.47E+002 1.29E+003 4.84E+002 1.04E+005}

19th _{1.23E+003 8.58E+002 1.30E+003 9.85E+002 1.57E+005}

25th _{1.28E+003 8.58E+002 1.32E+003 9.98E+002 2.17E+005}

Mean 1.05E+003 8.65E+002 1.22E+003 7.48E+002 1.40E+005

3

10

Std 2.49E+002 3.01E+001 1.86E+002 3.31E+002 6.61E+004 1st 5.00E+002 7.95E+002 5.59E+002 2.01E+002 1.09E+001

7th _{5.01E+002 8.02E+002 5.83E+002 2.01E+002 1.46E+002}

13th _{5.02E+002 8.04E+002 6.26E+002 9.53E+002 2.74E+002}

19th _{5.04E+002 8.06E+002 6.43E+002 9.56E+002 3.75E+002}

25th _{1.04E+003 8.08E+002 1.00E+005 9.63E+002 4.67E+002}

Mean 1.48E+004 8.07E+002 3.37E+004 7.07E+002 2.99E+002

4

10

Std 3.47E+004 6.18E+000 4.68E+004 3.57E+002 1.93E+002 1st 5.00E+002 7.32E+002 5.59E+002 2.00E+002 4.18E-011

7th _{5.00E+002 7.32E+002 5.59E+002 2.00E+002 5.18E-010}

13th _{5.00E+002 7.53E+002 5.59E+002 2.00E+002 1.31E-008}

19th _{5.00E+002 7.54E+002 5.59E+002 2.00E+002 1.92E-008}

25th _{5.00E+002 7.56E+002 5.59E+002 2.00E+002 3.89E-008}

Mean 5.16E+002 7.46E+002 5.59E+002 3.24E+002 2.07E-008

5

10

表 4.20 Dimension = 30，Result of Function 1-5 Pro.

FES

1 2 3 4 5 1st 1.45e+004 4.79e+004 4.05e+005 9.13e+004 1.79e+004

7th _{1.85e+004 5.85e+004 1.23e+006 1.97e+005 1.99e+004}

13th _{2.09e+004 6.87e+004 1.48e+006 2.39e+005 2.11e+004}

19th _{2.51e+004 7.16e+004 1.86e+006 3.58e+005 2.27e+004}

25th _{2.82e+004 8.22e+004 2.29e+006 4.63e+005 2.49e+004}

Mean 2.37e+004 7.38e+004 1.70e+006 3.12e+005 2.24e+004

3

10

Std 6.11e+003 1.33e+004 5.60e+005 1.28e+005 2.81e+003 1st 1.22e+003 1.65e+004 2.32e+005 8.40e+004 7.04e+003

7th _{1.56e+003 2.97e+004 3.38e+005 1.13e+005 9.24e+003}

13th _{2.18e+003 3.46e+004 4.13e+005 1.37e+005 1.08e+004}

19th _{2.62e+003 3.68e+004 4.68e+005 1.47e+005 1.16e+004}

25th _{3.04e+003 3.76e+004 5.27e+005 1.70e+005 1.30e+004}

Mean 2.45e+003 3.52e+004 4.37e+005 1.42e+005 1.09e+004

4

10

Std 8.59e+002 7.16e+003 1.20e+005 3.52e+004 2.00e+003 1st _{9.66e-013 4.03e-001 1.35e+002 2.73e+004 4.24e+002}

7th _{1.45e-011 5.86e+000 4.29e+002 4.96e+004 1.42e+003}

13th _{2.79e-011 2.20e+001 8.03e+002 5.78e+004 1.83e+003}

19th _{5.65e-011 4.12e+001 1.39e+003 6.68e+004 2.71e+003}

25th _{1.42e-010 6.31e+001 4.55e+003 7.75e+004 4.00e+003}

Mean 8.81e-011 6.03e+001 4.35e+003 6.18e+004 2.42e+003

5

10

Std 1.15e-010 5.97e+001 9.44e+003 1.47e+004 1.43e+003 1st 5.68e-014 3.66e-008 4.35e-003 2.12e+004 8.17e+001

7th _{5.68e-014 2.25e-007 8.56e-002 2.55e+004 1.17e+003}

13th _{1.13e-013 2.80e-007 2.08e-001 3.17e+004 1.33e+003}

19th _{1.13e-013 3.81e-007 5.81e-001 3.62e+004 2.22e+003}

25th _{1.13e-013 5.60e-007 1.35e+000 3.99e+004 3.17e+003}

Mean 1.06e-013 4.42e-007 5.82e-001 3.36e+004 1.93e+003

5

3 10×

Std 3.70e-014 2.12e-007 6.16e-001 8.58e+003 1.33e+003

表 4.21 Dimension = 30，Result of Function 6-10 Pro.

FES

6 7 8 9 10

3