ON MINIMUM CRITICALLY N-EDGE-CONNECTED GRAPHS

ON MINIMUM CRITICALLY

n-EDGE-CONNECTED

GRAPHS* MARGARET B.

_COZZENS

AND SHU-SHIH Y. _WUf:l:

Abstract. Letn bean integerwith n> 2. A graph Giscalled criticallyn-edge-connectedifthe edge-connectivityMG) n and forany vertexv ofG, ,(G v) n 1.Thesizesof critically n-edge-connected graphsareimportant and interestingin applications in communicationnetworks.The maximumgraphswith thisproperty have beencharacterized[2]. Inthis paper, we first discuss some propertiesofminimumgraphs, thenshowthattheproblem of findingaminimum critically n-edge-connected spanning subgraph ofagiven graphGis NP-complete.

Keywords, graph theory, edge-connectivityX(G),connectivityK(G),NP-completeness

AMS(MOS)subject classification. 05C41

1. Introduction. Letn be afixed integer with n

>=

2. Agraph G shall be called

n-edge-connectedifthe edge-connectivity k(G) n. AgraphG iscalledcritically

n-edge-connectedifGisn-edge-connectedandforany vertexv of

G,

k(G v) n 1.Agraph

Giscalledn-connectedif the vertexconnectivity,r(G) n.AgraphGiscalled critically

n-connectedifGisn-connectedandfor anyvertexvin

G,

r(G v) n 1.Agraph G

is a minimum (maximum) critically n-edge-connected graph if no critically

n-edge-connectedgraphswiththesame number of verticeshasfewer(more)edges than G. In acommunication networkand circuitdesign, reliabilityisoftendeterminedby the connectivity and edge-connectivity of the corresponding graph. Thereforeit is

im-portantto investigate, for fixed n, criticallyn-connectedgraphs([3], [7]), andcritically

n-edge-connected graphs. We characterizedthe maximum graphs in a subset of

criti-cally n-edge-connected graphs, for each n

>=

2 in[2]. Hereweinvestigatetheminimum

critically n-edge-connected graphs.

Weuse

{x}

todenote the least integer greaterthan orequaltox,and

[x]

the greatest integer less than orequaltox.

2. Anexample of a minimum criticallyn-edge-connected graph. Foranyfixed

in-tegersn, m,m>_-n

+

1,Harary [5]constructedclasses ofgraphs

H,,,m,

thatareminimum n-connected. These same graphs are minimum critically n-edge-connected graphwith

order m.

H,,,m

isconstructedasfollows:

Case 1. n iseven. Let n 2r. Then

H2r,

hasvertices0, 1, 2, 3, m and

twovertices andj areadjacent if r

=<

j_-<

+

r(whereaddition istakenmodulom).

H4,8

isshowninFig. 1.

Case 2. n is odd (n > 1), m is even. Let n 2r

+

(r > 0). Then H2r/

,,

is

constructed by first drawing

H:r,m,

and then adding edges joining vertex to vertex

+

m/2

for

=<

< m/2.

H5,8

isshown in Fig. 2.

Case 3. n is odd (n> 1), m is odd. Let n=2r+

(r>0).

Then

H:zr+,m

is constructed by first drawing

H2r,

and then adding edges [0, (m- 1)/2] and

[0,(m

+

1)/2],and[i,

+

(m

+

1)/2] for <- _{< (m 1)/2.}

_H5,9

is shownin Fig. 3.

In Case and Case 2,

degHn,m(i)

n, for all

V(H,,,m)

so that

IE(Hn,m)l

1/2

i

V(Hn,m)

degHn,m(i)

1/2

n"m.

Receivedby the editors October 1, 1986; accepted forpublication(inrevisedform)April30, 1987. fDepartmentof Mathematics, Northeastern University,Boston,Massachusetts02115.

t

DepartmentofAppliedMathematics,National ChiaoTungUniversity, Hsinchu, Taiwan, Republic of China.

659

660 M. B. COZZENS AND S.-S. Y. WU 7 6 2

H4,8:

FIG. 7

H5

8:

6 FIG.2 5 4 FIG.3

In Case 3,

_degn.,(i)

n, for 1,2, m 1, and

degn.,(0)

n

+

1. Sothat

ZVtZ.,m)

degn.,m(i)

=nm

+

_2"IEI.

So

IE(H.,m)I

=(nm

+

1)/2.

Therefore for any fixed integers n, m, rn >_-n

+

1,

E(Hn,m)l

{nm/2}.

Nowwe show that

H.,m

isa minimum critically n-edge-connected graph, i(G) is

theleast degree overallverticesofG.

THEORZM 1. The graph

Hn,m

isn-connected [5].

Fromthe construction of

Hn,m,

it isclearthat

6(H.,m)

n, andsince

n

<=

K(Hn,m)

<-

_,(Hn,m)

<-

_6(Hn,m)

_n,

wehave

X(Hn,m)

6(Hn,m)

n.Therefore,we have the following theorem.

THEOREM2. Thegraph

Hn,m

isn-edge-connected.

Forverticesjandkin agraphG,a(j,

k)-cutset

ofGis a vertex cutset Tsuchthat

jandkare indifferent componentsofG T.

THEOREM3. The graph

Hn,m

{

i}

is(n 1)-connected,

for

anyvertex in

H,,m.

Proof

Let n=2r if n is even, 2r+ if n is odd. The minimum degree,

6(Hn,m

{i}),

isn so there existsa vertexcutset ofsize n 1. We will show that there is novertexcutsetwithfewer than n vertices.

Suppose there existsa vertex cutset Tsuch that 2 -<

TI

< n 1. Letjandkbe

vertices belongingtodifferentcomponents of

_(H,,m

_{

i})

Tsuchthat if isbetween

jandkthen0

=<

k < <j,and if isnotbetweenjand k thenj< k.Define two vertex

setsA andBin

_Hn,m

_{

_i}

_(additionismodulom):

A={j,j+I,j+2,

,k-l,k},

B

{k,k/

1,k+2,---,i- 1,i+ 1,.-. ,j-

1,j}.

Note thatA U B

V(Hn,m

{i})

andA f) B {j,

k}.

Since

ITI

< n 1,

ITI

< 2r.

Therefore notboth Tf’lAand T N Bcan haver ormoreelements.

Case 1.

IT

f’l

AI

< r. A T A (A Cl T) so no more than r consecutive

elements are removed fromA by T. Hence A Thas a sequence ofdistinct vertices startingwith jand endingwithkwith nodifference greater than rbetween any pair of

consecutive vertices. This sequence is a (j, k)-pathin

_(H,,m

_{

_i})

T,

acontradiction

to

T

beinga(j,

k)-cutset.

Case2.

IT

BI

<r.

Subcase (i).

_IT

fq_{B < r- 1.Asin Case 1, no} more than r- 2 consecutive

elements are removed from Bby T. Hence B Thas a sequence of distinct vertices

startingwithkandendingwith j,and the difference between anytwo consecutivevertices

isat most(r 1)

+

r.(Thereis anadditional inthegap between and

+

1.)

This sequence is a(k,j)-path of

(Hn,m

{

i})

T,

acontradiction to Tbeing a (j,

k)-cutset.

Subcase (ii).

IT

B r 1.Since jand karenotin

T,

ITf3AI=ITI-ITf3BI<n

1-(r-1)=n-r<r+ 1.

If

_IT

fq

AI

_{< rthen Case} applies. Therefore

IT AI

r.

IAI

+

IBI

(m

+

2)

m

+

1. Thereforenotboth of

IAI

and

[B[

canbe greater than

{(m

+

1)/2},

butatleast

oneis greater thanorequalto

_{(m

₊

1)/2

}.

Suppose

_AI

>--

{(m

+

1)/2

}.

If there existsa sequenceof verticesinA Tbeginning

withj and ending with k such that no pair of consecutive terms has a difference >-r

+

1, then thissequenceisa (j,k)-pathin

(H,,m

{

i})

T,

acontradiction toTbeing

662 M. B. COZZENS AND S.-S. Y. WU

a(j,

k)-cutset.

Thuswemayassumethat every sequence ofverticesinA Tbeginning withjand endingwithkhasapairofconsecutive terms with difference

>=

r

₊

1.In fact,

since

_IT

N

_AI

r, this difference is exactlyr

+

1,and thereisonlyonesuchconsecutive

pair with differencer

+

1.All other consecutivepairshaveadifferenceof1.Callthepair

of vertices with difference r

+

1, sand s

+

r

+

inthe sequenceA T. Thuswe can

writeA-Tas{j,j+

1,j+2,.-.,s- 1,

s,s+r+

1,-..,k- 1,

k}

(Notethat j can

bes.)SplitA Tinto two parts:

A=(j,j+l,...,s-l,s}

and

A2 ={s+r+l,s+r+2,...,k-l,k}.

The differencein consecutive terms in each

_Ai

is 1,sothere is anedgein

(Hn,m

{

i})

Tbetween them. But m >_- n

+

>=

2r

+

implies m/2 >- r

+ 1/2

> rif m iseven, and

(m

+

1)/2

>=

r

+

>

rif m isodd. Thusthere are some

_a

A and

a

A2

such that

a2

a

+

[(m

+

1)/2]. The sequence

{j,

j/ 1, a, a2, k- 1,

k)

is a (j,

k)-path in

(H,,m

{

i})

T,

a contradiction to Tbeinga (j,

k)-cutset.

If

BI

>=

{(m

+

1)/2

}

thenthesameargumentapplies sincen >

TI

->-

2 implies

n >_- 4,hencer>_- 2,sothereis anedge between and

+

in

_H,,m

_{

_i}.

All that remains is to show that no vertex cutset of only one vertex exists for

H,,m

{i}.

Suppose T=

{p}

isa vertex cutset

ofH,,m

{i}.

Since

IT]

< n 1, n

>=

3.

Casel. Ifp=i- l(equivalentlyi=p+ 1),theni+ 1, i+2,...,m- 1,0,.-.,

2is apath containing all the vertices of

H,,m

{

i,

p},

acontradiction to Tbeinga

cutsetof

H,,m

{

i}.

Case 2. p 4 andp 4

₊

1. Without loss of generality assume < p

=<

m- 1.

NowP

=p+

1, p+2,.-.,m- 1,0, 1,.-.,i- lisapathandP2=i+ 1,

+

2, p is apathin

_(H,,m

_{i})

{p}.

Ifniseventhen r

>=

2 and

{i-

1,i+

l}.E(Hn,m)

sothere is only one component of

(H,,m

{

i})

{p}.

Ifn isodd then there existsan

edgebetweensomexin

_P

andx

+

[(m

+

1)/2]inP2, again contradictingT

{

p}

being

a cutsetof

H,,m

{

i}.

Therefore, thereexists no cutset with only one vertex, andthe

theorem is proved.

QED

Since n _-<

(Hn,m-

{i})

=<

X(Hn,m

{i})

=<

6(Hn,m

{i})

n 1, we have

(Hn,m

{

i})

6(Hn,m

{

i})

n 1. Therefore,wehavethefollowing theorem.

THEOreM 4. The graph

Hn,m

{i}

is (n 1)-edge-connected,

_for

any vertex

in

H,,m.

Now

we canshow themaintheorem ofthissection.

THEOREM5. Forany given positive integersm,n,m>-n

+

1,thereexistsa minimum

criticallyn-edge-connected graph withorderm.

Proof

By Theorem 2 and Theorem 4,

Hn,m

is critically n-edge-connected.

IE(Hn,m)[

{nm/2}

and

_IV(H,,,m)I

m.

Let

G (V,E) be a critically n-edge-connected graph with

_VI

m. Thus

,(G) n, and for anyvertexvin

G,

X(G)

=<

6(G)

=<

degGv. Hence

2"IEI

veV(G)

degGv

>=

m.6(G) m.n.

So

_IEI

-> _mn/2.

_IEI

is an integer, hence

IEI

>=

{mn/2}

[E(nn,m)l.

So no critically n-edge-connected graph with m verticeshasfewer edgesthan

H,,,m.

Therefore

H,,,m

isa

minimum critically n-edge-connected graphwithorderm.

QED

a a 2 a3 G-

al

a5

a1

a 7

al

2

al

a6

FIG. 4

3. Characterizations of minimum critically n-edge-connected graphs. In addition

to

Hn,m,

there are other minimumcritically n-edge-connected graphs. First we discuss

somepropertiesof minimum critically n-edge-connected graphs.

Fromthediscussionof the graph

Hn,m,

it iseasytoobtainthe followinglemma.

LEMMA

6.

_If

Gisa minimumcriticallyn-edge-connectedgraph withorderm, then

IE(G)I-

{mn/2}.

AgraphGiscalledalmostregular

_of

degreen ifthereis at most one vertexof degree n

+

and all other vertices have degreen.Clearly,an n-regular graphisalmost regular of degree n.

THEOREM7.

_If

G

V,

E) isa minimum criticallyn-edge-connectedgraph, then

Gisalmost regular

_of

degreen. Theproof

follows from

Lemma 6.

The converse ofTheorem 7is not true. G,asshownin Fig. 4,isalmostregularof degree 5, but G is not critically 5-edge-connected, since k(G) 5, and k(G a0)

34:5- 1.

IfG is n-edge-connected, then the order ofG, m, is such that m >- n

+

1. For

n

+

=<

m

=<

2n, we havea characterization of minimum critically n-edge-connected graphs.

THEOREM 8. Let the order

_of

G be m. For any n such that n

+

<=

m

<=

2n,

G (V, E) is a minimum critically n-edge-connected graph

_if

andonly

_if

Gis almost

regular

_of

degreen.

To

prove Theorem 8,we willusethefollowing lemma.

LEMMA

9.

_If

G hasm verticesand 6(G)

>=

[m/2], then

X(G)

6(G) [1 ].

Proof

of

Theorem8. ByTheorem 7,ifGis a minimumcritically n-edge-connected graph, then Gisalmost regularof degree n.

Conversely, ifGisalmost regular of degree n, then 6(G) n

>=

m/2

>=

[m/2]. By

Lemma 9, we have (G) 6(G) n. Forany vertex u V(G), 6(G u) n

>=

m/2- 1. Since n- is aninteger,n- >_-

{m/2-

}.

Case 1. rn isodd.

6(G-u)=n

-1=> n-l=

>-m+2 1==2-1

2-1

Case2. rniseven.

6(G-u)=n-

>=

_-1

m-2

664 M. B. COZZENS AND S.-S. Y. WU ByLemma9,wehave X(G u) 6(G- u) n 1.

IE(G)I

---

degav veV(G) mn

--,

or

((m-

1)n

+n+

1)

_=(mn+

1)

Therefore, Gisaminimumcritically n-edge-connected graph. QED

The reader shouldnotethatGneednot be n-connectedinTheorem 8.

Ingeneral, the converse of Theorem 7 is nottrue, but ifthe vertex connectivity

K(G) n,then wecan giveacharacterization ofminimum critically n-edge-connected

graphs.

THEOREM 10. Let K(G) n.G (V,E)isa minimumcriticallyn-edge-connected

graph

_if

and only

_if

Gisalmost regular

of

degreen.

Proof

LettheorderofGbem. ByTheorem7,weobtainthe "onlyifpart."

Conversely, ifG isalmost regular of degree n, then 6(G) n. Since n (G) -<

X(G)

_-<

6(G)

n,wehaveX(G) n.

Forany vertex uin

G,

(G u)

=<

X(G u)

=<

6(G u) n 1. Suppose that

X(G u) < 6(G u), for some vertex u in G, then (G u) -< _{X(G u) < n} 1.

Thus, the connectivity (G) < n, a contradiction. So for any vertex u in G, we have

X(G- u) 6(G- u)= n- 1.

Gisalmostregular of degree n,sobytheproof of Theorem 8,

IE(G)[

{ran

Therefore, Gis a minimumcritically n-edge-connected graph. QED

The condition K(G) n in Theorem 10 isnecessary, sincewe can find agraph

G,

the one shown in Fig. 4, which is almost regular of degree n with (G) < n, G is a

minimum n-edge-connected graph, but G is not critical with respect to X(G). Here

(G) 4,since

{a2,

a9, al0,all

}

is a vertex cutset.

Form>_- 2n

+

1,we cangivesomecharacterizationsof minimum critically n-edge-connected graphs.

THEOREM 1. Foranygiven positive integersm, n,m >- 2n

+

1,and

lV(G)l

m,

G (V, E) isa minimum critically n-edge-connected graph

_if

and only

_if

Gis almost

regular

_of

degree n, and

_for

each vertex u in a vertex cutset T with

TI

-<n- 1,

X(G- u) >_- n- 1.

Proof

ByTheorem 7, ifGis a minimum critically n-edge-connected graph, then

Gisalmost regularof degree n.Since Gis critical with respect to X(G), for eachvertex

uin

G,

X(G u) n 1.So"theonlyifpart"iscomplete.

Conversely, ifG is almost regular of degree n, then 6(G) n. Since X(G u)

>_-n- forsome vertexuin

G,

andi(G) n,wehaveX(G)>_- _n 1.

Suppose X(G) n 1.Let

El

beaminimumedge-cutsetand

G,

G2

betwo

com-ponentsofG

_E.

6(G) n and

_IEll

n 1, so

IV(G)I

>- _{2 and}

_[V(G)I

_{>_- 2.} Since

rn >- 2n

+

1, withoutlossof generality, wemaylet

V(G)I

>=

n

+

1.Let Abethe setof verticesin

_G1

which are incident with

_El.

IAI

-< n 1, since

[Eli

n 1. SoA is a

vertexcutset with

IAI

=<

n 1,andfor anyvertexuinA, X(G u)

=<

n 2,acontradiction.

Therefore ,(G) > n 1. n < X(G)

=<

6(G) n, so X(G) n.Therefore G is

n-edge-connected. Weshow nextthatGiscritically n-edge-connected.

Foreach vertex u in

G,

we consider the followingtwo cases fora cutset

contain-ing it.

Case 1. u isin a vertex cutset Twith

IT[

=<

n 1, then ?(G u) -> n 1. Since

,(G-u)<=b(G-u)=n- 1,wehaveX(G-u)=n- 1.

Case 2. Every vertex cutset containing u has at least n vertices. Suppose

X(G

u)

< n 1.

Let/

be a minimum edge-cutset of G u, and

H,

H2

be two

componentsof(G u)

-/.

V(H)I

+

[v(n2)l

m >_- (2n

+

1) 2n.Without

lossof generality, let

V(H)I

>=

n.Since

I?1

<n 1, umustbe adjacenttosomevertices

in

_H

andsome vertices inH2, asshown inFig. 5.

Let

_T

betheset ofvertices in

_H

which are incident

with/.

T[

< n 1, since

I/l

<n 1.

[V(H)

Z[

> 1.Thus

_T

LI

{u}

is a vertex cutsetofG and

]T

tA

{u}]

_-< n 1, a contradiction to the assumption ofthis case. So X(G u) >_- n 1. Since

X(G u) _-< 6(G u) n 1,we have X(G u) n 1. Therefore Giscriticalwith

respect to X(G).

Gisalmostregular of degree n, by the proof of Theorem 8,

IE(G)[

{ran

where

misthe orderofG. Therefore, Gis a minimum critically n-edge-connected graphwith

orderm.

QED

A vertex u ofa graph G is called criticalifu is contained in a minimum vertex

cutset. Thus,wehavethe followinglemma.

LEMMA 12. A vertexu ingraphG iscritical

_if

andonly

_if

(G u)

(G)

1.

COROLLARY

13. For any given positive integers m, n, such that rn >-_ 2n

+

1,

IV(G)[

m, and

(G)

>=

n 1, G (V, E) isa minimum criticallyn-edge-connected graph

_if

and only

_if

G is almost regular

_of

degree n, and

_for

any critical vertex u,

X(G-u)>_-n- 1.

Next,

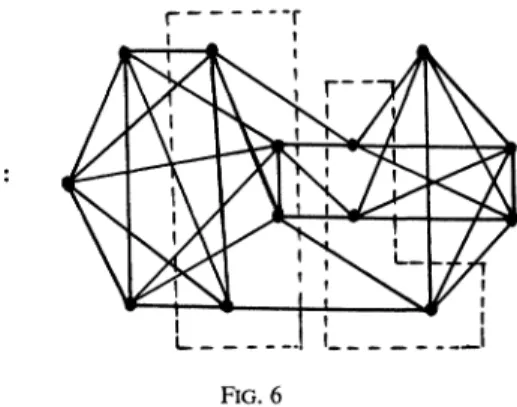
wegivesomeexamplesto illustrateTheorem 11 andCorollary 13. Example 1. Gisshownin Fig. 6.

Gisalmostregular of degree5,(G) 3.Foranyvertexu in a vertex cutset Twith

IT[

_-< 4, X(G u) >_- 4. By Theorem 11, Gis a minimum critically 5-edge-connected graph.

Example 2. Gisshown inFig. 7.

Gisalmostregular of degree5, (G) 4, and for anycritical vertexu, X(G u)

>=

4. ByCorollary 13, Gis aminimum critically5-edge-connected graph.

Example3. GisshowninFig. 8.

HI

u

H2

G"

FIG. 5 FIG. 6

666 M. B. COZZENS AND S.-S. Y. WU

FG. 7

G is almost regular of degree 5, K(G)= 3, u is in a vertex cutset

S,

[SI

4,

k(G

u)

3 <5 1.ByTheorem 11 Gis not a minimumcritically 5-edge-connected graph.In fact, Gis notcritical withrespecttok(G).

Example 4. Gisshown in Fig. 9.

Gis almost regular of degree 5, K(G) 4, uis a critical vertex, but k(G u)

3 < 5 1. ByCorollary 13, Gis not a minimumcritically 5-edge-connected graph. In

fact, Gis notcritical withrespect to k(G).

COROLLARY

14. Forpositive integersm, n, m >- 2n

+

1, at leastone

_of

n or m is

even, and

IV(G)]

m, G (V, E) is a minimum criticallyn-edge-connected graph

_if

and only

_if

G is regular

_of

degree n, and

_for

any vertex u in a vertex cutset T with

IT]=<n-

1,(G-u)

->n-

1.

Proof

ByTheorem 11, Gis a minimum critically n-edge-connected graphifand

only ifGisalmost regular ofdegree n, andfor anyvertex u in a vertex cutset Twith

[Tl=<n-

1,

X(G-u)>-n-

1.

Now, supposethatGis notregular of degree n, butGisalmostregular of degreen.

Then vt) degav n(m 1)

+

(n

+

1) nm

+

is odd, since nm is even. But

Zo

vt)degv

2.

IEI,

so weobtainacontradiction.Conversely,ifGisregularof degree n, then Gisalmost regular of degree n. QED

4. NP-completeness. Aproblem isinthe classNPif some nondeterministic machine

could,inevery instance, find the answer inanumber ofsteps which isbounded by some

fixed polynomial in the length of the inputdata. A problemis NP-complete ifit is in

NP,

and the existence ofadeterministic polynomial algorithm, foritwould imply the

FIG.8

FIG.9

existenceofadeterministic polynomial algorithm for allNPproblems. Theproof

tech-nique for NP-completeness in thissection usesthe restriction technique. An

NP-com-pleteness proof by restriction for agiven problem

Q

e NP consists simply ofshowing

that

Q

containsaknown NP-complete problemRas a special case.

Themain problem in this sectionis asfollows:

Problemn-EDGE.

Instance:

G (V,E),a positiveintegern, < n _-<

IV[

1.

Question: Isthere a minimum critically n-edge-connected subgraph G’ (V, E’)

ofG?

Weshall showthat Problem n-EDGEisNP-complete. Todo this, we willuse the NP-completeproblem, the Hamiltonian CircuitProblem (HC).

Problem HC.

Instance:

Graph G (V, E).

Question: Does Gcontain a Hamiltoniancircuit?

LEMMA

15. G’

V,

E’) isaconnectedspanningsubgraph

_of

G

V,

E) and G’

isalmost regular

of

degree2

_if

and only

_if

G’isaHamiltoniancircuit

of

G.

Lemma

15 isprovedby usingthe factsthat the number ofverticesofodddegree for any graphiseven,aconnected graphwith no verticesof odd degreeisEulerian, and

anEulerian circuitin a 2-regular graphmust be aHamiltoniancircuit.

There are many polynomial time algorithms for computing the number of

com-ponentsofagraph G (V, E)including theonegivenin[8].

Nowwe considerProblemARn. Problem ARn.

Instance: G (V, E),a positiveintegern, < n_-<

IV[

1.

Question: Isthere a spanning connected subgraph G’ (V, E’), such that G’is almostregular of degreen?

THEOREM 16. ProblemARn isNP-complete.

Proof

First, we prove that Problem ARn is in NP: Given a yes solution (called

certificate)toProblem

ARn,

wegiveapolynomial checking algorithm:

Certificate: asubgraph G’ofG.

CERTIFICATE-CHECKING ALGORITHM

(Procedure

I):

Begin

1. If

V(G’)

4: V(G)

Thenreturn"No"

Else

2. Ifc(G’) (thenumberofcomponentsof

G’)

>=

2

Thenreturn"No"

Else

668 M. B. COZZENS AND S.-S. Y. WU

End.

Sortdegrees ofvertices in

G’,

suchthat

d

<=d_<=d3

<=

<=d,;

If(dl=

d2

d3

dm-

n)and (d, n ord, n

+

1)

Thenreturn

"Yes"

Else return

"No";

Step 2 isapolynomial procedure. Step 3 is asorting procedure, so it also runs in

polynomial time.Therefore,the certificate-checking algorithmrunsinpolynomialtime, Problem

ARn

isinNP.

Letn 2.Problem ARnisreducedtoProblem HCby Lemma 15. Soa specified type of instance of Problem

ARn

is NP-complete.Bythe "restriction technique,"Problem

ARn

isNP-complete.

QED

Problemn-EDGE-T.

Instance:

G (V,E),a positiveintegern, <

Ivl/2

--<

n _-<

[Vl

1.

Question: Isthere aminimum critically n-edge-connected subgraph G’ (V, E’)

ofG?

THEOREM 17. Problem n-EDGE-TisNP-complete.

Proof

ByTheorem8,Problemn-EDGE-Tisthesame asProblemARn. SoProblem

n-EDGE-TisNP-complete.

QED

Problem MENS(Minimum n-edge-connected subgraph).

Instance: G (V,E)andpositiveintegersn _-<

VI

andb

=<

_EI.

Question: Isthere asubset

E’

_

Ewith

E’I

-< b such thatG’ (V,E’)is n-edge-connected?

COROLLARY 18. Problem MENSisNP-complete[4].

Therefore,ifG’ (V,

E’)

is acertificate,thenthereis apolynomialtime

certificate-checking algorithm for Problem

MENS,

wecallit"Procedure

II."

THEOREM 19. Problem n-EDGE isNP-complete.

Proof

First, weshow that Problemn-EDGE is inNP.

Certificate:AsubgraphG’ofG.

CERTIFICATE-CHECKINGALGORITHM:

Begin

1. IfG’isnot aspanningconnectedsubgraph ofGorG’is notalmost regular of

degreen--(CallProcedureI)

Then return

"No"

Else

2. IfG’is notn-edge-connected--(Call ProcedureII)

Then return "No"

Else

3. For I :=

Construct

H’

G’-

v,

H G- vi;

If

H’

isnot(n 1)-edge-connected--(Call ProcedureII (Instance:

H,n-

1))

Thenreturn "No"andgo to5.

Else gotoloop3;

Return

"Yes";

End.

Instep 1, ProcedureIrunsinpolynomial time

_P.

Instep2,ProcedureIIruns inpolynomialtime

_P2.

Instep3, the number ofcomputation stepsisO(P2"

Therefore, the certificate-checking algorithm runs in polynomial time, Problem

n-EDGEisNP.

Ifwe useinstancen,

vI/2

--<

n

=<

vl

1, Theorem17and the "restrictiontechnique,"

Problemn-EDGE is NP-complete. QED

Wehave shown that the problem of findingaminimumcritically n-edge-connected spanningsubgraph ofGis NP-complete. Ifweplace any restrictions ongraph G other than theonesimposedin Theorems8, 10, 11andCorollary 13 does the problem become easier?

Wethank the referee ofanearlierversion of thispaperforhishelpful suggestions.

REFERENCES

G.CHARTRAND, Agraph-theoretic approachto acommunicationproblem,SIAMJ.Appl.Math.,14(1966),

pp.778-781.

[2] M. I. COZZENSANDS.-S. Y.Wu,Maximumcriticallyn-edge-connected graphs,J.Graph Theory, submitted. [3] R. C. ENTRINGER,Characterizationofmaximumcritically 2-connectedgraphs, J.Graph Theory, 2(1978),

pp.319-327.

[4] M. R.GAREYANDD. S. JOHNSON,Computer and Intractability:AGuidetothe TheoryofNP-Completeness, W. H. Freeman, SanFrancisco, 1978.

[5] F. HARARY, Themaximumconnectivityofagraph,Proc. Nat.Acad. Sci. U.S.A.,48(1962),pp. 1142-1146.

[6]

.,

GraphTheory, Addison-Wesley, Reading,MA, 1969.

[7] n.J.I(ROLANDH.J.VELDMAN, Onmaximumcriticallyh-connected graphs,DiscreteMath.,52(1984),

pp.225-234.

[8] C.

n.

PAPADIMITRIOUANDK. STEIGLITZ,CombinatorialOptimization,Algorithms and Complexity, Pren-tice-Hall, Englewood Cliffs,NJ, 1982.