Optimal and Heuristic Algorithms for the Power-Based QoS Multiple Routing Problem for Mobile Ad Hoc Networks

(1)

Optimal and Heuristic Algorithms for the Power-Based QoS

Multiple Routing Problem for Mobile Ad Hoc Networks*

Pi-Rong Sheu Chia-Hung Chien Wei-Sheng Liao Yu-Ting Li Zhi-Cheng Chen

Department of Electrical Engineering

National Yunlin University of Science & Technology

Touliu, Yunlin 640, Taiwan, R.O.C.

Email:

sheupr@yuntech.edu.tw

Abstract

In this paper, we will consider the problem of searching for multiple paths between multiple pairs of sources and destinations satisfying the power requirement in a mobile ad hoc network. The problem has been proved to be an NP-complete problem. In this paper, according to the principle of network flow and linear programming techniques, we will propose an integer linear programming formula to generate the optimal solution for this problem. Furthermore, based on the Dijkstra’s algorithm, efficient heuristic algorithms with low time complexities are developed. Computer simulations verify that the suboptimal solutions generated by our heuristic algorithms are very close to the optimal ones.

Keywords: Ad Hoc Network, Multiple Routing, Power-Aware, Routing, Quality of Service

摘要

在本篇論文中，我們將要探討如何為隨意網路之多個來源節點找尋多條路徑來將它們的資料封包繞送到它們各自的目的節點並且保證在整個資料封包的繞送過程中都不會發生電力不足的情況。這個問題已經被証明是一個 NP-complete 問題。在本篇論文中，根據網路流量的原理和線性規劃的技巧，我們將提出一個整數線性規劃公式來求解這個問題的最佳解。此外，基於 Dijkstra’s 演算法的技巧，我們也將提出擁有較低時間複雜度的發式演算法來求解這個問題的次佳解。電腦模擬結果顯示我們的發式演算法所求得的次佳解是相當接近最佳解的。關鍵字: 隨意網路，多重路徑繞送，電力考量，路徑繞送，服務品質

1. Introduction

The research of mobile ad-hoc network (MANETs) has attracted a lot of attentions recently. In particular, since MANETs are characterized by their fast changing topologies, extensive research efforts --- *This work was supported in part by the National Science Council of the Republic of China under Grant # NSC 93-2213-E-224-023.

have been devoted to the design of routing protocols for MANETs. Furthermore, since the operation of MANET mainly relies on battery power, power consumption becomes an important issue [3, 4, 6]. Several power-aware routing protocols have been proposed. Most of the existing power-aware routing protocols are designed primarily either to evenly distribute packet-relaying loads to each mobile host to prevent the battery power of any host from being overused or to minimize the total power consumption of the entire network. Little attention is paid to the issues related to the power-based quality-of-service (QoS) requirement of a route, i.e., to provide guaranteed battery power for the transmission of packets along a path from a source to a destination such that any host in the path does not run out of its power during the transmission of packets. Only recently have people turned their attentions to establishing routes with QoS given in terms of power. In [7], the authors have proposed a power-based QoS unicast routing algorithm for MANETs. It can guarantee the transmission of a given amount of packets along a single path in the MANET to be supported by the residual power capacity of each node along the path.

In a realistic MANET, it is a more common situation that multiple sessions are in progress at the same time. That is, a lot of sources want to communicate with their individual destinations simultaneously. In this paper, we will consider the problem that given multiple pairs of sources and destinations in a MANET, find a route between each pair of source and destination satisfying the power requirements, namely, guaranteeing that the transmission of data packets during a session can be supported by the residual power capacity of each node along the route. The problem is named as the

power-based QoS multiple routing (PQMR) problem.

The PQMR problem is first defined and discussed in [5] and has been proved to be an NP-complete problem [5].

In this paper, according to the principle of network flow and linear programming techniques [1], we will propose an integer linear programming (ILP) formula to generate the optimal solution for the PQMR problem. Furthermore, based on the Dijkstra’s

(2)

algorithm, efficient heuristic algorithms with low time complexities are developed. Computer simulations verify that the suboptimal solutions generated by our heuristic algorithms are very close to the optimal ones. The rest of the paper is organized as follows. In Section 2, the formal definition of the PQMR problem is given. In Section 3, an ILP formula for optimally solving the PQMR problem is proposed. In Section 4, efficient heuristic algorithms with low time complexities are developed. In Section 5, computer simulations are conducted and discussed. Section 6 concludes the whole research.

2. The Definition and Complexity of the

PQMR Problem

Assumptions

To provide sufficient power for the transmission of packets along a route from a source to a destination such that each node in the route does not run out of its residual power while the data transmission takes place, the required amount of power need to be reserved along the route. Before the power can be reserved, the transmission power consumption of each node along the route has to be calculated in order to determine whether the current residual power is enough or not. Namely, the transmission power consumption of each node must be no more than its current residual power capacity. In the following, we assume that each node is able to estimate its current residual power capacity.

In the following, we are concerned with the connection-oriented traffic. To be more specific, given a pair of source and destination, a fixed route connecting the two nodes should be established to transmit all the packets originated from the source to the destination. We will define the time period of the whole transmission as a session. Therefore, in our PQMR problem, it is required to guarantee that the transmission of packets along a single route can be supported by the residual power capacity of each node along the route until the completion of the session. For simplicity, in the following, it is assumed that the number of packets transmitted during any session should be a constantσand only the transmitting power be considered (i.e., the reception power is ignored). As a result, the power (denoted as β_{i j}_, in the following discussions) required to transmit packets along link (i,

j) during a session is approximately equal toβ_{i j}_, ×σ.

Problem Formulation

We represent a MANET by a weighted graph G = (V, E), where V denotes the set of mobile nodes and E denotes the set of communication links connecting the nodes. For V, we define a residual power capacity

function

α

: V

→

R+ that assigns a nonnegative

weight to each node in the MANET. The value

α

(vi)

associated with node vi

∈ V represents the current

residual power capacity of node vi. For E, we define a

transmission power consumption function

β

: E

R

→

+

that assigns a nonnegative weight to each link in

the network. The value β associated with link (i, j) _{i j}_,

∈ E represents the transmission power that a route

will consume on that link during one session.

Under the PQRM problem we are considering, k sessions originating from k source nodes

i

s

v ∈V in

the MANET have to be connected to their individual destination nodes

i

d

v ∈ . A set R of k routes for the k V

sessions is feasible if and only if each route ri in R is a

simple path connecting source i s v to destination i d v ,

and each node v_i∈V satisfies the constraint that

∑

∈E j i, ) (

(Formula 2.1), where µ_{i j}_, = the

× ≥ i j ij i v) , , ( β µ α

number of the routes passing link( ,i j).In other words, a set of feasible routes must guarantee that the transmission of packets along each route ri from its

source i

s

v to its destination i

d do not run out of

power of any node in r

v

i until the completion of the

session.

Based on these notations and definitions, we can now formally describe the PQMR problem in our paper: given a weighted graph G=(V,E), k pairs of

source and destination nodes (vs_i,vd_i), v vsi, di∈V, a

residual power capacity function

α

: V → R+ is

defined in V, a transmission power consumption

function β : → is defined in E, find a set R of

k feasible routes.

A +

R

Example

As an illustration of the above definitions and notations, let us consider the example shown in Figure 1. In Figure 1, let nodes

1 s v , 2 s v , and 3 s v be the source nodes and nodes

1

d , d2 , and vd3 be their

corresponding destination nodes, respectively. It is not difficult to observe that there is no feasible solution in Figure 1 for the 3 sessions to be established. In fact, at most two feasible routes can be discovered (one possible instance is shown by the two bold-faced lines which connect 1 v v s v to 1 d and connect 2 v vs to d2 ,

respectively). On the other hand, if the current residual power capacity of node ₁ is increased from 10 to 15, then there exists a set of 3 feasible paths for the current PQRM problem (the new path connecting

3

v

s

v to is shown by the dotted line). Note that

3

d 1,3

v µ =2.

Given a PQMR problem, when its transmission

power consumption function

β

is an arbitrary

function, i.e., the weight assigned to a link is independent of the length of the link, we say the considered PQMR problem to be a general PQMR

problem. On the other hand, if the weight assigned to a

link is related to the Euclidean distance of the link, the associated PQMR problem is defined to be a

geometric PQMR problem.

Although the complexity of the geometric PQMR problem is unknown, the general PQMR problem has been proved to be an NP-complete problem in [5]. Note that when k = 1, the geometric PQMR problem is reduced to the power-based QoS unicast routing problem considered in [7] and can be solved in

(3)

polynomial time. When each node has very large power, such as the case in the wired network, the general and geometric PQRM problems can be easily solved by the Dijkstra’s algorithm [2].

3. An ILP Formula for Optimally Solving

the PQMR Problem

In this section, according to the principle of network flow and linear programming techniques [1], we will propose an ILP formula to find the optimal solution of the PQMR problem.

The PQMR problem is a decision problem, namely, its goal is to find whether there exists a set of feasible routes or not. On the other hand, the linear programming technique is mainly used for the optimization problem. Therefore, we need to re-form the decision PQMR problem to become an optimization problem, namely, the optimization PQMR problem: given a weighted graph G=(V, E), k pairs of source and destination nodes ( ,

i i)

s d ,

, a residual power capacity function v v

,

i i

s d

v v ∈V

α

:

V → R+ is defined in V, a transmission power

consumption function β :

A

→ R is defined in E, +

find a set R of k routes ri that sets up a session

between each source i

s

v to its corresponding estination such that i d v , , , 1 ( , ) q q k s d i j i j q i j E x β = ∈ ×

∑ ∑

is minimum, where s d_,q,q i j

x = 1 if link (i, j) belongs to the route

r

q

connecting q s v to q d ; otherwise, i j, , under

the constraint that for each v Vi

v , 0 q q s d x = ∈ , , , ( , )i j E ( )vi i j i j α ≥

∑

β ×µ ∈

, whereµ_{i j}_, = the number of sessions passing link ( , )i j .

Our ILP formula to solve the optimization PQMR problem is as follows. Minimize: , , , 1 ( , ) q q k s d i j i j q i j E x β = ∈ ×

∑ ∑

(3.1) Subject to: , , , , 1 1 0 q q q q h j s d s d i h j i v V v V x x ∈ ∈ ⎧ ⎪ − = −_⎨ ⎪ ⎩

∑

1 2 1 2 { , , , } { , , , } otherwise k k i s s s i d d d v v v v v v v v ∈ ∈ " " (3.2) , , , 1 ( ) q q j k s d i j i j i q v V x v β α = ∈ × ≤

∑∑

for each v_i∈V (3.3) , , 0,1 ( , ) , 1, 2, , q q s d i j x = i j ∈E q= " k (3.4)

Function (3.1) is the object function to minimize the total transmission power that all routes consume. Equation (3.2) is derived from the usual conservation of flow constraints. For each source, there is just one

route originated from it. Similarly, for each destination, there is just one route terminated at it. For other nodes, the net number of routes entering to it (i.e., in-flow) is equal to the net number of routes leave from it (i.e., out-flow), since they serve only as relay nodes. Inequality (3.3) expresses the constraint on the power of node. It reveals that the total transmission power consumption of a node must be equal or less than its residual power capacity. Finally, the value of s d_,q,q

i j

x is

either 1 or 0 because each link either belongs to a certain route or not.

4. Efficient Heuristic Algorithms for the

PQMR Problem

In this section, we will propose two heuristic algorithms for the PQMR problem. One is simpler and faster. The other is more efficient and its solution is very close to the optimal.

As described in section 2, when each node has very large power, such as the case in the wired network, the PQMR problems can be optimally and easily solved by the Dijkstra’s algorithm. Based on such an observation, we obtain our first simple heuristic algorithm, Dijkstra’s algorithm_based

Heuristic Algorithm_1 (DAHA_1), for the PQMR

problem. In DAHA_1, for each pair of source and destination, we first find a route with the minimum total transmission power consumption by using Dijkstra’s algorithm. Next, we check whether the route is feasible or not according to Formula (2.1). If it is, the residual power of each node in this route will be decreased by its transmission power consumption; otherwise, the found route is deleted. The details of DAHA_1 are described in Figure 2. It is easily observed that the execution time of DAHA_1 is

O (kn2).

Since the power of each node is limited, for a given pair of source and destination, the route with the minimum total transmission power consumption is not always a feasible route. A route even with more total transmission power consumption may be feasible if the nodes belong to the route have more residual power. Based on such an observation, we develop our second heuristic algorithm, Dijkstra’s algorithm

based_Heuristic Algorithm_2 (DAHA_2), for the

PQMR problem. Like DAHA_1, DAHA_2 first finds feasible routes by using Dijkstra’s algorithm. When there exist routes with the minimum total transmission power consumption which are not feasible, the links with the transmission power consumptions more than their associated nodes’ residual power are deleted and then Dijkstra’s algorithm is applied to the reduced network once more. The details of DAHA_2 are described in Figure 3.

Next, let us analyze the time complexity of DAHA_2. Note that Lines 4-7 in DAHA_2 is indeed DAHA_1. The running time of Loop 8-10 is O (

E

).

(4)

As a result, the time complexity of DAHA_2 is k

×

(O (kn2) + O ( E ) + k

×

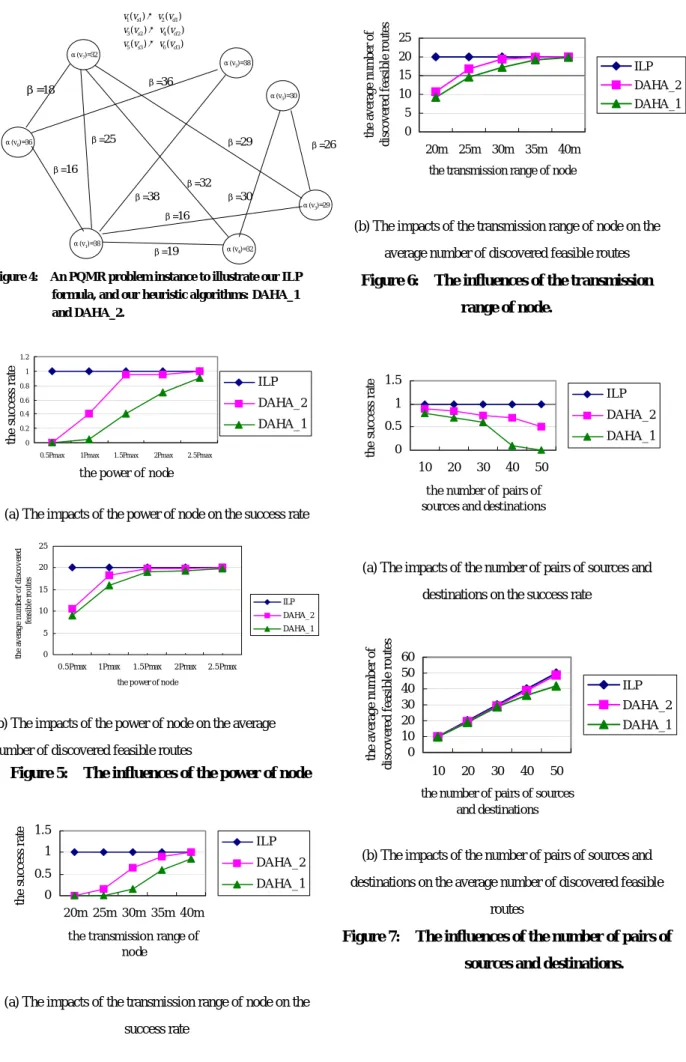
O (n2)) = O (k2n2) + O (kn2) + O (k2n2)= O (k2n2).

In the following, we will illustrate the operations of DAHA_1 and DAHA_2 with an example. When DAHA_1 is applied to the MANET in Figure 4, DAHA_1 first finds a feasible path[ ,₁ ₂ for the first pair of source and destination. Next, DAHA_1 finds

path for ] v v 3 1 4 [ , ,v v v] 2 s v and 2 d , and path ₅ ₃ ₁ ₆ for 3 v [v v v v, , , ] v_s and 3 d , respectively.

However, the last two paths are not feasible. When DAHA_2 is applied to the MANET in Figure 4, DAHA_2 first finds a feasible path [ ,₁ ₂ for

1

v

] v v s v and 1

d . In the second while loop, DAHA_2 will

find another feasible path ₃ ₅ ₄ for

2 v [ , , ] v v v v_s and 2 d v . However DAHA_2 can not find a feasible path for

3

s

v and

3

d

v . On the other hand, when our ILP formula is applied to the MANET, all the desired three feasible

paths: , , and can be found. 1 6 2 [ , , ]v v v [ , v₃ v v₁, ₄] 5 4 7 6 [ , , , ] v v v v

5. Computer Simulations

Assumptions and Definitions

In this section, we will conduct computer simulations to evaluate the performance of our ILP formula, DAHA_1, and DAHA_2 in terms of the success rate and the average number of discovered feasible routes. Due to the space limitation, only the geometry case is presented; i.e., the transmission power consumption of a link depends on the Euclidean distance between its two end points.

In our computer simulations, only the MANETs which possess all the desired feasible routes are considered. That is to say, when a MANET is generated randomly, it will first be tested by our ILP formula to determine whether it owns all the desired feasible routes. If the answer is negative, the MANET will be discarded and not used as an input to our computer simulations. Since our ILP formula can always find all the desired feasible routes if they exist, we define the success rate of our ILP formula to be equal to 100%. We define the success rate of a heuristic algorithm as the ratio of the number of cases where all the desired routes can be discovered by it to the total number of cases where all the desired feasible routes can be discovered by our ILP formula. As an illustration, given 80 MANETs which possess all the desired feasible paths, if DAHA_1 can find all the desired feasible routes in 60 cases among them, then the success rate of DAHA_1 is said to be = 75%. Similarly, since we only consider the MANETs which possess all the desired feasible routes, the average number of discovered feasible routes for the ILP formula is always equal to the desired number of feasible routes.

60 / 80

Simulation Results and Discussions

In our first simulation environment, the power of node will be varied and its influences will be observed.

The environments in our first simulation are set as follows: the MANET consists of 60 nodes located in a 100

×

100 m2 area randomly. The transmission range of each node is set to 30m. The number of pairs of sources and destinations is set to 20.

Figure 5 shows the results of our first simulation, where Pmax denotes the maximum value among the

transmission power consumptions of all the links connected to the node. From Figure 5(a), it can be observed that the success rates of DAHA_1 and DAHA_2 are increasing as the power of node is increased. The success rate of DAHA_2 is higher than that of DAHA_1 significantly. From Figure 5(b), we can see that the average number of discovered feasible routes found by DAHA_2 is very close to that found by the ILP formula in most cases.

In our second simulation environment, the transmission range of node will be varied and its influences will be observed. The environments in our second simulation are similar to our first simulation environments except that the power of node is set to the maximum value among the transmission power consumptions of all the links connected to the node.

The results presented in Figures 6(a) and 6(b) are expected. That is, the success rates of DAHA_1 and DAHA_2 are increasing as the transmission range of node is increased. This is because when the MANET is getting denser and its connectivity becomes higher, feasible routes are easier found.

In our third simulation environment, the number of pairs of sources and destinations will be varied and its influences will be observed. The environments in our third simulation are similar to our first and second simulation environments.

Figure 7(a) indicates that with the increase of the number of required routes, the success rates of DAHA_1 and DAHA_2 declines quickly. This is because the more the required routes, the more chances that several routes pass through the same node so that it has no sufficient power to supply other routes. The result in Figure 7(b) is expected.

6. Conclusions

In this paper, we have considered the NP-complete PQMR problem of searching multiple routes satisfying the power requirement in a mobile ad-hoc network. According to the principle of network flow and linear programming techniques, an ILP formula has been designed. Although our ILP formula can generate the optimal solution for the PQMR problem, its running time is very high. Based on the Dijkstra’s algorithm, two heuristic algorithms with low time complexities have been developed. DAHA_1 is simpler and faster. DAHA_2 is more efficient. In fact, computer simulations verify that the suboptimal solutions generated by DAHA_2 are very close to the optimal ones.

(5)

References

[1] G. B. Dantzig and M. N. Thapa, Linear

Programming 1: Introduction, Springer-Verlag,

Berlin, 1997.

[2] E. W. Dijkstra, “A Note on Two Problems in Connection with Graphs,” Numerische

Mathematik, vol. 1, pp. 269-271, 1959.

[3] A. Michail and A. Ephremides, “Energy Efficient Routing for Connection-Oriented Traffic in Ad Hoc Wireless Networks,” The 11th IEEE

International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), 2000, vol. 2, pp.762-766. 1 ( ) 10vs α = 3 (vd) 10 α = 1 (vd) 10 α = 2 (vd) 10 α = 3 (v) 10 α = 2 ( )v 10 α = 1 ( )v 10 α = 2 ( ) 10vs α = 3 ( ) 10vs α = β=10 β=10 β=10 β=5 β=5 β=5 β=5 β=5 β=5

[4] A. Misra and S. Banerjee, “MRPC: Maximizing Network Lifetime for Reliable Routing in Wireless Environments,” IEEE Wireless

Communications and Networking Conference (WCNC), 2002, vol. 2, pp. 800-806.

[5] P. R. Sheu and C. H. Chien, “On the Complexity of Power-Aware Multiple Routing for Mobile Ad Hoc Networks,” Proceedings of the 2004

International Computer Symposium (ICS2004), Taiwan, R.O.C., pp. 972-976.

[6] S. Singh, M. Woo, and C. S. Raghavendra, “Power-Aware Routing in Mobile Ad Hoc Networks,” The Fourth Annual ACM/IEEE

International Conference on Mobile Computing and Networking, 1998, pp. 181-190.

[7] S. Tragoudas and S. Dimitrova, “Routing with Energy Considerations in Mobile Ad Hoc Networks,” IEEE Wireless Communications and

Networking Conference (WCNC), 2000, vol. 3,

pp. 1258-1261.

Figure 1: An example to illustrate the PQMRproblem.

DAHA_1：

Input: a MANET G = (V, E), a residual power

capacity function

α

: V

→

R+, a

β

: E

→

R+, k pairs of sources and

destinations

(

,

)

i i s d

v v

,

i i Output: A set R of s d

v v

∈

V

x

≤

k

feasible routes ri connecting source i s

v

to destination i d

v

, 01. begin 02. A={ 1 1

(

v v

_s

,

_d

)

，，…， }; 2 2

(

v

_s

,

v

_d

)

(

,

)

k k s d

v

Φ = R ; 03. for each

(

v v

s_i

,

d_i

)

∈

A

04. find a route ri with the minimum total

transmission power consumption by using Dijkstra’s algorithm;

05. if ri is a feasible route (checked by Formula

(2.1)) then { ( , ) i i s d A= −A v v ;R= ∪R r_i; for each 1 2

( ,

j j

)

∈

r

_i d 1 2 j j o 1 1 ,

(

v

_j

)

(

v

_j

)

α

=

α

−

β

end }

06. end of for each

(

,

)

loop

i i

s d

v

∈

A

07. output R;

08. end of the algorithm

Figure 2: DAHA_1: a simple heuristic algorithm for the PQMR problem.

DAHA_2：

Input: a MANET G = (V, E), a residual power

capacity function

α

: V

→

R+, a

β

: E

→

R+, k pairs of sources and

destinations

(

,

)

i i s d

v v

,

i i Output: A set R of s d

v v

∈

V

x

≤

k

feasible routes ri connecting source i s

v

to destination i d

v

, 01. begin 02. A={ 1 1

(

v v

s

,

d

)

，

(

v

s₂

,

v

d₂

)

，…，

(

v

s_k

,

v

d_k

)

}; Φ = R ; 03. while

A

≠

Φ

04. for each

(

,

)

i i s d

v

∈

A

05. find a route ri with the minimum total

transmission power consumption by using Dijkstra’s algorithm;

06. if ri is a feasible route (checked by Formula

(2.1)) then {

(

,

)

i i s d

A

= −

A

v v

;

R

= ∪

R

r

_i ; for each

( ,

j j

₁ ₂

)

∈

r

_i do 1 1 j j 1,2

(

v

)

(

v

)

_{j j}

α

=

α

−

β

(

v

_s

,

v

_d end }

)

∈

A

07. end of for each loop

i i

08. for each

( , )

i j

∈

E

do

09. if

α

( )

v

_i

<

β

_i_,_j or

α

( )

v

_j

<

β

_{i j}_, then

( , )

E

=

E

−

i j

10. end of for each

( , )

i j

∈

E

do loop; 11. G = ∪ ; V E 12. for each

(

,

)

i i s d

v

∈

A

13. if i s

v

is not connected to in (checked by Dijkstra’s algorithm) then i

d

v

G

(

,

)

i i s d

A

= −

A

v v

; 14. end of for each ( , ) loop

i i 15. end of while s d v v ∈A Φ ≠ A loop 16. output R;

17. end of the algorithm

Figure 3: DAHA_2: an efficient heuristic algorithm for the PQMR problem.

(6)

β=38 β=16 β=19 β=16 β=25 β=36 β=29 _β=₂₆ β=30 β=32 β=18 _α(v 5)=30 α(v6)=36 α(v1)=38 α(v3)=29 α(v4)=32 α(v7)=32 α(v2)=38 1 1 2 1 3 2 4 2 5 3 6 3 ( ) ( ) ( ) ( ) ( ) ( ) s d s d s d v v v v v v v v v v v v → → →

Figure 4: An PQMR problem instance to illustrate our ILP formula, and our heuristic algorithms: DAHA_1 and DAHA_2. 0 0.2 0.4 0.6 0.8 1 1.2

0.5Pmax 1Pmax 1.5Pmax 2Pmax 2.5Pmax

the power of node

th e s u cces s ra te ILP DAHA_2 DAHA_1

(a) The impacts of the power of node on the success rate

0 5 10 15 20 25

0.5Pmax 1Pmax 1.5Pmax 2Pmax 2.5Pmax the power of node

th e av er ag e n u m b er o f d is co v er ed feas ib le r o u tes ILP DAHA_2 DAHA_1

(b) The impacts of the power of node on the average number of discovered feasible routes

Figure 5: The influences of the power of node

0 0.5 1 1.5

20m 25m 30m 35m 40m the transmission range of

node th e s u cces s r a te ILP DAHA_2 DAHA_1

(a) The impacts of the transmission range of node on the success rate 0 5 10 15 20 25 20m 25m 30m 35m 40m

the transmission range of node

the average number of discovered f easible routes ILP DAHA_2 DAHA_1

(b) The impacts of the transmission range of node on the average number of discovered feasible routes Figure 6: The influences of the transmission

range of node. 0 0.5 1 1.5 10 20 30 40 50

the number of pairs of sources and destinations

th e s u cc es s r a te ILP DAHA_2 DAHA_1

(a) The im urces and

destinations on

pacts of the number of pairs of so the success rate

0 10 20 30 40 50 60 10 20 30 40 50

the number of pairs of sources and destinations th e averag e nu m b er o f d isc ove re d f ea si b le r o u te s ILP DAHA_2 DAHA_1

(b) The impacts of the number of pairs of sources and e numb

destinations on the averag er of discovered feasible

Figure 7: The inf airs of

sources and destinations. routes