A linear-time algorithm for computing the diameters of the incomplete WK-recursive networks

A Linear-Time Algorithm for Computing the

Diameters of the Incomplete WK-Recursive Networks

Min-Yang Su and Gen-Huey Chen Dyi-Rong Duh

Department of Computer Science and Information Engineering, National Taiwan University, Taipei, TAIWAN

Department of Electronic Engineering, Hwa Shia Junior College, Taipei, TAIWAN

Abstract

The WK-recursive networks, which were originally proposed by Vecchia and Sanges, have sufferedfrom the rigorous restriction on the number of nodes. Like the other incomplete networks, the incomplete WK-recursive networks have been proposed to relieve this restriction. In this paper, it is first shown that the structures of the incomplete WK-recursive networks are conveniently represented with multistage graphs. This representation can provide a uniform look at the incomplete WK- recursive networks. By its aid,

a

linear-time algorithm using the prune-and-search technique is presented

for

computing the diameters

of

the incomplete WK-recursive networks.

1

Introduction

One important step on designing

a

large multiprocessor system is to determine the topology of the interconnection network (network for short). In the recent decade, a number of networks have been proposed i n the literature [I, 3, 4, 17, 19, 20, 241. Among them, the WK-recursive networks [24] own two structural advantages: expansibility and equal degree. A network is expansible if no changes to node configuration and link connection are necessary when it is expanded, and of equal degree if all its node have the same degree no matter what the size is. A network with these two properties will gain the advantages of easy implementation and low cost when it is manufactured.

The WK-recursive networks, which were proposed by Vecchia and Sanges [24], represent a class of recursively scalable networks. They offer high degree of regularity, scalability and symmetry which very well conform to a modular design and implementation of distributed systems involving a large number of computing elements. A VLSI implementation of a 16-node WK-recursive network has been realized at the Hybrid Computing Research Center [25]. In this implementation, each node was

implemented with the INMOS IMS T414 transputer, and the network processes were coded in Occam programming language. Later this prototype network was further extended to 64 nodes [25]. Recently two variants of the WK-recursive networks have been proposed in [7,81.

Although the WK-recursive networks own many nice properties [2, 5 , 6, 9-11, 12, 24, 251, there is a rigorous restriction on the number of their nodes. As will become clear in the next section, the number of nodes in a WK- recursive network must satisfy d', where b l is the size of the basic building block and t 2 l is the level of expansion. Thus, as d=4, extra 3.4'=49152 nodes are required to expand from a 7-level WK-recursive network to an 8-level WK-recursive network. All of the networks mentioned above suffer from the same restriction. To relieve this restriction, some incomplete networks such as incomplete hypercubes [ 131, incomplete star networks [14, 181, incomplete rotator graphs [16], were proposed. Recently, the incomplete WK-recursive networks have been proposed by the authors [21]. From a practical point of view, the number of nodes is considered a multiple of d , where d is the size of the basic building block. Thus, an incomplete WK-recursive network can be expanded or contracted i n units of basic building blocks.

The distance between two nodes of a network is the smallest number of links that are contained in any path between them. The d i a m e t e r of a network is the maximum distance between any pair of nodes. Since the diameter is usually considered the maximum transmission delay within a network, i t is one of the most fundamental topological properties for the network. The diameters for the incomplete star networks and the incomplete rotator graphs are still unknown, although the diameters for the star networks [ l ] and the rotator graphs [3] have been obtained. Ravikumar et. al. [18] suggested an upper bound on the diameters of the incomplete star networks. For a special class of incomplete star networks that comprise c k-stars, where I<&, the diameters have been computed [14, 181. In this paper, using the prune-and- search technique 1151, an O(r) time algorithm is proposed

for computing the diameters of the incomplete WK- recursive networks, where t is the level of expansion.

It will be shown in the next section that the structures of the incomplete WK-recursive networks can be conveniently represented with multistage graphs. In this way, the diameter problem on the incomplete WK- recurisve networks is reduced to the diameter problem on the multistage graphs. In the next section, the incomplete WK-recursive networks are formally defined, and their multistage graph representations are also introduced. In Section 3, a tight upper bound on the diameters is suggested. In Section 4, a linear-time algorithm for computing the diameters is proposed. Finally, this paper is concluded with some remarks in Section 5.

2

Incomplete WK-Recursive Networks

and Their Multistage Graph

Representations

In this section we first review the structures of the

WK-recursive networks. The incomplete WK-recursive Figure 1. The structures of K(4, 1) and K(4.3). networks are then defined as the induced subgraphs of the

WK-recursive networks. It has been shown convenient (see [21]) to express the structure of an incomplete WK- recursive network as a multistage graph. The multistage graph representation is also reviewed in this section.

The WK-recursive networks can be constructed recursively by grouping basic building blocks. Any complete graph can serve as a basic building block. For convenience, let K(d, t ) denote a WK-recursive network of level t whose basic building blocks are each a d-node complete graph, where d>l and t2l. K(d, l), which is the basic building block, is a d-node complete graph, and K(d,

t ) for t22 is composed of d K(d, t-1)'s that are connected as a complete graph. Each node of K(d, t ) is associated with a t-digit identifier. The following definition is due to Chen and Duh [2].

Definition 2.1. The node set of K(d, t ) is denoted by (a,la,.z...alaO I a i € (0, 1,

...,

d-1) for OSi5t-1). Node adjacency is defined as follows: aI~laI~z...alao is adjacent to (1) ar-1a,2

...

alb. w h e r e & M - l and &ao, and (2) a,laf.2...

aj+la,-l(rfi)i if ui#aj.l and ~,-~=a,.~= .._ =ao, where l<j<t-l and (a;)' represents j conecutive

ais.

The links of (11, labeled 0, are called substituting links. The links of (2), labeled j , are called j-flipping links (or simply flipping links). Besides, there are open links whose one end node is (a)', where O$a<d-l, and the other end node is unspecified. The open links are labeled t.

Since each node is incident with d-1 substituting links and one flipping link (or open link), K(d, t ) has

degree d . The structures of K(4, 1) and K(4, 3) are illustrated in Figure 1. Intuitively, the substituting links are those within basic building blocks, the j-flipping links each connect two embedded K(d, j)k, and the open links are left for future expansion. For example, let us consider the incident links of node 311 in Figure 1. The one to node 133 is a 2-flipping link, and the others are substituting links. Since the WK-recursive networks are recursive, K(d, t ) contains K(d, i)k, K i d , as subgraphs (subgraph and subnetwork are used interchangeably in this paper). In the following we define these subgraphs formally.

Definition 2.2. Define c,,c,.~...c;K(~, r) to be the subgraph of K(d, t ) induced by (cf~,cI.2...cp,I...alao I a; E

(0, 1,

...,

d-1) for &&r-l), where 1 I r l t - 1 and c f - ] , ct-2,

...,

c, are all integers from

{O,

1,

...,

d-1).

For exaimple, refer to Figure 1 where 31.K(4, 1) is the subgraph of K(4,3) induced by (310,311,312,313). Definition 2.3. Node a,.lnI.z

...

ala0 is a k-frontier if ak-,=

...

=ol=ao, where 153%.

Note that by Definition 2.3, a k-frontier is automatically an I-frontier for Ill&. Both end nodes of a k-flipping link are k-frontiers. An embedded K(d, r), where l<rSf-1, contains one (r+l)-frontier and d-1 r- frontiers. These d frontiers are 2'-1 distant from each other.

If we number the nodes of K(d, t ) according to their lexicographical order, then an N-node incomplete WK- recursive network is the subgraph of K(d, t ) induced by the first N nodes. Throughout this paper, we use IK(d, t ) to denote an N-node incomplete WK-recursive network, where d-k N<df and N is a multiple of d.

The coencient vector associated with an N-node IK(d, t ) is a (t-1)-tuple using d-ary numbers (bi-l, b,.~, ..., b,) satisfying N=b,~ldf-1+b1~2dP2+

...

+bid, where d ' - ' d < dr and N is a multiple of d. IK(d, t) with coefficient vector

bt-2,

...,

b,) contains b,.l K(d, t - l l ' s , b,., K(d, t-2)'s,

...,

and bl K(d, 1)'s. For l<m<t-l, the b, K(d,

m)'s

are b,lbf.~...bm+l0.K(d,

m),

bt-lbt-2

...

b,+ll.K(d,

m ) ,

...,

and

b,.lb,2...b,+,(b,-l).K(d,

m).

For example, IK(5, 6) with coefficient vector (2, 3, 0, 4, 0) contains the following subnetworks.

O.K(5, 5 ) , l.K(5, 5 )

2O.K(5,

4),

21.K(5,

4),

22.K(5, 4)

2300.K(5, 2), 230l.K(5, 2), 2302.K(5, 2) 2303,K(S, 2) See Figure 2 where the structure of IK(4, 3) with coefficient vector (3, 2) is illustrated. In the rest of this paper, a coefficient vector (bt-l, b,.2,

...,

b l ) is written as (b,-l, br-2,

...,

b;, *), provided b ; d and b;.l=bi-2= ... =bl= 0. For example, (2, 3, 0, 4, 0) is written as (2, 3, 0, 4,

*), and (2, 3, 4) is written as (2, 3, 4, *).

Let G, represent the subgraph of IK(d, t ) with coefficient vector (b,,, bl.2,

...,

b l ) induced by bI-lbl-2... (b,-l).K(d,

m),

where l2mSt-1. For example, the IK(5, 6) with (2, 3 , 0 , 4 , *) mentioned above has GS containing O.K(S, 5 ) and l.K(5, 51, G, containing 2O.K(5, 4), 2l.K(5, 4), and 22.K(5, 4), G 3 empty, G 2 containing 2300.K(5, 2), 230l.K(5, 2), 2302,K(5, 2), and 2303.K(5, 2). For easy reference, we refer to b,.1b,.2 ... b,+ii.K(d, m ) as the (j+1 )th K(d, m) of G,, where O<jsb,-l.

According to the discussion above, the structure of IK(d, t ) with coefficient vector (bt-,, b,,, ..., bj, *) can be expressed as a multistage graph, denoted by Gr.1+Gl.2+

...

+Gi. There are t-i stages, i.e., G,i, ..., and G,. For example, the multistage graph representations of IK(5, 6) with coefficient vector (2, 3, 0, 4, *) and IK(6, 10) with coefficient vector

(4,

2 , 4, 3, 4, 1, 1, 3, 1, *) are shown in Figure 3, where each K(d, m ) within G, is drawn as a circle and the links within G, are omitted for conciseness. The links between G, and G,, where t-l>m>n>i, are m- flipping links, and they are called jumping m-flipping links if m-n>l. There are min{b,, bm-l) m-flipping links connecting the jth K(d,

m)

of G, and thejth K(d, m-1) of G,,,-,, where l<j<min{b,, b m - l ] . Besides, there may exist some jumping flipping links and they can be determined according to the following theorem.

b,+lO*K(d,

m ) ,

b1.1br.2

...

bm+ll.K(d,

m),

..., bt.lbl.2 ... bm+l

3

Figure 2. The structures of I K ( 4 . 3 ) with coefficient vector ( 3 , 2,*).

(b)

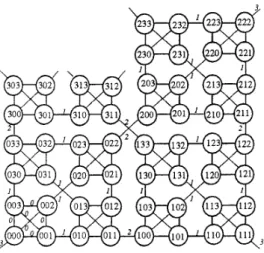
Figure 3. (a) IK(5. 6) with coeffiaent vector ( 2 . 3 . 0 , 4 , * ) and (b) IK(6, 10) with coefficient vector (4, 3, 5. 1. 1. 5, 2,5, I,*).

Theorem 2.1.[22] For IK(d, t ) with coefficient vector (bt-], bI-,,

...,

b;, *), one jumping m-flipping link exists between G, and G, if and only if bm>bm.l=bm.2= ... =bn+l<b,, where t-l>m>n>i and m-n>l. Moreover, (1) this link connects the (r+l)th K(d, m ) and the (r+l)th K(d, n ) , where r=bm.l=bm-2= ... =bn+,, and

(2) no other link exists between G, and C y , where m<nlt-1 and i<$n (i.e., no two jumping flipping links overlap).

Theorem 2.1 provides a simple way to determine all jumping flipping links from the coefficient vector (b,-l,

bIv2,

...,

bi,

*). We only need to examine (b,-l, b,.,,

...,

b;,

*) from left to right, and find a jumping m-flipping link connecting G, and G,, where

m-n>l,

if b,,,>b,.l= bm-2=

...

=bn+l<bn. Moreover, the jumping flipping link connects the (r+l)th K(d, m) of G, and the (r+l)th K(d, n ) of G,, where ~ = b , . ~ = b ~ - ~ =

...

=bn+l. Throughout this

paper, we use J to denote the jumping u-flipping link that connects the wth K(d, U) of G, and the wth K(d, v) of

G,,

where u-v>l (refer to Figure 3).

Let D G m denote the diameter of G,. Since G, contains b, K(d, mYs that are completely connected, we have DGm=2Dm+1 if b,>l, and D, =D, if b,=l, where D,=2,-1 is the diameter of K(d, m) 121. It has been shown in [2] that the distance between any two

m -

frontiers of K(d, m) defines D,. Since the topology of IK(d, t ) is much irregular than that of K(d, t ) , it is not surprising to see that computing the diameter of IK(d, t ) is far more difficult than computing D,. In fact, we are convinced that the diameter of IK(d, t ) cannot be expressed with a formula. In subsequent sections, we use ID, to denote the diameter of IK(d, t ) , and d(A, B ) to denote the distance between any two nodes A and B in IK(d, t ) .

U, v

m

3

An

Upper Bound

on IDt

An upper bound on ID, is proposed below.

Theorem 3.1. For IK(d, t ) with coefficient vector (bl-l, b,,, ..., bi, *), where 1 S t - 1 , we have ID,S2t+2t-1- 2'-1.

Proox We prove this theorem by induction on i. Induction basis. When i=t-1, b,.122 and lDFDG,~,=2'-1. This theorem holds.

Induction hypothesis. Assume this theorem holds for i2m+l, where l<mV-2. That is, 1D,121+2t-1-2m+1-1. Induction step. We proceed with i=m. Suppose U and V are any two nodes of the IK(d, t ) . If they both reside in GI-1+GI-2+

...

+G,+l, we have by assumption d ( U , V ) l 2'+2'-1-2m+1-1<2r+2f-1-2m-1. If they both reside in C,, we have d( U , V)<2Dm+ 1 =2m+I- 1<2I+21-1-2m- 1 because mit- 2. So, for completeness, we assume U and V reside in GI and G,, respectively, where t-l>l>m, in the following discussion. Since there is at most one jumping flipping

link incident on G, (known from Theorem 2.1). we consider the following two cases.

Case 1. There is one jumping flipping link connecting G, and

Gk

for some k, t-l>k>m+l.

Suppose ( w l , w 2 ) is the jumping flipping link, where

w,

E

Gk

and

w2

E G,. We first assume E l . Clearly d ( U , V)Sd(17, wl)+l+d(w2, V ) . Since d(wz, V)ID,_S 2m+l-l and d(U, ~ ~ ) < 2 ~ + 2 ~ - ~ - 2 k - l by assumption, we have d( U, V)12f+2t-1-2k+2m+1-1 <21+2t-1-2m-1 because k&+2.

On the other hand, if bl, we have b~->b~.l=bk-2=

...

= bl=

...

=bm+l.tb, by Theorem 2.1. This implies that there is a path between U and V whose length is bound above V)<21+1-1<2is+2z-1- 2"-1 because 1 9 2 in &us situation. by (D1+1)+(Dl.1+1)+

...

+(Dm+l+l)+DG m =2'+'-1. SO, d(U,

Case 2. No jumping flipping link is incident on G,. We firsl. assume b,+l<b,. If bl=min{b,. bl-1,

...,

b,],

there is a path between U and V whose length is bound So, d( U , V)5;2'+1-1<2z+2t-1-2m-1 because 19-1 and mv-2. Otherwise, let b,=min( bl, blbl, ..., b,), where m+l<r<l (if r=m+l, there is a jumping flipping link incident on G,). By Theorem 2.1 there is exactly one jumping flipping link. between G, and G,, where b,>bx.l=

...

=b,=

...

=by+&?. Let

(wI,

w 2 ) be the link and w 1 EG,, w 2

E C y . Clear1:y d ( U , V)Qi(U, w,)+l+d(w,, V). In addition, d ( U , w1)12'+2r-1-2x-1 by assumption, and there is a path between w . ~ and V whose length is bound above by 2y-1. Hence, d( U , V)121+2l-l-2x+2Y+1+2~-1 <21+2r-1-2m-1 because n y + l and y>m.

On the other hand, if bm+]2b,, one (m+l)-flipping link connects each of the K(d, m)'s contained in G, to G,+]. Since the distance between U and any node of G,+] is not great'er than 21+21-1-2m+1-1 (by assumption), we have d( U , V ) S 21+21-1-2m+1-1 +(D,+l )=2f+21-1-2m- 1.

above by (Dfll)+(Di.1+1)+

...

+(Dm+1+1)+0Gm=2'+'-1.

(D, +1)+(D',.1+1)+(DY-2+1)+

...

+(Dm+l+l)+D, =2Y+l+

Y m

Q.E.D. Note that the upper bound we proposed in Theorem 3.1 is tight for general IK(d, 1 ) . This can be seen as follows. Consider a particular IK(& t ) whose coefficient vector (ble1, b,~,

...,

b,, *) satisfies bl-l>b,.?2br-32

...

Zb,. The distance between (bl-l-l)l and bt.,bl.2...bl+10(l)~ IS

equal to (D,:, 1+1 )+(D,2+1 )+(D,.3+1)+

...

+(D,+1+1)+DI= 2't2'-'-2'-1, which matches the upper bound. However, for most instances of IK(d, t ) , their diameters are smaller than the upper bound. To calculate the actual values, an O(t) time algorithm is proposed in the following section.

4

An

0

( t )

Time

Algorithm

for

For IK(d, t ) with coefficient vector @,-I, br-2,

...,

bi, *), its diameter is simply DG,-, if i=t-1. Thus we assume 14iIt-2 throughout this section. Moreover, we let U and V denote one farthest pair of nodes in the IK(d, t ) , and assume that U precedes V lexicographically. Our algorithm aims to identify U and V and then compute their distance. Note that d(U, V)=ZD,.

It is impossible for both U and V to reside in Gr-2+

...

+Gi. The reason is explained as follows. If both U and V reside in G1-2+Gr-3+

...

+ G , then by Theorem 3.1 we have d( U , V)12~-1+2t-2-2i-1 because Gf.2+Gt-3+

...

+G, itself forms an IK(d, t-1) with coefficient vector (bf.2, bt.3,

...,

b,, *). However, when b,l>l, the distance between any two t-frontiers is 2I-1; when b,l=l, the distance between a t-frontier in GI.] and a (t-2)-frontier (but not a (t-1)-frontier) in is at least 2f-1+2f-2-1. They both are greater than 21-1+2f-2-2i-1. Hence, U or both U and V reside in

Note that there are d-1 (t-1)-frontiers and one t- frontier for each K(d, t-1) within Observing the topology of IK(d, t ) , it is not difficult to see that for any K(d, t-1) within say x.K(d, t-1) (05~4b~-~-l), we have

d(v,

(x)')2d(v, w) for any two nodes v P x . K ( d , t-1) and w ~ x . K ( d , 2-1). So, U can be a t-frontier of some K(d, t-1) within and consequently V is an r-frontier of some K(d, r) within G,, isrst-1. Therefore, we have the following observation without further explanation.

Observation 4.1. For IK(d, t ) with coefficient vector (b,,, bt.2, ...,

bi,

*), U can be a t-frontier of some K(d, t-1) within and V can be an r-frontier of some K(d, r ) within G, where is&-1.

When b,.l=l, ID, can be computed as follows. Theorem 4.1. For IK(d, t ) with coefficient vector (1, br.2, ..., b;, *), ID, can be computed in O ( t ) time as follows

(1) If bj<1 for all isjsr-1, ID, =

C ~ J

- 1

1 9 J < f - I

b, # O

(2) Otherwise, IDf = 2'

+

2'"

-

1, where k=max I k < j < f - l

bj #O

iSj9-1

and bj22

1,

Proof. According to Observation 4.1, we can let

U=(O)l. If bj<l for all i s j s t - 1 , at most one K ( d , j ) is contained in Gjand all of them are linearly connected. Hence, V=br-lbl-2...bi+10( 1)' is one farthest node from U ,

and d(U, V) is computed as the summation of (D,+l) for

all j E ( m I b m d and i < m l t - l ) plus D , , which is

simplified to 2' - 1. Note that the selection of V is

iijSt-1

bj#O

not unique.

On the other hand, since b 2 2 , we have D,k=2k+1-1. Let w be the (k+l)-frontier of b,-lb,-2...bk+10.K(d,

k)

(within G k ) . It is clear that V must reside in Gk+Gk-l+

...

+Gi and d ( U , V)=d(U, w)+d(w, V). Assume v belongs to

Gk-]+

...

+Gi, say

v

E G,, isrsk-1. It is not difficult to

see that d(w, v ) is not greater than the summation of (Dj+l) for all j E { m I b,d and r < m l k } plus DG,, which is at most P+'-1. However, w and b,lb,2...bk+ll(l)k are one farthest pair of nodes in Gk, and their distance is D,t=2k+1-12d(w, v). This implies V can be b1.1b1-2

...

b k + l 1 ( 1 )k. The value d( U , V ) is computed as the summation of (D,+l) for all j E [ m I b m d and k < m l t - l ] plus D,; which is simplified to 2'

+

2'" - 1.

k < i 9 f - 1

b; #O

Q.E.D. In the rest of this section, we concentrate our attention on b,.1>2. We first show that IK(d, f) with coefficient vector ( b f . ] , br.2, ...,

bi,

*) can be pruned appropriately so that the pruned structure has the same diameter. We define Zj=min{ b,-l, b,) for all isjst-1. The pruned structure is obtained by removing from IK(d, t )

bf-lb,-*...bj+l(b,-

l ) . K ( d , j ) if Zj<bj for all iSj<t-l. For example, consider IK(d, 6) with coefficient vector (2, 3,

4, 1, *). We have 55'2, ?;,=2, b3=2, b 2 = l , and the pruned structure contains O.K(d, 5 ) , l.K(d, 5 ) , 20.K(d, 4), 21,K(d, 4), 230.K(d, 3), 231.K(d, 31, and 2340.K(d, 2). The pruned structure is actually a subgraph of the IK(d, t ) . Let denote the diameter of the pruned structure of IK(d, t ) . As proven in [211, we have z f = I D f .

b,.lbl.2

...

b;+]Z;.K(d,j), bf.1b,.2...bj+1( J , + l ) . K ( d , j ) ,

...,

-

-

Theorem 4.2.[21] For IK(d, t ) with coefficient vector ( b l - ] , br-2,

...,

bi, *), we have Er=ID, for bf.]>2.

See Figure 4(a) which is the pruned structure of IK(6, 10) with coefficient vector (4, 3, 5 , 1, 1, 5 , 2, 5 , 1, *) (illustrated in Figure 3(b)). In Figure 4(a), we have

defined

E x

( i 9 s t - 1 ) to be the subgraph of IK(d, t ) with coefficient vector ( b f - ] , bf-2,

...,

bi, *) induced by the nodes of

bf.lbr.2...bx+10.K(d,

x), b , - ~ b ~ - ~ . . . b ~ + ~ l . K ( d , x ) ) ,

Now is the time to present our algorithm for computing the diameter of

IK(d,

t ) with coefficient vector

br-2, ..., b,, *), where b,.l22. The algorithm consists

G9 G8 G7 G6 G5 G4 G3 G2 G1 3 U

O--o

0

J 4 . 2

0

'9,7

0

0

0

4 (c) Figure 4. An example.

of five stages, and it can identify U and V and compute

d f U , V ) in O ( t ) time from

zf-l,

z f - 2 ,

...,

6i.

In the following the five stages are described one after another.

store xl, x2,

...,

x , in a linked list L . If no feasible jumping flipping link exists, then L is empty.

For the example of Figure 4(a), x1=4, x2=2, and L=(4, 2). Bty the aid of Theorem 2.1 Stage 1 can be completed in O(t) time.

Stage 2. Determine a=max(

r

I I

e

L and 19-S5r.1). If

a=l or no feasible a exists, U and V are determined as (0)l and ( l)f., respectively, and d(U, V) is computed as 2'- 1. If

d ,

U is determined as the t-frontier of the ath K(d, t-1). For the. latter case, remove from L those values that are greater than a.

If a=l or no feasible a exists, the execution will terminate. If a22, L may become empty or contain e,> e2>

...

>ek9

and the execution then proceeds to the next stage. For the example above, -3, U is determined as (2)" and L contains el=2 only. Clearly Stage 2 can be completed in O(t) time.

Stage 3. Determine mo as the least index I such that bs2a for t- 12s2r. If L contains e1>e2>

...

>ek, determine m l , m 2 ,

...,

m k sequentially as follows: ml=min { r I

6,>el and Zs2e1-l for m,>s>r), m2=min( I I 6 2 e 2 and b,>e2-l for m i x > ! - ) ,

...,

and m,=min(

r

I &?ek and 6,>ek-1 for mk-l >.or).

-

-

Note that t-l>m,,>m,>

...

>mk.,>m,2i. In the example above, since -3, k=l, and el=2, we have m,,=l, ml=2. The values m,,, m l ,

...,

mk can be determined in 00) time tiy scanning

J f - l ,

5r-2,

...,

6 ; from left to right.

-

Stage 4. The pruned structure is further pruned. The second pruned structure is obtained by removing from the first pruned structure br-lbt.2...bj+i bj*K(d, J ) , br-lbl-2

...

bj+l( 6;+l).K(d,j),

...,

b,-lbf-2...b,+l( 6;-l).K( d , j ) if

gj<

6,,

where iij=a for all t-1Lj2mo; bj=min(e,

6;)

if e,>l and

z,=6,

if e,=l for all m$J<m,-l and I l r A k ;

zj=z,

for all iSj<mk if m p i .

-

-

-

-

-

= 5

-

-

-

-

-

-

-

_{In the example, we have bg=3, b8=3, b7=3, b6=l,}

b5=1, b4=:2, b3=2, 6,=2, and b l = l Refer to Figure

Yl,ZI Y z r Z * Y"9Z" 4(b) where 'we define

E x

(iQ5t-1) to be the subgraph of

IK(d, t ) with coefficient vector (bl-l, bn.2,

...,

bj. *)

-

-

-

=

-

-

-

-

Stage 1. Scan b,.l, b r - 2 ,

...,

b ; from left to right and determine in sequence J"' , J ' I ,

...,

J '* so that x1>x2>

... >x,. That is,

J,"', is the first one encountered

~ 1 7 4 1

induced by the nodes of b,.lbr-2

...

b,,lO.K(d, x), b,.,b,.

YJ.ZJ YJ+lAJ,l' 2...bx+11.K.(d, x ) ,

...,

and b , . , b r - 2 . . . b , + l ( ~ , - 1 ) . K ( d , x)).

in the scanning, each

4,:

between J and J xJil where

-

-

- l<j<n, has wa,, and each J after

'

J

has w a n . Then Clearly, it takes O(t) time to determine

gt-l,

&t.2,

...,

b,.

For the convenience of explanation, we define intervals I,,

Zl,

...

as

follows. If L is empty, define

Z,=[m,,

t-11 and Il=[i, mol, where Il exists only when i<m,. If L is not empty, define Z,=[m,, f-11, Zr=[mr, mr.l] for l l r l k , and Zk+l=[i,

mk],

where Zk+l exists only when i<mk (refer to Figure 4(b)). We regard i as mk+l if Zk+l exists (i.e., Zk+l=[mk+l, mJ). For each interval I,=[g, h ] , we define S j to be the set of jumping flipping links that

are

contained in

Z,+E.,.,+

...

+G,. Note that according to the definitions of

m,, ml,

...,

mk,

when L is not empty, we have IS,I=O, ISr121 for l l r l k , and ISk+ll=O provided

Ik+'

exists. When L is empty, we have IS,I=O and I S I M provided Il exists.

=

Stage 5. If there exists only one interval Z,=[mo, t-11 (i.e., m,=i), V is determined as the f-frontier of the ( a - 1)th K(d, t-1) within and d(U,

V)

is computed as 2'-l. Otherwise, suppose there are k-1 intervals,

I,, Z1,

...,

Il.l.

Then V and d(U, V) can be determined according to the following procedure.

4.1. dis t 2'-2"0.

4.2. For each interval, say Zj=k, hl, in the sequence of 11, 1 2 , ..., 11.2, if S j contains only one jumping flipping link, say J ', and y-z=2, then dis t d i ~ + 2 ~ + ' - 2 ~ - ' - 2 g . Otherwise, letting J x be the one with maximum y in

Sj,

V t b,.lb,. 2...b,,0(l)Y-1, d(U, V) t dis+2h+1-2y-1-1, and the

execution terminates.

4.3. Suppose Il.'=[i, c]. If ISl.lI=O, then V t b , . l b r . 2

. . . b j + l O ( l ) i and d ( U , V) t d i s + 2 ' + ' - 2 ; - 1 .

Otherwise, letting J be the one with maximum y in SI.', two cases are considered as follows.

Case 1. x>l.

V t b,,b,2...by0(l~-1 and d ( U , V) c dis+2'+l-

2y-'-1. Case 2. x=l. V t b,lb,-2...bk+ll(l)k and d ( U , V ) t dis+ Y I Z Y,Z Y , Z -

2'

+

2k+1 - 1 , where k=max{ s I 5,22 and

i<

k < j 5 c

-

-

bj f O

s l z } . If no feasible k exists, then V t b,.lb,.2...

6;+10(1);andd(U, V ) t d i s + c 2 ' - 1 .

i < j < C b j # O

-

For the example above, there are three intervals: Z0=[7, 91, 1,=[2, 71, and 12=[1, 21. Initially, we have d i ~ 2 l O - 2 ~ which represents the summation of D9+1+D8+ l+D,+l. Next, since S l = ( J

1,

the execution terminates

794

2

with V=4350(1)6 and d(U, V)=(210-27)+(28-26-l), where 28-26-1 represents the summation of D7+1+D6.

So,

for IK(6, 10) with coefficient vector

(4,

3, 5, 1, 1, 5, 2, 5, 1, *), U=(2)lo and V=4350(1)6 are one farthest pair of nodes and the diameter is d(U, V)=21°+26-1 which represents the summation of D 9 + l + D 8 + l + D 7 + l + D 7 + l + D 6 (refer to Figure 4(c)). Stage 5 can be completed in O(t) time.

Lemma 4.1.[21] In Stage 2, if a=l or no feasible a: exists, then d ( ~ , v)=IDp21-1. Otherwise, ( a - l ) , is a feasible node for U.

Lemma 4.2.[21] In Stage 4, the diameter of

-

-

-

-

Gl.l+E,.2

+

...

+ E ;

is equal to

E t .

Lemma 4.3.[21] Node V determined in Stage 5 satisfies d( U , v)= zt.

Recall that I D ~ D G C l for IK(d, t ) with coefficient vector (bl.l, *). Combining Theorems 4.1, 4.2, Lemmas 4.1, 4.2, and 4.3, we reach the main conclusion of this section as follows.

Theorem 4.3. For IK(d, t ) with coefficient vector (b,.', br-2,

...,

b;, *), l<i<f-l, ID, and a feasible pair of nodes U and V such that d( U , V)=ID, can be determined in O ( t ) time.

5 Concluding Remarks

Computing the diameter for an incomplete network is far more difficult than that for a complete network. The reason is that complete networks of different sizes preserve great topological similarity, whereas incomplete networks may have a significant difference i n their topologies. For example, K(d, t ) looks very similar to K(d, t-l), whereas two IK(d, t)'s with different coefficient vectors may look very unlike in their topologies. The diameter is still unknown for the incomplete star networks [14, 181 and the incomplete rotator graphs 1161, although i t has been well solved for the star networks [I] and the rotator graphs [3].

In this paper, by the aid of the multistage graph representation, we first suggested a tight upper bound on the diameters of the incomplete WK-recursive networks. Then, we proposed a linear-time algorithm for computing the diameters. The algorithm adopts the prune-and-search technique [15] which has proven an efficient method for solving problems from operations research and computational geometry. In the algorithm GI-1+Gt-2+ ...

+ci

is first pruned to form a reduced structure

E,.1+C1-2+

+

zi.

All these three structures, although different in their sizes, have the same diameter. Thus, the diameter of

ct-l

+

Ez-2+

...

+ E i

is computed as the diameter of Gt-I+Gz-2+ More topological properties, including the connectivity and hamiltonicity, can be found in 1211. Besides, a shortest-path routing algorithm and a broadcasting algorithm have been presented in [223 and 1231, respectively. The authors are now trying to solve more problems on the incomplete WK-recursive networks.

-

-

... +Gi.

References

S. B. Akers and B. Krishnamurthy, "A group- theoretic model for symmetry interconnection networks," iEEE Trans.

on

Computers, vol. 38, no. 4, pp. 555-566, 1989.

G. H. Chen and D. R. Duh, "Topological properties, communication, and computation on WK-recursive networks," Networks, vol. 24, no. 6, P. Corbett, "Rotator graphs: an efficient topology for point-to-point multiprocessor networks," IEEE Trans. on Parallel and Distributed Systems, vol. 3, no. 5, pp. 622-626, 1992.

K. Day and A. Tripathi, "Arrangement graphs: a

class of generalized star graphs," information Processing Letters, vol. 42, no. 5 , pp. 235-241, 1992.

D. R. Duh and G. H. Chen, "Topological properties of WK-recursive networks," J. of Parallel and Distributed Computing, vol. 23, no. 3, pp. 468- 474, 1994.

D. R. Duh and G. H. Chen, "On the Rabin number problem," submitted.

R. Fernandes, "Recursive interconnection networks for multicomputer networks," in Proc. of the Int. Con5

on

Parallel Processing, pp. 76-79, 1992. R. Fernandes and A. Kanevsky, "Hierarchical WK- recursive topologies for multicomputer systems," in Proc. of the Int. Conf.

on

Parallel Processing, vol. R. Fernandes, D. K. Griesen, and A. Kanevsky, "Efficient routing and broadcasting in recursive interconnection networks," in Proc. of the Int.

Conk on

Parallel Processing, 1994, pp. 51-58. R. Fernandes and A. Kanevsky, "Substructure allocation in recursive interconnection networks," in Proc. of Inte Con$ on Parallel Processing, vol. 1,

pp. 303-317, 1994.

1, pp. 315-318, 1993.

1993, pp. 319-322.

U11 R. Fernandes, D. K. Friesen, and A. Kanevsky, "Embedding rings in recursive networks," in Proc. of Int. Symp. on Parallel and Distributed Processing, Oct. 1994, pp. 273-280.

[12] A. Iazzetta, C. Sanges, and U. Scafwri, "Special multicast wormhole routing for WK-networks," manuscript.

1131 H. P. IKatseff, "Incomplete hypercubes," I E E E Trans. on Computers, vol. C-37, no. 5 , pp. 604- 608, 1988.

[14] S . Latifi and N. Bagherzadeh, "Incomplete star: an incrementally scalable network based on the star graph," IEEE Trans.

on

Parallel and Distributed Systems, vol. 5 , no. 1, pp. 97-102, 1994.

[15] D. T. Lee and F. P. Preparata, "Computational geometry

-

a survey," IEEE Trans. on Computers, [16] S. Ponrmswamy and V. Chaudhary, "Embedding of cycles in rotator and incomplete rotator graphs," in Proc. of Int. Symp. on Parallel and Distributed Processing, Oct. 1994, pp. 603-610.

1171 F. P. IPreparata and J. Vuillemin, "The cube- connected cycles: a versatile network for parallel computation," Communications

of

the ACM, vol. 24, no. 5 , pp. 300-309, 1981.

[18] C. P. Ravikumar, A. Kuchlous, and G. Manimaran, "Incomplete star graph: an economical fault-tolerant interconnection network," in Proc. of lnt. Conf.

on

Parallel Processing, vol. 1, 1993, pp. 83-90. [19] M. R. Samatham and D. K. Pradhan, "The de Bruijn

multiprocessor networks: a versatile parallel processing and sorting networks for VLSI," IEEE Trans.

on

Computers, vol. 38, pp. 567-581, 1989. [20] H. S. Stone, "Parallel processing with the perfect

shuffle," IEEE Trans.

on

Computers, vol. 20, no. [211 M. Y. Su, G. H. Chen, and D. R. Duh, "Topological properties of incomplete WK-recursive networks," Tech. Rep. 95-06, Dept. of Comput. Sci. and Info. Engg., National Taiwan Univ., Taipei, Taiwan, March 1995.

1221 M . Y . Su, G. H. Chen, and D. R . Duh, "A

shortest-path routing algorithm for the incomplete WK-recursive networks," Tech. Rep. 95-07, Dept. of Comput. Sci. and Info. Engg., National Taiwan Univ., 'Taipei, Taiwan, July 1995.

1231 M. Y . Su, G. H. Chen, and D. R.. Duh, "A broadcasting algorithm for the incomplete WK- recursive networks," in Proc. of Inter. Symposium on Panallel Architecture, Algorithm, and Networks (ZSPAM, 1996, to appear.

1241 G. D. Vecchia and C. Sanges, "A recursively scalable network VLSI implementation," Future Generation Computer Systems, vol. 4, no. 3, pp. [25] G. D. Vecchia and C. Sanges, "An, optimized broadcasting technique for WK-recursive topologies,

I ' Future Generation Computer Systems, vol. 4, no.

vol. C-33, pp. 1072-1101, Dec. 1984.

2, pp. 153-161, 1971.

235-243, 1988.