結合載波間干擾分集技術於正交分頻多工系統之編碼技術研究

國 立 交 通 大 學

電信工程學系

碩 士 論 文

結合載波間干擾分集技術於

正交分頻多工系統之編碼技術研究

CP-reduced Coding Techniques with

ICI Diversity Combining for OFDM Systems

研究生：白政田

結合載波間干擾分集技術於

正交分頻多工系統之編碼技術研究

CP-reduced Coding Techniques with

ICI Diversity Combining for OFDM Systems

研究生：白政田 Student: Cheng-Tien Bai

指導教授：王忠炫 Advisor: Chung-Hsuan Wang

國立交通大學

電信工程學系碩士班

碩士論文

A Thesis

Submitted to Department of Communication Engineering

College of Electrical and Computer Engineering

National Chiao Tung University

in Partial Fulfillment of the Requirements

for the Degree of

Master of Science

in

Communication Engineering

February, 2009

結合載波間干擾分集技術於

正交分頻多工系統之編碼技術研究

學生：白政田 指導教授：王忠炫

國立交通大學電信工程學系碩士班

摘要

正交分頻多工是一個引人關注的傳輸技術，此技術可有效地克服多重路徑通 道的時間衰褪效應藉由在每個符元前加入循環字首。然而，使用循環字首的需求 造成了傳輸上多餘的負擔，並造成通訊系統吞吐量的下降。直接將循環字首縮短 可以改善頻譜效益卻會引入符元間干擾和載波間干擾這些不理想的效應，使得整 體系統效能受到限制。為了提升縮短循環字首之正交分頻多工系統的效能，吾人 因而進行結合載波間干擾分集技術於正交分頻多工系統之編碼技術研究。若將子 載波視為虛擬的天線，縮短循環字首之正交分頻多工系統在載波間干擾下的通道 可等效地視同一個虛擬的多重輸入多重輸出通道。此外，輔以空頻編碼的觀念， 吾人亦發現使用不足的循環字首所引起的載波間干擾其實可當作一種頻率分集 增益。本論文中，吾人基於縮短循環字首之正交分頻多工系統所造成的等效多重 輸入多重輸出通道下研發虛擬的空頻編碼技術，同時以理論分析來探討此虛擬空 頻編碼可達之分集增益上界，並提出相應之設計準則以供發展具良好效能之虛擬 空頻編碼。從模擬結果中顯示，相較於傳統的編碼正交分頻多工系統而言，吾人 之編碼技術不僅能夠達到較高之分集增益進而提升錯誤率，同時擁有更高之資料 傳輸速率。

CP-reduced Coding Techniques with ICI Diversity

Combining for OFDM Systems

Student: Cheng-Tien Bai Advisor: Chung-Hsuan Wang Department of Communication Engineering

National Chiao Tung University

Abstract

Orthogonal frequency division multiplexing (OFDM) is an attractive transmission tech-nique, which effectively deals with the delay spread of the multi-path channel by appending a cyclic prefix (CP) in every OFDM symbol. However, the necessary insertion of CP pro-duces a transmission overhead and repro-duces the throughput of the communication systems. A direct reduction of CP can improve the spectral efficiency but also introduces the un-desired inter-symbol interference (ISI) and inter-carrier interference (ICI), hence limiting the overall system performance. To enhance the performance of the CP-shortened OFDM system, the CP-reduced coding techniques with ICI diversity combining for OFDM systems are studied here. Actually the ICI corrupted channel of the CP-reduced OFDM system can be viewed as a virtual MIMO channel when we regard the subcarriers as the virtual anten-nas. And the ICI induced by insufficient CP can be viewed as a sort of frequency diversity by the concepts of space-frequency coding (SFC). In this thesis, we investigate the virtual space-frequency coding techniques based on the effective MIMO channel of the CP-reduced OFDM system and propose the corresponding design criteria to develop good virtual space-frequency codes. The maximum achievable diversity order of the virtual space-space-frequency code is determined by the theoretical analysis. Simulation results are also provided to show that the proposed coding schemes not only achieve higher diversity order to enhance the error performance but also have higher data rate compared with the conventional coded OFDM systems.

誌謝

回首來時路，感謝指導教授王忠炫博士兩年半以來對於資質努鈍

的我，成功地扮演好學術燈塔的角色，給予我充分的自由度去犯錯並

從中學習成長，於茫茫學海當中找到自己的方向。除了學術之外，老

師亦從日常生活的點滴中，教導我做人做事的道理，使我多所裨益。

您的諄諄教誨與提點我都會放在心中，謝謝老師。

再來要感謝實驗室的博班學長大師兄，在我在面對未知的問題

時，樂於和我討論激盪想法，提供我更多元的想法與模擬上的傳承，

並且在研究上遇到困難時，給予我鼓勵和希望，也謝謝你包容我的急

性子和龜毛。大師兄對於學術上的熱情和執著，是我追尋的榜樣，你

是最讚的博班學長!一定可以成為 GPW 的!祝福你!

謝謝女友和家人一直以來在生活上和精神上的支持，提供我心靈

可以休憩的避風港，不求回報地給我勇氣和力量迎向挑戰和挫折。謝

謝家人，總是以我為第一優先，讓我無後顧之憂的學習研究。謝謝女

友，假期不辭辛勞的跑來陪我窩實驗室當約會，一同承受這些本不屬

於你的壓力，真是辛苦妳了。

接下來要感謝一起打拼的應屆同學老蔡、一哥、偉帆、阿尼，學

長小民、力仁、阿寶、蓬麟、賴桑、慶和，以及學弟妹郭胖、標、白

兔，一起吃苦的幸福總是特別的鮮美，而這段研究所的日子能和你們

共同經歷、並肩作戰，是再美好不過的事情!

最後要感謝的還有同實驗室的施施、Duck、振偉、宏益、冠驛、

冠亨、KV、吉祥、喜滋滋，感謝你們天天在實驗室散播歡樂散播愛，

為沉悶的研究生活增色不少，天天見面的我們就像是兄弟一般，這份

專屬於 LAB708 的情誼我會好好珍惜的。最後，感謝其他實驗室的夥

伴瑋哥、D2、交大吳尊、大頭、LAB711 以及大學同學 kyme、媽你

個 B、阿德、聖偉，謝謝你們給我鼓勵，心情低落時陪我解悶，豐富

我的生活和眼界。

如今碩士論文終於完稿，謹以野人獻曝的心情，將此論文，獻給

實質上以及無形中幫助完成論文的你們。

Contents

Chinese Abstract I

English Abstract II

Acknowledgement III

List of Figures VI

List of Tables VIII

1 Introduction 1

2 Overview of OFDM systems 4

2.1 System Model of OFDM Systems . . . 5

2.2 Cyclic Prefix, Inter-symbol Interference and Inter-carrier Interference . . . . 6

3 Reviews of Space-Time Coding and Space-Frequency Coding 10 3.1 Space-Time coding . . . 11 3.1.1 System Model of STC . . . 11 3.1.2 Design Criteria of STC . . . 11 3.2 Space-Frequency coding . . . 14 3.2.1 System Model of SFC . . . 15 3.2.2 Design Criteria of SFC . . . 16

4 CP-reduced Coding Techniques with ICI Diversity Combining for OFDM

Systems 19

4.1 System Model of OFDM Systems . . . 19 4.2 Pairwise Error Probability Analysis . . . 20 4.3 Maximum Achievable Diversity and Design Criteria . . . 25 5 Simulation Results 30 6 Conclusions and Future Works 41 Appendix A: Proof rank (Φ) = L + 1 44

List of Figures

2.1 System model of OFDM Systems. . . 5 2.2 Stylized plot of time-domain OFDM symbol with CP of G samples. . . 6 2.3 CP-OFDM with sufficient CP and insufficient CP . . . 6 2.4 Stylized plot of the time-domain and frequency-domain OFDM symbols with

sufficient CP. . . 7 3.1 System model of STC. . . 12 3.2 System model of SFC. . . 15 4.1 Conventional SISO-OFDM systems can be viewed as virtual MIMO-OFDM . 20 5.1 BER of CP-sufficient OFDM, CP-free OFDM with perfect ISI canceler, and

SFBC coded CP-free OFDM equipped with perfect ISI canceler correspond-ing to SFBC4×2 and SFBC4×4 for N = 4, L = 1. . . . 37

5.2 BER of CP-sufficient OFDM, CP-free OFDM with perfect ISI canceler, and SFBC8×8 coded CP-free OFDM with perfect ISI canceler for N = 8, L = 1. 37

5.3 BER of CP-sufficient OFDM, CP-free OFDM with perfect ISI canceler, and SFBC coded CP-free OFDM equipped with perfect ISI canceler correspond-ing to SFBC4×2 and SFBC4×4 for N = 4, L = 2. . . . 38

5.4 BER of CP-sufficient OFDM, CP-free OFDM with perfect ISI canceler, and SFBC8×8 coded CP-free OFDM with perfect ISI canceler for N = 8, L = 2. 38

5.5 BER of CP-sufficient OFDM, CC1CP-sufficient OFDM, CP-free OFDM, CC1

CP-free OFDM with perfect ISI canceler, and CC2CP-free OFDM with perfect

ISI canceler for N = 4, L = 1. . . 39 5.6 BER of CP-sufficient OFDM, CC1CP-sufficient OFDM, CP-free OFDM, CC1

CP-free OFDM with perfect ISI canceler, and CC2CP-free OFDM with perfect

ISI canceler for N = 4, L = 2. . . 39 5.7 BER of CP-sufficient OFDM, CC1CP-sufficient OFDM, CP-free OFDM, CC1

CP-free OFDM with perfect ISI canceler, and CC2CP-free OFDM with perfect

ISI canceler for N = 8, L = 1. . . 40 5.8 BER of CP-sufficient OFDM, CC1CP-sufficient OFDM, CP-free OFDM, CC1

CP-free OFDM with perfect ISI canceler, and CC2CP-free OFDM with perfect

ISI canceler for N = 8, L = 2. . . 40 6.1 The normalized ICI waveform of observed subcarrier for the subcarrier

List of Tables

Chapter 1

Introduction

OFDM is an attractive technique for wireless communication, one of the main reasons is because OFDM effectively deals with the delay spread of the multipath channel by intro-ducing a cyclic prefix (CP) in every OFDM symbol. The length of CP must be longer than the maximum delay spread to assure the inter-symbol interference (ISI) and inter-carrier interference (ICI) are eliminated. However the use of CP result in a lowering of spectral efficiency. Especially when the OFDM systems are encountered to the multipath channels which has a very long delay spread. Increasing the length of the CP to reduce ISI actually has its limitations because it introduces a tremendous bandwidth penalty. In order to make full use of the bandwidth in OFDM systems, several approaches have been proposed to cope with this problem by shortening CP or removing entire CP.

An easy way is to increase the number of subcarrriers or the OFDM symbol duration so that the proportion of the CP can be reduced. But this method narrow the bandwidth of each subcarrier and makes OFDM systems more sensitive to the frequency offset and the time variant channel. The second way is to employ an iterative cancellation method known as the residual ISI cancellation (RISIC) to eliminate interference due to insuffcient CP [1]. The RISIC algorithm firstly removes ISI from a previous decoded OFDM block and restores the circulant structure of the channel iteratively. Many techniques based on RISIC have been proposed, whereas most of them offer good performance only when the length of channel impulse response (CIR) is moderate, which means the interference power is

much smaller than the signal power in these circumstances. Additionally, the RISIC is very sensitive to the effects of unideal ISI cancellation. The third way is to utilize time-domain or frequency-domain equalizer to combat the ISI and ICI [2][3][4][5]. The forth way aims to add redundancy by precoding techniques [6][7] or by the successive interference cancellation based on decision feedback structure [8] to mitigate ISI and ICI. Some of these schemes still require CP, and most of them don’t outperform the traditional OFDM systems with enough CP. Actually the ICI corrupted channel of the CP-reduced OFDM system can be viewed as a virtual MIMO channel when we regard the subcarriers as the virtual antennas. And the ICI induced by insufficient CP can be viewed as a sort of frequency diversity by the concepts of space-frequency coding (SFC). In other words, instead of eliminating the ICI as the previous studies proposed, we should preserve the ICI and make it a profitable factor for performance enhancement. For above observations, the demand for a carefully design of CP-reduced coding schemes based on OFDM systems to increase both spectral efficiency and error performance is required. In this thesis, we investigate the virtual space-frequency codes based on the effective MIMO channel of the CP-reduced OFDM system, and and propose the corresponding design criteria to develop good virtual space-frequency codes. The maximum achievable diversity order of the virtual space-frequency code is determined by the theoretical analysis. Simulation results are also provided to show that the proposed coding schemes not only achieve higher diversity order to enhance the error performance but also have higher data rate compared with the conventional coded OFDM systems. Note that timing and frequency synchronization are assumed to be perfect throughout this paper. The remainder of this thesis is organized as follows. In Chapter 2, an overview of the OFDM systems is given, and the mathematical formulations of equivalent ICI channel of CP-reduced OFDM systems after the ISI cancellation are introduced here. In Chapter 3, we give the reviews of the conventional space-time code (STC) and SFC, and we detail the derivation procedures of PEP. The design criteria and maximum achievable diversity order corresponding to STC and SFC are introduced as well. After the brief guild of the background knowledge, we derive the PEP of virtual space-frequency codes based the

effective MIMO channel of the CP-reduced OFDM systems in Chapter 4, and determine the corresponding maximum achievable diversity order by mathematical proofs. Before we leave Chapter 4, the design criteria good virtual space-frequency codes are proposed. Besides theoretical interpretation, we also carry out computer simulations in Chapter 5 for performance verifications. In Chapter 6, we summarize our investigations and propose some potential future works for performance optimization.

Chapter 2

Overview of OFDM systems

Orthogonal frequency division multiplexing (OFDM) modulation is a multi-carrier trans-mission technique that has been recently recognized as an excellent method for high speed bi-directional wireless data communication. OFDM modulation effectively squeezes multiple modulated carriers tightly together, reducing the required bandwidth but keeping the mod-ulated signals orthogonal so they do not interfere with each other. Furthermore, OFDM modulation divides the entire frequency selective fading channel into many narrow band flat fading subchannels in which high bit-rate data are transmitted in parallel and do not undergo inter-symbol interference due to the usage of cyclic prefix and long symbol dura-tion. Therefore, OFDM modulation has been chosen for many standards, including digital audio broadcasting (DAB), High Definition TV (HDTV), and wireless local area network (WLAN), . . . etc. Moreover, it is an important technique for high data-rate transmission over mobile wireless channels. In the following sections of this chapter , we introduce the basic concepts of OFDM modulation, and then give a brief introduction on the usage of cyclic prefix. As we known, OFDM systems with insufficient (length of cyclic prefix is shorter than maximum delay spread) cyclic prefix give raise to inter-symbol interference and inter-carrier interference, thus we introduce the mathematical models of inter-symbol interference and inter-carrier interference induced by using insufficient cyclic prefix before leaving this chapter.

2.1

System Model of OFDM Systems

Figure 2.1: System model of OFDM Systems.

Consider the base-band OFDM systems with N subcarriers as shown in Figure 2.1. The serial information data stream is mapped into constellation symbols by employing a general phase shift keying (PSK) modulation or quadrature amplitude modulation (QAM) scheme. The resulting symbol stream is demultiplexed into a vector of N data symbols to become the frequency-domain OFDM symbol {Xi,n}N −1_n=0, where Xi,n is the modulated

symbol on nth subcarrier of ith frequency-domain OFDM block. Next an inverse fast Fourier transform (IFFT)/fast Fourier transform (FFT) is used as a modulator/demodulator. For the ith transmission OFDM block, the N-point IFFT output sequence is

xi,k = 1 √ N N −1_X n=0 Xi,nexp ½ j2πnk N ¾ , k = 0, 1, . . . , N − 1, (2.1)

where {xi,k}N −1k=0 is the time-domain OFDM symbol and xi,k stands for the modulated symbol

on kth subcarrier of ith OFDM block. After the appending of cyclic prefix, the OFDM symbols are transmitted into the dispersive communication channels. The received OFDM symbols are weighted by the multipath fading gains and perturbed by the complex additive white Gaussian noise (AWGN) induced by the thermal noise. Next the receiver remove the cyclic prefix and employ an N-point FFT to get the frequency-domain received OFDM symbols. The recovered data symbols are demultiplexed in serial order and the demodulator maps received complex signals to the constellation points which has the most likely. The

demodulation is performed over all subcarriers of OFDM symbols, then we have the decoded data stream stream of one transmission.

2.2

Cyclic Prefix, symbol Interference and

Inter-carrier Interference

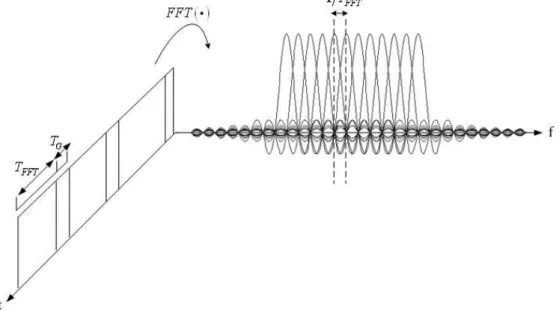
Due to the delay spread nature of the multipath channels, previous OFDM blocks are overlapped to next OFDM blocks and cause inter-symbol interference (ISI) among consec-utive OFDM blocks. An easy design for avoiding ISI is to insert a replica of OFDM symbol in front of itself, which is the cyclic prefix (CP) [9][10]. Assumed the subcarrier numbers is N, the length of CP is G, The CP is conventionally chosen as the last sample points of each time-domain OFDM symbol just like the idea depicted in Figure 2.2. And the

Figure 2.2: Stylized plot of time-domain OFDM symbol with CP of G samples.

(a) CP-OFDM with sufficient CP (b) CP-OFDM with insufficient CP

Figure 2.3: (a) CP-OFDM with sufficient CP, (b) CP-OFDM with insufficient CP CP must be longer or at least equals to the order of the maximum delay spread of the multipath channels to guarantee the OFDM system is ISI-free. Later, we assuming the maximum delay spread is no longer than one OFDM duration, and detail the concepts of ISI and ICI induced by insufficient CP. As shown in Figure 2.3(a), since the CP length G is not smaller than maximum delay spread L, the ith received time-domain OFDM block

overlaps with two signal components at the receiver, one is the CP part of itself and the other is (i − 1)th received OFDM block. Due to the orthogonality of the subcarriers, the time-domain OFDM symbols overlap with CP of themself is not harmful. And the receiver discards the CP of ith OFDM block before signal detection, therefore the ISI induced by previous OFDM block is completely deleted. Therefore by appending sufficient length of CP, the ISI problem is simply solved, and the time-domain OFDM symbols are superposed to each other at the CP part with their frequency-domain symbols being perpendicular to each other, just like the stylized plots of CP-sufficient OFDM symbols in time-domain and frequency-domain shown in Figure 2.4. For the case of L > G as shown in Figure 2.3(b),

Figure 2.4: Stylized plot of the time-domain and frequency-domain OFDM symbols with sufficient CP.

the ith received OFDM block overlaps with last L − G sample points of (i − 1)th OFDM block, and the received data on each subcarrier of ith OFDM block is perturbed by received data of (i − 1)th’s, end up causing the degradation of error performance.

After the conceptual guide of CP and ISI, next we introduce the channel matrices of ISI and ICI induced by insufficient CP from analytical point of view. The received signals of CP-reduced OFDM symbols can be always divided into three parts: the received OFDM symbol without ISI and ICI (which is the interference-free components), the ISI contribution from

the previous symbol due to insufficient CP, and the ICI contribution caused by insufficient CP. To be more clear, when G < L, the OFDM systems undergo ISI and ICI, and the received OFDM symbols can be viewed as an interference-free received OFDM symbol (just like the received OFDM symbol of CP-sufficient case) minus the ICI contributed by the insufficient CP parts of the OFDM symbols and add the ISI contribution from the previous OFDM block [11]. If G ≥ L, the ISI and ICI contributions are both zero. Now, assuming the channel is static for at least one OFDM duration, and the ith time-domain transmit/receive OFDM block are denoted by r(i) _{and X}(i)_{, the mathematical representation of ith received}

OFDM block is given by

r(i) _{= H}(i)_X(i)

| {z } Interference-free

+ H(i)_isiX(i−1)

| {z } ISI

− H(i)_iciX(i)

| {z } ICI

. (2.2) If we denote the multipath channel gains during ith OFDM block as h(i)_l , l = 0, 1, . . . , L, the

ith received inference-free OFDM block can be formulated into a matrix form of H(i)_X(i)

with H(i) _{is given by}

H(i) ₌                   

h(i)₀ 0 . . . 0 h(i)_L . . . h(i)₂ h(i)₁ h(i)₁ h(i)₀ 0 . . . 0 h(i)_L . . . h(i)₂

... . .. ... ... ... ... ... ...

h(i)_L−1 . .. ... h(i)₀ 0 . .. ... h(i)_L

h(i)_L h(i)_L−1 . .. ... ... ... ... 0

0 h(i)_L . .. ... ... ... ... ...

... . .. ... ... ... ... h(i) 0 0

0 . . . 0 h(i)_L h(i)_L−1 . . . h(i)₁ h(i)₀

                   . (2.3)

Since H(i)_{has a circulant structure in (2.3), H}(i)_{can be diagonalized by N-point FFT matrix}

and IFFT matrix, which dramatically simplify the complexity of the channel equalizer. Thus if the length of CP is sufficient, the receiver can use a single weighted frequency-domain equalizer (1-tap FEQ) to compensate the multipath channel response. For the ISI signal

component induced by insufficient CP, the time-domain ISI channel matrices are H(i)_isi=              0 . . . 0 h(i)_L . . . h(i)₁ ... ... ... ... ... ... ... ... ... ... 0 h(i) L ... ... ... ... ... 0 0 . . . ... ... ... ... 0 . . . 0 . . . . 0              . (2.4)

The time-domain ICI component is induced by subtracting the contribution of the unused CP parts of the OFDM symbols. Therefore the time-domain ICI channel matrix is the column-wise left shift version of the non-zero parts of the time-domain ISI channel matrix by G times. And the time-domain ICI channel matrix is given by

H(i)_ici = H(i)_isi 

 0G×(N −G) IG×G

I(N −G)×(N −G) 0(N −G)×G



 _(2.5) where the 0 and I in (2.5) are the all zero matrix and the identity matrix with matrix size specified by their subscripts. We can get the frequency-domain of CP-sufficient, ISI and ICI channel matrix by simply left multiply the IFFT matrix and right multiply the FFT matrix to each of the aforementioned channel matrices (2.3), (2.4), and (2.5).

Chapter 3

Reviews of Space-Time Coding and

Space-Frequency Coding

Two of the major impairments of wireless communications systems are fading caused by destructive addition of multipaths in the propagation medium and interference from other users. Severe anttenuation makes it impossible for the receiver to determine the trans-mitted signal unless some less-attenuated replica of the transtrans-mitted signal is provided to the receiver. This resource is called diversity. In 1998, a communication technique called space-time coding (STC) scheme which utilizes diversity to combat fading and interference is firstly proposed by Tarokh, Seshadri,and Calderbank [12][13]. The space-time coding introduces temporal and spatial correlation into the transmitted signals, so as to achieve transmit diversity as well as a coding gain without sacrificing the bandwidth. Moreover, it is an effective way to approach the capacity of multiple-input multiple-output (MIMO) wire-less channels. Inspired by STC, space frequency coding (SFC) scheme which extends the diversity technique to multi-carrier systems operating over broadband channels is developed by Bolcskei and Paulraj in 2000 [14]. Bolcskei and Paulraj found out that the STC systems designed to achieve full spatial diversity in the narrowband case is in general not yielding full space-frequency diversity, therefore the space-frequency coding scheme across frequency and spatial domain to achieve not only spatial diversity but frequency diversity was inves-tigated. There are variety of STC systems with respect to distinct coding schemes, such as, space-time block coding [15][16], space-time trellis coding [17][18], space-time frequency

coding [19][20], unitary space-time modulation [21][22], space-time turbo trellis coding [23], differential space-time coding [24][25], and layered space-time coding [26][27], . . . etc. In the following sections of this chapter, we will focus on the encoding and decoding schemes of STC and SFC along with their design criteria over quasi-static fading channels.

3.1

Space-Time coding

3.1.1

System Model of STC

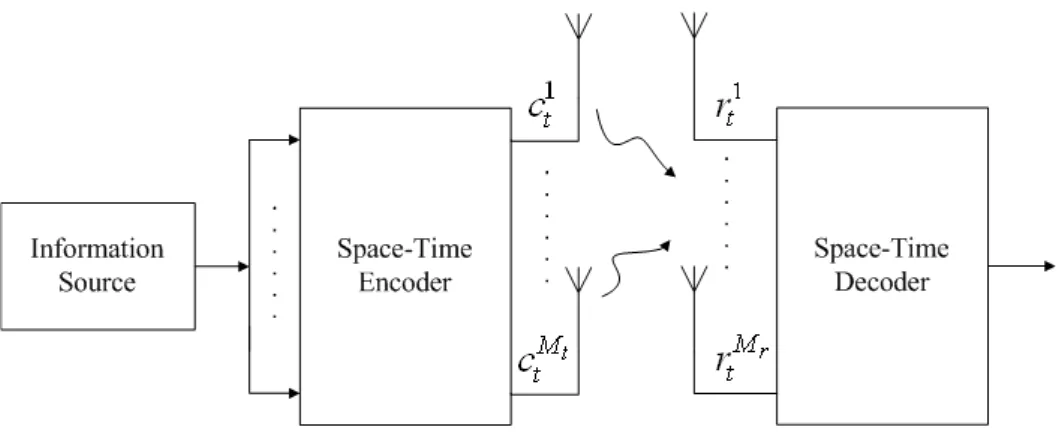
Consider a MIMO system with MT transmit antennas and MR receive antennas as shown

in Figure 3.1. After encoding, the MT antennas simultaneously transmit the encoded data

into the communication channel. At the receiver, the transmission signals of different trans-mit antennas undergo channel fading and then superpose to each other along with the thermal noise at the receive antennas. Assume wireless channels are quasi-static fading and memoryless, the received signal of antenna q at time t is given by

r_tq = MT X p=1 hq,p p Escpt + ztq, q = 1, 2, . . . , MR, t = 1, 2, . . . , L, (3.1)

where cp_t with energy √Es is the coded symbol transmitted by pth antenna at time t.

Channel fading gains for the path from transmit antenna i to receive antenna j are denoted as hq,p, and they are assumed to be independent complex Gaussian random variables with

mean mq,p_h and variance 0.5 per dimension. z_tq stands for the thermal noise of qth antenna at time t, and z_tq are also independent Gaussian distribution with zero mean and one-side power spectral density of N0.

3.1.2

Design Criteria of STC

The pairwise error probability (PEP), P (c, ˆc) is the probability that decoder selects an erroneous sequence ˆc = ˆcq_t, (∀q, t), when the transmitted sequence was in fact c = cq_t, (∀q, t).

Assume the receiver has perfect channel state information (CSI), and the decoder performs maximum likelihood (ML) decoding to recover signals. The PEP with respect to (3.1) is

Figure 3.1: System model of STC. given by Pr (c → ˆc|hq,p, ∀ p, q, t) = Pr  XL t=1 MR X q=1 ¯ ¯ ¯ ¯ ¯r q t − MT X p=1 hq,p p Escpt ¯ ¯ ¯ ¯ ¯ 2 ≥ L X t=1 MR X q=1 ¯ ¯ ¯ ¯ ¯r q t − MT X p=1 hq,p p Esˆcpt ¯ ¯ ¯ ¯ ¯ 2  = Pr   L X t=1 MR X q=1 2Re ( z_tq MT X p=1 hq,p p Es(cpt − ˆcpt) ) ≥ L X t=1 MR X q=1 ¯ ¯ ¯ ¯ ¯ MT X p=1 hq,p p Es(cpt − ˆcpt) ¯ ¯ ¯ ¯ ¯ 2  = Q Ãr d2_{(c, ˆc)} Es 2N0 ! ≤ 1 2exp µ −d2(c, ˆc) Es 4N0 ¶ (3.2) where Q(x) is the complementary error function defined by

Q (x) = √1

2π Z _∞

x

exp¡−x2_/2¢_{dx (3.3)}

and the modified Euclidean distance is denoted as

d2_{(c, ˆc) =} L X t=1 MR X q=1 ¯ ¯ ¯ ¯ ¯ MT X p=1 hq,p(cpt − ˆcpt) ¯ ¯ ¯ ¯ ¯ 2 . (3.4)

Define hq= (hq,1, hq,2, . . . , hq,MT), we can rewrite (3.4) in matrix form, we have

d2_{(c, ˆc) =} MR X q=1 hqB(c, ˆc)B (c, ˆc)HhHq = MR X q=1 hqA(c, ˆc)hHq (3.5)

where B(c, ˆc) is the codeword difference matrix defined as B (c, ˆc) =        c1 1− ˆc11 c12− ˆc12 · · · c1L− ˆc1L c2 1− ˆc21 c22− ˆc22 · · · c2L− ˆc2L ... ... . .. ... cMT 1 − ˆcM1 T cM2 T − ˆc2MT · · · cMLT − ˆcMLT        (3.6)

and the codeword distance matrix is defined as A (c, ˆc) = B (c, ˆc) B (c, ˆc)H. Note that A (c, ˆc) is nonnegative definite matrix, thus we can decompose A (c, ˆc) as

UA (c, ˆc) UH _{= D (3.7)}

where U is an unitary matrix with its column vectors being eigenvectors of A (c, ˆc) and D is a diagonal matrix with its diagonal elements λp, p = 0, 1, . . . , MT, being nonnegative

eigenvalues of A (c, ˆc). Now, (3.5) can be rewritten as

d2(c, ˆc) = MR X q=1 MT X p=1 λp, |βq,p|2, (3.8) where βq,p = hq· up (3.9)

and up is the pth row of U. Substituting (3.8) into (3.2), we get

Pr (c → ˆc|hq,p, ∀ p, q) ≤ 1 2exp à − Es 4N0 MR X q=1 MT X p=1 λp|βq,p|2 ! . (3.10) We average the conditional PEP over all channel realization to get pairwise error prob-ability. First of all, βq,p are obviously independent complex Gaussian random variables

with mean µq,p and variance 0.5 per dimension, therefore |βq,p| are Rician distribution. The

probability density function of Rician random variable is

f (|βq,p|) = 2 |βq,p| exp ¡ − |βq,p|2− κq,p ¢ I0 ¡ 2 |βq,p|√κq,p ¢ (3.11) where κq,p = |µβ,p,q|2, µi,q = E[hq· up] and I0(·) represents the zero-order modified Bessel

pairwise error probability can be expressed as Pr (c → ˆc) = Z _∞ 0 · · · Z _∞ 0 Pr (c → ˆc|βq,p , ∀p, q)f (|β1,1|) f (|β1,2|) · · · f (|βMR,MT|) d |β1,1| d |β1,2| · · · d |βMR,MT| ≤ Z _∞ 0 · · · Z _∞ 0 1 2exp à − Es 4N0 MR X q=1 MT X p=1 λp|βq,p|2 ! f (|β1,1|) f (|β1,2|) · · · f (|βMR,MT|) d |β1,1| d |β1,2| · · · d |βMR,MT| ≤ 1 2 MR Y q=1 à _r Y p=1 1 1 + Es 4N0λp exp à −κq,p Es 4N0λp 1 + Es 4N0λp !! (3.12) where r(·) stands for rank of A (c, ˆc). Consider the wireless channel to be Rayleigh fading, that is, µβ,q,p = 0, the PEP can be upper bounded as

Pr (c → ˆc) ≤ 1₂ Ã r Y p=1 1 1 + Es 4N0λp !_MR . (3.13) At high SNR’s, (3.13) can be represented as

Pr (c → ˆc) ≤ 1₂ Ã r Y p=1 λp !_−MRµ Es 4N0 ¶_−rMR . (3.14) As a consequence, we have the design criteria of space time coding as follows.

• Rank (diversity) criterion: The minimum rank of A (c, ˆc) over all pairs of distinct

codewords c and ˆc should be as large as possible.

• Determinant criterion: The minimum product of nonzero eigenvalues Qr

p=1

λp over all

pairs of distinct codewords c and ˆc should also be maximized.

The rank and determinant criteria give us a guild line to develop good space time codes, and the maximum achievable diversity of space time codes is the multiplication of encoding durations and received antenna numbers, i.e. LMR.

3.2

Space-Frequency coding

The STC systems introduced in previous section is restricted to single-carrier systems operating narrow-band flat fading channels. A strategy which employing STC across OFDM

tones over MIMO broad-band channels to provide not only spatial diversity but frequency diversity was investigated, that is, the space-frequency coding. The design criteria of SFC are introduced in the following.

3.2.1

System Model of SFC

Figure 3.2: System model of SFC.

The MIMO-OFDM system equipped MT transmit antennas and MRreceive antennas

is showned in Figure 3.2. The information bits are encoded by the SFC encoder into blocks of size MT × N, and the coded symbol is fed to the OFDM modulator to perform

IFFT transform and append the cyclic prefix. And then the time-domain OFDM symbols are transmitted into the MIMO channels. At receiver, the transmitted signals of all the transmit antennas are weighted superposition and currupted by AWGN at each receive antenna. Organizing the transmitted data symbols of kth subcarrier into frequency vectors ck = ¡ c0 k, c1k, . . . , cMkT−1 ¢T with ci

k denoting the data symbol transmitted from the ith

antenna on the kth tone and ci

k are taken from a finite complex alphabet such that the

average energy of the constellation element is Es, then the received data vector of the kth

tone is given by rk = p EsH ³ ej2πkN ´ ck+ nk, k = 0, 1, . . . , N − 1, (3.15) where H ³ ej2πk N ´

is the frequency domain channel matrix. And nk is independent complex

AWGN with mean zero, variance 0.5 per dimension and one sided power spectral density

3.2.2

Design Criteria of SFC

Assuming the channel is constant over at least one OFDM symbol, and the perfect CSI is available at the receiver. The ML decoder decides the most likely transmitted sequence ˆck, k = 0, 1, . . . , N − 1, over all possible codewords according to

ˆ ck = argCmin N −1 X k=0 ° ° °rk− p EsH ³ ej2πkN ´ ck ° ° °2 (3.16) where C = [c0c1 . . . , cN −1]. Let E = [e0e1 . . . , eN −1] be the erroneous decode

space-frequency codeword, for a given channel realization, the pairwise error probability is given by P ³ C → E|H ³ ej2πk N ´´ = Q Ãr Es 2N0 d2 ³ C, E|H ³ ej2πk_N ´´ ! (3.17) where the squared Euclidean distance between the two codewords C and E is dented by

d2³_{C, E|H}³_ej2πk N ´´ = N −1_X k=0 ° ° °H ³ ej2πk N ´ (ck− ek) ° ° °2 = kYk2. (3.18) Here we define a new matrix Y = [y0, y1, . . . , yN −1]T in equation (3.18) for computational

convenience, and the definition of yk, k = 0, 1, . . . , N − 1, is given by

yk= H ³ ej2πk N ´ (ck− ek) . (3.19)

Using the Chernoff bound Q(x) ≤ e−x2_/2

into equation (3.17), we get P ³ C → E|H ³ ej2πk N ´´ ≤ e4N0Es d2 µ C,E|H µ ej 2πkN ¶¶ . (3.20) Since the multipath channel were assumed to be i.i.d. complex Gaussian it follows that H³ej2πk

N

´

are Gaussian as well and hence the vector Y is Gaussian. The average over all channel realizations of the right handside in (3.20) is equivalent to solving the characteristic function of Y and it is fully characterized by the eigenvalues of the covariance matrix of Y [28]. Therefore the pairwise error probability is given by

P (C → E) ≤ r(CYY)−1µ 1 + λi(CY) Es 4N0 ¶₋₁ (3.21)

where r (CY) denotes the rank of CY , λi(CY) , i = 0, 1, . . . , r (CY) , are the nonzero

eigenvalues of CY, the definition of CY is given by

CY = E £ YYH¤ = L−1 X l=0 h Dl_{(C − E)}T _{(C − E)}∗¡_Dl¢Hi_{⊗ R} l (3.22) where D = diag{e−j2πk N }N −1

k=0 , Rl denote the correlation matrix of MIMO channel between

transmit and receive antennas at time delay l, A ⊗ B denotes the Kronecker product of the matrices A and B, and the superscript ∗ stands for complex conjugate operation. Assume the SFC systems are operated at high SNR, the PEP can be upper bounded by

P (C → E) ≤   r(CYY)−1 i=0 λi(CY)   µ Es 4N0 ¶_−r(CY) . (3.23) The design criteria for space-frequency codes follow from equation (3.23) as the well-known rank and determinant criteria.

• Rank (diversity) criterion: The minimum rank of CY over all pairs of distinct codewords

C and E should be as large as possible.

• Determinant criterion: The minimum product of nonzero eigenvaluesr(CQY)

i=0

λi(CY) over

all pairs of distinct codewords C and E should also be maximized.

Next, we shortly introduce the maximum achievable diversity of the space-frequency codes by the discussion of CY. Assume N > MTL, using the factorizations of Rl =

R12

l R

1 2

l , l = 0, 1, . . . , L − 1, and the property of Kronecker products

(A ⊗ B) ⊗ (C ⊗ D) = (AC) ⊗ (BD) (3.24) the NMR× MTMRL matrix CY can be decomposed as

CY = G (C, E) GH(C, E) (3.25)

where G (C, E) is defined as G (C, E) = [g0g1 . . . gL−1] and gl=

h³

Dl_{(C − E)}T´_{⊗ R}12

l

i .

If the MIMO channels satisfy the condition of r (Rl) = MR and by carefully design of

space-frequency codeword to have r ³

Dl_{(C − E)}T´_{= M}

T for all l over all distinct codeword

pairs, the stacked matrix G (C, E) would be full rank. As above conditions are fulfilled, we thus have a full rank CY and the space-frequency codes can achieve the maximum diversity

Chapter 4

CP-reduced Coding Techniques with

ICI Diversity Combining for OFDM

Systems

Actually the ICI corrupted channel of the CP-reduced OFDM system can be viewed as a virtual MIMO channel when we regard the subcarriers as the virtual antennas. And the ICI induced by insufficient CP can be viewed as a sort of frequency diversity by the concepts of space-frequency coding (SFC). In this chapter, we study the space-frequency codes under the virtual MIMO channel of CP-reduced OFDM systems, and we term such codes as “virtual

space-frequency codes”. The maximum achievable diversity order and the corresponding

design criteria are also given by theoretical analysis of the derived PEP bound.

4.1

System Model of OFDM Systems

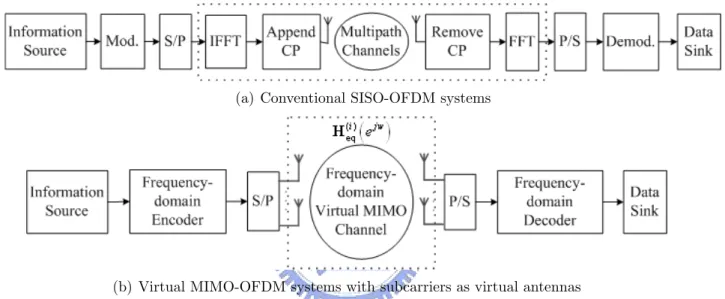
If we view the subcarriers as the virtual antennas, and combine the system blocks circled by dash lines in Figure 4.1(a) into a equivalent frequency-domain MIMO channels as shown in Figure 4.1(b) emphasized by dash lines, then conventional CP-reduced SISO-OFDM systems with perfect ISI canceller can be regarded as virtual MIMO-OFDM systems with their virtual MIMO channels of ith OFDM block index are specified by the frequency-domain ICI channels of H(i) eq ¡ ejw¢_{= F} N ³ H(i)_{− H}(i) ici ´ FH N, (4.1)

where FN is the N-point FFT matrix, H(i) and H(i)ici are the time-domain channel matrices

in (2.3), and (2.5) which are the channel matrices corresponding to interference-free and ICI signal components. Under the aspects of subcarriers as virtual antennas and following the concepts of SFC, the ICI induced from reduced CP can equivalently be considered as the virtual MIMO channel gains from virtual transmit antennas to virtual received antennas. That is, ICI can be regarded as frequency diversity. After a clear understanding of the virtual spatial-domain, next we derive the PEP based on the virtual MIMO-OFDM systems shown in Figure 4.1(b).

(a) Conventional SISO-OFDM systems

(b) Virtual MIMO-OFDM systems with subcarriers as virtual antennas

Figure 4.1: (a) Conventional SISO-OFDM Systems, (b) Virtual MIMO-OFDM with sub-carriers as virtual antennas

4.2

Pairwise Error Probability Analysis

From the viewpoints of regarding subcarriers as virtual antennas, we investigate a coding technique across B OFDM blocks based on the concepts of SFC for the virtual MIMO-OFDM systems with perfect ISI canceller. Assume the channel responses are static at least for one OFDM duration (symbol-wise fading), and the channel gains for different delay are independent. The input bit stream is divided into b bit-long segments, forming 2b_{-ary constellation symbols. These symbols are then mapped onto a frequency-domain}

codeword to be transmitted over the N virtual antennas (subcarriers). Each frequency-domain codeword can be express as an NB × 1 matrix

X =£XT

1, XT2, . . . , XTB

¤_T

(4.2) where Xi = [xi,0, xi,1, , · · · , xi,N −1] is an N × 1 column vector, representing the ith coded

OFDM block. At the receiver, the received signal of ith block can be written in matrix form as Ri = p EsH(i)eq ¡ ejw¢Xi+ ZTi , (4.3)

where the complex additive white Gaussian noise (AWGN) vector of ith block index is defined as Zi = [zi,0, zi,1, . . . , zi,N −1], and zi,j ∼ CN (0, N0) is the complex AWGN of

ith OFDM block at j subcarrier. Thus the average coded symbol to noise ratio at each

subcarrier is given by Es/N0. Collect B blocks of received OFDM signals and denote

R =£RT

1, RT2, . . . , RTB

¤_T

, then R is an NB × 1 column vector, and is given by R =pEsHeq

¡

ejw¢X + Z, (4.4) where the noise vector Z is formatted as Z = £ZT

1, ZT2, . . . , ZTB

¤_T

, and Heq(ejw) is the

virtual MIMO channel matrix in frequency-domain of consecutive B OFDM blocks, and can be formulated as Heq ¡ ejw¢=         h H(1)eq (ejw) i h H(2)eq (ejw) i . .. h H(B)eq (ejw) i         . (4.5)

Assume perfect channel state information (CSI) is available at the receiver, and the receiver applies a maximum likelihood decoder to detect signals. The PEP of coding across consecutive B OFDM blocks conditioned on the virtual MIMO channels of Heq(ejw) is given

by P ³ X, ˆX¯¯Heq ¡ ejw¢´_{= Q}     v u u td2H ³ X, ˆX ´ 2N0     , (4.6)

where ˆX stands for the erroneous decoded codeword, Q (x) is the complementary error function, and d2

H(X, ˆX) is the modified Euclidean distance with the definition of d2 H ³ X, ˆX´ = ° ° °Heq(ejw) ³ X − ˆX´°°°2 F = PB i=1 ° ° °H(i)eq (ejw) ³ Xi− ˆXi ´°_° °2 F. (4.7) By using the Chernoff bound, the conditional PEP can be upper bounded by

P ³ X, ˆX¯¯Heq ¡ ejw¢´≤ 1 2exp µ −ES 4N0 d2_H ³ X, ˆX ´¶ . (4.8) Next we rewrite d2

H(X, ˆX) into a more compact form for computational simplicity of channel

averaging. By the equalities of tr¡AAH¢ _{= kAk}2

F and tr (AB) = vec

¡ AH¢H_{vec (B) [29],} we can reformulated (4.7) as d2 H(X, ˆX) = B X i=1 vec ³ Ai ³ X, ˆX ´ H(i) eq ¡ ejw¢H´H_vec³_H(i) eq ¡ ejw¢H´_{, (4.9)}

where Ai(X, ˆX) = (Xi− ˆXi)(Xi− ˆXi)H is the ith codeword distance matrix, and vec(·)

is an operator that stacks all the columns of a matrix into a super column matrix orderly according to their column indexes. Apply the equality of vec (ABC) = ¡CT _{⊗ A}¢_{vec (B)}

[29], (4.9) becomes d2 H ³ X, ˆX ´ = B X i=1 vec ³ H(i) eq ¡ ejw¢H´H³_I N ⊗ Ai ³ X, ˆX ´´ vec ³ H(i) eq ¡ ejw¢H´_{. (4.10)} Define hi = vec ³ H(i)eq (ejw)H ´

and Ki(X, ˆX) = IN ⊗ Ai(X, ˆX), the modified Euclidean

distance is then given by

d2 H ³ X, ˆX ´ = B X i=1 hH i Ki ³ X, ˆX ´ hi. (4.11)

Now we are about to average the conditional PEP over all channel realization, but we can’t assure if the random vector hi has a full rank covariance matrix for each i (actually hi

has a rank-deficient covariance matrix for each i, and its proof is shown in the appendix). Therefore, to ease the calculation of integral during the step of channel averaging, we con-sider a linear transformation to transform h into a random vector with a full rank covariance

to simplify the computation of integral. Assume hi is a complex Gaussian random vector

with its mean denoted by µh and covariance denoted by Rh with rank(Rh) = r ≤ N2.

Consider the linear transformation of the ith channel vector hi = µh+ R 1 2 hgi, (4.12) where gi ∼ CN (0, Ir) and R 1 2

h stands for the Cholesky decomposition of the covariance

matrix Rh [30]. By this transformation, we can transform each hi to another random

vector gi which has zero mean and an identity covariance matrix. Substitute (4.12) into

(4.11), then the modified Euclidean distance can be finally formulated as

d2 H ³ X, ˆX ´ = PB i=1 ³ µh+ R 1 2 hgi ´_H Ki ³ X, ˆX ´ ³ µh+ R 1 2 hgi ´ = PB i=1 d2 Hi ³ X, ˆX´. (4.13) Now we average the conditional PEP over all channel realizations

P ³ X, ˆX ´ ≤ QB i=1 R gi ¡₁ πr ¢ exp ³ − ³ Es 4N0 ´ d2 Hi ³ X, ˆX ´´ exp¡−gH i gi ¢ dgi ≤ QB i=1 µ det µ Ir+ ³ Es 4N0 ´ ³ R12 h ´H Ki ³ X, ˆX ´ R12 h ¶¶₋₁ exp ³ − ³ Es 4N0 ´ µH hKi ³ X, ˆX ´ µh ´ · exp à ³ Es 4N0 ´₂ ΦH · Ir+ ³ Es 4N0 ´ ³ R12 h ´H Ki ³ X, ˆX ´ R12 h ¸₋₁ Φ ! , (4.14) where Φ = ³R12 h ´H

Ki(X, ˆX)µh. Consider the multipath channels to be Rayleigh fading

channels (i.e. µh= 0), and after some computations, the PEP can be upper bounded by

P ³ X, ˆX ´ ≤ B Y i=1 µ det µ Ir+ µ Es 4N0 ¶ K(i)_{ef f} ³ X, ˆX ´¶¶−1 , (4.15) where K(i)_{ef f}(X, ˆX) is the effective codeword matrix of ith OFDM block, and is defined as

K(i)_{ef f} ³ X, ˆX ´ = ³ R12 h ´H Ki ³ X, ˆX ´ R12 h. (4.16)

Here we use the phase “effective” to emphasize K(i)_{ef f}(X, ˆX) is a codeword distance matrix that not only depends on the codeword distance matrix Ai(X, ˆX), but also depends on the

covariance matrix of the multipath channels. Note that K(i)_{ef f}(X, ˆX) is nonnegative definite Hermitian, thus there exists a unitary matrix Ui and a real diagonal matrix Di such that

Ui ·³ R12 h ´H Ki ³ X, ˆX ´ R12 hi ¸ UH_i = Di, (4.17)

where the rows of Ui are the eigenvectors of K(i)ef f(X, ˆX), forming a complete orthonormal

basis of an N2_{-dimensional vector space. The diagonal matrix D}

i can be represented as Di =     λ(i)₁ . .. λ(i)_Ri     (4.18)

where R(i)_i stands for the rank of K(i)_{ef f}(X, ˆX), and λ(i)_j , j = 0, . . . , Ri, i = 1, . . . , B are

the nonzero eigenvalues of K(i)_{ef f}(X, ˆX). At high SNR’s, the upper bound of PEP can be simplified as P ³ X, ˆX ´ ≤ Ã B Q i=1 Ri Q j=1 λ(i)_j !₋₁ ³ Es 4N0 ´_−PB i=1 Ri (4.19) or P ³ X, ˆX ´ ≤ ³ det ³ Kef f ³ X, ˆX ´´´₋₁³ Es 4N0 ´_{−rank(Kef f(X, ˆX))} , (4.20)

here we further define a total effective codeword distance matrix with its definition is given by Kef f ³ X, ˆX ´ =         h K(1)_{ef f} ³ X, ˆX ´i h K(2)_{ef f} ³ X, ˆX ´i . .. h K(B)_{ef f} ³ X, ˆX ´i         . (4.21)

Based on the upper bounds shown in (4.19) and (4.20), we have the insights on the factors that determine the diversity order and coding gain of system performance, and we can tell that both diversity and coding gains are closely related to the total effective codeword distance matrix. Thus we give a proof of the achievable diversity order along with detail discussions in next section.

4.3

Maximum Achievable Diversity and Design

Crite-ria

We analyze the factors that affect the diversity order of a SF-coded virtual MIMO-OFDM system in this section. First, we derive an upper bound for the maximum achievable diversity for such a system. Second, we propose the design criteria according to the derivation results of the upper bound of maximum achievable diversity. From the PEP in (4.19) and (4.20), we can see that the diversity order is determined by the rank of the total effective distance matrix Kef f(X, ˆX), and Kef f(X, ˆX) depends on K(i)ef f(X, ˆX), for i = 1, . . . , B. Therefore,

in order to determine the upper bound of rank(Kef f(X, ˆX)), we should firstly determine

the upper bound of rank ³

K(i)_{ef f}(X, ˆX) ´

, and then applying the upper bound to determine the rank of Kef f(X, ˆX). The upper bound of rank

³

K(i)_{ef f}(X, ˆX) ´

and rank(Kef f(X, ˆX))

can be calculated in the following theorem.

Theorem 1. Consider a coding scheme based on CP-reduced OFDM systems under symbol-wise Rayleigh fading channels for a given subcarrier number N and channel order (L + 1), the maximum achievable diversity order is given by:

(1.a) If N ≥ (L+1) and K(i)_{ef f}(X, ˆX) 6= 0 for ∀X 6= ˆX in ith OFDM block, then rank ³

K(i)_{ef f}(X, ˆX) ´

≤

(L + 1) and therefore the rank of the coded B OFDM blocks are upper bounded by

rank(Kef f(X, ˆX)) ≤ N × (L + 1) .

(1.b) If N < (L+1) and K(i)_{ef f}(X, ˆX) 6= 0 for ∀X 6= ˆX in ith OFDM block, then rank³K(i)_{ef f}(X, ˆX)´≤

N × rank(Ai(X, ˆX)) and therefore the the rank of the coded B OFDM blocks are upper

bounded by rank(Kef f(X, ˆX)) ≤ N × B

P

i=1

rank(Ai(X, ˆX)).

Proof. By equation (4.16) and the inequality of rank(AB) ≤ min {rank(A), rank(B)},

then the upper bound of rank ³ K(i)_{ef f}(X, ˆX) ´ is given by rank ³ K(i)_{ef f}(X, ˆX) ´ ≤ min ³ rank ³ R12 h ´ , rank ³ Ki(X, ˆX) ´´ . (4.22)

Therefore we analyze the rank of R12

h and Ki(X, ˆX) individually to determine which matrix

has the minimum rank that upper bounds the diversity order. We deal with Ki(X, ˆX) first.

Using the fact that each eigenvalue of the N × N matrix Ai(X, ˆX) is an eigenvalue of the N2_{× N}2 _{matrix I}

N ⊗ Ai(X, ˆX) with multiplicity N, thus the rank of Ki(X, ˆX) is given by rank ³ K(i) ³ X, ˆX ´´ =    N × rank(Ai(X, ˆX)) , ifAi(X, ˆX) 6= 0. 0 , ifAi(X, ˆX) = 0. (4.23) From (4.23) we can conclude that only if the ith codeword distance matrix Ai(X, ˆX) is

nonzero for all pairs of ith distinct OFDM symbols, then rank(Ki(X, ˆX)) will be the

mul-tiplication of rank(Ai(X, ˆX)) and subcarrier number N.

The rank of R12

h is equivalent to the rank of rank (Rh), therefore we calculate rank (Rh)

in the following. By the equality of vec (ABC) = ¡CT _{⊗ A}¢_{vec (B), R}

h can be rewritten as Rh = ¡ F∗_N ⊗ FH_N¢Φ¡F∗_N ⊗ FH_N¢H (4.24) where Φ = E£ηηH¤ (4.25) and η = vec µ³ H(i)_{− H}(i) ici ´_H¶ (4.26) in which E[·] stands for taking expectation and “∗” stands for the complex conjugate op-erator. Using the inequality rank(AB) ≤ min {rank(A), rank(B)} again, then rank (Rh)

can be upper bounded by

rank (Rh) ≤ min ¡ rank¡F∗ N ⊗ FHN ¢ , rank (Φ)¢. (4.27)

Note that the FFT matrix FN is a full rank matrix so we have rank

¡ F∗

N ⊗ FHN

¢

= N2 _by

the rank property of kronecker product. Thus rank (Rh) is always upper bounded by

Now we shall determine rank (Φ) to determine the exact value of the upper bound of

rank (Rh). Because the channel taps are assumed to be independent, the equality

rank (Φ) = L + 1 (4.29)

always holds†_{. Therefore rank (R}

h) is always upper bounded by the channel order of (L + 1),

that is,

rank (Rh) ≤ (L + 1) . (4.30)

The rank of K(i)_{ef f}(X, ˆX) is upper bounded by the minor value of rank(Ki(X, ˆX)) and

rank (Rh) which means the upper bound of rank

³

K(i)_{ef f}(X, ˆX) ´

for any one-to-one map-ping coding scheme is either N × rank(Ai(X, ˆX)) or the channel order (L + 1).

There-fore we can conclude that rank ³

K(i)_{ef f}(X, ˆX) ´

≤ (L + 1) holds for N ≥ (L + 1), and rank

³

K(i)_{ef f}(X, ˆX) ´

≤ N × rank(Ai(X, ˆX)) holds for N < (L + 1). Note that the total

effective codeword distance matrix Kef f(X, ˆX) is formed by placing 1th to Bth effective

distance codeword matrix orderly at its diagonal and by the aforementioned maximum achievable diversity order of any one-to-one mapping coding schemes within one OFDM block, thus the maximum achievable diversity order of any one-to-one mapping coding schemes for consecutive B OFDM blocks is the cumulation of maximum achievable diver-sity order of each block index, i.e. rank(Kef f(X, ˆX)) ≤ N × (L + 1) for N ≥ (L + 1) and

rank(Kef f(X, ˆX)) ≤ N ×

B

P

i=1

rank(Ai(X, ˆX)) for N < (L + 1).

As shown in Theorem (1.a), when N ≥ (L + 1), a one-to-one mapping coding scheme within one OFDM block can always achieves (L + 1)-fold diversity, which means the vir-tual space-frequency code design based on CP-reduced OFDM systems under symbol-wise Rayleigh fading channels is no longer focusing on maximizing the diversity order since the full diversity can be always achieved only if the codes is designed to be one-to-one mapping. And the maximum achievable diversity order in this setup is consistent with the maximum achievable diversity of conventional SFCs under the case of single transmit and receive an-tenna. On the other hand, if N < (L + 1), the diversity order of a one-to-one mapping

coding scheme within one OFDM block can achieve N × rank(Ai(X, ˆX))-fold diversity as

shown in Theorem (1.b). From Theorem 1, we propose the design criteria of any one-to-one mapping coding schemes within one OFDM block (B = 1, so Kef f(X, ˆX) = K(1)ef f(X, ˆX) )

based on CP-reduced OFDM systems under symbol-wise Rayleigh fading channels.

Design Criteria 1: For virtual space-frequency codes within one OFDM symbol based on CP-reduced OFDM systems under symbol-wise Rayleigh fading channels, the design criteria are given as following.

I Rank (diversity) Criterion:

• For N ≥ (L + 1): Design a one-to-one mapping coding scheme, and then such a

code can always achieve full diversity of (L + 1).

• For N < (L + 1): Maximize the minimum rank of codeword distance matrix

A1(X, ˆX) over all pairs of distinct OFDM symbols.

I Determinant Criterion: Maximize th minimum determinant of total effective dis-tance matrix Kef f(X, ˆX) over all pairs of distinct OFDM symbols.

Unlike the diversity criterion of conventional SFCs, Design Criterion 1 raises a different diversity criterion in the case of N ≥ (L + 1). Since the codes designed to be one-to-one mapping are able to achieved full diversity for N ≥ (L + 1), the coding redundancy shall be used to enlarge the determinant of Kef f(X, ˆX), rather than the rank of Kef f(X, ˆX), which

means the diversity order in this setting is no longer determined by the minimum rank of the codes over all pairs of the distinct OFDM symbols, but determined by the channel order. On the other case of N < (L + 1), the rank of Kef f(X, ˆX) is upper bounded by N ×

rank(A1(X, ˆX)), thus maximize the rank of the codeword distance matrix is still be the main

concern of code design which is coincided with the diversity criterion of conventional SFCs. The determinant criterion is consistent in both circumstances, in order to minimize the error probability, the minimum determinant of Kef f(X, ˆX) should be maximized. For a code set

outperforms other codes of the code set, thus we define the effective codeword distance to be the minimum determinant of Kef f(X, ˆX) as a measure to evaluate of the superiority of

different coding schemes when they have equivalent achievable diversity. Based on Design Criterion 1, we propose the design critera of any one-to-one mapping virtual space-frequency codes for consecutive B OFDM blocks based on CP-reduced OFDM systems under symbol-wise Rayleigh fading channels.

Design Criteria 2: For virtual space-frequency codes for consecutive B OFDM blocks based on CP-reduced OFDM systems under symbol-wise Rayleigh fading channels, the design criteria are given as following.

I Rank (diversity) Criterion:

• For N ≥ (L + 1): Maximize the number of nonzero ith effective codeword

distance matrix K(i)_{ef f}(X, ˆX) for each block index over all pairs of distinct con-secutive B OFDM blocks.

• For N < (L + 1): Maximize the minimum rank of total effective distance matrix

Kef f(X, ˆX) over all pairs of distinct consecutive B OFDM symbols.

I Determinant Criterion: Maximize the minimum determinant of total effective dis-tance matrix Kef f(X, ˆX) over all pairs of distinct consecutive B OFDM symbols.

Because only if the codes have its K(i)_{ef f}(X, ˆX) 6= 0 for ∀X 6= ˆX, the codes achieve full diversity in ith block index. Therefore, we should maximize the number of nonzero effective codeword distance matrix for individual block index in the case of N ≥ (L+1), and then the maximum achievable diversity order of the codes is the multiplication of channel order and the number of nonzero ith effective codeword distance matrix out of B OFDM block indexes. For N > (L + 1), the diversity gain is maximized by enlarging the rank of Kef f(X, ˆX), to be

more exact, it is done by maximizing the rank of Ai(X, ˆX) for each block index. Moreover,

the determinant criterion claims that for the codes own larger effective codeword distance have the larger coding gain under the same diversity order, so the minimum determinant of Kef f(X, ˆX) should be maximized.

Chapter 5

Simulation Results

In addition to theoretical analysis, we also carry out simulations to investigate the perfor-mance of virtual space-frequency codes based on CP-reduced OFDM systems by choosing bit-error rate (BER) as our figure of merit, and the BER plots are also used to demonstrate the derived maximum diversity order and design criteria in Chapter 4. The global setting of the simulations and the assumptions are given as following.

Global setting and assumptions:

• Assume the CSI is available at the receiver side, and the ISI component can be

canceled perfectly. Timing and frequency synchronizations are assumed to be perfect as well.

• We employ QPSK modulation for all OFDM systems, and use the ML decoder to

detect signals.

• There are two types of Rayleigh fading channels used in simulations corresponding

to different delay spread, and their power profile are specified as following.

. For L = 1, the channel power profile is [ 0.8, 0.2 ].

. For L = 2, the channel power profile is [ 0.642, 0.256, 0.102 ] (SUI-4)[31]. A. Demonstrate the maximum achievable diversity order for N ≥ (L + 1)

From the derivation of achievable diversity bound in Chapter 4, we asserts that the maximum achievable diversity order of virtual space-frequency coding within one OFDM

symbol based on CP-reduced OFDM systems for N ≥ (L + 1) is upper bounded by channel order rather than the rank of effective codeword distance matrix, and this fact disagrees with the common sense of the rank criterion of conventional SFCs. Therefore we apply orthogonal designed SFBCs as the virtual space-frequency codes with their ranks are smaller or larger than the channel order to examine whether the slope of the BER curves is consistent with the channel order or the rank of the SFBCs. There are three orthogonal designed SFBCs applied in the simulations [32][33], and their codeword matrices are given by

SFBC4×2 =        x1 x2 −x∗ 2 x1 x∗ 3 √ 2 x∗ 3 √ 2 x∗ 3 √ 2 −x∗ 3 √ 2        , SFBC4×4=        x1 x2 √x3₂ √x3₂ −x∗ 2 x1 √x3₂ −x√₂3 x∗ 3 √ 2 x∗ 3 √ 2 −x1−x_√∗1+x2−x∗2 2 −x2−x_√∗2+x1−x∗1 2 x∗ 3 √ 2 −x∗ 3 √ 2 x2+x∗2_√+x1−x∗1 2 −x1−x_√∗1−x2+x∗2 2        , and SFBC8×8 =                   x1 x2 x3 0 x4 x5 x6 0 −x∗ 2 x∗1 0 x3 −x∗5 x∗4 0 x6 −x∗ 3 0 x∗1 −x2 −x∗6 0 x∗4 −x5 0 −x∗ 3 x∗2 x1 0 −x∗6 x∗5 x4 x4 x5 x6 0 x1 x2 x3 0 −x∗ 5 x∗4 0 x6 −x∗2 x∗1 0 x3 −x∗ 6 0 x∗4 −x5 −x∗3 0 x∗1 −x2 0 −x∗ 6 x∗5 x4 0 −x∗3 x∗2 x1                   , (5.1) where xi, i = 1, . . . , 6, are the constellation points of QPSK modulation. All SFBCs listed in

(5.1) can achieve full diversity, so the rank of SFBC4×2, SFBC4×4, and SFBC8×8are given

accordingly as 2, 4, and 8. And the SFBCs used here have one-to-one correspondence, thus applying the SFBCs to the CP-reduced OFDM systems when N ≥ (L + 1) shall achieve the full diversity of (L + 1). Moreover, note that the subcarriers are playing the role of virtual spatial domain, and we assume the channel is static during each SFBC transmission which is quasi-static fading.

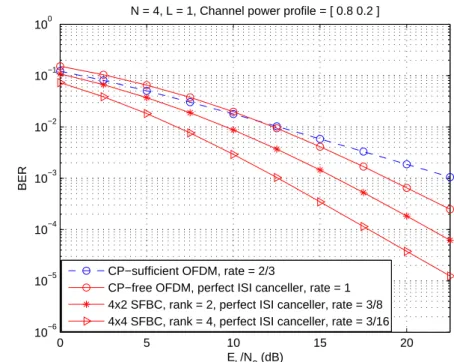
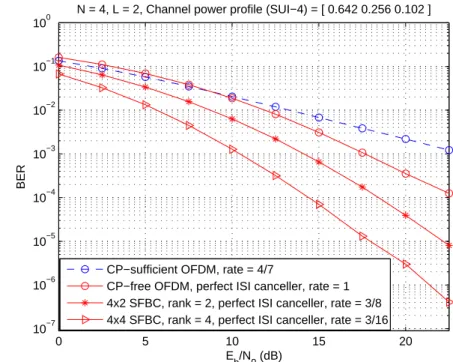
For N = 4 and L = 1, we intentionally apply the SFBCs with rank 2 and 4 based on CP-free OFDM systems with perfect ISI canceler to examine if the achievable diversity

order is channel order. As shown in Figure 5.1, the slope of BER curve corresponding to SFBC4×2 is consistent to the slope of SFBC4×4, and it is about the order of 2. As matter

of fact, we can classify the same fact by computing the minimum rank of K(1)_{ef f}(X, ˆX) for all distinct pair of OFDM symbols, and the minimum value of K(1)_{ef f}(X, ˆX) is truly 2 which coincides with the simulation results. Furthermore, the effective codeword distance of SFBC4×4 (the minimum det

³

K(1)_{ef f}(X, ˆX)´of SFBC4×4) is 0.1584 which is larger than

the effective codeword distance of SFBC4×2 (0.048), consequently, SFBC4×4 outperforms

SFBC4×2 as shown in Figure 5.1. And we note that the uncoded CP-free OFDM systems

have better performance than the CP-sufficient (which means the CP length is equal to the maximum delay spread) OFDM systems, only if the CP-free OFDM systems have the perfect ISI canceler and the receiver considers the ICI responses of all subcarriers to decode signals. The similar fact can be observed when the subcarrier number is enlarge to 8 in Figure 5.2, the SFBC applied here has an extremely large rank of 8, but the diversity order of SFBC coded CP-free OFDM systems still follows the channel order of 2.

As given in Figure 5.3, the achievable diversity order when N = 4 and L = 2 corre-sponding to SFBC4×2 and SFBC4×4 are both being the maximum delay spread instead

of the rank of SFBCs again. It may be hard to accept that SFBC4×2 coded CP-free

OFDM systems can achieve diversity order of 3. Once we analyze the upper bound of

rank

³

K(1)_{ef f}(X, ˆX) ´

, it may be believable. The rank of SFBC4×2 is 2, therefore the rank

of Ki(X, ˆX) is 2N; meanwhile, the rank of Rh is proved to be channel order. Recall (4.22),

as a result, the rank of effective codeword matrix is upper bounded by the channel order which matches the slope of the BER curve of SFBC4×2, and this fact also can be proved

by means of computing the minimum value of rank ³

K(1)_{ef f}(X, ˆX) ´

over all pairs of OFDM symbols. We enlarge the subcarrier number as 8 to simulate under the same multipath channel setting, and the BER plots in Figure 5.4 confirm that the achievable diversity is the maximum delay spread in this setup, too. At this point, we have verified the achievable diversity order of virtual space-frequency coding within one OFDM block based on CP-free OFDM systems by computer simulations, and also classified that if there are several