ERROR ANALYSIS OF QUATERNION TRANSFORMATIONS

I. INTRODUCTION

Error Analysis

Tra n

sf

o

r

m a

t

i

o

I

YEON FUH JlANG W PING LIN

National Chiao T h g University 'Eiiwan

In inertial navigation systems, the gyroscopes and accelerometers are often used to measure the angular velocity and specific force of the vehicle, respectively. While the inertial sensors are mounted directly to the vehicle in a strapdown system, the measured quantities are in body coordinates. In order to attain the navigation purposes, coordinate transformation matrix is needed to resolve the sensed specific force into the navigational reference frame for determining the velocity and position of the vehicle. Also,

the attitude information may be extracted from the transformed direction cosine matrix. The establishment of an accurate mathematical

of Quaternion

7s

T btransformation formulas are derived that related the

quateraions to the direction cosine matrix used in strapdown inertial systens 'banformation errors associated with these formulps are fully snslyzed. The drift errors evaluated under constant angular velocity have been shown to vary slightly among

three different transformatiom. It is shown that the skew errors in three transformation schemes a r e not all intrinsically zero. Yet the scale errors may differ largely by two orders of magnitude among

transformation schemes. This may become a selection criteria for selection of attitude tramformation schemes.

Manuscript received July 24,1990, revised October 9,1990.

transformation which is related to the gyro outputs is a vital computational problem in designing a strapdown inertial system.

Among the computational techniques for solving the transformation problem, two popular schemes are the direction cosine matrix and the quaternion [l, 2, 31. In most practical strapdown systems, the quaternions (Euler parameters) are updated periodically at a fast rate and then the direction cosine matrix which are composed of the quaternions are calculated at a slower rate. The main advantages of this approach are that it requires less computing time, gives better accuracy, and avoids the singularity problem. These are inherent properties associated with the quaternion dynamics, since it contains only four parameters and uses the half angular increments [5].

Generally, for all kinds of transformation, there are three transformation errors: the skew error, the scale error and the drift error [l-31. It is very important to investigate these errors before designing an adequate attitude algorithm to be built in the navigation computer. Early research workers [l-31 showed that the quaternion scheme is superior since it has less transformation errors than dirction cosine matrix. They claimed that the skew errors are inherently zero when the quaternion method is employed. We have found that this interesting property results from a particular transformation formula only. Since the transformation from quaternion to direction cosine matrix is not unique, hence the errors are varied in using different transformation formulas. The problem of selecting the best suitable form for strapdown inertial system applications gives us an impetus to reexamine the errors contained in different transformation formulas.

IEEE Log No. 91OO904.

Authors' addresses: Y. E Jiang, Institute of Electronics, National Chiao l h g Univemity, Hsinchu, 'Eiiwan, R.O.C.; y. p. Lin, Institute

of Control Engineering, National Chiao lbng University, Hsinchu, 'Eiiwan, R.O.C.

0018-%!51/91~00-0634 $1.00 @ 1991 IEEE

Three transformation formulas are derived here which can transform the quaternions into direction Cosines. h error model associated with the computed direction cosine matrix is briefly discussed. Error analysis is fully evaluated analytically and tabulated for comparison. Some useful conclusions can be drawn from the analysis and discussions.

11. THREE TRANSFORMATION FORMULAS

Let q = qo

+

qli

+

q 2 j

+

q 3 i be the rotation quaternion of the body axes with respect to the navigational reference axes, then any vector v that is transformed from body coordinates vb into navigational coordinates v" can be written as

v" = qvbq' (1) where q' is the conjugate of q. The equivalent transformation of using the direction cosine matrix C

where I is the identity matrix and

0 - 4 3 $2

[ + X I =

[

$3 0

-;j

4 2 $1

represents the equivalent vector cross-product operation associated with the rotation vector

4.

In terms of the components of

4,

the direction cosine matrix can be expressed as

sin$ l - c o s $ $1 $3 $2 $ $1$2 -$2+ $ (5)

Sin $ l - C O S $ 2 sin$ 1-cos$ sin$ l - c o s $ sin$ l - c o s $ l - C O S $ 2 ($1 + $:) - 7 @ 1 + 7 $ 2 $ 3 $1$2 I-- $ $2 $2$3 I-- $2 ($1 +

$3

$2 $1$3 -$I+ -- _{$ $ 2 + -}

is given by Using the quaternions definition:

9

qo = cos- 2 $i

.

$ q; = -sin-, $ 2 (6) v" = C V b . (2)

Using the quaternion algebra [l, 2, 51 in (1) and

i = 1,2,3 comparing with (2), yields the first transformation

formula:

and (1 - cos$ = 2sin2$/2) in

(9,

after simplifying

40" + 4: - 42" - 43" 2(qlq2 - 4043) q4143 + 4042) _{yields the second transformation formula:} 2(qlq2 4- 4043) q i - 4: + 422- 4: 2(4243 - 4041)

1

.

(3) This equation has been widely employed for the analysis and design of strapdown inertial systems A second set of transformation equations can be readily obtained by letting

4

= [$1,$2,$3IT be the rotation vector with magnitude (rotation angle) $ =

(0:

+

$;

+

$:)'I2, then the associated direction cosine matrix can be written as [6,

7]

[1-41*

[ 4 X l 2

(4) sin $ 1 - cos$

c

= I +

-[4x]

+

~ $ $2

44T*

(8) Sin $ 1 - cos$

c

= Icos$

+

-[4x]

+

- $ $2

In terms of the components of

4,

the direction cosine matrix can be rearranged as

1 -cos$ Sin $ $2 $1$2 -$2

4

+

- $2 cos$J $193

1

(9) l - C O S $ 2 $1$2 cos$+ ~ $2 --

G2

4

$2 sin$ l - c o s $ $1$3 - $ I + - $2$3 cos$+-

Obviously, these three transformation equations (3), (7), and (10) are equivalent if the quaternions satisfy the condition of normality, i.e.,

It is seen that transformation matrices C2 and C3 need equal computation time (ten multiplications, twelve additions and nine scaling shifts). Three more additions and three less scaling shifts are required for C1. Hence, C2 and C3 compute slightly faster than C1. I l l . ERROR M O D E L OF DIRECTION COSINE

MATRIX

Since the quaternions are transformed into a direction cosine matrix through various forms, the error analysis may be carried out for the corrsponding computed matrix. The skew, scale, and drift errors in a direction cosine matrix are now formulated for the convenience of error analysis.

Let B denote the true transformation matrix. By definition, B is orthogonal and also satisfy the orthonormal condition:

B ~ B =

z

(12) where BT is the transpose of B.

In

a practical

strapdown navigation system, assume the computed transformation matrix, C, is available, then C and B can be related by [3]

C = B ( I +

U

+S) ₍₁₃₎

where

U

and S represent the antisymmetric part and symmetric part of a small perturbed error matrix, respectively.

first-order approximation in S and

U ,

Using (12) and (13), it is easily found that, to the

cTc

= z + 2 s (14) which physically shows that the diagonal elements of S are the scale errors and that the offdiagonal elements of 2 s are the skew errors.

Equation (13) can also be written approximately as C = B(Z

+

U ) ( I

+

S).

BTC(Z

+

S)-' = I

+

U.

(15)

(16) Using (12) and taking matrix inverse in (15), yields

Therefore, if the skew and scale errors in C are corrected, then the offdiagonal elements of

U

represent the drift errors of C relative to B by physical interpretation. In order to compute the matrix

U

more accurately, transposing (16) and using

ST

= S and

UT =

-U,

yields

(Z

+

S)-'CTB = I

-

U.

₍₁₇₎ Subtracting (17) from (16) and using (12) and (13) and neglecting high-order approximations, it can be found that

U

= i(BTC- CTB). (18) It is obvious, from (14), that skew and scale errors may be computed from matrix C alone; while from (18), evaluation of drift errors must rest upon B and C.

IV. ERROR ANALYSIS: SKEW A N D SCALE ERRORS

The skew and scale errors can be found by applying (14) to (3), (7), and (lo), respectively. The results are shown as follows: for matrix C1, we have

CTC1 =

z

+

2s1 = (402 + q: + q; + q 3 2 z =

z +

[(q;

+

q;

+

q;

+

q;)2 - 111 (19) (20) c1i = 0, i = 1,2,3 (21) which shows that the skew error for i-axis of C1 is

and the scale error for i-axis of C, is

61i = i[(q:

+

q;

+

q;

+

q32)2 -

11,

i = 1,2,3. (22) Similarly, for matrix C2, we have

CTC? =

z

+

2s2 =

z

+

4(qi

+

q:

+

q;

+

q; - 1)

1

q22+q32 -q1q2 -qlq3 -41q2 d + q : -q2q3

[

-41 43 -4243 q ; + d which shows that the skew error for i-axis of C, is

c2i = -4(q0"

+

4:

+

q;

+

q: - 1)qjqk i = 1,2,3

{

k = 3,1,2

j = 2,3,1

.

(24)

Note that

i,

j , and k are in permutative order. And the

scale error for i-axis of C2 is

62i = 2(qo'

+

412

+

422

+

q32 -

+

q 3 i = 1,2,3

j = 2,3,1

.

(25) k = 3,1,2

TABLE I Quaternion Approximations

order transformation matrix form

1

order

1

quaternions

which shows that the.skew error for i-axis of C3 is

~ 3 i = 4(q$

+

4:

+

qi

+

4: - 1)qjqk i = 1,2,3

i

k = 3,1,2

j = 2,3,1 (27)

and the scale error for i-axis of C3 is

63 = 2(q$

+

q;

+

qg

+

q: - 1)(&

+

qf), i = 1,2,3.

(28) Thus, it is observed from (20), (23), and (26) that all the skew and scale errors are zero for C,, C, and C3 if the quaternions satisfy the condition of normality (11). ?he skew errors associated with matrix C1 are inherently zero, but it is not true all the time for C2 and C3. In addition, the skew errors in

C2

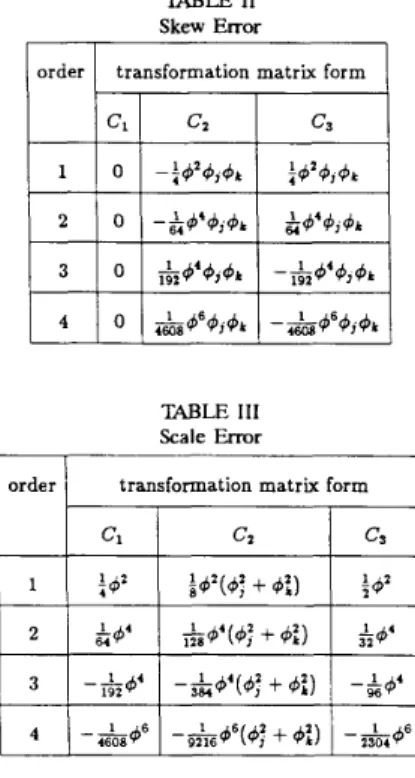
and C3 are zero if the body rotation is along one of the principal axis. The scale errors are all equal in three axes of C1, but they are not equal in three axes of C2 and C3. The skew error in C2 and C3 associated with the same direction has equal magnitude but in the opposite direction.

quaternions are approximated by truncating the transcendental functions in (6). Bble I gives the approxinfated quaternions for first order through fourth order [l]. Substituting the values of the approximated quaternions into (22), (24), (25), (27), and (28) the low-order approximation of skew and scale error for i-axis of C1, C2, and C3 are listed in a b l e I1 and B b l e 111, respectively.

Obviously, as comparing with C1, the scale errors are twice larger and the skew errors are increasing a In a practical strapdown navigator, the computed

TABLE I11 Scale Error

little in C3. However, the large decrease by two orders of magnitude in scale errors in C2 is achieved at the expense of a slight increase in skew errors. This effect may offer a longer renormalization period in correcting the orthgonality. In this respect, it is suitable for short range inertial guidance systems such as short range tactical missles.

V. ERROR ANALYSIS: DRIFT ERRORS

In order to analyze the drift errors in a computed direction cosine matrix, the true transformation matrix B is required. Assuming that the direction of the angular velocity vector w = [w1,w2,w31T is constant over the integration interval ( t , t

+

AT), then the true matrix B is given as the right-hand side of (5) or (9) with

$; = [ + A T w i d t , t i = 1,2,3 (29) where AT represents the sampling period. The drift errors may be found by applying (18) to (3), (7) and (lo), respectively. The results are as follows:

Uj = $(BTCj - CTB)

o

-ej3

ej2

-

-

JIANG & LIN: ERROR ANALYSIS O F QUATERNION TRANSFORMATIONS

~ ~ ~~~

TABLE IV Drill Error

I

order

I

t;nsfoynati; m a t 7 ;of

1

For matrix C1,

represents the drift error about i-axis of matrix C1. By neglecting high order terms, it can be written as

For matrix C2, we have

i = 1,2,3 (33) and similarly, for matrix C3, we have

i = 1,2,3. (34) It is evident that the drift errors in these three matrices are all equal if the condition of normality (11) is satisfied. Substituting the values of the approximated quaternions given in 'hble I into (32)-(34), the low order approximation of drift errors for i-axis of C1, C2,

and C3 are listed in 'Itrble IV. Note that the drift errors in C2 and C3 are only slightly different from that in C1.

The transformation errors in matrix C1 have been presented by Wilcox [l] and Mckern [2]; we list them

in the tables for the convenience of comparison and completeness.

VI. CONCLUSIONS

We provide the derivation of three often

encountered transformation formulas which transform quaternions into direction cosine matrix. Their analytic transformation errors are evaluated and tabulated for comparison.

It has been shown that the skew errors in these transformation matrices are not all zero. It is zero only for transformation matrix C1. The scale errors are not equally distributed except for C1. They are

axis dependent. The transformation matrix Cz has the smallest scale error which may enable the extension of the renormalization period. The drift errors are only slightly different in these three transformation matrices.

These results are helpful in the design of attitude algorithms for strapdown inertial navigation systems. REFERENCES

(31)

(11 Wilcax, J. C. (1967)

A new algorithm for strappeddown inertial navigation.

IEEE Transactions on Aerospace and Electronic Systems, AES-3, 5 (Sept. 1%7), 79&8U2.

A study of transformation algorithms for use in a digital computer.

Masters thesis, T493, Massachusetts Institute of Technology, Cambridge, 1968.

Strapdown guidance e m r analysis.

IEEE Transactions on Aerarpace and Electronic Systems, [2] Mckern, R. A. (1968)

[3] Mortensen, R. E. (1974)

A E S - L O , 4 (July 1974), 451457. [4] Friedland, B. (1978)

Analysis strapdown navigation using quaternions

IEEE Transactions on Aerarpace and Electronic Systemr,

AES-14, 5 (Sept. 1978), 764-768. Morse, P. M., and Feshbach, H. (1973)

Methoak of Theoretical Physics.

New York McGraw-Hill, 1973, 73-76.

A new mathematical formulation for strapdown inertial navigation.

IEEE Transactions on Aerospace and Electronic Systems, AES-7, 1 (Jan. 1971), 61-66.

Classical Mechanics (2nd ed.).

Reading, MA: Addison-Wsley, 1980,158-16.

[5]

[6] Bortz, J. E. (1971)

[7] Goldstein, H. (1980)

Yeon Fuh Jiang was born in 'hiwan, R.O.C., on April 10, 1954. He received the B.S. and the M.S. degree in physics from the University of Chinese Culture and the National Tsing Hua University in 1976 and 1978, respectively. He is currently a doctoral student in the Institute of Electronics, National Chiao Tung University, R.O.C.

After serving for two years in the Chinese Army, he was employed by the Chung Shan Institute of Science and Technology from 1980 to 1987. His areas of interest are the design and analysis of inertial navigation systems and inertial technology and control engineering.

Mr. Jiang is a student member of the IEEE, and a member of Phi B u Phi.

Yu Ping Lin was born in Kwangsi, China, on Dec. 10, 1929. He received the

B.S.

degree in mechanical engineering from the Chinese Naval College of

Technology in 1953, the B.S. in electrical engineering from the United States Naval Postgraduate School in 1965, and the M.S. degree in electrical engineering from Stanford University, Stanford, CA, in 1972.

faculty member of Chung Cheng College of Science and Technology as Professor of System Engineering for ten years. He is currently the Professor and Chairman of the Control Engineering Department, National Chiao Tung University, Hsinchu, Biwan, R.O.C.

Mr. Lin was a fellow of the Center for Advanced Engineering Studies, M.I.T. in 1975-1976, specializing in inertial navigation.

He served in the Chinese Navy as a technical officer for eight years, and was a

JIANG & LIN ERROR ANALYSIS OF QUATERNION TRANSFORMATIONS

~ -~

~~