An approximate maximum entropy solution for bearing estimation of coherent sources

U4.11

AN APPROXIMATE MAXIMUM ENTROPY SOLUTION

FOR

BEARING ESTIMATION

OF

COHERENT SOURCES Jenho Tsao

Department of Electrical Engineering National Taiwan University

Taipei, Taiwan,

ROC.

ABSTRACT

This paper presents a new method to find an approximate solution of the maximum entropy (ME) method for bearing estimation. It is especially suitable for the coherent source problem. This solution clearly shows that the ME spectrum is an all-pole spectrum and the coefficients of its denominator polynomial can be found from the estimation error of signals. Since no spatial smoothing is required, it always provides a spectrum with whole array aperture, therefore it is possible to find a solution for two closely spaced sources with a S-element array, based on single snap-shot data. Depending on how signal is estimated, it is possible to find a superresolution spectrum with DFT only.

INTRODUCTION

Maximum entropy method (MEM) was introduced by Burg for superresolution spectrum analysis. Developements of its theory were well documented in [l]. Although MEM is related to the linear prediction theory closely, it is a non-linear optimization problem in general. Its solution can be found by the technique of Lagrange multiplier[2,3,4]. Algorithms to impliment the MEM can be found in [3]. In this paper, an approximate solution of the MEM was found. This solution clearly shows that the ME spectrum is an all-pole spectrum. Although how t o implement this solution optimumly is not known yet, simulation results dose show that it may

find a solution for two closely s p x e d sources with a %element array. It may provide spectrums with resolution higher than the well known MUSIC algorithm

[5],

since this solution can be found by using single snap-shot of data without spatial smoothing; that is, a larger order can be used in this solution.

Bearing estimation of coherent sources has a problem of inverting a singular covariance matrix[6]. To solve this problem, spatial smoothing must be applied. h d u c t i o n of aperture size is unavoidable in using spatial smoothing. Theoretically speaking, this is exact the problem of spectrum estimation of sinusodial processes based on a single set of measurement data. By linear prediction theory, to find a reliable AR spectrum of the sinusoidal process[7,8], the order of linear prediction filter must be less than the data length. In this paper the problem of bearing estimation of coherent sources is treated exactly same as the spectral estimation of sinusdial processes based on single snap-shot of data, since multiple snap-shot of data do not change the nature of this problem.

APPROXIMATE MAXIMUM ENTROPY SOLUTION

Since MEM is formulated on time domain conventionally, the usual time domain notations are used here for convinence. Following the standard notations in spectrum estimation and stationarity assumption, the power spectrum of a signal with autocorkelation sequence (ACS) r(n) is

This work was support by the National Science Council,

Rep. of China, under Contract NSC 774404-EoO2-07. P(f) =

Nyl

_N=O r(n) e-j2dnT ; n = O..N-1 (1)

2875

From the ME theory. P(f) is to be found by maximizing

H

=

I

In P(f) df and constrained by

r( n) = P( f) ej2nfnT df

I

; n = O..N-1 ( 2 ) By Lagrange multiplier technique, this object function can be formulated t o be an unconstrained one[9] as

N-1

In P(f) df

-

I.(.)

-

An

X

I

P(f) ej21fnTdf12 n =O

(3) where

A n

are the Lagrange mutipliers. Consider the discrete version of this objective function

where Pm= p(fm), wm=2dm = 2m8. Note that the Lagrange multipliers are set t o be a single variable A, this essentially makes the estimation error of r(n) be equally weighted. To find the solution of Pm, a set of non-linear equations must be solved, which are

T = 7 r . - 2 A

dJ

6f

= o

; i = 1..M

(5)

The IDFT of Pm is an estimate of r(n) which can be defined as

Equation

(5)

can be rewritten as

= o

;i = 1..M _{( 7)}

2876

Equation (5) is a complicated equation of Pi

,

since P.

exist inside the bracket of (5) when m = i. However, P.

exist on the left-hand side of (7) only, a solution of (7)

can be found to be 6f P. =

; i = 1..M (8)

This is an approximate solution of the ME spectrum, since Pi are not exactly solved from (4), and the spectrum found is named approximate maximum entropy(AME) spectrum here. Equation (8) tells us that Pi is proportional to the inverse of the discrete Fourier transform( DFT) of the estimation error sequence

a(n) = r(n)

-

;(n) ; n = O..N-1; (9) This result does not provide a n y direct solution of Pi, however, it provides a general way to find Pi; that is, an estimate of the ACS, i(n), in stead of the interested spectrum must be found first; then the estimation error of the ACS can be used to find the spectrum indirectly. Since the assumed known data is the ACS r(n), i ( n ) must be estimate from r(n). This is a problem similiar to the signal reconstruction problem. One point worth to mention is that ;(n) is an estimate of the true ACS in stead of the given measured data r(n). There are many techniques to do signal reconstruction. One simple method to find

i(n)

is given in next section. From the theory of MUSIC algorithm, this result has a common requirement of finding an estimate of the "noise" vecter d n ) , although the AME solution does not provide a clear way to find it.

ESTIMATE O F i(n)

An easy way to estimate ;(n) from r(n) is by defining

N-1

- X

r(n) e-jUmnT ; m = l..M, and qm

-

N=O

where I is a set of k's, for which Iqk

I

>

,d

and ,d is a threshold t o discriminate the noise background in qm from signal responses. The intermediate spectrum of qm is a low resolution one, since N is a small number in general. It is well known that from the DFT and IDFT pair of (lo), r ( n ) might be exactly equal to r(n), if the discrimination threshold is not applied. In theory, the value of ,d can be set by a priori knowledge about the noise level or by the sidelobe level of signals in qm.

To get a minimum error estimate of i(n) from

i(n)

,

the distance between

i(n)

and r(n) is minimized by a scaling factor y as

N-1

m i n

z

l r ( n ) - y i ( n ) 1 2 y n=O

Then ;(n) = y

i(n)

is used as the desired estimate of true ACS. This minimization can be done easily and it essentially reduces the sensitivity of what value of ,b is used in (10).

Note that the algorithm given above to estimate ;(n) is not a general one, since it is not an estimator found in any optimum sense; however, from previous simulation results, this algorithm is good enough for cases similiar t o the examples given in next section. Because the AME solution does not put any clear condition on q n ) , orther resonable methods t o find ?(n) might yield an equally good AME solution also. In

general, the optimum method to find i(n) is not known. SIMULATIONS

T o show performances of the AME solution, two simulation examples of coherent source bearing estimation are given here. They represent the cases that are solvable and unsolvable with conventional bearing estimation techniques. Since time domain formulation

as used in previous sections, some simple conversions of time to spatial domain variables are necessary, the major one is the spatial frequency variable U = sin 0,

where 8 is the angle measured from array broadside. The first example has two sources with bearings ut = 0.0, u2 =

0.25

and their associated phases

41

= 0.0,

Cpz

= 30 degrees. Each source has a SNR of

20 dB.

The receiving array has

6

elements which are spaced at half wavelength. This is a solvable case by applying spatial smoothing and the well known MUSIC algorithm. Results of applying these techniques are given in Fig. 1

with an order of

4.

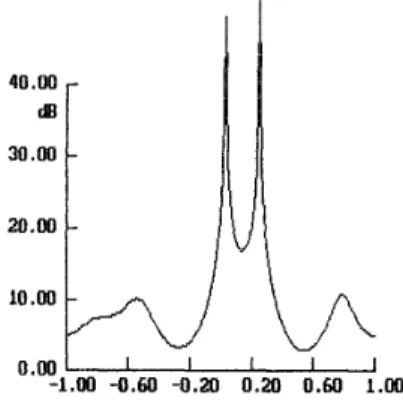
Results of ten test runs, based on single snap-shot data, are overlaied together. It can be found that there are many spurious peaks due to excessive order used. Therefore, the same data were processed again with an order of 3 and the results are shown in Fig 2. It can be found that the two sources are resolved in most cases. The same set of data were processed by the AME technique, its results are given in Fig. 3. It can be found that spurious peaks exist due to a large order of 6 being used also. To cure this problem, the coefficients a(n) estimated from ten snap-shot data were averaged to be a new estimate of a(n), the result is given in Fig.

4.

It can be found that this result is much better than the previous results, since very sharp peaks were pointed to the target directions correctly.

The second example has a similiar scenario as the first example. The target bearings are U I = 0.2, u2= - 2 5 and their associated phases are

41

= 0.0,

&

= 30

degrees. The receiving array has 3 elements only. This is a unsolvable case by applying conventional techniques. Results of the AME solution are given in Fig. 5, in which the curves with lower resolution are results of simple DFT angular spectrum. It can be found that both targets are resolved well based on single snap-shot data only.

RFERENCES

[l] D.

G.

Childers ed., Modern Spectrum Analysis,

[2]

J.

P. Burg "Maximum Entropy Spectral Analysis,"

[3] T.

J.

Ulrych and T. N. Bishop, "Maximum Entropy IEEE Press, 1978.

PhD. dissertation, Stanford Univ., May, 1975.

Spectrd Analysis and Autoregressive Decomposition,"

Rev. Geophys. Space Phys., Vo1.13 Feb. 1975.

[4]

J.

A. Edward and M.

M.

Fitelson, "Notes on Maximum-Entrow Processing." IEEE Tran. Inform. Y l

Theory, IT-19, 1973.

[5]

R.

0.

Schmidt "A Signal Subspace Approxh to Multiple Emitter Location and Spectral Estimation,'' PhD. dissertation, Stanford Univ., 1981.

[S] T.

J.

Shan, M. Wax and T. Kailath "On Spatial smoothing for Direction-of-Arrival Estimation of Coherent"Signals," IEEE trans. ASSP-33, Auq 1985. [7] W.F. Garbriel, "Spectral Analysis and Adaptive

Array Superresolution Techniques", IEEE proc. June 1980.

(81 S.M. Kay, S.L. Marpie, "Spectrum Analysis

-

A Modern Perspective", IEEE Proc. Nov. 1981. [9] S.

J.

Wernecke and L. R. D'A$lario, "Maximum

Entropy Ima e Reconstruction, IEEE Trans. on Computers, f p r l 1977. 40 .00 du 30 .a0 20.00 10 .00 0 .00 -1.00 6.60 -0.20 0.20 0.60 1 . .00 U

Figure 1. The MUSIC an lar spectrum of two target with a 6-element array. TB", targets have e ual SNR of 20 dB and their (bearing, phase) are (0.0, 0.3 and (0.25,

30").

Spatial smoothin is applied to get an o r d e r 4 covariance matrix. Resufts of ten test runs are overlaid.

: i ~

10 0.00 .00

-1.00

_I

1

.m

U

Fi ure 2. Same conditions as in Figure 1, except the orjer used is 3. I 40.00 r dB 30.M 20 .00 10 .00 0.00 -1.00 6.60 -0.20 0.20 0.60 1.00 U

Figure

3.

The AME spectrum of the s a n e signals used in Figure 1. 40.00 CfB 30.00 z0.M 10.00 0.00 -1.00 -0.60 -0.20 0.20 0.60 1.00 U

Figure

4.

The averaged AME solution from results of 10

snapshot data given in Figure 3.

1 1 40.00

I

IP -1.Dfr -0.60 -0.20 0.20 0.60 1.OD U

Figure 5. The AME spectrum of two targets with a 3-element array. The targets have equal SNR of 20 dJ3 and their (bearing, phase) are (0.2, 0') and

(-.25,

30"). The lower resolution curves are the DFT spectrum.