Two Variations of the Minimum Steiner Problem
§
Tsan-sheng Hsu
†, Kuo-Hui Tsai
∗‡, Da-Wei Wang
†‡¶and D. T. Lee
†?August 12, 2003
Abstract
Given a set S of starting vertices and a set T of terminating vertices in a graph G = (V, E) with non-negative weights on edges, the minimum Steiner network problem is to find a subgraph of G with the minimum total edge weight. In such a subgraph, we require that for each vertex s∈ S and t ∈ T , there is a path from s to a terminating vertex as well as a path from a starting vertex to t. This problem can easily be proven NP-hard. For solving the minimum Steiner network problem, we first present an algorithm that runs in time and space that both are polynomial in n with constant degrees, but exponential in |S| + |T |, where n is the number of vertices in G. Then we present an algorithm that uses space that is quadratic in n and runs in time that is polynomial in n with a degree O(max{max{|S|, |T |} − 2, min{|S|, |T |} − 1}). In spite of this degree, we prove that the number of Steiner vertices in our solution can be as large as|S| + |T | − 2. Our algorithm can enumerate all possible optimal solutions. The input graph G can either be undirected or directed acyclic. We also give a linear time algorithm for the special case when min{|S|, |T |} = 1 and max{|S|, |T |} = 2.
The minimum union paths problem is similar to the minimum Steiner network problem except that we are given a set H of hitting vertices in G in addition to the sets of starting and terminating vertices. We want to find a subgraph of G with the minimum total edge weight such that the conditions required by the minimum Steiner network problem are satisfied as well as the condition that every hitting vertex is on a path from a starting vertex to a terminating vertex. Furthermore, G must be directed acyclic. For solving the minimum union paths problem, we also present algorithms that have a time and space tradeoff similar to algorithms for the minimum Steiner network problem. We also give a linear time algorithm for the special case when|S| = 1, |T | = 1 and |H| = 2.
§An extended abstract of part of this paper appears in [7].
†Institute of Information Science, Academia Sinica, Nankang 11529, Taipei, Taiwan, ROC. E-mail:
{tshsu, wdw, dtlee}@iis.sinica.edu.tw.
‡Supported in part by the National Science Council, Taiwan, ROC, under Grant No.
NSC-83-0408-E-001-021.
∗Department of Computer Science, National Taiwan Ocean University, Taiwan, ROC. Email:
tsaikh@mail.ntou.edu.tw.
¶Corresponding author.
? Supported in part by the National Science Foundation under Grants CCR-9309743 and INT-9207212,
1
Introduction
Given a graph G = (V, E), a non-negative cost on each edge in E, and a set of vertices Z ⊂ V , the minimum Steiner problem is to find a minimum cost subgraph with a given property which spans Z. The vertices besides Z in the subgraph are Steiner vertices. For example, the minimum Steiner tree problem is one in which the subgraph is a tree. The minimum Steiner problem has many important applications and has been extensively studied [2, 8, 9, 15, 16]. In one of the latest survey papers [8], more than 300 references are listed.
Let S and T be two subsets of vertices of V . A subgraph G0 of G is said to be S, T -connected if for each vertex s ∈ S there exists a path1 in G0 from s to a vertex t ∈ T , and
for each vertex t ∈ T there exists a path in G0 from a vertex s ∈ S to t. We consider the following two variations of the minimum Steiner problem on graph G = (V, E) with a non-negative weight on each edge. The minimum Steiner network (MSN) problem is defined as follows. Given a set of starting vertices S and a set of terminating vertices T , we want to find a subgraph G∗ with the minimum total edge weight such that G∗ is S, T -connected if such a G∗ exists. The minimum union paths (MUP) problem is a generalized version of the minimum Steiner network problem. An additional set of hitting vertices H ⊂ V is specified, and the subgraph G∗, if exists, is required to contain H, and each vertex in H must be in a path from a starting vertex to a terminating vertex. Note that the minimum Steiner network problem is a special case of the minimum union paths problem in which the hitting set H is empty. It can be seen that the above two minimum Steiner problems are NP-hard by a polynomial transformation from the exact cover by the 3-sets problem (for an example, see the discussion in Chapter 1 of [9]).
Several important applications for solving the minimum Steiner problem on a directed acyclic graph are mentioned in [12] for finding a minimum Steiner arborescence. The two problems defined here can be used to solve generalized versions of these problems. For example, finding a minimum Steiner network can be used to design an optimal drainage system for a building where starting vertices are places to dump wastes and terminating vertices are sewers. Finding minimum union paths can be used to design an optimal system layout for an irrigation and drainage system where starting vertices are water sources, hitting vertices are places that need water, and terminating vertices are drains.
There are several types of algorithms that can be used to find an exact solution of the minimum Steiner problem which include dynamic programming [3], 0-1 linear programming [1], and exhaustive enumeration [10]. Though most of the discussions are on undirected
1In this paper, we refer to a path as a sequence of vertices a
1, a2, . . . , ak such that (ai, ai+1), 1≤ i < k,
graphs, they can be easily extended to directed graphs.
The time complexity of well-known approaches for solving the Steiner-tree-like problem is (1) exponential in the number of terminal vertices by a dynamic programming approach [3], or (2) polynomial in the number of vertices in the input graph with a degree equaling the number of Steiner vertices in a general graph by enumerating all possible candidates of Steiner vertices [10]. The dynamic programming approach uses more space than the enumerating approach. In this paper, we first develop a dynamic programming approach to solve our problems, then we develop our efficient enumerating algorithm.
A typical exhaustive enumeration algorithm for the minimum Steiner tree problem makes use of the fact that a minimum Steiner tree is a minimum spanning tree on the set of vertices in the solution. Thus, by properly choosing the set of Steiner vertices, we can easily find the solution by computing a minimum spanning tree. Therefore, finding an accurate upper bound on the number of Steiner vertices is crucial in estimating the running time of this type of algorithm. Let k be the above upper bound. The time complexity of the algorithm is O(nk·MST (G)), where MST (G) denotes the time complexity of finding a minimum spanning
tree of G. A similar algorithm can be devised to solve the MSN problem and the MUP problem in time exponential in k. We shall show that by exploiting some properties of the solutions to the two problems, we can solve them in time exponential roughly in k2.
Some related work for variations of the minimum Steiner problem on directed graphs can be found in [6, 11, 12, 13, 17]. In particular, Nastansky et al. [12] presented an efficient heuristic algorithm for solving the minimum Steiner arborescence problem on a directed acyclic graph by exhaustive enumeration. However, they do not provide any theoretical analysis on the time complexity of their algorithm, which we believe is exponential in k. Rao et al. [13] described an approximation algorithm for finding a minimum Steiner arborescence in a rectilinear plane rooted at the origin with the additional constraint that all paths from the root to the leaves must be the shortest.
In this paper, let n and m be the number of vertices and edges in G, respectively. In the MSN problem, let α = max{|S|, |T |}, let β = min{|S|, |T |} and let σ = |S| + |T |. In the MUPproblem, let γ = |S| + |H| + |T |.
Results in our paper are summarized in Table 1.
2
Minimum Steiner Network
For ease of description, we assume the graph G is directed acyclic. However, all of our discussions also hold for the case when G is undirected. We also omit the word “directed” when it does not cause confusion, and minimality of a solution network is assumed everywhere
Polynomial-time algorithms Quadratic-space algorithms Special case α = 2, β = 1 MSN time O(nm + n·3σ+ n2·2σ) O(nm + 2σ·α3·nmax{α−2,β−1}) O(n + m)
space O(n3·2σ) O(n2) O(n + m)
|S| = |T | = 1, |H| = 2 MUP time O(nm + γ!·n·((18γ)γ+ n·(8γ)γ)) O(nm + γ!·(8γ)γ·γ3·nγ−1) O(n + m)
space O(n3·4γ) O(n2) O(n + m)
Table 1: Summary of results. in the discussion.
Given two non-empty disjoint subsets of vertices S and T in G, a Steiner network of G is a subgraph G∗ of G such that G∗ is S, T -connected. The vertices in S are called starting vertices and those in T are terminating vertices. Any path in a Steiner network starting from a vertex in S and ending in a vertex in T is called an S-T path. If the edges in G are associated with non-negative weights, then a Steiner network with a minimum total edge weight is called a minimum Steiner network2 and denoted as MSN(G, S, T ). Note that in
a minimum Steiner network except for the two extreme vertices an S-T path may contain vertices in S or T .
2.1
Preliminaries
Before we describe our algorithm for finding a minimum Steiner network, we examine its properties. Through these properties, we give a structural description of a minimum Steiner network. Then we construct a minimum Steiner network by first efficiently enumerating all networks satisfying the above description and then picking one with the minimum cost.
Let S ˙∪T ˙∪Z be the set of vertices in MSN(G, S, T ), where ˙∪ is the disjoint set union operator. The vertices in Z, which contain no vertices in S and T , are Steiner vertices. We define the distance network for G, denoted D(G), to be the graph with the same set of vertices as G and there is an edge (u, v) in D(G) if and only if there is a path between u and v. The edge (u, v) is given a weight equal to the total weight of a shortest path from u to v in G.
Lemma 2.1 Given S and T , the cost of MSN(G, S, T ) is equal to the cost of
MSN(D(G), S, T ). Furthermore, given MSN(D(G), S, T ), MSN(G, S, T ) can be constructed in O(n + m) time.
2Here we consider the Steiner network with the least number of edges among those with a minimum total
Proof: Let P (u, v) denote a maximal path in MSN(G, S, T ) connecting vertices u and v for some u, v ∈ V such that the intermediate nodes in the path have in-degrees and out-degrees equal to 1. This lemma simply states that if we replace every such path P (u, v) in MSN(G, S, T ) with an edge (u, v) whose weight is equal to the total edge weight of all the edges in P (u, v), then the resulting network has a cost equal to MSN(D(G), S, T ). Note that the set of Steiner vertices Z in MSN(G, S, T ) can be partitioned into two sets Z = Z1∪Z˙ 2,
where Z2 contains the intermediate vertices of all such P (u, v) defined above and Z1 will be
the set of Steiner vertices in MSN(D(G), S, T ). 2
From Lemma 2.1, we know that it suffices to compute a minimum Steiner network from the distance network of the graph. We will focus our discussion on finding a minimum Steiner network in a distance network in order to show that in an acyclic graph, the possible candidates for Steiner vertices can be enumerated efficiently.
A Steiner vertex in MSN(D(G), S, T ) is convergent if its in-degree is greater than 1, and is divergent if its out-degree is greater than 1. From Lemma 2.1, any Steiner vertex in a minimum Steiner network of a distance network must be either convergent or divergent. Note that a vertex may be both convergent and divergent if its in-degree and out-degree are both greater than 1.
Lemma 2.2 Given a directed acyclic graph G with non-negative edge weights and two dis-joint subsets of vertices S and T , let s ∈ S, t ∈ T , and P be a path from s to t in MSN(D(G), S, T ) whose length (number of edges) is greater than 1. Let P = [s, w1, w2, . . . ,
wq, t], q ≥ 1. Then there exists b, 0 ≤ b ≤ q, such that exactly one of the following two
conditions is true: (1) wi, 1 ≤ i ≤ b, is convergent and wi, b ≤ i ≤ q, is divergent; (2)
wi, 1≤ i ≤ b, is convergent and wi, b + 1≤ i ≤ q, is divergent.
Proof: We prove this lemma by contradiction. Recall that MSN(D(G), S, T ) has a minimal number of edges. Let b be the largest index such that w1, . . . , wb−1, and wb are convergent in
P . Assume that wb+16= t is strictly divergent, i.e., not convergent, and that wais convergent,
where a > b + 1. Let H be the resulting graph obtained by removing the edge from wa−1 to wa from P , and hence from MSN(D(G), S, T ). Note that H remains a Steiner network
since wa is convergent and has another incoming edge. Since the weight of each edge is
non-negative, either the cost of H is less than that of MSN(D(G), S, T ) or H has a smaller number of edges. Thus MSN(D(G), S, T ) is not optimal, which is a contradiction. 2 The vertex wb in the path P as specified in Lemma 2.2 is referred to as a neutral vertex.
Note that if a vertex is neutral in an S-T path, then it is neutral in any other S-T path. Corollary 2.3 There exists at most one neutral vertex in the path P as specified in
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 1 2 3 12 15 5 23 24 10 11 29 4 22 6 7 8 9 13 14 16 17 20 21 15’ 18 19 25 26 27 28 16’
N
N
N
uNeutral Split Network
in out
Minimum Directed Steiner Network
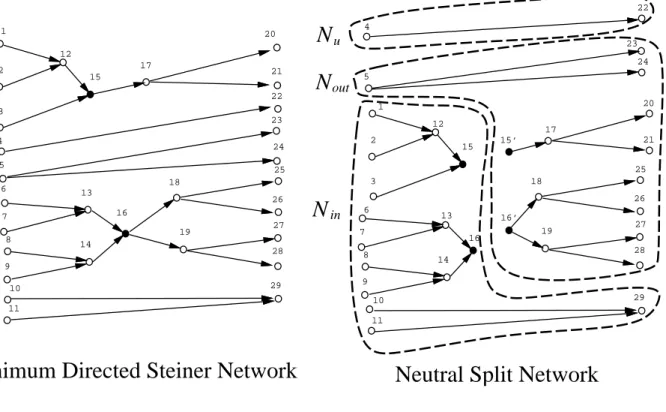
Figure 1: A minimum Steiner network, the set of neutral vertices shown in solid circles, and its neutral split network.
A directed graph is an incoming arborescence if either it is an isolated vertex or there exists exactly one root vertex u such that there is exactly one path from any other vertex to u. A collection of incoming arborescences is an incoming forest. A directed graph is an outgoing arborescence if it is an isolated vertex or there exists exactly one root vertex u such that there is exactly one path from u to any other vertex in the graph. A collection of outgoing arborescences is an outgoing forest. A vertex is a leaf in an incoming (respectively, outgoing) forest if its in-degree (respectively, out-degree) is zero. A vertex in a forest that is not a leaf is an internal vertex . Given a vertex u in a minimum Steiner network a split graph at u is the graph obtained by replacing u with two vertices u1 and u2, such that u1 inherits
all incoming edges of u, and u2 inherits all outgoing edges of u. Given MSN(D(G), S, T ), let
its neutral split network be defined by applying the split operation on every neutral vertex in MSN(D(G), S, T ). The cost of the neutral split network is the same as the cost of the original minimum Steiner network. Figure 1 illustrates a minimum Steiner network and its neutral split network. The set of neutral vertices are shown in solid circles, while the others are shown in hollow circles.
Lemma 2.4 There are at most σ− 2 Steiner vertices in MSN(D(G), S, T ), and the bound is tight.
Proof: We prove this lemma by induction on the value of σ. This lemma is obviously true when |S| = 1 and |T | = 1. For the induction step, observe that adding a vertex to S or T creates at most one Steiner vertex in D(G), by converting a vertex from MSN(G, S, T ) in Z2 into one which is in Z1. To prove that the bound is tight, let us construct, as described
below, a graph G such that MSN(D(G), S, T ) has exactly σ−2 Steiner vertices. Let BS be an
incoming arborescence with all equal weight edges such that the root is u, the set of leaves is S and the in-degree of each node except for the leaves (each of whose in-degree is 0) is 2 and its out-degree is 1 except for the root (whose out-degree is 0). For convenience BS is called an
incoming binary tree. Let BT be similarly defined except that it is an outgoing arborescence
(binary tree) whose root is v, and the set of leaves is T . Then G = BS∪ BT ∪ {(u, v)} is a
graph whose MSN(D(G), S, T ) contains σ− 2 Steiner vertices. 2
Lemma 2.5 The neutral split network of a minimum Steiner network MSN(D(G), S, T ) for an acyclic graph G with non-negative edge weights can be partitioned into three disjoint subgraphs Nu, Nin and Nout where (1) Nu consists of edges from a vertex in S to a vertex
in T ; (2) Nin is an incoming forest where each leaf is a vertex in S, each non-root internal
vertex is a Steiner vertex, and each root is either a Steiner vertex or a vertex in T ; (3) Nout is an outgoing forest where each leaf is a vertex in T , each non-root internal vertex is
a Steiner vertex, and each root is either a Steiner vertex or a vertex in S. There are no isolated vertices in Nin and Nout.
Proof: Since G is acyclic, MSN(D(G), S, T ) is also acyclic. Every vertex in MSN(D(G), S, T ) is in an S-T path in MSN(G, S, T ). Thus this lemma follows from Lemma 2.2 and
Corol-lary 2.3. 2
Corollary 2.6 The number of arborescences in Nin (respectively, Nout) is no more than half
of the number of leaves in Nin (respectively, Nout).
Proof: There is no isolated vertex in Nin or Nout. In each arborescence, there are at least
two leaves. Hence the corollary holds. 2
Now we examine properties of the three disjoint subgraphs in a neutral split network. Note that Nin is a forest. We will exploit properties of an incoming arborescence, denoted
as Nin0 , constructed as follows from Nin Let u be a vertex not in the neutral split network
of MSN(D(G), S, T ). Nin0 is constructed by adding to Nin a new vertex u and an edge from
each root in Nin to u. All new edges have zero weight. Let D(G)0 be the resulting graph
obtained by adding the same set of vertex and edges to D(G).
Lemma 2.7 The graph Nin0 is a minimum Steiner incoming arborescence in D(G)0 and can be obtained in O(nm + `2·n`−t) time, where ` > 2 is the number of leaves in Nin and t the
Proof: It takes O(nm) time to find the distance network for a directed acyclic graph [14]. Note that the distance network contains O(n2) edges. The minimum spanning arborescence
in a graph with x vertices and y edges can be found in O(x· log x + y) time [5]. There are less than `− t Steiner vertices and O(`2) edges in a minimum Steiner arborescence. The number of subgraphs of G with less than `− t vertices is O(n`−t). For each subgraph above, the time to find its minimum spanning arborescence is O((`− t) log(` − t) + `2) = O(`2). Nin0 is a minimum spanning arborescence of a subgraph described above. Hence the lemma
holds. 2
Given Nin0 , Nin can be obtained in time linear in the number of vertices in Nin. It is
also true that Nin is a minimum Steiner incoming arborescence in D(G). Similarly we can
construct an outgoing arborescence Nout0 by adding to Nout a new vertex u and and an edges
from u to each root node in Nout. Let D(G)00 be the resulting graph obtained by adding the
same set of edges to D(G) as in the previous construction. The weight of each added edge is zero.
Lemma 2.8 Nout0 is a minimum Steiner outgoing arborescence in D(G)00and can be obtained in O(nm + `2·n`−t) time, where ` > 2 is the number of leaves in Nout and t the number of
trees in Nout. 2
It can be easily proven that given Nout0 , Nout can be obtained in time linear in the number
of vertices in Nout0 . It is also true that Nout is a minimum Steiner outgoing arborescence in
D(G).
Corollary 2.9 Let `in be the number of leaves in Nin and let `out be the number of leaves in
Nout.
(1) The number of internal vertices in Nin is less than `in.
(2) The number of internal vertices in Nout is less than or equal to `out.
Proof: The degree of each internal vertex in Nin is at least 2. Thus (1) holds by using a
simple induction argument. Note that the degree of the root in a tree in Nout could be one.
Thus (2) holds by using a simple induction argument. 2
2.2
Dynamic Programming Approach
We first give an algorithm that runs in time and space that are both polynomial in n with constant degrees, but are exponential in σ. Our approach is similar to the one used in [3].
Let Y1 ⊆ S and let Y2 ⊆ T . We define two restricted versions of the minimum Steiner
minimum Steiner network under the condition that i must be an internal convergent vertex. Given a vertex i∈ Z ∪ T , let MSN2i(D(G), Y1∪ {i}, Y2) be a minimum Steiner network under
the condition that i must be an internal divergent vertex.
Let W (Y1, Y2) be the total edge weight for MSN(D(G), Y1, Y2). Let Wi1(Y1, Y2) be the
total edge weight for MSN1i(D(G), Y1∪ {i}, Y2). Let Wi2(Y1, Y2) be the total edge weight for
MSN2i(D(G), Y1, Y2∪ {i}).
Let H be a solution for MSN1i(D(G), Y1 ∪ {i}, Y2). Thus the total edge weight of
H is Wi1(Y1, Y2). The split graph of H at i contains two minimum spanning networks
MSN(D(G), Y10,{i}) and MSN(D(G), Y1∪ {i} \ Y10, Y2)}, where Y10 is the subset of vertices in
the component that contains the vertex i. We can obtain a similar formulation for Wi2(Y1, Y2).
We then have the following equations: Wi1(Y1, Y2) = min
∀Y0 1⊂Y1
{W (Y10,{i}) + W (Y1∪ {i} \ Y10, Y2)}, and (1)
Wi2(Y1, Y2) = min ∀Y0
2⊂Y2
{W (Y1, Y2∪ {i} \ Y20) + W ({i}, Y20)}. (2)
Let ai,j be the edge weight between vertices i and j in D(G). To find W ({i} ∪ Y1, Y2),
the optimal solution will be in one of the following four cases depending on the type of vertex. Case 1. i is internally convergent; Wi1(Y1, Y2) is the solution. Case 2. i is internally
divergent; W2
i(Y1, Y2) is the solution. Case 3. i is a leaf and points to a vertex in Y1;
min∀j∈Y1{ai,j + W (Y1, Y2)} is the solution. Case 4. i is a leaf and points to an internal
vertex which makes the vertex pointed to by i an internal convergent vertex; min∀j6∈Y1{ai,j+
W1
j(Y1, Y2)} is the solution. Based on the four cases discussed above, we have the following
formula: W ({i} ∪ Y1, Y2) = min Wi1(Y1, Y2) W2 i(Y1, Y2)
min∀j∈Y1{ai,j + W (Y1, Y2)}
min∀j6∈Y1{ai,j + Wj1(Y1, Y2)} . (3)
Similarly, we derive the following formula.
W (Y1,{i} ∪ Y2) = min W1 i(Y1, Y2) W2 i(Y1, Y2)
min∀j∈Y1{ai,j + W (Y1, Y2)}
min∀j6∈Y1{ai,j + Wj2(Y1, Y2)} . (4)
1. Computer D(G);
2. For each Y1 ⊆ S and each Y2 ⊆ T do
(a) For each vertex i∈ V do i. If i∈ Y1, then
Compute and store W1
i (Y1, Y2) according to Equation 1;
ii. If i∈ Y2, then
Compute and store W2
i (Y1, Y2) according to Equation 2;
iii. Compute W ({i}∪Y1, Y2) using Equation 3 and store the corresponding
minimum Steiner network;
iv. Compute W (Y1,{i}∪Y2) using Equation 4 and store the corresponding
minimum Steiner network;
3. Return minimum Steiner network with the least stored W (S, T ) value.
Let Y10, Y100 ⊆ S and Y20, Y200 ⊆ T . In implementing Step 2, if |Y10| ≥ |Y100| and |Y20| ≥ |Y200|, then the loop body with indexes Y1 = Y100 and Y2 = Y200 is executed before the loop
body with indexes Y1 = Y10 and Y2 = Y20. That is, the loop is executed in the order
of (|Y1|, |Y2|) = (0, 0), (0, 1), (1, 0), (1, 1), (1, 2),(2, 1), . . . , (|S|, |T |). Note that for a fixed
(|Y1|, |Y2|), we execute all possible candidates for Y1 and Y2 in random order.
Given fixed i, Y1 and Y2, it takes O(2|Y1|) (respectively, O(2|Y2|)) computations of the W
function to find Wi1(Y1, Y2) (respectively, Wi2(Y1, Y2)). In total, there are O(n·2σ) different
values for Wi1 and Wi2. Steps 2(a)i and 2(a)ii must compute the W function (n·3σ) times. There are O(n·2σ) formulas of the form Equations 3 or 4. Each of them involves a computation of a minimum of O(n) terms. Hence it takes O(n2·2σ) time to compute all W functions. Overall, Steps 2(a)iii and 2(a)iv take O(n·3σ + n2·2σ) time and O(n·2σ) space.
Note that we need O(nm) time and O(n2) space to compute and store a minimum Steiner
network of a directed acyclic graph [14]. Hence we have the following theorem:
Theorem 2.10 We can find MSN(D(G), S, T ) in O(nm + n·3σ+ n2·2σ) time and O(n32σ)
space. 2
2.3
Enumerating Approach
We now give an algorithm that uses O(n2) space, but runs in time that is polynomial in n
with a degree O(max{α − 2, β − 1}).
Using Lemmas 2.5, 2.7, and 2.8, we can construct a minimum Steiner network as follows. First we obtain (by exhaustive enumeration) S1 ⊆ S and T1 ⊆ T such that |S1| = |T1|, and
construct Nu by finding a minimum-cost bipartite perfect matching between S1 and T1 in
network of MSN(D(G), S, T ). Note thatR can be partitioned into roots which are neither in S nor in T , roots which are in S\S1, and roots which are in T\T1. That is,R = R1∪R2∪R3
where R1 ⊆ V \ (S ∪ T ), R2 ⊆ (S \ S1), and R3 ⊆ (T \ T1). After choosing R, we find a
minimum Steiner incoming forest Nin on the set of leaves S \ (S1 ∪ R) and the set of roots
R \ R2. By Corollary 2.9, there can be at most |S| − |S1| − 1 Steiner vertices (including
vertices in R). We also find a minimum Steiner outgoing forest Nout on the set of leaves
T \ (T1∪ R) and the set of roots R \ R3. By Corollary 2.9, there can be at most |T | − |T1|
Steiner vertices (including vertices inR). Note that the sets of Steiner vertices in Nin and in
Nout are disjoint. Because the way S1, T1, and R are chosen, the cost of MSN(D(G), S, T )
is equal to the cost of Nu∪ Nin∪ Nout. MSN(D(G), S, T ) is easily constructed from Nu, Nin,
and Nout. The algorithm for the above discussion is as follows.
1. Compute D(G);
2. For each S1 ⊆ S, T1 ⊆ T and |S1| = |T1| = i do
(a) Compute and store Nu formed by a minimum-cost bipartite matching
be-tween S1 and T1 in D(G);
(b) For each R ⊆ V and j = |R| ≤ α − i do
i. LetR2 =R∩(S \S1), letR3 =R∩(T \T1) and letR1 =R\(R1∪R2);
ii. For each W ⊆ V and |W | ≤ |S| − i − j − 1 do
• Compute a minimum Steiner incoming forest on the set of leaves S \ (S1 ∪ R, the set of internal vertices W and the set of roots
R1∪ R3;
Let Nin be a forest with the least cost among all forests found above;
iii. For each W ⊆ V and |W | ≤ |T | − i − j do
• Compute a minimum Steiner outgoing forest on the set of leaves S \ (T1 ∪ R, the set of internal vertices W and the set of roots
R1∪ R2;
Let Nout be a forest with the least cost among all forests found above;
(c) Make Nin∪ Nout∪ Nu a candidate for MSN(D(G), S, T );
3. Return a solution with the least total edge weight among all candidates. From the above discussion, we have the following theorem:
Theorem 2.11 MSN(G, S, T ) can be constructed in O(nm + 2σ·α3·(nα−2+ nβ−1)) time and O(n2) space.
Proof: Without loss of generality assume that α = |S| and β = |T |. Note that |S1| =
|T1| ≤ β. Our algorithm first constructs the distance network (Step 1). We then
each candidate has been enumerated, we record its total weight. After all candidates have been enumerated, any one that has the minimum total weight is a solution we want. By Lemma 2.5, a candidate solution can be partitioned into the three disjoint networks Nu, Nin
and Nout. Hence we construct all possible candidate solutions by using all possible choices
for Nu, Nin and Nout. By using properties proven in the previous section, we can greatly
reduce the number of choices for Nu, Nin and Nout.
Let i be the number of pairs of vertices in Nu. Note that i ≤ β. Hence there are up to
|S| i ! |T | i !
possible different choices for the set of vertices in Nu.
Recall the definition of R in the neutral split network of MSN(D(G), S, T ). Let |R| = j. By Corollary 2.6, j ≤ jα−i2 k+jβ−i2 k, which is no more than α− i. There are up to n
j
!
candidates for the set of vertices R. Once we pick R, we partition R into R1, R2 and R3
as specified in Step 2(b)i. Note that the set of vertices in Nin is R1 ∪ R3 ∪ (S \ R2) and
the set of vertices in Nout is R1 ∪ R2 ∪ (T \ R3). We enumerate choices for Nin and Nout
by enumerating the choices for R and then finding minimum Steiner forests as specified in Steps 2(b)ii and 2(b)iii.
Thus our algorithm takes time
O((A) + β X i=1 |S| i ! |T | i !α−i X j=1 n j ! [(B) + (C) + (D)]),
where (A) is the time needed to construct the distance network (Step 1) from G and is equal to O(nm) for a directed acyclic graph [14]; (B) is the time needed to find a minimum cost bipartite perfect matching in a bipartite graph (Step 2a) with 2·i vertices and O(i2)
edges and is O((2·i)2log(2·i) + (2·i)·i2) [4]; (C) is the time needed to find a minimum Steiner
incoming forest with j roots, |S| − i leaves, and up to |S| − i − j − 1 internal vertices given D(G) (Step 2(b)ii); and (D) is the time needed to find a minimum Steiner outgoing forest with j roots, |T | − i leaves, and up to |T | − i − j internal vertices given D(G) (Step 2(b)iii). By Lemmas 2.7 and 2.8, we know that (C) is O(|S|2·n|S|−i−j−1) and (D) is O(|T |2·n|T |−i−j).
Thus (B)+(C)+(D) = O(α2·(nα−i−j−1+ nβ−i−j)).
Since n j ! ≤ nj, n j !
((B) + (C) + (D)) = O(α2·(nα−i−1+ nβ−i)).
Thus α−i X j=1 n j !
((B) + (C) + (D))) = O(α3·(nα−i−1+ nβ−i)).
Since β X i=1 |S| i ! |T | i ! ≤ β X i=1 β i ! α X i=1 α i ! and α X i=1 α i ! = 2α− 1,
β X i=1 |S| i ! |T | i ! = O(2α·2β).
Thus, the overall time complexity is O(nm + 2σ·α3·(nα−2+ nβ−1)). It takes O(n2) space to
store the distance network. Hence the theorem holds. 2
By Lemma 2.4, the number of Steiner vertices in a minimum Steiner network can be as large as σ− 2. Finding a minimum Steiner network by brute force may require doing a min-imum spanning arborescence computation O(n|σ−2) times. From Theorem 2.11 it appears that a minimum Steiner network can be found by performing a minimum spanning arbores-cence computation O(2σ·α}·(nα−2+ nβ−1)) times. This substantially saves computation time
if α is O(log n).
Remark: Within the same time complexity, we can solve the strong minimum Steiner network problem in which no intermediate vertices in any S-T path can belong to S and T . In other words, all starting vertices are of in-degree 0 (sources) and all terminating vertices are of out-degree 0 (sinks). This problem can be solved by finding MSN(G0, S, T ) where G0 is obtained by removing all incoming edges to a starting vertex and all outgoing edges to a terminating vertex.
Within the same time complexity, we can also solve the MSN problem on an undirected graph, in which each S-T path in the solution is undirected, by applying the algorithm in Sections 2.2 and 2.3. The correctness of the algorithm, which is established in properties proved in Section 2.1 for the directed case, can be applied to our algorithm for the undirected case as well. Observe that a solution for an undirected minimum Steiner network contains no cycles. Thus there is a unique orientation for the undirected solution by orienting edges in every S-T path from a vertex in S towards a vertex in T . All properties in Section 2.1 can be applied to this oriented solution.
2.4
A Linear Time Algorithm When α = 2 and β = 1
Note that if β = 1, then finding a minimum Steiner network is equivalent to finding a
minimum Steiner arborescence. Let the (i, j)-MSN problem denote the MSN problem
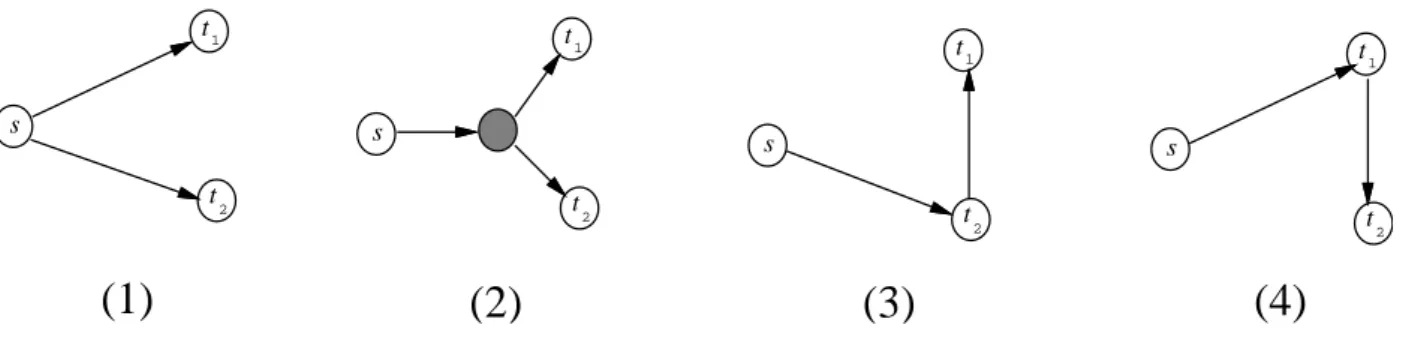
with i starting vertices and j terminating vertices. In Figure 2, we list the four possible configurations for the (1,2)-MSN problem.
For the solving the MSN problem in which α = 2, the following result shows that the computation of the distance network can be avoided when |S ∪ T | = 3.
Theorem 2.12 If β = 1 and α = 2, then MSN(G, S, T ) can be computed in O(n + m) (instead of O(n·m)) time and O(n + m) (instead of O(n2)) space.
s t1 t 2 s t1 t 2 s t1 t 2 s t1 t 2
(1)
(2)
(3)
(4)
Figure 2: All possible configurations for a solution of the (1,2)-MSN problem in the distance network where the starting vertex is s and the set of terminating vertices is {t1, t2}. The
shaded vertex is a Steiner vertex.
Proof: Note that there is at most one Steiner vertex in MSN(D(G), S, T ). Any path from any vertex u to another vertex v in MSN(G, S, T ) is also a shortest path from u to v in G. Without loss of generality assume that |S| = 1 and |T | = 2. Our algorithm first computes the single source shortest paths (in G) for the vertex in S. Let r(G) be the resulting graph obtained by reversing the direction of each edge in G. We then compute the single source shortest paths (in r(G)) for each of the two vertices in T . The above computation takes O(m) time for a directed acyclic graph.
We distinguish two cases.
Case 1: There is no Steiner vertex.
The cost of a minimum Steiner network is equal to the sum of edge-costs in the two paths from the vertex in S to the two vertices in T (Figure 2.(1)), or in the one path from the vertex in S to the two vertices in T (Figures 2.(3) and 2.(4)).
Case 2: There is exactly one Steiner vertex u.
Note that u could be a vertex in T and that this case reduces to those shown in Figures 2.(3) and 2.(4). We can try all possible candidates for u. Whenever we fix a candidate for u, the cost of the Steiner network with only one Steiner vertex u can be computed in constant time by adding the shortest path distance (in G) from the vertex in S to u, and the costs of the two shortest paths (in r(G)) from the two vertices in T to u.
Hence the theorem holds. 2
Remark: We can also solve in linear time and space the MSN problem on an undirected graph in which each S-T path in the solution is undirected by using the same algorithm.
3
The Minimum Union Paths Problem
Given a weighted directed acyclic graph G = (V, E) and three non-empty mutually disjoint subsets of vertices S, H, and T , a set of S-H-T union paths of G is a subgraph G0 of G with the following properties.
1. For every s ∈ S there is a path in G0 from s to a vertex in T . 2. For every t∈ T there is a path in G0 from a vertex in S to t.
3. For every h∈ H there is a path in G0 passing through h which starts from some vertex in S and ends with some vertex in T .
The set of vertices S is referred to as starting vertices, the set of vertices H as hitting vertices and the set of vertices T as terminating vertices. The minimum union paths problem is to find a set of S-H-T minimal union paths in G with a minimum total edge weight.3 A set of
minimum union paths that has the minimum total edge weight is MUP(G, S, H, T ).
Lemma 3.1 There are at most γ + |H| − 4 Steiner vertices in MUP(D(G), S, H, T ) for |H| ≥ 1.
Proof: We prove this lemma by induction on γ +|H|. Note that γ + |H| = |S| + |T | + 2·|H|. This lemma is trivially true when |S| = 1, |T | = 1 and |H| = 1. For the induction step, we observe that adding a vertex to S or T creates at most one Steiner vertex and that adding
a vertex to H creates at most two Steiner vertices. Hence the lemma is true. 2
Similar to Lemma 2.1 we have the following.
Lemma 3.2 MUP(G, S, H, T ) can be constructed from MUP(D(G), S, H, T ) in linear time
and space. 2
If |S| > 1 or |T | > 1, then we augment the given graph by adding to G two new vertices s0 and t0 and the set of edges E∗ = {(s0, s) | s ∈ S} ∪ {(t, t0) | t ∈ T }. The edge weight
of each added edge is an arbitrary positive constant. Let ˜G be the augmented graph. From MUP( ˜G,{s0}, S ∪ H ∪ T, {t0}) we can obtain the solution MUP(G, S, H, T ) by deleting the
vertices s0 and t0 and all their incident edges. Henceforth, without loss of generality we may
assume that |S| = |T | = 1 and we also consider the distance network D(G) of G.
3Here we also consider the network with the smallest number of edges among those that have a minimum
3.1
Preliminaries
Before we present a solution to MUP(D(G),{s}, H, {t}), we first discuss properties of an optimal solution. Given MUP(D(G),{s}, H, {t}), note that s has no incoming edge and t has no outgoing edge. Let Li denote the subset of vertices in H such that for every vertex
v ∈ Li there is a path from s to v containing at most i vertices in H. Note that when we
traverse any path from s to t in MUP(D(G),{s}, H, {t}), the first vertex in H encountered is in L1. Let ` be the smallest integer such that L` = L`+1. Then MUP(D(G),{s}, H, {t})
has ` levels.
According to the definition of Li, we partition H as follows. Let H1 = L1 and Hi =
Li\ Li−1 for all 2≤ i ≤ `. Let H0 ={s} and let H`+1 ={t}.
Lemma 3.3 It is not possible to have a path in MUP(D(G),{s}, H, {t}) from a vertex in
Hi to a vertex in Hj, if i + 1 < j and j6= ` + 1. 2
A vertex v ∈ Hi is backward if there is a path Pv,v∗ 0 from v to a vertex v0 ∈ Hj, j ≤ i,
that does not pass through any other vertex in H. The vertex v0 is a backward successor of v. Pv,v∗ 0 is called a backward path. A vertex v ∈ Hi is forward if there is a path Pv,t∗ from v
to t that does not pass through any other vertex in H. Pv,t∗ is called a forward path. The following lemma states that a vertex cannot be both forward and backward. Furthermore, there is at most one forward or backward path.
Lemma 3.4 For any vertex in H there exists at most one forward or one backward path, but not both.
Proof: If a vertex v is both forward and backward, let Pf and Pb be its forward and backward
paths, respectively. Let e = (x, y) be the first edge, not contained in Pb, encountered when
we traverse Pf starting from v. Since t has no outgoing edge, e must exist. Let G0 be the
graph resulting from removing edge e from MUP(D(G),{s}, H, {t}). For a {s}-{t} path P in MUP(D(G),{s},H,{t}) that passes through e, we can find an {s}-{t} path P0 in G0 by unioning: (1) sub-path of P from s to x, (2) sub-path of Pb from x to the backward
successor u of v, and (3) any path from u to t. Thus G0 is a set of {s}-H-{t} union paths with a smaller total edge weight or a smaller number of edges than MUP(D(G),{s}, H, {t}). This is a contradiction. Thus we know v cannot be both forward and backward.
We now suppose that v has two backward paths P1 and P2. Let e be the first edge, not
contained in P2, encountered when we traverse P1 starting from v. Then by an argument
similar to the one given in the last paragraph, we can derive a contradiction. Similarly one
can prove that it is impossible for v to have more than one forward path. 2
1 2 3 4 5 8 9 10 11 12 13 14 6 7 15 16 17 18 19 20
H
1H
2H
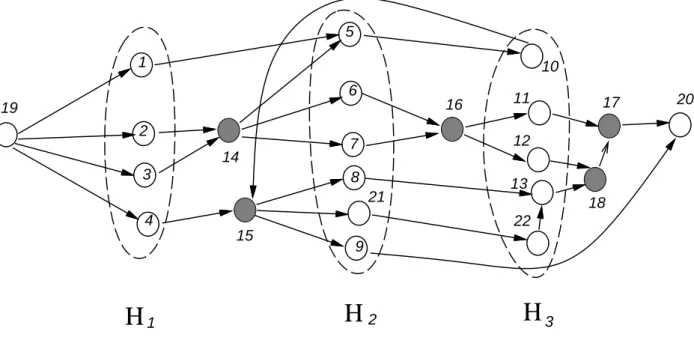
3 21 22Figure 3: A set of minimum union paths on the starting vertex set {19}, the hitting vertex set {1,2,3,4,5,6,7,8,9,10,11,12,13,21,22} and the terminating vertex set {20}. The hitting set is partitioned into H1 ={1, 2, 3, 4}, H2 ={5, 6, 7, 8, 9, 21} and H3 ={10, 11, 12, 13, 22}.
Vertex 10 is a backward vertex whose backward index is 1. Vertex 22 is also a backward vertex whose backward index is 2. Vertex 9 is a forward vertex.
Let Hf (respectively, Hb) be the set of forward (respectively, backward) vertices in H.
Let Hi0 be the set of vertices in Hi that is neither forward nor backward. We define a split
extension graph for MUP(D(G),{s}, H, {t}) as follows. For every vertex u ∈ (Hf ∪ Hb), we
split u into two vertices uin and uout where uin inherits all incoming edges and uout inherits
all outgoing edges. The rest of the edges and the vertices remain unchanged.
Given a backward vertex u whose backward successor is in Hi, its backward index bi(u)
is i− 1. The backward index of a forward vertex is ` and the backward index of a vertex that is neither forward nor forward is ∞. The level index of u, `i(u) = i if u ∈ Hi. We
partition edges in the split extension graph for MUP(D(G),{s}, H, {t}) into G0∪G1∪· · ·∪G`
where Gi is the induced subgraph of MUP(D(G),{s}, H, {t}) on the two sets of vertices
Hi = Hi0 ∪ {uout | bi(u) = i} and Hi = Hi+10 ∪ {uin | `i(u) = i + 1}. The sets of vertices
H0, H1, . . . , H`, and H0, H1, . . . , H` are the pairwise extension of H0, H1, . . . , and H`+1.
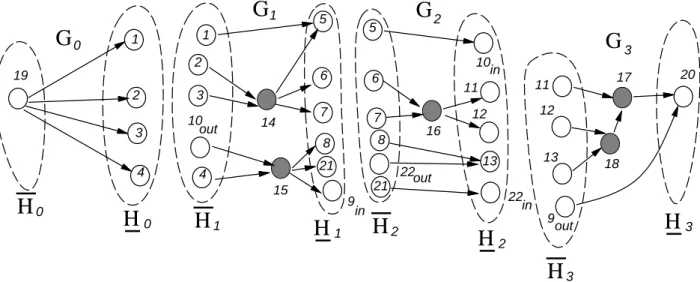
In Figure 4, we illustrate an example of the pairwise extension of the set of minimum union paths in Figure 3.
Lemma 3.5 Gi is a minimum Steiner network MSN(G, Hi, Hi).
Proof: Note that Gi is a directed Steiner network in G for the set of starting vertices Hi
11 12 13 14 5 8 9 6 7 15 16 17 18 20 1 3 4 19 4 3 2 2 5 8 9 6 7 10 11 12 13
G
0G
1G
2G
3H
1H
2H
0H
0H
1H
2H
3H
3 10 out in in out 1 21 21 22 out 22 inFigure 4: The pairwise extension and the split partition graphs of the minimum union paths shown in Figure 3.
be a minimum Steiner network. We delete edges in Gi from MUP(D(G),{s}, H, {t}) and
replace them with edges in G0i. We obtain a set of union paths with either smaller total edge
weights or a smaller number of edges. This is a contradiction. 2
3.2
The Algorithms
Given MUP(D(G),{s}, H, {t}), we define its configuration to be the pairwise extension of H0, H1, . . . , and H`+1. By Lemma 3.5, we can find an MUP(D(G),{s}, H, {t}) as follows. We
first find its configuration, then we construct each Gi by using the algorithms in Sections 2.2
and 2.3 to find a minimum Steiner network. Our algorithm finds the correct configuration by enumerating all possible configurations given H.
Lemma 3.6 There are O(k!·2k·kk) possible configurations for MUP(D(G),{s}, H, {t}), where
k =|H|.
Proof: Let T (k) be the number of different ways that one can partition a set of k vertices. Then T (0) = 0 and T (k) = k X i=1 k i ! ·T (k − i).
Thus, T (k) = O(k!·2k). Given a partition for H, each vertex in H can be either a forward
vertex, a backward vertex, or a vertex that is neither forward nor backward. The backward index of a backward vertex can also have `− 1 choices. However, the total number of choices is less than or equal to k. Thus there are O(kk) different pairwise extensions for a partition.
Theorem 3.7 MUP(D(G),{s}, H, {t}) can be found in either O(nm+k!·n((18·k)k+n·(8k)k))
time and O(n3·4k) space, or O(k!·(8·k)k·k3·nk−1+nm) time and O(n2) space, where k =|H|.
Proof: Algorithm for implementing this theorem is as follows. 1. Compute D(G);
2. /∗ Enumerate all possible configurations. ∗/
For each possible partition (H1, H2, . . . , H`) of H do
(a) For each possible combination of backward indices of vertex in H do i. construct the corresponding pairwise extension H0, H1, . . . , H`,
H0, H1, . . . , and H`; ii. For each i ≤ ` do
• Compute Gi = MSN(D(G), Hi, Hi);
iii. Make G0∪ G1∪ · · · ∪ G` a candidate for MUP(D(G),{s}, H, {t});
3. Return a solution with the least total edge weight found among all candidates. Note that|Hi| ≤ k and |Hi| ≤ k for all 0 ≤ i ≤ `. Note also that |∪`i=0(Hi∪Hi)| ≤ 2k+2.
Given a partition extension of a partition of H, the time and space needed in Step 2(a)ii to compute all Gi is bound by computing (k, k)-MSN which are either O(nm + n·32k+ n2·22k)
time and O(n3·22k) space by Theorem 2.10, or O(4k·k3·nk−1+ nm) time and O(n2) space by Theorem 2.11, where O(nm) is the time to compute the distance network. Given G, the distance network for G needs only be computed once. The number of times that Step 2a
being executed is analyzed in Lemma 3.6. Hence the theorem holds. 2
Theorem 3.8 MUP(D(G), S, H, T ) can be found in Either O(nm + γ!·n((18·γ)γ+ n(8γ)γ)) time and O(n3·4γ) space, or O(γ!·(8·γ)γ·γ3·nγ−1+ nm) time and O(n2) space.
Proof: By Lemma 3.2 and Theorem 3.7. 2
By Lemma 3.1, the number of Steiner vertices in a minimum Steiner network can be as large as γ +|H| − 4. Finding a minimum Steiner network by brute force may require doing a minimum spanning arborescence computation O(nγ+|H|−4) times. Theorem 3.8 states that by using our algorithm, a set of minimum union paths can be found by performing a minimum spanning arborescence computation O(γ!·(8·γ)γ·γ·nγ−1) times. For a fixed γ our algorithm runs in O(nm + nγ−1) time, while a brute force approach takes O(nm + nγ+|H|−4) time. Thus our algorithm runs asymptotically faster when |H| is a constant greater than 3.
3.3
A Linear Time Algorithm When
|S| = |T | = 1 and |H| = 2
Let the (i, k, j)-MUP problem denote the MUP problem with i starting vertices, k hitting vertices and j terminating vertices. In this section, we give a linear-time-and-space algorithm
s t h1
h
2
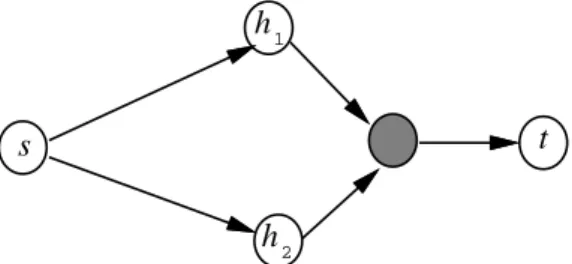
Figure 5: A possible solution for the (1,2,1)-MUP problem in the distance network where the starting vertex is s, the terminating vertex is t and the set of hitting vertices is{h1, h2}.
The shaded vertex is a Steiner vertex.
to solve the (1,2,1)-MUP problem. Note that the original algorithm needs to compute a distance network and thus takes at least O(nm) time. We will show that the computation of the distance network can be avoided as in Section 2.4 for the (1,2)-MSN problem.
We first analyze all possible configurations of a solution for the (1,2)-MSN problem when there is one starting vertex and two terminating vertices. As shown below, the solution for the (1,2,1)-MUP problem can be decomposed into the union of solutions to two instances of the (1,2)-MSN problem.
In Figure 2, we list the four possible configurations for the (1,2)-MSN problem. The solution for the (1,2,1)-MUP problem can be easily obtained by the union of solutions to two (1,2)-MSN problems. For example, the solution in Figure 5 is a union of type (1) in Figure 2 and the graph obtained from type (2) in Figure 2 after reversing the directions of edges. Note that if the first part of the solution is type (3) or (4) in Figure 2, we only have to find a path from a hitting vertex to the terminating vertex to form a desired solution.
Thus, to find the solution for the (1,2,1)-MUP problem with one starting vertex s, two hitting vertices h1 and h2 and one terminating vertex t, we first find MSN(G,{s}, {h1, h2}).
By Theorem 2.12, this can be done in linear time and space. According to the discussion in Section 3.1, the set H of hitting vertices can be partitioned into at most two levels.
We distinguish two cases.
Case 1: The hitting vertices are in the same level.
This occurs when MSN(G,{s}, {h1, h2}) is either type (1) or (2) in Figure 2. Let
r(G) be the resulting graph obtained from G by reversing the direction of each edge in G. We find MSN(r(G),{t}, {h1, h2}). Since both MSN(r(G), {t}, {h1, h2}) and
MSN(G,{s}, {h1, h2}) are optimal solutions and G is acyclic, no vertex other than h1
and h2 can appear in both MSN(r(G),{t}, {h1, h2}) and MSN(G, {s}, {h1, h2}).
we want is MSN(G,{s}, {h1, h2}) ∪ r(MSN(r(G), {t}, {h1, h2})). If MSN(r(G), {t},
{h1, h2}) is either type (3) or (4) in Figure 2, without loss of generality, let h1 be the
vertex with in-degree 0 in r(MSN(r(G),{t}, {h1, h2})). A shortest path from s to h1
together with r(MSN(r(G),{t}, {h1, h2})) is the desired solution.
Case 2: The two hitting vertices are in different levels.
This occurs when MSN(G,{s}, {h1, h2}) is either type (3) or (4) in Figure 2. Without
loss of generality, let h1 be the hitting vertex whose out-degree is 0 in
MSN(G,{s}, {h1, h2}). We complete the computation by finding a shortest path from
h1 to t.
Hence we have the following theorem.
Theorem 3.9 The (1,2,1)-MUP problem can be solved in linear time and space. 2
Remark: When |H| is small, enumerating all possible partitions of H is an effective way to find a solution for the MUP problem.
4
Concluding Remarks
We have described an enumerative approach to solve two variations of the minimum-cost Steiner problem on a directed acyclic graph with non-negative edge weights. Properties of the solutions were presented and used to obtain algorithms more efficiently than brute force enumerating methods for these two problems. Whether or not additional properties of the graph can be used to improve the time complexity of the algorithms that compute optimal solutions remains to be seen.
References
[1] Y. P. Aneja. An integer linear programming approach to the Steiner problem in graphs. Networks, 10:167–178, 1980.
[2] G. Dahl. Directed Steiner problems with connectivity constraints. Discrete Applied Math., 47:109–128, 1993.
[3] S. E. Dreyfus and R. A. Wagner. The Steiner problem in graphs. Networks, 1:195–207, 1972.
[4] M. L. Fredman and R. E. Tarjan. Fibonacci heaps and their uses in improved network optimization algorithms. Journal of ACM, 34(3):596–615, 1987.
[5] H. N. Gabow, Z. Galil, T. Spencer, and R. E. Tarjan. Efficient algorithms for finding minimum spanning trees in undirected and directed graphs. Combinatorica, 6(2):109– 122, 1986.
[6] S. L. Hakimi. Steiner’s problem in graphs and its applications. Networks, 1:113–133, 1971.
[7] T.-s. Hsu, K.-H. Tsai, D.-W. Wang, and D. T. Lee. Steiner problems on directed acyclic graphs. In J. Y. Cai and C. K. Wong, editors, Lecture Notes in Computer Science 1090: Proceedings of the 2nd International Symposium on Computing and Combina-torics, pages 21–30. Springer-Verlag, New York, NY, 1996.
[8] F. K. Hwang and D. S. Richards. Steiner tree problems. Networks, 22:55–89, 1992. [9] F. K. Hwang, D. S. Richards, and P. Winter. The Steiner Tree Problem. Annals of
Discrete mathematics 53. North-Holland, 1992.
[10] E. L. Lawler. Combinatorial Optimization: Networks and Matroids. Holt, Rinehart, and Winston, New York, 1976.
[11] S. Martello and P Toth. Finding a minimum equivalent graph of a digraph. Networks, 12:89–100, 1982.
[12] L. Nastansky, S. M. Selkow, and N. F. Stewart. Cost-minimal trees in directed acyclic graphs. Zeitschrift f¨ur Operations Research, pages 59–67, 1974.
[13] S. K. Rao, P. Sadayappan, F. K. Hwang, and P. W. Shor. The rectilinear Steiner arborescence problem. Algorithmica, pages 277–288, 1992.
[14] R. E. Tarjan. Data Structures and Network Algorithms. SIAM Press, Philadelphia, PA, 1983.
[15] S. Voss. Worst-case performance of some heuristics for Steiner’s problem in directed graphs. Information Processing Letters, 48:99–105, 1993.
[16] P. Winter. Steiner problem in networks: A survey. Networks, 17:129–167, 1987.
[17] R. T. Wong. A dual ascent approach for Steiner tree problems on a directed graphs. Mathematical Programming, 28:271–287, 1984.