撓性連桿機械臂之適應控制研究

行政院國家科學委員會專題研究計畫 成果報告

撓性連桿機械臂之適應控制研究

計畫類別： 個別型計畫

計畫編號： NSC91-2212-E-011-050-

執行期間： 91 年 08 月 01 日至 92 年 07 月 31 日 執行單位： 國立臺灣科技大學機械工程系

計畫主持人： 黃安橋

報告類型： 精簡報告

處理方式： 本計畫可公開查詢

中 華 民 國 92 年 9 月 8 日

行政院國家科學委員會專題研究計畫成果報告 撓性連桿機械臂之適應控制研究

Adaptive Contr ol for Flexible Ar ms Using Function Appr oximation Technique

計畫編號：NSC 91-2212-E-011-050 執行期限：91 年 8 月 1 日至 92 年 7 月 31 日 主持人： 黃安橋 國立台灣科技大學機械系

中文摘要

本計畫針對一具有未知時變參數且未知邊界值之單軸撓性連桿機械臂，提出適應性滑動控 制法則，以改善傳統滑動控制需知道未知參數之邊界值的限制，並且以正交函數之有限組合進行 時變未知參數的近似。故在改變端點負載及系統參數全部未知條件下，亦可達到端點快速定位控 制的目的。電腦模擬，以及實驗結果顯示，本計畫所提出之控制器確實可達到期望之性能。

關鍵字：適應控制，撓性連桿機械臂，函數近似。

Abstr act

An adaptive controller is proposed in this project for flexible arms containing time varying uncertainties with unknown bounds based on the function approximation technique. The uncertainties are firstly represented by finite linear combinations of orthonormal basis with some unknown constant weighting vectors. Output error dynamics can thus be derived as a stable first order filter driven by parameter error vectors. Appropriate update laws for the weighting vectors are selected using the Lyapunov method so that asymptotic convergence of the output error can be proved as long as a sufficient number of basis functions are used. Effects of the approximation error on system performance are also investigated in this project. Computer simulation and experimental results confirm the feasibility of the proposed control strategy.

Keywor ds: Flexible arm, Adaptive control, Function approximation

1. Intr oduction

Conventional industrial robots are mostly designed with heavy links to reduce vibration and increase motion accuracy. Although this simplifies controller design, heavy links imply slower response and higher energy consumption. In recent years, development of lightweight robot manipulators has attracted much attention in the literature. With reduced weight, we have to consider flexibility of the links. Since a flexible link has infinitive number of vibration modes, it is impossible to feedback all of them to have a stabilizing controller. A feasible approach is to consider only a few significant modes and treat all others as uncertainties. Therefore, to design a practical controller for a flexible arm, these uncertainties should be carefully considered.

Gokasan et. al. (1998) implemented a DSP-based sliding controller for a flexible arm to achieve robust performance against unmodeled dynamics and parameter variations. Chen et al. (1999) and Chen and Fukuda (2001) regarded higher order vibration modes and friction forces as bounded disturbances and a sliding controller was introduced to stabilize the system. Karandikar and Bandyopadhyay (2000) used a sliding controller to drive a flexible arm to the vicinity of the target position and then a controller based on the linearized model was applied to damp the vibration. Kwok and Lee (2001) suggested to impose a fuzzy-like weighting factor on the sliding-based control signal such that the tracking control component has higher priority when the output error is large, and suppression of vibration is effective when the tracking error is small. Gu and Asokanthan (1999) designed a hybrid controller based on Lyapunov approach generating control actions to the hub motor and distributed piezoelectric film actuator for a flexible arm. Hissenine and Lohmann (2001) implemented two robust controllers: one is based on the sliding control and the other is on the nonlinear H_∝ theory. It was concluded that the later method suffered from computational complexity, although closed-loop stability as well as disturbance attenuation could be achieved. A robust LQ controller was proposed by Ryu et al. (1999) for dealing with a large time varying payload and parameter uncertainties. The system was formulated in the descriptor form with additive uncertainties in polytopic representation. The optimal robust performance was obtained based on the LMI theory.

Bai et la. (1998) presented an adaptive augmented state feedback controller for the tracking control for a two-link flexible robot. Feliu et al. (1999) proposed an adaptive scheme for a flexible

robot with uncertain payload. Instead of calculating the entire transfer function of the system, their method required only the estimation of the tip load but with acceleration feedback. Queiroz et al. (1999) suggested an adaptive nonlinear boundary controller consisting of a boundary control torque applied to the hub and a boundary control force at the tip. A shear force sensor, however, was needed to be installed at the free-end. Rokui and Khorasani (2000) used output redefinition technique to obtain stable internal dynamics for a flexible arm and then an indirect adaptive linearizing controller was developed for updating unknown payload. Cheong et al. (2001) separated the system dynamics into rigid and flexible parts using bandwidth modulation approach. An adaptive controller was designed for the flexible subsystem to arrive at fast vibration suppression. An adaptive energy-based robust controller was designed for multi-line flexible robots in Ge et al. (2001). Desired performance was achieved with automatic gain tuning in some controller component. Direct and indirect adaptive command shaping designs for flexible arms were analyzed in Rhim and Book (2001). The direct approach was shown to be less sensitive to the noise effect on the performance.

Similar to most conventional robust designs, all robust approaches reviewed above have a common assumption that all uncertainties should be defined in some known bounded sets. On the other hand, similar to most adaptive schemes, all adaptive approaches mentioned above require that uncertain parameters be time invariant or slowly time variant. Because lower frequency vibration modes are used to approximate system dynamics, it is generally not easy to know exact variation bounds of the neglected dynamics; therefore robust designs are hard to apply. Since these uncertainties are time variant, implementation of most adaptive controls are not easy either. In this project, we propose an adaptive controller for flexible arms containing time varying uncertainties with unknown bounds using the function approximation technique (Huang and Kuo 2001, Huang and Chen 2002). These uncertainties are firstly represented by finite linear combinations of orthonormal basis with some unknown constant weighting vectors. Output error dynamics can thus be derived as a stable first order filter driven by parameter error vectors. Appropriate update laws for the weighting vectors can be selected so that the time derivative of some Lyapunov function candidate can be proved to be negative semi-definite. Effects of the approximation error on system performance can also be investigated.

This report is organized as follows: Section 2 presents a discretized model of the flexible arm. An adaptive controller is designed in section 3 with rigorous proof of closed loop stability. Section 4 introduces experiment setup and presents results of computer simulations and experiments. Section 5 concludes this report.

2. SYSTEM MODEL

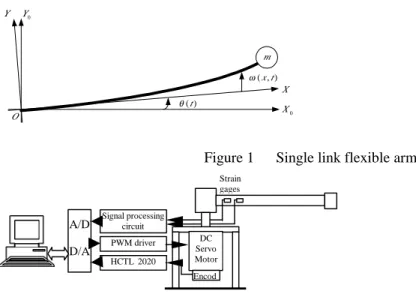
The system under consideration is illustrated in Figure 1. The Euler-Bernoulli beam is clamped to an actuator hub which can rotate in horizontal plane. The payload at the free-end is modeled as a concentrated mass. For an angular displacement θ(t) of the actuator hub at timet≥0, the arm will have a displacement w(x,t) at position x with respect to the (X,Y) coordinate rotating with the hub.

Therefore, the motion of a point along the beam is given by )

, ( ) ( ) ,

(xt x t w xt

y = θ + (1)

It is well-known that using the Lagrange’s method, the flexible arm can be described by a partial differential equation

2 2 2

2 4

4 ( , ) ( , )

x t t

t x y x

t x EI y

∂

− ∂

∂ = + ∂

∂

∂ ρ ρ θ (2)

with four boundary conditions (Meirovitch 1967). The quantity EI is the bending stiffness of the arm and ρ is the mass density. The elastic deformation w(x,t) can be approximated using the assumed mode method as

∑

= ⁿ

i

i i x q t t

x w

1

) ( ) ( ) ,

( φ ⁽³⁾

where φ_i(x) ^{is the} i-th mode shape function and q_i(t) is the i-th generalized coordinate. In this report, we consider only the first two vibration modes, i.e., n=2; therefore, the equation of motion can be further simplified to

u b x f x x

M( )&&+ ( )= (4)

where x=[θ q₁ q₂]^T, b=[0 0 1]^T , f(x)=[k₁₁q₁+k₂₂q₂ k₂₁q₁+k₂₂q₂ 0]^T and

















+ +

+

+ +

+

+ +

+

=

2 02 1 01 00

2 2 22 1 2 21 2 02

2 1 12 1 1 11 1 01

) (

φ φ

φ φ φ

φ φ

φ φ φ

φ φ

ml m ml m ml m

m m m m ml m

m m m

m ml m x M

with ^{m =}

∫

00 ρ , m0_i ⁼

∫

∫

∫

3. ADAPTIVE CONTROLLER DESIGN

In this section we would like to derive an adaptive controller for a flexible arm with time varying uncertainties based on the function approximation approach. We firstly ignore the approximation error by assuming a sufficient number of orthonormal functions are used. Under this condition, the output error can be proved to have asymptotic convergence performance. Afterwards the approximation error is considered, and boundedness of the output error can be concluded. The bound is proved to be a function of the approximation error. Finally, we consider the case when the approximation error bound is available. By including a robust term in the control input, asymptotic convergence of the output error can again be derived.

Let y=c^Tx be the tip position of the flexible arm represented by equation (4), where c∈ℜ³ is a known constant vector. Therefore, the output error can be denoted as e= y−y_d, where yd

represents the desired output. Define a sliding surface as

=0 +

=e e

s ^& λ (5)

The positive constant λ determines the convergent rate of the output error on the sliding surface. Since in generals(0)≠0, we would like to design a controller so that s=0 is attractive. Let us consider the dynamics of s(t) for all t≥0 as

e y

s&=(c^T&x&−&&_d)+λ& (6)

Using (4), the above equation can be rewritten as e

y u g u g g f

s&= +( − ˆ) + ˆ −&&_d+λ& (7)

where f =−c^TM⁻¹f, g=c^TM⁻¹b are unknown time functions and gˆ is an estimate of g. Note that the inertia matrix is non-singular for all t≥0. If an estimate of f is also available, and gˆ is nonsingular for all t≥0, then a controller can be designed to be

ˆ ) ˆ(

1 f y e s

u= g − +&&_d−λ&−η η>0 ⁽⁸⁾

In practical implementation, some projection modification should be applied (Ge et al. 1998, Ioannou and Sun 1996) to avoid singularity of gˆ . With this controller, equation (7) becomes

u g g f f s

s^&=−η +( − ˆ)+( − ˆ) (9)

This implies that s is an output of a stable first order filter driven by approximation errors of f and g. If some proper update laws can be found so that fˆ→ f and gˆ→g , then e→0 can be concluded from (9) and (5). Since f and g are functions of time, traditional adaptive controllers are not applicable.

On the other hand, since their variation bounds are not given, robust designs are not feasible either.

Here, we would like to use the function approximation technique (Huang and Kuo 2001, Huang and

Chen 2002) to representf, g,fˆ andgˆ as

f T

f =wfz (10a)

g T

g=wgz (10b)

f T

fˆ=wˆfz (10c)

g T

gˆ=wˆgz (10d)

Therefore (9) can be rewritten as u s

s^&=−η +w~^T_fz_f +w~^T_gz_g (11)

where w~_f =w_f −wˆ_f and w~_g =w_g−wˆ_g. Since w_f and w_g are constant vectors, their update laws can be easily found by proper selection of a Lyapunov function. Let us consider a candidate as

g g T g f f T

s f

V w Q w w~ Q w~

2

~ 1

~ 2 1 2 1 ₂

+ +

= (12)

where Q_f and Q_g are positive definite matrices with proper dimensions. Taking the time derivative of V along the trajectory of (11), we have

ˆ )

~ ( ˆ )

~ (

~ ˆ

~ ˆ

~ ) ( ~

2

g g g T g f f f T

f

g g T g f f T

f g T g f T

f

su s

s

u s

s V

w Q z w w Q z w

w Q w w Q w z w z w

&

&

&

&

&

− +

− +

−

=

−

− +

+

−

= η

η (13)

If we select the following update laws

su s

g g g

f f f

z Q w

z Q w

1 1

ˆ ˆ

−

−

=

=

&

&

(14)

then (12) becomes

2≤0

−

= s

V& η ₍₁₅₎

Hence s,w~_f,w~_g∈L_∞ . Square integrability of s is proved by

∫

∫

1

2dt Vdt (V V )

s η ^& η ^.

Boundedness of s^& can be easily justified from (11). Therefore, asymptotic convergence of s can be concluded by the Barbalat’s lemma. This further implies convergence of the output error e. Convergence of the parameters can be proved to depend on the PE condition of the reference input.

In the above derivation, we assume that a sufficient number of orthonormal functions are used and the approximation error is ignored. Here, let us consider the effect of the approximation error on the performance of the closed loop system. Instead of (10a) and (10b), f and g can be represented as

f f T

f =wfz +ε (16a)

g g T

g=wgz +ε (16b)

where ε_f ^and εg are approximation errors of f and g, respectively. Hence, the error dynamics (11) can be rewritten to be

ε

η + + +

−

= s u

s& w~^T_fz_f w~^T_gz_g (17)

where ε=ε(ε_f,ε_g,s,y^&&_d) is a lumped approximation error. If we still select (14) as the update laws, then the time derivative of V in (12) along the trajectory of (17) can be computed to be

ε ηs s

V&=− ²+ ₍₁₈₎

Due to the existence of ε, we may not determine definiteness of V&to conclude any stability property of the closed loop system. Let us proceed by representing (18) in the form V&≤(−ηs+ε)s .If we choose a proper η>0 and a suitable set of orthonormal functions, then V^&≤0 whenever











 >

∈ η

σ ε σ

s . This implies that the output error is bounded and the bound is a function of the approximation error.

In the rest of this section, we would like to consider the case when the bound of the approximation error is available, i.e., there exists a positive constant δ >0 such that ε ≤δ. This is a usual assumption in the neural network based control strategies (Ge et al. 1998). To cover the effect of this bounded approximation error, the controller (8) is modified to be

ˆ ) ˆ( 1

robust

d e s u

y g f

u= − +^&& −λ^&−η + ⁽¹⁹⁾

The robust term urobust is designed below. Let us consider the Lyapunov function candidate (12) again.

Its time derivative is computed as

robust

su s s

V^&≤−η ²+δ +

By selecting u_robust =−δsgn(s), we may have V&=−ηs²≤0, and asymptotic convergence of the output error can be further proved according to the Barbalat’s lemma.

4. SIMULATION AND EXPERIMENTAL RESULTS 4.1 Experiment setup

The proposed controller is implemented on an experimental system shown in Figure 2. The flexible arm is constructed from a 0.55 meter long and 0.6×45 mm section spring steel strip. The net weight of the strip is 0.128 kg, and the mass per unit length is 0.233 kg/m. The mass of the payload is 0.025 kg. With this design, the arm is very flexible in the horizontal plane. The actuator hub is directly coupled to a 90W DC servo motor driven by a PWM driver. The hub angle and angular velocity are obtained from a 1024-pulse encoder installed on the motor shaft. An HCTL-2020 chip is used to sample the encoder reading. A 12-bit D/A and two 8-bit A/D channels are used to interface with a 133MHz Pentium PC. Two strain gauges are employed to feedback system states. Strain gauge positions and their calibration can be found in Lin and Chu (1995). The proposed controller and update laws are implemented in a timer interrupt service routine under 10ms sampling rate.

4.2 Simulation results

Controller (8) is implemented with the update laws in (14) to control the given system. Initial condition for the simulation is x(0)=[−1 0 0]^T and we would like the end-point to track the trajectory y_d =0.55sint m⋅rad. The controller parameters are selected as λ=10 andη=10. Both f and g are approximated by the first 9 terms of the Fourier series, respectively. Initial weighting vectors are chosen as

T g

T f

] 0 0 20 [ ) 0 ˆ (

] 0 0 0 [ ) 0 ˆ (

L L

−

=

= w w

The first element in wˆ_g(0) is selected as a non-zero value to avoid singularity of gˆ(0). The adaptive gain matrices are selected as

9 ,..., 1 , 1 ),

,..., , (

9 ,..., 1 , 10 ),

,..., , (

9 2 1

9 2 1

3

=

∀

=

=

=

∀

=

= ⁻

i q q q q diag

i q

q q q diag

i i

g g g g g

f f f f f

Q Q

Although other values of

i

i g

f q

q and are also possible to have output error convergence as long as

g

f Q

Q and are positive definite, the above selection gives satisfactory performance. The simulation results are shown in Figure 3 to 6. Figure 3 shows that the end-point trajectory converges nicely to the

desired output. It is noted that the output y(x,t) defined in equation (1) is represented as the arc length; therefore, the unit of the vertical axis is m⋅rad. Figure 4 is the control torque in N⋅m. Its peak value is about 20 N⋅m in the transient. Figure 5 and 6 present the estimation performance of f and g, respectively. Since the output error converges within 0.5 seconds, there is no enough driving force for the update law to have parameter convergence, which can also be observed from (5) and (14). Although estimates of f and g do not converge to their true values, they remain bounded as proved in (15)

4.3 Experimental results

Same conditions are used in the real-time control on the actual flexible arm. The experimental results are shown in Figure 7 to 10. Figure 7 shows the output tracking performance. Figure 8 presents the voltage output of the D/A converter. Figure 9 and 10 show the boundedness of the estimates of f and g, respectively.

5. CONCLUSION

We have proposed an adaptive controller for a single-link flexible arm based on the function approximation technique. Analysis of the closed loop stability has been investigated with consideration of the approximation error. In implementing the controller, the control strategy does not need much knowledge about the system model as long as proper sets of basis functions are used. Both simulation and experimental results show that the proposed controller is able to give satisfactory tracking performance with only position and velocity feedback.

REFERENCES

[1] Bai, M., Zhou, D.H. and Schwarz, H., “Adaptive Augmented State Feedback control for an Experimental Planar Two-Link Flexible Manipulator,” IEEE Trans. on Robotics and Auto., Vol. 14, No.6, pp.940-950, 1998.

[2] Chen, X., Guo, S. and Fukuda, T. “Vibration Suppression Control of Flexible Arms by Using Sliding Mode Method” IEEE Int. Conf. on Control Appl., pp.309-314, 1999.

[3] Chen, X. and Fukuda, T. “Robust Sliding-Mode Tip Position Control for Flexible Arms” IEEE Trans. on Industrial Electronics, Vol. 48, pp.1048-1056, 2001.

[4] Cheong, J, Chung, W.K. and Youm, Y., “Fast Suppression of Vibration for Multi-Link Flexible Robots using Parameter Adaptive Control,” Proc. IEEE Int. Conf. on Intel. Rob. and Sys., pp.913-918, 2001

[5] Feliu, J.J., Feliu, V. and Cerrada, C., “Load Adaptive Control of Single-Link Flexible Arms Based on a New Modeling Technique,” IEEE Trans. on Robotics and Auto., Vol.15, No.5, pp.793-804, Oct. 1999.

[6] Ge, S.S., Lee, T.H. and Harris, C.J., Adaptive Neural Network Control of Robotic Manipulators, World Scientific Publishing, Singapore, 1998.

[7] Ge, S.S., Lee, T.H. and Wang, Z.P., “Adaptive Robust Controller Design for Multi-Link Flexible Robots,” Proc. of the American Control Conf., pp.947-952, 2001.

[8] Gokasan, M., bogosyan, O.S., Arabyan, A. and Sabanovic, A.,”A Sliding Mode Based Controller for a Flexible Arm with a Load,” Proc. Conf. of IEEE Industrial Electronics Society, pp.1083-1087, 1998.

[9] Gu, M. and Asokanthan, S.F., “Combined Discrete-Distributed Control of a Single-Link Flexible Manipulator Using a Lyapunov Approach,” ASME J. of Dyn. Sys., Meas. and Control, pp.448-456, Sept, 1999.

[10] Huang, A.C. and Kuo, Y.S., “Sliding Control of Nonlinear Systems Containing Time-varying Uncertainties with Unknown Bounds,” Int. J. of Control, Vol.74, No.3, pp.252-264, 2001.

[11] Huang, A.C. and Chen, Y.C., “Adaptive Multiple-Surface Sliding Control for Single-Link Flexible-Joint Robot with Mismatched Uncertainties,” accepted by IEEE Trans. on Control Sys.

Tech., 2002.

[12] Hisseine, D. and Lohmann, B. “Robust Control for Flexible-Link Manipulator Using Sliding Mode Techniques and Nonlinear H_∞ Control Design Methods”, IEEE Int. Conf. on Robotics and Auto., pp.3865-3870, 2001.

[13] Ioannou, P.A. and Sun, J. “Robust Adaptive Control”, Prentice Hall, 1996.

[14] Karandikar, D. and Bandyopadhyay, B. “Sliding Mode Control of Single Link Flexible Manipulator” Proc. of IEEE Int. Conf. on Industrial Tech., pp.712-717, 2000.

[15] Kwok, N.M. and Lee, C.K. “Control of a Flexible Manipulator Using a Sliding Mode Controller with a Fuzzy-Link Weighting Factor” IEEE Int. Symposium on Industrial Electronics, Vol.1, pp.52-57, 2001.

[16] Lin, Y.H. and Chu, C.L., “Numerical Evaluation for Stability and Performance of an Electronics Damping Device for Structural Vibration Control,” J. of Sound and Vibration, Vol.184, No.5, pp.929-933, 1995.

[17] Meirovitch, L. Analytical Methods in Vibrations, 1967.

[18] Narendra, K.S. Stable Adaptive System, Prentice-Hall, Inc., 1989.

[19] Queiroz, M.S., Dawson, D.M., Agarwal, M. and Zhang, F., “ Adaptive Nonlinear Boundary Control of a Flexible Link Robot Arm,” IEEE Trans. on Robotics and Auto., Vol.15, No.4, pp.779-787, Aug, 1999.

[20] Rhim, S. and Book, W.J., “Noise Effect on Adaptive Command Shaping Methods for Flexible Manipulator Control,” IEEE Trans. on Control Systems Technology, Vol. 9, No. 1, pp. 84-92, 2001.

[21] Rokui, M.R. and Khorasani, K, “Experimental Results on Discrete Time Nonlinear Adaptive Tracking Control of a Flexible-Link Manipulator,” IEEE Trans. on System, Man, and Cybernetics— Part B: Cybernetics, Vol. 30, No. 1, pp.151-164, 2000.

[22] Slotine, J-J. E. and Li, W. “Applied Nonlinear Control”, Englewood Cliffs, NJ: Prentice-Hall, 1991.

[23] Ryu, J.H., Kwon, D.S. and Park, Y. ”A Robust Controller Design Method for a Flexible Manipulator with a Time Varying Payload and Parameter Uncertainties”, IEEE Int. Conf. on Robotics and Auto., Vol.1, pp.413-418, 1999.

X Y

O X⁰

Y0

) θ(t

) , (xt ω

m

Figure 1 Single link flexible arm

Figure 2 Experimental setup

Signal processing circuit PWM driver HCTL 2020

A/D D/A car d

DC Servo Motor Encod er

Strain gages

Figure 3 Tracking performance (Simulation)

Figure 4 Control torque (Simulation)

Figure 5 Approximation of f (Simulation)

Figure 6 Approximation of g (Simulation)

Figure 7 Tracking performance (Experiment)

Figure 8 Control voltage (Experiment)

Figure 9 Approximation of f (Experiment)

Figure 10 Approximation of g (Experiment)