Fast Algorithm for Robust Template Matching with M-estimators

Fast Algorithm for Robust Template Matching with M-estimators

Jiun-Hung Chen, Chu-Song Chen, and Yong-Sheng Chen Institute of Information Science, Academia Sinica, Taipei, Taiwan

e-mail: song@iis.sinica.edu.tw

Abstract

In this paper, we propose a fast algorithm for speeding up the process of template matching that uses M-estimators for dealing with outliers. We propose a particular image hierarchy called the p-pyramid that can be exploited to generate a list of ascending lower bounds of the minimal matching errors when a non-decreasing robust error measure is adopted. Then, the set of lower bounds can be used to prune the search of the p-pyramid, and a fast algorithm is thereby developed in this paper.

This fast algorithm ensures finding the global minimum of the robust template matching problem in which a non-decreasing M-estimator serves as an error measure. Experimental results demonstrate the effectiveness of our method.

Index Terms —Template matching, robust template matching, M-estimator, fast algorithm.

I. Introduction

Finding a pattern or template in a signal is an important problem for signal and image processing.

This so-called template matching can be applied to many applications such as image and video coding, pattern recognition, and visual tracking. It is usually assumed in template matching that the signal segments of interests do not change their appearances very much. Hence, template matching based on the criteria such as the sum of absolute difference (SAD) or the sum of squared difference (SSD) is commonly adopted. The popularity of using template matching for applications of signal or image processing is mainly due to its ease of implementation together with the many fast algorithms that can be used to speed up the matching process for various applications [1,7-8,13,15,22,25-26,28-29,35,39].

In a cluttered environment, however, some outliers such as impulse noises or partial occlusions may occur during the matching processes. In this situation, the SAD and SSD criteria are no longer suitable for template matching because they treat the outliers and inliers evenly when calculating the

error measures. One possible remedy for this weakness is to use a robust criterion instead of SAD or SSD. For this, the M-estimator technique [2][16][30][38] is one of the most popular methods to solve the problem of robust parameter estimation, and has been applied in many studies [3-5,11-12,14,23,31-33,36]. The basic idea of the M-estimator technique is to limit the influence of outliers in the matching error. In principle, the effects of the outlier can be suppressed with the M-estimator technique and therefore better estimations are obtained.

A typical procedure for finding solutions with M-estimators is the iterative-reweight procedure [30].

In each iteration of this procedure, a weighted least-square problem is solved and then the weights are adjusted for the next iteration for further refinement. Hence, when applying the iterative-reweight procedure for robust template matching, in each iteration, another template matching problem must be solved based on a weighted SSD error measure, in addition to which, multiple iterations are also necessary. Therefore, the computation of robust error measures is very time-consuming, although more accurate results can be obtained by adopting a robust error measure instead of non-robust ones.

1 In the past, many methods have been proposed to speed up the matching process where the simple SAD or SSD criterion is used. However, to our knowledge, no method has been addressed for speeding up the process of template matching where robust error measures are used. In this paper, we propose a fast method for solving this problem. We will present this method by assuming that a 2D signal (e.g., an image) is used. Nevertheless, our algorithm can be easily generalized for any d-dimensional signal, d∈ N⁺.

On the other hand, there are already many methods for speeding up the process of template matching where non-robust error measures are used. These methods can be divided into two classes. The methods in the first class only find a local minimum while the ones in the second class definitely find the global minimum. In principle, almost all the methods in the first class formulate the template matching as a search problem and find a solution by adopting the greedy strategy. Examples include the three-step search algorithm [22], the gradient-descent based method [29] and others [1][8][13][15]

[28][35][39]. The genetic algorithm-based methods [8][28] or the simulated annealing-based method [35] may have chances of finding the global minimum if their parameters are set appropriately to the given problems, but can not ensure that it will always be found. In essence, since these methods do not guarantee finding the global minimum, they are generally faster than those ensuring the global optimality.

The methods in the second class guarantee finding the global minimum, and the main idea of this class is basically prune and search [26][25][7]. Hence, the main issue of this class of approaches is on how to design the search strategies for pruning unnecessary searching branches. The successive elimination algorithm proposed by Li and Salari [26] eliminates impossible sites successively during

the searching process by using lower bounds derived from the triangle inequality. Their method can guarantee obtaining the global minimum, as does the full search (FS) method, and it is more efficient.

In [25], Lee and Chen extended this idea by using a block-sum-pyramid structure, where a set of ascending lower bounds can be derived and serve as useful guidelines to prune the search process.

However, the performance of their method depends on the search order. Recently, Chen et al.

further refined it by using a winner-update strategy [7], which is not only irrelevant to the search order but is also faster.

Similar to those methods that ensure finding the global minimum but using non-robust error measures introduced above [26][25][7], the method developed in this paper also adopts an inequality in a particular image hierarchy to speed up the template-matching process with robust error measures. In essence, a set of ascending lower bounds of the minimal matching error can be generated with our method as long as the robust error measure is non-decreasing. This set of lower bounds can then serve as useful guidelines for pruning the redundant branches of the searching process. In addition, our method can ensure finding the global minimum, as the FS method does for robust template matching.

This paper is organized as follows. Section II introduces the image hierarchy used in this work and the associated ascending lower bound list. Section III presents the search strategies and our main algorithm. Section IV shows some experimental results. Finally, some discussion and conclusions are given in Sections V and VI, respectively.

II. Problem Formulation, P-pyramid, and Fundamental Inequality

A. Problem Formulation

We denote I(i,j) as the intensity at position (i,j) in an image I. Assume that I1 and I2 are N×N images.

The sum of robust differences (SRD) between two images I1 and I2 is defined as follows:

( ) ∑ ( ( ) ( ) )

−

≤

≤

−

≡

1 , 0

2 1

2 1

, , , , ,

N j i

j i I j i I I

I

SRD_ρσ ρ σ (1)

where ρ(⋅,⋅) : R⁺∪{0} × R⁺ → R⁺∪{0} is a robust error measure (or a robust loss function) [2][16][38] and σ is a parameter controlling the shape of ρ(⋅,⋅). ² Typically, the robust error measure, ρ(⋅,⋅), is selected according to how it reduces the influences of outliers. Given an image template It

whose size is N ×N and an image F whose size is (2W+N) × (2W+N), the robust template matching

1 Another problem of the iterative-reweight procedure is that it can not definitely find the global optimum.

2 Some common robust error measures will be introduced in Section II. E. In particular, if ρ(x,σ) = x² (or x) for all σ, then (1) becomes SSD (or SAD).

problem is defined as finding the position (u*, v*) with the minimum SRD among all possible search positions in the image F.

( ) ( )

( ) ( )

( )

∑

≤ −

≤ ≤

≤

≤

≤

+ +

−

=

≡

1 , , 0

, , ,

*

*

, , ,

, ,

N j i W t v u -W

v u W t

v u -W

v j u i F j i I min

arg

F I SRD min arg v

u

σ ρ

σ ρ

(2)

where Fu,v is an N ×N image block with its upper-left point being (u,v) in the image F and the number of search sites is (2W+1) × (2W+1).

B. P-feasible

To simplify the notation of the robust error measures, we define

τ_σ(x) = ρ(x,σ) for all x∈R⁺∪{0}, (3)

and abbreviate τ_σ(x) to be τ(x) for the cases without ambiguity in the following.

Definition 1 [p-feasible]: A robust error measure τ(⋅) is p-feasible if it satisfies both the following two conditions:

(1) τ(⋅) is non-decreasing, i.e., a1≥a2 implies τ(a1) ≥ τ(a2) for all a1, a2∈R⁺∪{0}, and

(2) for each pair of nonnegative values (a1,a2), the following inequality with respect to the Lp-norm holds:

∀a1, a2 ∈ R⁺∪{0}, τ(a1) + τ(a2) ≥ τ(||a||p) (4) where a=[a1 a2]^T is a 2-D vector and ||a||p=(|a1|^p+|a2|^p)^1/p is the Lp-norm of a, p∈[1 ∞]. In particular,

||a||∞=max(|a1|,|a2|).

Some properties associated with the p-feasible defined above are investigated below:

Property 1: Every non-decreasing τ(⋅) is ∞-feasible.

pf: This property can be easily derived according to the definitions.

Property 2: If a robust error measure τ(⋅) is p-feasible, that implies it is also q-feasible for all q∈[p

∞].

pf: See Appendix A.

If a p-feasible robust error measure is used as the matching criterion, an ascending lower bound list of the matching errors can be obtained by constructing an image pyramid with respect to the Lp-norm, as described in the following.

C. P-pyramid and Fundamental Inequality

Assume that N = 2ⁿ (n∈N⁺). For each N ×N image block I = Fu,v (-W

≤

u,v

≤

W) that is contained in the image F, a p-pyramid of I is defined as a set of images {I^0,p,⋅⋅⋅,I^m-1,p,I^m,p,⋅⋅⋅, I^n,p}, where I^n,p = I and the size of I^m,p is 2^m×2^m (0

≤

m

≤

n, m

∈

N⁺∪{0}). I^m,p is referred to as the image on the level m of the p-pyramid. Level 0 and level n are called the highest and the lowest levels of the p-pyramid, respectively. Given an image I^m,p on the level m, the image I^m-1,p on the level m-1 is constructed using the following equation:

( )

p

p m

j i p

m i j

I ^−1, , = I_,^, (5) where

( ) ( ) ( ) ( )

[

^{mp mp mp mp}

]

^T

p m

j

i_,^, = I ^, 2i,2j I ^, 2i,2j+1 I ^, 2i+1,2j I ^, 2i+1,2j+1

I and 0≤i,j≤2^m-1−1.

Accordingly, the pyramids from level n to level 0 can be constructed iteratively. Totally, (2W+1)×

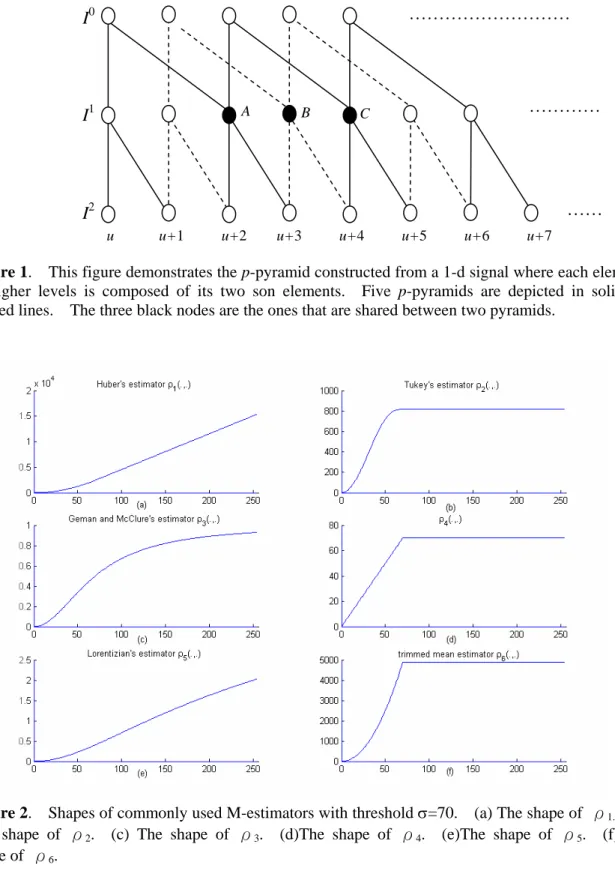
(2W+1) p-pyramids are constructed from the image F. Figure 1 shows an illustration of the pyramids constructed from a 1-D signal.

Following the notions shown in (1), we define the SRD between I1 and I2 on the level m by

( ) (

^{mp mp}

)

p

m I I SRD I I

SRD_ρ,^,_{σ 1}, ₂ = _{ρ,σ 1}^, , ₂^, for m = 0, 1, ⋅⋅⋅, n. Furthermore, we denote SRD_τ(I1,I2) = SRDρ,σ(I1,I2) if a fixed σ is considered (where τ(⋅) is defined in (3)). Then, it can be shown that the following fundamental inequality holds for the image hierarchy defined above.

Theorem 1: Given a robust error measure τ(⋅) that is p-feasible, then for all I1, I2,

(

I^np I^np

)

SRD

(

I^{n p} I^{n p}

)

SRD

(

I ^p I ^p

)

SRD_{τ 1}^, , ₂^, ≥ _{τ 1}^−1, , ₂^−1, ≥L≥ _{τ 1}^0, , ₂^0, (6)

pf: See Appendix B.

Hence, given a image template It and an image block Fu,v (-W ≤ u,v ≤ W), a set of ascending lower bounds, SRD_τ^m,p

(

F_u,v,I_t

)

, m=0, 1,⋅⋅⋅, n can be obtained according to Theorem 1.

Notice that the number of robust differences involved in the computation of each lower bound

(

u,v t

)

p ,

m F ,I

SRD_τ (0≤m<n) is 2^m×2^m, which is smaller than 2ⁿ×2ⁿ, the number of robust differences required for

(

uv t

)

p

n F I

SRD_τ^, _, , . Therefore, the lower bounds can be computed more efficiently than the sum of robust differences with respect to the original image. In particular, the higher are the levels in a pyramid, the faster are the computations of the associated lower bounds. In fact, the ratio

of the required number of the computations of the robust differences on the level m to that required for the level n is

n−m

4

1 . Accordingly, even when all of the lower bounds are computed, the required

time is less than

∑

⁻

=¹ − ≤

1 3

1 4

n 1

m n m of that required for the level n, the original image block. Such an ascending lower bound list of the matching error can be used for speeding up the matching process by incorporating it into a systematic search strategy, as introduced in Section III.

Remark 1 [Efficient Construction of the P-pyramids of an Image]: A p-pyramid of each image block can be constructed independently by using (5). However, it is very time-consuming if each pyramid is constructed independently. In fact, the p-pyramids can be constructed more efficiently by considering the computation and storage redundancies between neighboring image blocks when constructing and storing the p-pyramids. We introduce this method by using an example, as shown in Figure 1. Considering node A in the first level image of Pyramid 1, as shown in Figure 1, one can observe that node A is also contained in Pyramid 3. Similarly, node B (or C) is shared by Pyramids 2 and 4 (or Pyramids 3 and 5). Hence, if each pyramid is constructed independently according to (5), the values of nodes A, B, and C will be computed twice, once for each pyramid. In our work, to remove this redundancy and to save computation and storage of the p-pyramids for all the image blocks, the method illustrated in Figure 1 is adopted. That is, I¹, the image containing every node of the first-level images of all the pyramids, is first constructed based on I². Similarly, I⁰ can be constructed based on I¹. After I⁰ and I¹ are constructed, all the pyramids are then available, as shown in Figure 1. More details about efficient construction of pyramids can be found in [7].

Remark 2 [Free Sampling]: In the above description, a particular level of the p-pyramid is built with the Lp-norm of the 2×2 points from its lower neighbor level, as shown in (5). We refer to it as the 2-2 down-sampling in this case. In general, we can use m-n down-sampling instead of 2-2 down-sampling for all m, n∈N⁺, and the associated p-pyramid can be reconstructed in a similar way as well. Similarly, m down-sampling can be used for a 1-D signal and m-n-k down-sampling can be used for a 3-D signal, and so on, where k∈N⁺.

D. Characterization of P-feasible Robust Error Measures

In Section II.C, we have shown that if a p-feasible robust error measure is selected for template matching, then we can construct an ascending lower bound list associated with a particular image hierarchy, the p-pyramid. Before introducing the search procedure that exploits the series of lower bounds in detail, we illustrate an important issue about whether such a lower-bound list can be constructed. In particular, the following problem is worthy to be addressed:

“Given a robust error measure τ(⋅), under what condition can it be ensured that we can always

find a p∈[1 ∞] such that τ(⋅) is p-feasible?”

In this paper, we tackle this problem in consideration of the class of non-decreasing robust error measures. In fact, Property 1 has shown that if a robust error measure is non-decreasing, it is

∞-feasible. Therefore, when the ∞-pyramids are built for both the template and the image blocks, an ascending lower bound list can then be constructed according to Theorem 1. Hence, it ensures that every non-decreasing robust error measure is p-feasible for some p because p=∞ is a trivial solution.

3 In addition to p=∞, let us further investigate the other p values that allow a robust error measure to be p-feasible. Given a non-decreasing robust error measure, τ(⋅), let Γ_τ, the feasible set associated with τ, be defined as the set of values allowing τ(⋅) to be p-feasible: Γτ = {p∈[1 ∞] | τ is p-feasible}.

By considering the maximal lower bound of Γτ, the following property can be derived:

Property 3: Given a τ(⋅) that is non-decreasing, there exists a discriminative value p’ such that τ(⋅) is p-feasible for all p∈(p' ∞] and is not p-feasible for all p∈[1 p'), where p’ is the maximal lower bound of Γτ, the feasible set associated with τ.

pf: This property can be derived directly from Properties 1 and 2.

Hence, the feasible set associated with a robust error measure can be clearly specified with its discriminative value p’ by further identifying the following two conditions: τ is p’-feasible or τ is not p’-feasible. If τ is p’-feasible, then Γτ = [p' ∞]; otherwise, Γτ = (p' ∞]. After specifying the feasible set, another problem worth consideration is

“Which p contained in the feasible set associated with a non-decreasing robust error measure is a better choice for speeding up the process of robust template matching?”

We investigate the above problem from the implementation point of view. In practice, to simplify the computation, it is better to select p as integers instead of floating-point numbers. When p is restricted to being an integer, the feasible set associated with τ(⋅) can then be uniquely specified by Γ_τ

= {n∈N⁺∪{∞} | n≥n’, n’∈N⁺∪{∞}}, where n’=

⎡ ⎤

p′ . In particular, we call τ(⋅) to be minimal n’-feasible in this case, and n’ is also referred to as the minimal feasible value of τ(⋅). Note that the smaller is n, the less is the computational overhead of the Ln-norm for n∈N⁺. Therefore, a better choice of n is therefore n=n’. ⁴

3 How to construct a list of ascending lower bounds for the general class of robust error measures that are not necessary to be non-decreasing remains an open problem.

4 Although the computation of the ∞-norm is also simple since only the absolute values and the max(⋅,⋅) operations are involved, we find that in practice its speedup performance is usually worse because the lower bounds associated with an

∞-pyramid are usually not tight enough. An example is given in Section IV. A.

E. Minimal Feasible Value of Commonly Used Robust Error Measures

In the following, we will give a study of the minimal feasible values for some commonly used robust error measures. An interesting phenomenon shown below is that almost all commonly used non-decreasing robust error measures are minimal 1-feasible or minimal 2-feasible.

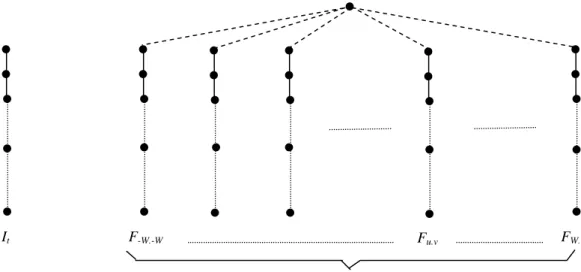
Given a robust error measure ρ(⋅,⋅), we define H_ρ={ρ(⋅,σ)|σ∈R⁺}. The Huber's estimator ρ1(⋅,⋅) (see Figure 2(a)) has least squares behaviors for small residues, and the more robust least-absolute-values behavior for large residues [14][19][31][33]:

( )

⎪⎪

⎩

⎪⎪⎨

⎧

⎟⎠

⎜ ⎞

⎝⎛ −

≤

=

otherwise.

2

, if 2 ,

2

1 σ σ

σ σ ρ

r r r

r (7)

Property 4: Each member of Huber’s estimators,

ρ1

H , is minimal 2-feasible.

pf: See Appendix C.

The Tukey's estimator ρ2(⋅,⋅) (see Figure 2(b)) has zero weights ⁵ for the large residues and thus improves the outlier rejection properties [4][5][11][14][19][31].

( )

⎪⎪

⎩

⎪⎪

⎨

⎧

⎥ ≤

⎥

⎦

⎤

⎢⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛ ⎟

⎠

⎜ ⎞

⎝

⎛

=

otherwise.

6

, if - r

1 - 6 1 ,

2

2 3 2

2 σ

σ σ σ

σ

ρ r ^r (8)

The shape of the function ρ2(⋅,⋅) is shown in Figure 2(b).

Property 5: Each member of Tukey’s estimators,

ρ2

H , is minimal 2-feasible.

pf: See [6].

Another popular class of the robust error measure is the one proposed by Geman and McClure [12]

(see Figure 2(c)) as shown below, which was also adopted in [3][4][23][31].

( )

₂ ² ₂

3 ,

σ σ

ρ = +

r

r r (9)

5 In robust statistics, the weight is defined to be an value proportional to the derivatives ofρ.

Property 6: Each member of Geman and McClures’ estimators,

ρ3

H , is minimal 2-feasible.

pf: See [6].

The above three robust error measures are popular, and we have shown that all members of their Hρs have the minimal feasible value as 2. In addition, the following three robust error measures are also investigated.

The robust function ρ4(⋅,⋅) [36] (see Figure 2(d)) uses simple truncations to remove outliers, as shown in the following:

( )

⎩⎨⎧ ≤

= otherwise.

, if

4 , σ

σ σ

ρ r ^{r r} (10)

Another two robust error measures investigated here are Lorentizian's estimator ρ5(⋅,⋅) [19] (see Figure 2(e)) and the trimmed mean M-estimator ρ6(⋅,⋅) [31] (see Figure 2(f)):

( )

_⎟^⎟

⎠

⎞

⎜⎜

⎝

⎛ ⎟

⎠

⎜ ⎞

⎝ + ⎛

=

2

5 2

1 1

,σ σ

ρ r log ^r (11)

( )

⎪⎪

⎩

⎪⎪⎨

⎧ ≤

=

otherwise.

2

, if

, 2₂

2

6 σ

σ σ

ρ ^r

r

r (12)

Property 7: (i) Each member of

ρ4

H is minimal 1-feasible. (ii) Each member of

ρ5

H is minimal 2-feasible. (iii) Each member of

ρ6

H is minimal 2-feasible.

pf: See [6].

Notice that all the minimal feasible values of the commonly used non-decreasing robust error measures investigated above are 1 or 2, which are indeed small values.

In the following, we investigate an M-estimator that is not non-decreasing, the triweight M-estimator ρ7(⋅,⋅) [32]:

( )

⎪

⎩

⎪⎨

⎧

≤

<

≤

=

otherwise.

0

, 3 if

, if

, ²

2

7 σ σ σ

σ σ

ρ r

r r

r (13)

Since each member of

ρ7

H is not non-decreasing, the process of template matching can not be speeded up with our approach if ρ7 is selected to be the robust error measure.

Finally, we investigate the non-decreasing error measure shown as follows, where k∈N⁺.

ρ₈

( )

r,σ =r^k, (14) Property 8: Each member of

ρ8

H is minimal k-feasible.

pf: Trivial.

When k=1 (or k=2), ρ8 becomes the SAD (or SSD) error measure. The SAD and SSD are therefore minimal 1-feasible and minimal 2-feasible, respectively. Hence, our method can also be used to speed up the template matching process where SAD or SSD is used as the error measure.

III. Search Strategy and The Main Algorithm

A. Search Strategy

Once an ascending lower bound list of the matching error is available for every search position (u,v), many search strategies [26][25][7] can be used to speed up the process of robust template matching in our work. A brief review of these search strategies is given below. Without loss of generality, the p-pyramid serves as the pyramidal structure for describing these methods. We refer to p-pyramid as pyramid in the following. Consider a template It and a set of image blocks Fu,v (-W

≤

u,v

≤

W) to be matched, where It and Fu,v are both N×N images. Assume that the associated p-pyramids have been constructed for It and all of the Fu,v, -W

≤

u,v

≤

W, respectively.

In [26], only the highest level and the lowest level of the pyramids were used. The search order of the matching process is fixed and, without loss of generality, assume that the matching process starts from F-W,-W and the search is performed in a row-major order. First, the error SRDτ(F-W,-W, It) is computed as a reference value, r. Then, assume that (u',v') is the next site to be visited in the matching order. We try to find out whether the robust error measure SRDτ(Fu′,v′ , It) is smaller than r.

We do not compute SRDτ(Fu',v' , It) directly. Instead, we first compute

(

uv t

)

p F I

SRD_τ^0, _′,′, , the error associated with the highest levels of the pyramids of It and Fu',v'. If

(

uv t

)

p F I

SRD_τ^0, _′,′, is larger than the current reference value r, we do not have to further compute SRDτ(Fu',v', It) because

(

u v t

)

p

0 F I

SRD_τ^, _',', is a lower bound of SRD_τ(Fu',v', It). Therefore, early in the process we can jump out of the process of matching It and Fu',v' and go on to match the next image block in the row-major

order. On the other hand, if

(

uv t

)

p F I

SRD_τ^0, _′,′, is smaller than the current reference value r, we must compute SRDτ(Fu',v', It) and compare it with r. If SRDτ(Fu',v', It) is smaller than r, the current reference value, then r is replaced by SRD_τ(Fu',v', It). The above procedure can be repeated iteratively.

Remember that the computation complexity of

(

u v t

)

p

0 F I

SRD_τ^, _',', is 4n

1 of that required for

SRDτ(Fu',v', It), and thus such an early jump-out effect saves considerable computation time.

Lee and Chen [25] extended the idea of [26], using not only the highest and the lowest levels, but all the levels of the pyramids. First, the error SRDτ(F-W,-W, It) is also computed as a reference value, r.

Then, once we begin to match It and Fu',v' for some (u',v') depicted above, not only is

(

uv t

)

p F I

SRD_τ^0, _′,′, computed, but a set of increasingly larger lower bounds,

(

uv t

)

p F I

SRD_τ^0, _′,′, ,

(

uv t

)

p F I

SRD_τ^1, _′,′, ,

(

_{u v t}

)

p F I

SRD_τ^2, _′,′, , ..., are also computed in turn if necessary. Once some SRD_τ^i,p

(

F_u′,v′,I_t

)

(i = 0, 1, ..., n) is larger than the current reference value r, we have no need to compute all the other

(

u v t

)

p

j F I

SRD_τ^, _′,′, for j = i+1, ..., n, and the matching process between It and Fu',v' can be terminated.

We can then jump to another matching process between It and the next image block of Fu',v' in the row-major order. This method can be treated as using a depth-first search procedure in visiting the search tree as shown in Figure 3, and pruning the search branches once the computed error associated with the tree vertex is larger than the current reference value.

Recently, Chen et al. [7] extended the above method by exploiting the uniform cost search [34] in the tree instead of the depth-first search, so that the search order is not fixed. First, the smallest value among all the errors of the highest level is found:

(

_{u v t}

)

p F I

SRD_τ^0, _*,*, = min(the elements of A), where A = {

(

W W t

)

p F I

SRD_τ^0, _{− ,−} , ,

(

W W t

)

p F I

SRD_τ^0, _{− ,− +1}, , ...,

(

WW t

)

p F I

SRD_τ^0, _, , } is referred to as the active list, and (u*,v*) is referred to as the temporary winner. Then, the error of the temporary winner in its next lower layer, SRD_τ^1,p

(

F_u*,v*,I_t

)

, is computed. Next, the active list is updated by replacing

(

u v t

)

p F I

SRD_τ^0, _*,*, with

(

u v t

)

p F I

SRD_τ^1, _*,*, : A ← A ∪ {

(

u v t

)

p F I

SRD_τ^1, _*,*, } \ {

(

u v t

)

p F I

SRD_τ^0, _*,*, }, where “\” is the set difference.

Then, the new minimal value among the elements in the new active list can be found:

(

u v t

)

p

i F I

SRD^, _{*, *},

1

τ 1 = min(the elements of A)

where i is now either 0 or 1, and a new temporary winner, (u*,v*) is obtained. Repeat the above procedure of alternately updating the active list and finding the minimal value of the elements

contained in it. Then, the minimal matching error can be found when (u*,v*) reaches the lowest level. In general, this method can prune more unnecessary branches because the uniform cost search strategy is used.

Once the p-pyramids have been constructed for the template and image blocks using the method introduced in this paper, it can be incorporated into any of the search strategies introduced above in order to speed up the process of robust template matching. In this work, the search strategy developed in [7] is adopted because the experimental results in [7] show that better speedup performance can be obtained compared with other approaches for non-robust template matching.

B. Main Algorithm

The algorithm of our approach using the uniform cost search for fast robust template matching is given below:

Step 1. Initially, set A = {

(

W W t

)

p F I

SRD_τ^0, _{− ,−} , ,

(

W W t

)

p F I

SRD_τ^0, _{− ,− +1}, , ...,

(

WW t

)

p F I

SRD_τ^0, _, , }.

Step 2. Find (u*, v*) such that

(

u v t

)

p F I

SRD_τ^0, _*,*, is the minimum among all the elements contained in A.

Step 3. i ← 0.

Step 4. While (i≠n)

4.1. Compute

(

u v t

)

p

i F I

SRD_τ^+1, _*,*, .

4.2. A ← A ∪ {SRD_τ^i+1,p

(

F_u*,v*,I_t

)

} \ {SRD_τ^i,p

(

F_u*,v*,I_t

)

} 4.3. Find (u*, v*, j) such that

(

u v t

)

p

j F I

SRD_τ^, _*,*, is the minimum among all the elements contained in A.

4.4. i ← j.

end While

Step 5. Output (u*, v*).

The above algorithm applies the “uniform cost search” [34] to the tree illustrated in Figure 3, which guarantees to find the global minimum solution as demonstrated in the following. When the algorithm goes to step 5, we know that

(

u v t

)

p

n F I

SRD_τ^, _*,*, is the minimum among all the elements contained in A. In addition, from Theorem 1, the matching error computed for any two images on the level n is not smaller than that for the other levels. Assume that A = {

(

W W t

)

p

n F I

SRD_τ^−W,−W, _{− ,−} , ,

(

W W t

)

p

n F I

SRD_τ^−W,−W+1, _{− ,− +1}, , …,

(

WW t

)

p

n F I

SRD_τ^W,W, _, , }. Then,

(

ij t

)

p

n F I

SRD_τ^, _, , ≥

(

ij t

)

p

n F I

SRD_τ^i,j, _, , ≥

(

u v t

)

p

n F I

SRD_τ^, _*,*, for all

(

ij t

)

p

n F I

SRD_τ^i,j, _, , ∈ A, or equivalently, for all –W≤i,j≤W, which shows that

(

u v t

)

p

n F I

SRD_τ^, _*,*, is the global minimal on the level n.

In fact, instead of from the highest to the lowest levels (i.e., from level 0 to level n), the search process can also be performed from an arbitrary middle level, say m (0<m<n), to the lowest level, n. This can simply be achieved by replacing each SRD_τ^0,p with SRD_τ^m,p in the Steps 1 and 2 of the main algorithm, and further modifying Step 3 to be i = m. However, in our experience, it is better to select the starting level based on the ratio of outliers. In particular, we find that starting from a middle level (instead of the highest level) usually makes the process of robust template matching more efficient in practice. This is because the outliers contained in the template are included in the highest level image, although they may not be included in some middle level images. Some experimental results for the speedup versus different combinations of the starting levels and outlier ratios are shown in Section IV.

In practice, some standard methods [30][38][40] can be used to estimate an appropriate value for the parameter σ in robust estimation. For example, the “median absolute deviation” scale estimate, which is related to the median of the absolute values of the residuals, is given by

i ri

median p

n

⎥⎦ ⎤

⎢⎣ ⎡ + −

= 1 . 4826 1 5 ( )

σ ˆ

, (15)

where the constant 1.4826 is a finite sample correction factor, n is the size of the data set, p is the dimension of the parameter vector, and r_i is the residual error.

IV. Experimental Results

In this section, we present the results of three different experiments, including signal matching, face template matching, and motion estimation.

A. Signal Matching

In this experiment, we perform a simulation of searching a particular 1-D pattern along a 8192-point input signal, ranging from 0 to 255, which is synthesized using a linear regression model. Four such input signals are used for this experiment, and one of them is shown in Figure 4(a). We first randomly extract a 512-point partial segment, which is called the true identity signal, from an input signal. A 512-point test signal can then be generated by adding both Gaussian noise and some outliers to the true identity signal, as shown in Figures 4(b), 4(c), and 4(d), respectively. The outlier ratio (i.e., the ratio of the number of outlier points to the length of a test signal, 512) varies from 0 to 0.15. Then the test signal is used as a template and we try to find its matching segment in the input

signal from which the test signal is extracted. In fact, this experiment simulates stereo matching (i.e., matching along a scan-line or epi-polar line) in computer vision [20]. Here, the SRD is used as the matching criterion. For each input signal and each outlier ratio, we first randomly generate 30 test signals and then find their matching segment in the input signal. The simple-truncation function (10) is used in this experiment as a robust error measure to suppress the effects of outliers. If the matching segment is not equal to its true identity signal, a miss occurs. Otherwise, a hit occurs. In this experiment, high average hit ratios ranging from 99.7% to 99.8% are achieved for all outlier ratios tested, which indicates that the M-estimator is very useful for suppressing the outlier effects.

In the following, we focus on the main issue of this paper, the speedup of robust template matching, by comparing the efficiencies of our method with respect to those of the FS method.

First, we investigate the advantage of our method for the reduction of the major operations involved in the SRD computations. We define a robust operation to be the computation of the robust error measure ρ(⋅,⋅), and computing ρ(⋅,⋅) n times is therefore referred to as that n robust operations are performed. The robust operation is generally the most critical part for obtaining an SRD. The efficiency improvement with our method is evaluated by comparing the following two ratios: (1) the ratio of robust operations involved in our method to that in the FS method, and (2) the ratio of the execution time with our method to that with the FS method. These two ratios are referred to as the operation count ratio and the time consumption ratio, respectively. Evaluation of the efficiency improvement based on the operation count ratios is machine independent, but some additional computational overheads such as the construction of the p-pyramids and the switching among the search braches can not be reflected by the operation count ratios. On the other hand, evaluation based on the time consumption ratios includes all the overheads, but is machine dependent. In this experiment, both the operation count ratios and time consumption ratios are computed for evaluations and comparisons. In the setting of this experiment, there are a total of 10 levels (level 0 to level 9) in the pyramid because the length of the test signal, 512, is equal to 2⁹. Remember that our algorithm can start from any of the middle levels, as described in Section IV. Therefore, we also compare the speedup effect when the matching processes start from different initial levels in this experiment.

Since the simple truncation function is minimal 1-feasible, the 1-pyramid is constructed for robust template matching with our method. The operation count ratios using 1-pyramid are shown in Figure 5(a). From Figure 5(a), the operation count ratio varies overall from 0.1 to 0.48 when the outlier ratio varies from 0 to 0.15, if the middle value of the operation count ratios serves as a representative for each outlier ratio. This shows that our method can successively reduce the number of the major operations required for robust template matching, and the smaller the outlier ratio, the more reductions are achieved. An interesting phenomenon is that the best starting level (i.e., the starting level associated with the smallest operation count ratio) for each outlier ratio is a middle level.

For example, when the outlier ratio lies in [0 0.02], the best starting level is 5; whereas when the outlier ratios are increased to be within [0.04 0.08] and [0 .1 0.15], the associated best starting levels become 6 and 7, respectively. The reason for this is that the outliers are easily to be included in the accumulation process for building a high level image in the pyramid, and thus almost all the lower bounds with respect to a high level image are required to be computed in the search process. On the other hand, when starting from a low level image, the lower bounds may not be tight enough to prune the search branches. Another interesting phenomenon is that the best starting level becomes lower as the outlier ratio increases.

Figure 5(b) shows the time-consumption ratios taking into account not only the major operations but all the computational overheads such as pyramid constructions and controlling processes of search.

The test was performed on a PC with the Visual C++ language, and the middle levels, 5, 6, 7, and 8 were used as the starting levels, respectively. From Figure 5(b), the time consumption ratio varies overall from 0.4 to 0.6 when the outlier ratio varies from 0 to 0.15, indicating that our method can also increase the efficiency of robust template matching in practice. Similarly, the best starting level becomes lower when the outlier ratio increases, and the best time consumption ratio varies from 0.2 to 0.4. Hence, if priori knowledge about the outlier ratio of the template matching problem to be solved is given in advance, this can serve as a guideline to choose the best (or a better) starting level.

Notice that the simple truncation is minimal 1-feasible, and it is therefore also p-feasible for all p∈[1

∞]. In the following, different p-pyramids (1-pyramid, 2-pyramid, and ∞-pyramid) are respectively constructed to compare their efficiencies when they are incorporated into our method. Their average operation count and time consumption ratios are summarized in Table 1, showing that the speedup performance degrades when either the 2-pyramid or the ∞-pyramid is used. This matches our claim above that the closer is p to its minimal feasible value, the better speedup is achieved when the p-pyramid is used.

A summary of the above experimental results is given below. First, the hit ratio is high when the technique of robust template matching is used, confirming that the SRD can suppress the affection of outliers. Second, from both the operation count and the time consumption ratios, our method is more efficient than the FS method. The amount of speedup achieved depends on many issues such as outlier ratios, starting levels, and the p-pyramid being used. In practice, the starting level should be selected according to the outlier ratio. If an estimation of the outlier is available in advance, the best starting level can be chosen according to the corresponding simulation results. As for which p-pyramid is suitable to be adopted in our method for a given robust error measure, it is suggested that the closer is p to its minimal feasible value, the more speedup is achieved.

Table 1.

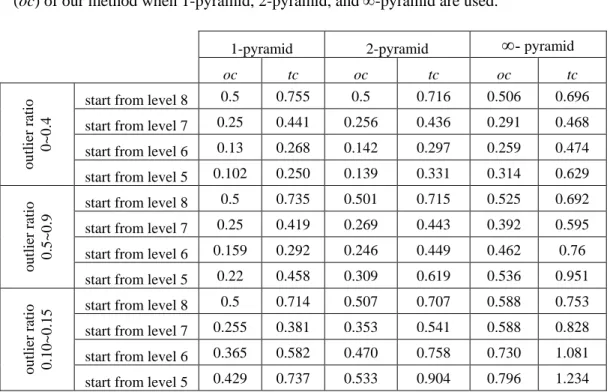
Comparisons of average time consumption ratio (tc) and average operation count ratios (oc) of our method when 1-pyramid, 2-pyramid, and ∞-pyramid are used.

1-pyramid 2-pyramid

∞-

pyramid

oc tc oc tc oc tc

start from level 8 0.5 0.755 0.5 0.716 0.506 0.696

start from level 7 0.25 0.441 0.256 0.436 0.291 0.468 start from level 6 0.13 0.268 0.142 0.297 0.259 0.474 outlier ratio 0~0.4

start from level 5 0.102 0.250 0.139 0.331 0.314 0.629 start from level 8 0.5 0.735 0.501 0.715 0.525 0.692 start from level 7 0.25 0.419 0.269 0.443 0.392 0.595 start from level 6 0.159 0.292 0.246 0.449 0.462 0.76 outlier ratio 0.5~0.9

start from level 5 0.22 0.458 0.309 0.619 0.536 0.951 start from level 8 0.5 0.714 0.507 0.707 0.588 0.753 start from level 7 0.255 0.381 0.353 0.541 0.588 0.828 start from level 6 0.365 0.582 0.470 0.758 0.730 1.081 outlier ratio 0.10~0.15

start from level 5 0.429 0.737 0.533 0.904 0.796 1.234

B. Face Template Matching

We perform face template matching experiments in a face-only database [27], which can be used for the application of finding a particular person in a database. We use 1000 images of 100 persons, where each person has 10 images with distinct poses or expressions per person. Each image size is normalized to be 64x64 and part of this subset is shown in Figure 6(a). For each person, we randomly select one of his (or her) images to be the test image, and the other 9 images remain in the database. Hence, there are a total of 900 images contained in the database in our experiment. All test images are contaminated by pepper-and-salt noise that is used as outliers, with the outlier ratios varying from 0 to 0.15. Figure 6(b) shows the contaminated images of a person with different outlier ratios. Such an experimental setup is similar to that shown in [24], but in our case the templates are polluted with outliers. Given a test image, we match it with the 900 images contained in the database and find the most similar one with the least sum of robust differences. The person with respect to the most similar image is then served as the recognized one. The matching experiment is performed for all of the 100 test images, and the average recognition rate (i.e. the hit ratio) is recorded.

Four different robust estimators, Huber’s estimator, Tukey’s estimator, Geman and McClure’s estimator, and the trimmed mean M-estimator, are used in this experiment. Based on (15), the parameter σ used in these estimators was determined by performing several random matches to

estimate _i

i r

median in advance. The associated 2-pyramids are constructed based on these robust estimators to speed up the corresponding robust template matching processes. First, we compare the recognition performances of template matching, using the above four robust estimators to that using the SSD criterion. Figures 7(a), 8(a), 9(a), and 10(a) show the comparison results for Huber’s estimator, Tukey’s estimator, Geman and McClure’s estimator, and the trimmed mean M-estimator, respectively. From these figures, the hit ratios obtained using SRD are generally better than those obtained using SSD, no matter which estimators are used. In particular, the hit ratios obtained by using Tukey’s estimator and Geman and McClure’s estimators consistently perform better than those using SSD in all experiments, no matter which outlier ratios are tested. This observation also confirms that the M-estimator can deal with outliers better.

In the following, we present the speedup performances of our method. In particular, we focus on the time consumption ratios in this experiment. Since the pyramids of the images contained in the database are constructed offline for this application, the pyramid-construction time for the images contained the database is not included in the time consumption ratio in this experiment. However, note that the pyramid construction time of the test image has remained to be included in the computation of time consumption ratios. The time consumption ratios of the above four robust estimators are shown in Figures 7(b), 8(b), 9(b), and 10(b), respectively. From these figures, it can be seen that our method can increase the efficiencies for the face template matching for different kinds of robust estimators. In essence, the smaller is the outlier ratio, the better speedup is achieved. In particular, the speed performances depend on what kind of robust estimators are used. For example, the speedup performances are better when Huber’s estimator, Tukey’s estimator, and the trimmed mean M-estimator are used, than that when Geman and McClure’s estimator is used. A possible reason for this is that the lower bounds derived for the former estimators are tighter than those for the latter.

C. Motion Estimation

In the last experiment, we use our method for robust motion estimation in a sequence of images. Each image in the sequence is segmented into a set of blocks, and we try to find the motion vector for each block. Assume that one image in the sequence is polluted with outliers, and the robust template matching technique is used for motion estimation when outliers occur. The Salesman image sequence is used as a test sequence where each frame is of size 352×288. Two different block sizes (16×16 and 32×32) and their corresponding search ranges (about twice as large as the block size, [-16,16] × [-16,16] and [-32,32] × [-32,32]) are tested in this experiment. Given a pair of two consecutive frames, where one is polluted as shown in Figure 11, we use the simple truncation (10) as the robust error measure for robust template matching to find the motion vectors. The time

consumption ratios (that consider all the computational overheads) and the operation count ratios are shown in Figure 12, respectively. The experimental results show that our method can also improve the efficiency for robust motion estimation.

V. Discussion

From the experimental results, the efficiency improvement of our method improves if the outlier ratio gets smaller. In fact, the time-consumption ratio may exceed a value of one in our experiment when the outlier ratio is too large, which means that our method cannot speed up the matching process in this case. However, since the estimation problem is itself more difficult to solve accurately when the outlier ratio is too large, our method can be treated as dealing with common cases of robust template matching when M-estimators are used.

One possible means to allow large outlier ratios is to make the lower bounds tighter. In fact, the set of ascending lower bounds (accompanied with the minimal feasible value and the p-pyramid structure) derived in this paper is generally available for all non-decreasing robust error measures.

Improvement is thus possible by tightening the lower bounds for a particular error measure, although the improved set of lower bounds may not be able to be used for other error measures. To achieve this goal, we can take advantage of the specific mathematical form of each of the error measures and derive new theoretical bounds and pyramid structures. Such an improvement remains an open problem and to be investigated in the future.

Our main algorithm was presented to tackle the matching problem with translation. When dealing with a problem with rotation or scaling, a useful strategy is to generate a set of templates by rotating and scaling the pattern to be matched in advance [21][37]. In this case, a p-pyramid can be produced for each template and our algorithm can then be applied for speeding up the matching process with these templates. Such a pre-transforming/pre-storing process is suitable for applications where offline processing is allowed, such as the face-matching task shown in the experimental results of this paper. Another way for dealing with rotation (or illumination variation) is to use rotationally invariant (or lighting-invariant) features such as moment invariants [10]. By this way, the templates need to be pre-processed to extract their invariant feature vectors. To our best knowledge, however, there is no analysis about the sensitivities of the invariant vectors to outliers, and thus it is possible that they are not robust enough for matching with outliers. Nevertheless, when the noise model is Gaussian and a common SSD measure is applied for matching the feature vectors, our method can also be used to speed up the matching process by building the 2-pyramids associated with the invariant feature vectors in advance. ⁶ In addition, another widely- used way for dealing with

6 Note that extraction of moment invariants can itself be speeded up with some other fast algorithms [9].