有限長度之圓柱形粒子在圓柱管中之電泳(2/3)

行政院國家科學委員會專題研究計畫 期中進度報告

有限長度之圓柱形粒子在圓柱管中之電泳(2/3)

中 華 民 國 93 年 4 月 23 日

計 畫 執 行 概 要 本 計 畫 目 前 進 展 順 利 ， 已 完 成 主 要 的 理 論 推 導 、 主 控 方 程 式 的 求 解 、 及 相 關 之 數 值 模 擬 與 分 析 。 後 附 資 料 為 目 前 已 獲 得 之 部 份 結 果 。 摘 要 本 文 中 吾 人 探 討 了 兩 相 同 圓 柱 粒 子 在 一 不 帶 電 的 圓 柱 管 中 ， 在 低 電 位 與 弱 外 加 電 場 的 條 件 下 延 其 軸 心 之 電 泳 。 這 種 幾 何 形 狀 的 安 排 使 吾 人 可 以 同 時 探 討 邊 界 效 應 與 粒 子 間 作 用 對 電 泳 的 影 響 。 數 值 模 擬 的 結 果 顯 示 ， 當 粒 子 周 圍 電 雙 層 的 厚 度 與 粒 子 間 距 離 接 近 時 ， 粒 子 間 的 作 用 對 電 泳 的 影 響 將 相 當 可 觀 。 不 過 ， 這 個 效 應 又 不 及 邊 界 效 應 來 的 重 要 。 吾 人 証 實 ， 粒 子 表 面 帶 電 不 均 勻 時 的 邊 界 效 應 較 粒 子 表 面 帶 電 均 勻 時 者 重 要 。 另 外 ， 兩 圓 柱 粒 子 間 之 作 用 對 其 電 泳 的 影 響 較 兩 球 形 粒 子 間 者 為 顯 著 。

I. Introduction

the role that a boundary can play in electrophoresis is an interesting but nontrivial problem. Compared with the electrophoresis of an isolated entity, that when a physical boundary is present is of complicated nature in that the entity-boundary interaction needs to be considered which can lead to unintuitive result. In a study of the electrophoresis of a spherical particle in a spherical cavity, for example, Hsu et al.,1 concluded that while the closer the particle-cavity distance the smaller the electrophoretic mobility of the sphere, the reverse can be true when that distance is shorter than a critical value. The latter was elaborated by that if both particle and cavity are maintained at constant electrical potential, charge reversal might occur on the latter. Keh and Chen2 considered the electrophoresis of a sphere parallel to a plane under the conditions of thin double layer. They showed that, for moderate to large separations between particle and plane, the presence of the plane has the effect of reducing the electrophoretic mobility of the particle, but the reverse is true if a particle is sufficiently close to a plane. Similar behavior was also observed by Keh et al.3 in an analysis of the electrophoresis of an infinite cylinder parallel to a plane, where they showed that the closer the cylinder to the plane, the larger its electrophoretic mobility. These observations can be explained by that the presence of the plane affects the electrical force and the viscous force acting on a particle in opposite direction, and the observed phenomenon is the net result of two competing effects. In a study of the electrophoresis of a sphere in spherical cavity, Zydney4 concluded that the boundary effect for the case of thick double-layer is much more significant than that for the case of thin double layer. Also, the charge on a cavity could alter the direction of particle movement through inducing charge on its surface and through generating an electroosmotic recirculation flow. Other relevant analyses include, for instance, those

reported by Ennis and Anderson5 and Shugai and Carnie6 for the cases of a sphere parallel to a plane, normal to a plane, and along the axis of a cylindrical pore. In fact, when a boundary is present the electrophoretic behavior of an entity is influenced by several key factors such as the increase in the viscous drag, the enhancement of the local electric field on particle surface, and the effect of possible electroosmotic flow, which can be significant if the boundary is charged.

Similar to the effect arising from the presence of a boundary, the existence of nearby entities can also have an important influence on the electrophoretic behavior of an entity. The latter occurs, for instance, when electrophoresis is conducted on a concentrated dispersion where the interaction between neighboring entities needs to be considered. Several efforts have been made to interpret the electrophoretic behavior of a particle under the influence of other particles, such as two spheres in an infinite medium7-10 and multiple spheres in an infinite medium.11-14 These studies concluded that for thin double layers, particle-particle interaction has a relatively weak effect on the electrophoretic mobility of a particle, but if double-layer polarization is important, it can be significant. Shugai et al.15 considered the electrophoresis of two spheres, which can have different charged conditions and sizes, in an infinite medium for the case of thick double layers. They concluded that the effect of particle-particle interaction on the electrophoretic mobility of a particle can be significant when the thickness of the double layer surrounding it is comparable to its radius.

The electrophoretic behavior of a particle also depends largely on the distribution of charge over its surface. It is not uncommon in practice that the charged condition on the surface of particle is of non-uniform nature. The charge on the basal plane of a kaolin particle, for example, can have a different sign from that on its facial plane. Apparently, an analysis, which is capable of taking this effect into consideration, is

desirable from practical point of view. In a study of the electrophoresis of a charged circular disk of zero thickness in an infinite medium, Sherwood and Stone16 found that if the double layer surrounding the particle is thin, the contribution of its edge charge to its electrophoretic velocity is more important that that of its surface charge.

In this study, the effects of particle-particle interaction and particle-boundary interaction on the electrophoretic behavior of a particle are examined simultaneously by considering the electrophoresis of two cylindrical particles with a moderate thick electrical double layer along the axis of an uncharged cylindrical pore under the conditions of low electrical potential and weak applied electric field. The influences of the key parameters of the system under consideration on the electrophoretic mobility of a particle are investigated through numerical simulation. These include the thickness of double layer surrounding a particle, the aspect ratio of a particle, the distance between two particles, and the ratio (particle radius/pore radius). The effect of the charged conditions on a particle is also discussed.

II. Theory

Let us consider the problem illustrated in Figure 1, where two identical, rigid, non-conducting, cylindrical particles of radius and length are located on the axis of a cylindrical pore of radius b. The surface-to-surface distance between particles is 2 . A uniform electric field E with strength E in the z-direction is applied, and the particles move along the axis of the cylindrical pore with the same velocity. The cylindrical coordinates (r,θ,z) with its origin located at the center between two particles are chosen. Because the present system is symmetric about θ only the (r,z) domain needs to be considered.

a 2d

The electrophoretic behavior of the particles is described by the electrokinetic equations, which include the equation for the conservation of ions, that for the electrical field, and that for the flow field. At steady state, the conservation of the ions leads to 0 =             ∇ + ∇ − ⋅ ∇ Ψ T k n ez n D n B i i i i iu (1)

In this expression, ∇ is the gradient operator, ni, Di, and zj are respectively the number concentration, the diffusivity, and the valence of ionic species i, e is the elementary charge, Ψ is the electric potential, kB is the Boltzmann constant, T is the absolute temperature, and u is the fluid velocity. It can be shown that on the basis of Gauss law, the electrical field can be described by the Poisson equation

ε ρ − = ∇ Ψ2 (2)

where ε is the permittivity of the liquid phase, and

∑

i i i

en z

=

ρ is the charge density of mobile ions. For the case of incompressible fluid with constant physical properties at a low Reynolds number, the flow field can be described by

Ψ ∇ = ∇ − ∇ ρ η 2u p (3) 0 = ⋅ ∇ u (4)

where η is the fluid viscosity, and p is the pressure.

Suppose that the applied electric field is weak and the surface potential of particle is low. In this case the effect of double layer polarization is negligible, the electrophoretic motility of a particle is independent of the drag coefficients of ionic species, and the equations governing the electric field and the flow field can be decoupled. Following the treatment of Henry,17 Ψ is decomposed into the electrical potential in the absence of the applied electric field, that is, the equilibrium potential arising from the presence of particles, Ψ₁, and that outside particles arising from the applied electric field, Ψ2. In the absence of the applied electric field n

)

T

i can be obtained by letting u=0 in eq 1 and solving the resultant expression to obtain

, n /

exp( ₁

0 ez k

n

n_i = _i − _iΨ _B i0 being the bulk number density of ionic species i. Under the conditions of low surface potential, Ψ₁ can be described approximately by the linearized Poisson-Boltzmann equation

1 2 1 2Ψ =κ Ψ ∇ (5) where (e2 z2n₀/ k_BT)1/2 i i i ε

κ =

∑

the Laplace equation

0

2 2 =

If both the basal and the lateral surfaces of a particle are uniformly charged with densities σ₁ and σ₂ respectively, then the boundary conditions associated with eqs 5 and 6 can be expressed as

ε σ1 1 − = ∇ ⋅ Ψ n and 2 =0 ∂ ∂ z Ψ , z =h, z =h+2d, 0≤r≤a (7) ε σ₂ 1 − = ∇ ⋅ Ψ n and 2 =0 ∂ ∂ r Ψ , r =a, h≤ z ≤h+2d (8) 0 1 = ∇ ⋅ Ψ n and 2 =0 ∂ ∂ r Ψ , r=b (9) 0 1 = Ψ and ∇Ψ₂ =−E, z →∞, r<b (10)

In these expressions n is the unit normal vector directed into the liquid phase.

Suppose that both the surface of particle and that of pore are no-slip. Then if U is the magnitude of particle velocity in the z-direction, the boundary conditions associated with eqs 3 and 4 can be expressed as

z i u=U on particle surface (11) 0 = u , r=b and z →∞, r<b (12)

In the present case, the forces acting on a particle include the hydrodynamic force and the electric force. The axisymmetric nature of the present problem suggests that only the forces in the z-direction need to be considered. The electric force acting on a particle in the z-direction, F_EZ, can be calculated by

∫∫ −∂_∂ = ∫∫ = S S Z Z E dS z dS E F σ σ( Ψ ) (13)

where S denotes particle surface. The hydrodynamic force acting on a particle in the z-direction, , comprises the viscous force and that arising from the hydrodynamic pressure. We have Z D F 18

∫∫

∫∫

where t and n are respectively the unit tangential and unit normal vectors on particle surface, n is the magnitude of n, and tz and nz are the z-component of t and that of n respectively. At steady state, the net force acting on a particle vanishes, that is,

0 = + Z E Z D F F (15)

The electrophoretic mobility of a particle can be evaluated through a trial-and-error procedure based on this expression. For a set of specified E, σ , 1 σ , 2 κ , a ,

and , and are evaluated by solving eqs 5 and 6, and the results obtained used to calculate by eq 13. An arbitrary U is guessed which is used

a h / d a / a /b Ψ₁ Ψ₂ Z E F

to determine the flow field through solving eqs 3 and 4, and is calculated by eq 14. The calculated and are substituted into eq 15 to see if it is satisfied. If it is satisfied, the previously guessed value of U is correct. Otherwise, a new U is guessed, and the whole procedure is repeated.

Z D F Z E F E refε Z D F ζ * µ 2 σ

FlexPDE19, a differential equation solver based on a finite element method is adopted for the resolution of the governing equations and the associated boundary conditions. This software was found to be efficient and accurate for the electrokinetic phenomena of the present type.20 For convenience, we define the scaled mobility

as , where

*

µ

Uη ζ

µ* = / _ref =k_BT /e is a reference potential. The applicability

of the numerical scheme adopted is justified by Figure 2, where the variation of as a function of λ (=a/b) at various scaled separation distance between two particles h/a is illustrated. This figure shows that the result for the case when only one cylinder is present in pore20 can be recovered as a limiting case of the present analysis as h/a is large.

III. Results and Discussions

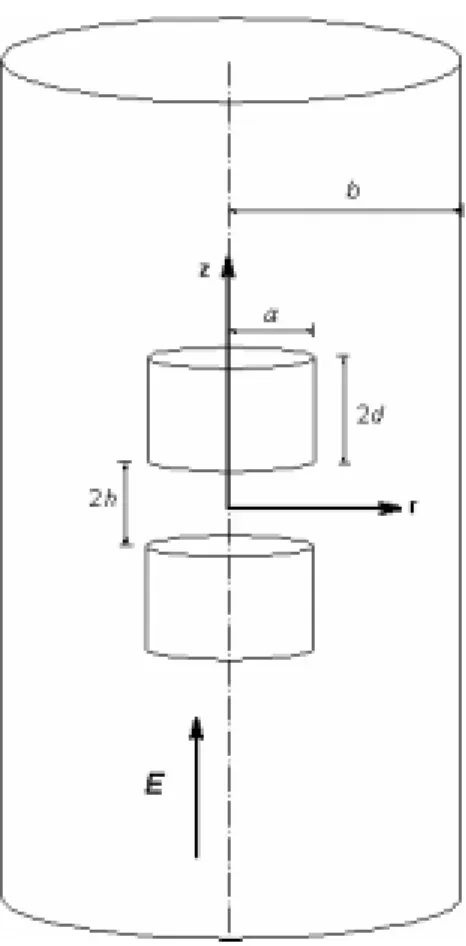
For the present problem, if both σ and ₁ are known, the mobility is a function of κ , h/a, a/d and a/b. Figure 3 shows the variation of the scaled electrophoretic a

mobility as a function of the scaled separation distance between two particles, h/a, at various combinations of

*

µ

λ and κ for the case of uniformly charged particles. a

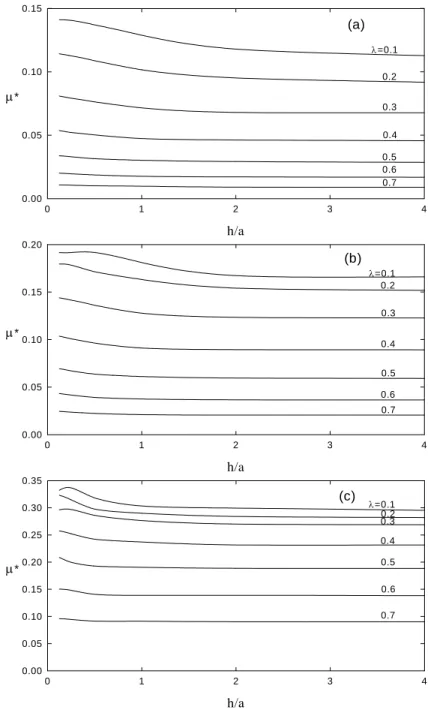
The corresponding results for the case of non-uniformly charged particles are illustrated in Figure 4. Figure 3 indicates that, if h/a is sufficiently large, approaches a constant value, which is the result for the case when only a particle is present in the pore. Similar to the result for the case of a pair of identical spheres in *

an unbound fluid,15 the influence of the interaction between the double layers surrounding the particles is inappreciable if κ is large, but becomes significant if a

a

κ is small. For example, if λ=0.1, the maximum differences of from that for the case of an isolated sphere in a pore are 12, 15, and 25﹪for

* µ 4 = a κ , 1, and 0.5 respectively. The dependence of on h/a is more sensitive to that for the case of two identical spheres in an unbound fluid.

*

µ

15

This dependence becomes insignificant, however, if λ is large, because the viscous drag arising from the wall dominates. It can be inferred that the dependence of on h/a for the case of two cylinders in an unbound fluid is much more sensitive to that for the case of two spheres because the interaction between the double layers surrounding two particles is more significant in the former. Figure 3 also indicates that the smaller the

*

µ

a

κ (thicker double layer), the smaller the , and the larger the h/a needed to reach a constant value. The former is because the thicker the double layer, the greater the hydrodynamic retardation force arising from the access ions and the boundary, and the latter is because a larger separation distance between two particles is required to avoid double layer interaction. Note that because the double layers surrounding the particles begin to overlap when

*

µ

h

κ reaches unity, double layer interaction is significant when κh≤1. In general, decreases with the increase in

*

µ λ , which is expected because the larger the λ , the more significant is the viscous drag arising from the presence of cylindrical pore. It is interesting to note that while decreases with the increase in h/a, in general, a local maximum may occur if

*

µ

a

κ is sufficiently large and λ is sufficiently small. This phenomenon was also observed for the case of two spheres in an unbounded fluid.15 The occurrence of the local maximum is the consequence of the competition between two opposing effects: (1) the strength of local electric field on the surface of a particle

a r

z ₌

∂ ∂ / )

( Ψ2 , and therefore, the electric force acting on it, decreases with the decrease

in h/a, and (2) the hydrodynamic retardation arising from the presence of the other particle decreases with the decrease in h/a, which is also observed in sedimentation. It should be pointed out that as two particles approach each other under the conditions of constant surface charge, the surface potential might violate the low surface potential assumption. For example, if h/a=0.0625 and κa =1, the scaled surface potential has a maximum value of 2.23~3.36 for λ =0.1~0.8. As can be seen in Figure 4, the qualitative behaviors of for non-uniformly charged particles are similar to those of uniformly charged particles. A comparison between Figures 3 and 4 reveals that if

*

µ

λ is small, the rate of decrease of as h/a increases for non-uniformly charged particles is faster than that for uniformly charged particles. For example, if

* µ 1 . 0 = λ ,

the maximum differences of from that for the case of an isolated sphere in a pore are 15, 26, and 29% for

*

µ

4 =

a

κ , 1, and 0.5 respectively; these differences are larger than that for the case of uniformly charged particles. This implies that the interaction between two particles for the case of non-uniformly charged particles is stronger than that for the case of uniformly charged particles. If λ is large, because the boundary effect of pore dominates, the influence between particles on becomes unimportant. A comparison between Figures 3(a) and 4(a) indicates that at

* µ 5 . 0 = a κ , if λ is small (0.1-0.2), for non-uniformly charged particles is larger than that for uniformly charged particles; but the reverse is true if

*

µ

λ is large (0.4-0.7). This implies that the boundary effect for the case of non-uniformly charged particles is more significant than that for the case of uniformly charged particles. This will be discussed later.

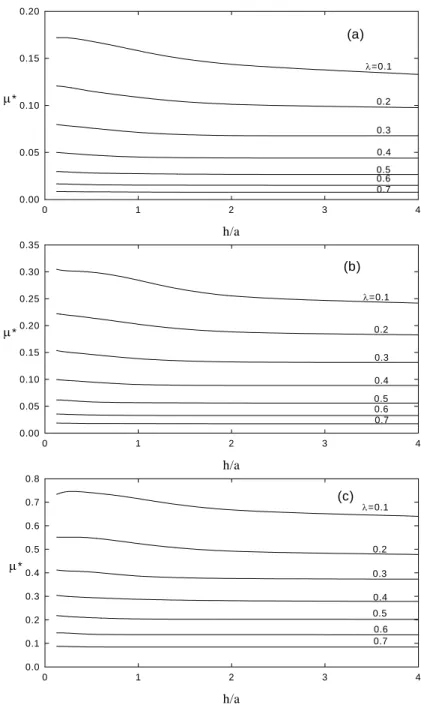
The variations of the scaled electrophoretic mobility µ* as a function of λ for various combinations of a/d and κ are presented in Figure 5 for the case of a

uniformly charged particles. This figure reveals that while decreases with the increase in

*

µ

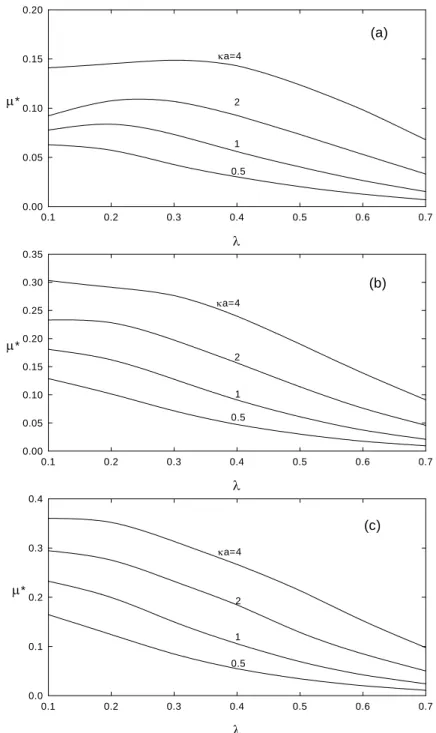
λ , in general, µ* may have a local maximum as λ varies if a/d is sufficiently large. This phenomenon was also observed in the case of the electrophoresis of a single cylinder in a cylindrical pore.20 For the present case, it can be explained by the behaviors of the forces acting on a particle illustrated in Figure 6. As can be seen in Figure 6(a), for uniformly charged particles, the electric force acting on a particle increases monotonically with λ , and the hydrodynamic force acting on it may have a local minimum as λ varies. The former is mainly because that if a particle is close to pore, the squeeze of the applied electric field near particle surface leads to an increase in the electric force. The latter arises from the complicated effects of the combination of the space charged density and the strength of local electric field between particles and boundary on the hydrodynamic force as λ varies. For the case of non-uniformly charged particles, the hydrodynamic force acting on a particle does not have a local minimum, as shown in Figure 6(b), which implies that decreases monotonically with the increase in

*

µ

λ , which is justified in Figure 7. A comparison between Figures 5 and 7 indicates that the variation of µ* as λ varies for the case of non-uniformly charged particles is more drastic than that for the case of uniformly charged particles. This is consistent with previous observation, that is, the boundary effect on for the case of non-uniformly charged particles is more significant than that for the case of uniformly charged particles.

*

µ

*

µ

λ

Figure 8 shows the variation of the scaled electrophoretic mobility as a function of for the case of Figure 5. This figure suggests that the larger the a/d the smaller the . For a fixed , a large a/d implies a small lateral surface of a particle, and therefore, a small amount of surface charge. The former leads to a small

*

hydrodynamic retardation by shear force, and the latter yields a small electric force. In the present case, because the decrease in the electric force is larger than that in the hydrodynamic retardation as a/d increases, decreases accordingly. Figure 9 shows the variation of the scaled electrophoretic mobility as a function of

*

µ

*

µ λ for

the case of non-uniformly charged particles. This figure reveals that, if the double layer is sufficiently thick (κa=0.5 and 1), the dependence of on a/d is similar to that for the case of uniformly charged particles illustrated in Figure 8. However, for a sufficiently thin double layer (

*

µ

a

κ =4), the behavior of as a/d varies shows a different result from that described above when

*

µ

λ is small. That is, if λ is small (boundary effect unimportant), may have a local maximum as a/d varies, and it is expected to decreasing to that of uniformly charged particles as a/d 0. The former is a net result of the competing effects between electric force and hydrodynamic retardation described in the discussion on Figure 8 as a/d varies, and the later is due to the fact that the contribution of the charge on the basal surface of a particle can be ignored when its length approaches infinite.

*

µ

→

IV. Conclusion

In summary, the boundary effect, the presence of other particle, and the charged conditions on a particle on its electrophoretic behavior are examined simultaneously by considering the electrophoresis of two identical cylindrical particles along the axis of an uncharged cylindrical pore. The results of numerical simulation reveal the followings: (a) The dependence of the mobility of a particle on the separation distance between two particles is more sensitive to that for the case of two identical spheres in an unbound fluid. This dependence becomes insignificant, however, if the boundary

effect is significant. (b) The effect of particle-particle interaction on the mobility of a particle becomes significant when the thickness of the double layer surrounding a particle is comparable to half the separation distance between two particles, but this effect is less significant than the boundary effect, which is closely related to the charged conditions on a particle. The boundary effect for the case of non-uniformly charged particles is more significant than that for the case of uniformly charged particles. (c) While the mobility of a particle decreases with the increase in the separation distance between two particles, in general, a local maximum may occur if the double layer is sufficiently thin and the boundary effect is relatively unimportant. (d) If the boundary effect is relatively unimportant, the rate of decrease in the mobility of a particle as the separation distance between two particles increases for non-uniformly charged particles is faster than that for uniformly charged particles. (e) For uniformly charged particles, while the more significant the boundary effect the smaller the mobility, in general, the mobility may have a local maximum if the particle aspect ratio is sufficiently large. The mobility of a particle increases with the increase in its aspect ratio. (f) For non-uniformly charged particles, if the double layer is sufficiently thick, the dependence of the mobility on the particle aspect ratio is similar to that for the case of uniformly charged particles. However, if the double layer is sufficiently thin and the boundary effect is relatively unimportant, the mobility may have a local maximum as the particle aspect ratio varies.

Acknowledgment

References and Notes

(1) Hsu, J. P.; Hung, S.H.; Kao, C. Y. Langmuir 2002, 18, 8897.

(2) Keh, H. J.; Chen, S. B. J. Fluid Mech. 1988, 194, 377.

(3) Keh, H. J.; Horng, K. D.; Kuo, J. J. Fluid Mech. 1991, 231, 211.

(4) Zydney, A. L. J. Colloid Interface Sci. 1995, 169, 476.

(5) Ennis, J.; Anderson, J. L. J. Colloid Interface Sci. 1997, 185, 497.

(6) Shugai, A. A.; Carnie, S. L. J. Colloid Interface Sci. 1999, 213, 298.

(7) Reed, L. D.; Morrison, F. A. J. Colloid Interface Sci. 1976, 54, 117.

(8) Keh, H. J.; Chen, S. B. Am. Insti. Chem. Engr. J. 1988, 34, 1075.

(9) Keh, H. J.; Chen, S. B. J. Colloid Interface Sci. 1989, 130, 542.

(10) Keh, H. J.; Chen, S. B. J. Colloid Interface Sci. 1989, 130, 556.

(11) Keh, H. J.; Yang, F. R. J. Colloid Interface Sci. 1990, 139, 105.

(12) Keh, H. J.; Yang, F. R. J. Colloid Interface Sci. 1991, 145, 362.

(13) Chen, S. B.; Keh, H. J. J. Fluid Mech. 1992, 238, 251.

(14) Keh, H. J.; Chen, J. B. J. Colloid Interface Sci. 1993, 158, 199.

(15) Shugai, A. A.; Carnie S. L.; Chan, D. Y. C.; Anderson, J. L. J. Colloid Interface Sci. 1997, 191, 357.

(16) Sherwood, J. D.; Stone, H. A. Phys. Fluid. 1995, 7, 697.

(18) Backstrom, G. Fluid Dynamics by Finite Element Analysis; Studentlitteratur: Sweden, 1999.

(19) FlexPDE version 2.22, PDE Solutions Inc., Scranton, PA.

Figure 1. Schematic representation of the problem considered. Two charged cylindrical particles with a separation distance 2h are placed on the axis of an infinite cylindrical pore of radius b. An electric field E parallel to the axis of the pore is applied. The cylindrical coordinates (r,θ,z) are adopted with its origin located at the center two particles. 2a and 2d are respectively the axes of the particle in the r- and in the z-directions.

λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 0.25 (a) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 h/a=1/8 1 4 (b) h/a=1/8 1 4

Figure 2. Variation of scaled mobility µ* as a function of λ at various scaled separation distance between two particles h/a for the case when κa=1, and a/d=1. (a)

) / ( 5 . 0 2 1 σ εκkBT e

σ = = , (b) −σ₁ =σ₂ =0.5(εκk_BT /e) . Discrete symbols are the results for the case when only one cylinder is present in a cylindrical pore.20

(a) h/a 0 1 2 3 4 µ* 0.00 0.05 0.10 0.15 (b) h/a 0 1 2 3 4 µ* 0.00 0.05 0.10 0.15 0.20 (c) h/a 0 1 2 3 4 µ* 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 λ=0.1 0.2 0.3 0.5 0.6 0.7 0.4 λ=0.1 λ=0.1 0.2 0.3 0.6 0.5 0.4 0.7 0.2 0.3 0.6 0.5 0.4 0.7

Figure 3. Variation of scaled mobility µ* as a function of at various

a

h / λ and κa

for the case when a/d=1, and σ₁ =σ₂ =0.5(εκk_BT/e). (a) κa=0.5, (b) κa=1, (c)

a

(a) h/a 0 1 2 3 4 µ* 0.00 0.05 0.10 0.15 0.20 (b) h/a 0 1 2 3 4 µ* 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 (c) h/a 0 1 2 3 4 µ* 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 λ=0.1 0.2 0.3 0.5 0.6 0.7 0.4 λ=0.1 λ=0.1 0.2 0.3 0.6 0.5 0.4 0.7 0.2 0.3 0.6 0.5 0.4 0.7

Figure 4. Variation of scaled µ* as a function of h/a for the case of Figure 3 except that

) / ( 5 . 0 2 1 σ εκkBT e σ = = − . (a) κ =0.5, (b) a κ =1, (c) a κ =4. a

(c) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.0 0.1 0.2 0.3 0.4 κa=4 2 1 0.5 (b) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 κa=4 2 1 0.5 (a) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 κa=4 2 1 0.5

Figure 5. Variation of scaled mobility µ* as a function of λ at various combinations of

a/d and aκ for the case when h/a=1, and σ₁ =σ₂ =0.5(εκk_BT/e). (a) a/d=4, (b) a/d=1, (c) a/d=0.5.

λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 FD Z * or F E Z * 0 50 100 150 200

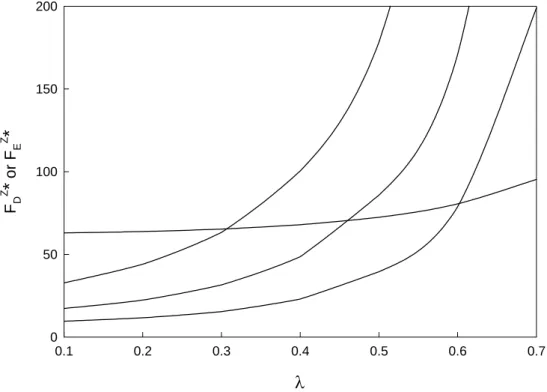
Figure 6. Variation of scaled hydrodynamic force ( ) and scaled electric force ( ) acting on a particle at various as a function of

* Z D F F n kBT Z D / 10 = * µ * Z E F F n kBT Z E / 10 = λ

for the case when κa =4, h/a =1, and a/d=4. (a) σ1 =σ2 =0.5(εκkBT/e), curves 1, 2,

and 3 correspond respectively to µ* =0.20, 0.17, and 0.15. (b)

) /e T B ( 5 . k 0 2 1 σ εκ σ = =

− , curves 1, 2, and 3 correspond respectively to =0.4, 0.2, and 0.1.

*

(c) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.0 0.2 0.4 0.6 0.8 κa=4 2 1 0.5 (b) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.0 0.2 0.4 0.6 0.8 κa=4 2 1 0.5 (a) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.0 0.2 0.4 0.6 0.8 κa=4 2 1 0.5

Figure 7. Variation of scaled mobility µ* as a function of λ for the case of Figure 5 except that −σ₁ =σ₂ =0.5(εκk_BT/e). (a) a/d=4, (b) a/d=1, (c) a/d=0.5.

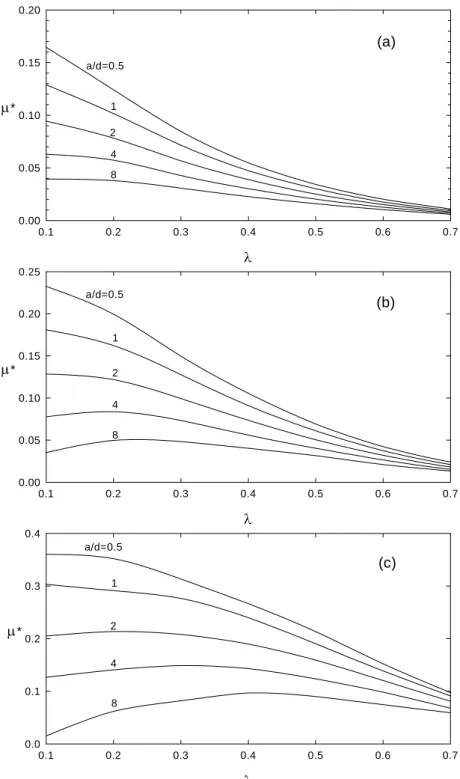
(a) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 a/d=0.5 1 2 4 8 (b) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 0.25 a/d=0.5 1 2 4 8 (c) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.0 0.1 0.2 0.3 0.4 a/d=0.5 1 2 4 8

Figure 8. Variation of scaled mobility µ* as a function of λ at various combinations of

a/d and aκ for the case when h/a=1 and σ₁ =σ₂ =0.5(εκk_BT/e). (a) aκ =0.5, (b)

a

(a) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 a/d=0.5 1 2 4 8 (b) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 a/d=0.5 1 2 4 8 (c) λ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 µ* 0.0 0.2 0.4 0.6 0.8 a/d=0.5 1 2 4 8 λ 0.10 0.15 0.20 µ* 0.5 0.6 0.7 0.8 a/d=0.5 4 2 8 1

Figure 9. Variation of scaled mobility µ* as a function of λ for the case of Figure 8 except that −σ₁ =σ₂ =0.5(εκk_BT/e). (a) κ =0.5, (b) a κ =1, (c) a κ =4. a