EGECIOGLU. O., and KOC'. K : 'Exponentiation using canonical recoding', Theoretical Computer Science, 1994, 129, (2), pp. 407- 417
KAI-HWANG: Computer arithmetic, principles, architecture, and design' (John Wiley & Sons, New York, 1989)
KOREN, U , : 'Computer arithmetic algorithms' (Prentice-Hall, Englewood Cliffs, NJ, 1993)
LADNER, R . , and FISCHER. M.: 'Parallel prefix (computation', J . A C M . 1980, 27, (4), pp. 831-838
REITWIESNEK, G.w.: 'Binary arithmetic', Advances in Computers,
1960, 1, pp. 231-308
where, from the results in [4], the coefficients ai/<, and aiiiz are given by
2D multiple notch filter design
Chien-Cheng Tseng and Soo-Chang Pei
Indexing terms: Notch filters, Two-dimensional tligitul filters The authors propose a decomposition method to reduce the 2D multiple notch filter design problem to two pairs of ID filter design problems. They develop a simple algebraic method for the design of two pairs of 1D TIR filter design. This approach not only has closed form transfer function but also satisfies the bounded inputioutput (BIBO) stability condition.
Introduction: Notch filters are an effective means for eliminating narrowband or sinusoidal interferences in certain :signal processing applications ranging from power line interference cancelation for electrocardiograms to mukipk sinusoidal interference removal for corrupted images. For the 1D case, several methods for the design and performance analysis of IIR and FIR notch filters have been developed, see [I - 31 among others. For the 2D case, [4] proposed a method that reduces the design of a 2D single notch filter to the design of a 2D parallel line filter and a 2D straight line filter. However, a technique for designing a 2D multiple notch filter has not yet been developed. In this Letter, we address this design problem.
Design technique: The frequency response of an ideal 2D multiple notch filter is given by
0 1 otherwise ( q , w2) = (wqk, wGk) and (- * I:. b - - 1 ,...,
N
H , l ( e J w l , e 7 w 2 ) ={
d l k > (1) where (ark, a;,) are the notch frequencies. The aim of this work is to find a stable 2D transfer function which satisfies this specifica- tion. Our design technique is mainly based o'n the following decomposition of the frequency response of an ideal notch filter:Fact 1: Given that two l D filters H)t(zJ and H f l ( z J have the following frequency responses ( i = 1, 2):
-3 w, = w;k
{
0 otherwiseH;,(e3"?) = 3 W, = -wrk ( 3 )
then the frequency response of an ideal 2D multiple notch filter can be written as
Hd(e3&1, eJw2) =
(4) From Fact 1, we see that the design of a 2D multiple notch fil- ter can be decomposed into two types of 1 D filter design. The first is the design of filter ff/<,(ejuJ) defined in eqn. 2, the other is the design of filter H:t(eJwt) defined in eqn. 3 ( i = 1, 2). We shall address the design of these two types of filters.
(i) Design offilter H:6(zJ: The frequency response of H':,(ejwr) can be approximated by the second-order IIR bandpass filter whose transfer function is given by
with ai is the centre frequency of Hih(z,) and BW is the 3 dB
bandwidth of H;?(zJ. Note that H,i;,(ej""J'c) is exactly equal to unity, i.e. Hk6(ejw1IL) has unit gain and zero phase at a, = ~ 0 : ~ . Thus, H;,(C?") will be an excellent approximation of H;",(eJwi) pro- vided that BW is sufficiently small.
(ii) Design of,filter H:z(z,): It can readily be verified that the filter
H!(z,) can be obtained as H:,(z,) = HCi, (zJHk,(zJ where the fre-
quency response of Hk,(zJ is given by
w, = w;k
~h a z ( $ U , ) ~= w, = -W,"i, ( 7 )
{
i:n't care otherwiseSince H;!(zJ has been designed in the preceding subsection, we now only need to design filter H!z(z,) For simplicity, we choose Hj,(z,) to be the following first order allpass filter:
Since iHt)h(e'coi)l is equal to unity for all frequencies, we have Hj,(eIW!) = e/ein(wi) where the phase response 0,,(0,) is given by
b,k sin(w,) 1
+
b,k cos(w2)H,I, (U,) = -dz
+
2 arctan Also, the specification in eqn. 7 implies thatSubstituting eqn. 10 into eqn. 9, we obtain sin(+ -
2)
btk = I
+ E
2 4
Based on the above discussion, a complete procedure for the design of a 2D multiple notch filter can be summarised as follows: (i) Step 1: Specify notch frequencies (a;k, a,*/,) and bandwidth BW f o r k = 1
...
N.(ii) Step 2: Use eqn. 6 to compute filter coefficients ark,, a,k2, and construct transfer functiion HiZ(za).
(iii) Step 3: Use eqn. 11 to calculate coefficients h,,, and construct
transfer function H:d(z,)
(iv) Step 4: Form the transfer function of the 2D multiple notch filter as H ( a 1 z2) = ) (1 - M -1 --1 @g
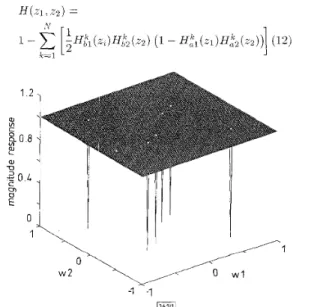
Fig. 1 Magnitude response of desipzened 2D multiple notch filter
Design exumple: In this example, three notch frequencies and
bandwidth BWare chosen as (myl, U;,) = (0.2n,0.2~), (myz, U;) = (0.3~,0.4n), (ai?, a;,) = (-0.6~,0.6~). B W = 0 . 0 0 1 ~ . Fig. 1 shows the magnitude response of the designed multiple notch filter in lin- ear scale. It is clear that the specification is well satisfied. In fact, when the bandwidth B W approaches zero, the designed multiple
notch filter will become an ideal one.
Conclusiorzs; In this Letter, a 2D multiple notch filter design prob-
lem has been investigated. First, we reduce the 2D notch filter design problem to two pairs of 1D filter design problems. Sec- ondly, we provide the closed-foiin solutions for the design of two pairs of ID IIR filters.
0 IEE 1996
Electronics Letters Online No: 19961385
Chien-Cheng Tseng (dpplied Research Laboratory, Telecommunication Luboratories, Clzungliua Telccont Co., Ltd,, Yung Mei, Taiwan, Republic of China)
Soo-Chang Pei (Dejmrtment of Electricid Engineering, Nntional Taiwan University, Taipei, Taiwan, Republic o j Chinu)
8 Augu.rt 1995
References I 2
ER. M . H : 'Designing notch filter with controlled null width", Signal Process., 1991, 24, ( 3 ) , pp. 319-329
M E D L I N , G w : 'A novel design technique for tuneable notch filters'. Proc. hit. Symp. on Circuits and Systems, New Orleans, Louisiana, USA, 1990, I , pp. 471-474
DlJTTA ROY, S C , JAIN. S B.. and K U M A R . B : 'Design O f digital FIR notch filters', IEEE Proc.- Vi.c. Image Signal Proce.ss., 1994. 141, 4 SOO-CHANG PEI, and CHIEX-CHENG T S ~ N G : 'Two dimensional IIR digital notch filter design', IEEE Truiis. Cilcuits and Syst.-11, 1994, C A S 4 1 ,
(9,
pp. 227-2313
(5), pp. 334-338
Accurate parallel form filter synthesis
M.
Price,S.
Holden andM.
SandlerIndexing ternzs: Digital filters, Network synthesk
Standard algorithms for synthesising parallel form digital filters are adequate for basic applications. However, recursive filters required in acoustics synthesis applications often have very high orders, and errors Cram filter synthesis can become intolerable. The authors describe a new method for synthesising parallel fomi recursive fillers. In the experiment described, the new algorithm yielded smaller errors than the standard technique for almost every filter tested.
Introduction: In acoustics synthesis applications, the recursive syn- thesis filter transfer function is usually specified in its direct form as the rational function, defined in eqn. 1:
where Q(z) and U(z) are assumed to be known, with degree[Q(z)] =
N
and degree[U(z)]
= M .However, it is useful to implement the synthesis filter with a parallel form: so that each resonance can be independently con- trolled [2]. The filter is converted into a parallel form by decom- posing the transfer function into a sum of rational functions, as defined in eqn. 2:
(2) where 15 the sum of the number of real poles and the number of
complex pars of poles, and x,* = 0 when x, is real. This is usually achieved by computing the partial fraction decomposition, and recombining the terms that involvc complex conjugate pairs of poles
The standard numerical algorithm for coniputing a partial frac- tion decomposition is known as 'direct determination of principal- parts' (DDPP) [l]. Despite its relatively low computational com- plexity, we have found that the DDPP method yields large errors when synthesising high order filters ( N t 8), such as those required in acoustics synthesis applications.
In this Letter, we define a new parallel form synthesis algo- rithm, and compare it with the DDPP method. The comparison i s made using Monte-Carlo techniques.
New parallel f o r m synthesis ulgoritlim: This algorithm i s a general- isation of the 'undetermined coefficients' partial fraction expan- sion algorithm [l]. The generalisation enables us to obtain the parallel form representation directly, avoiding the use of complex arithmetic.
We begin with H(z), which is to be transformed into the parallel
form representation of eqn. 2. We assume that M < N a n d hence
So ( z ) = 0. From eqn. 2, we obtain the identity d
where Q,(z) is defined as
with Q,(z) = (1 - x,z-I)(l - xJ*zl), for j = 1, 2 , ...,
p,
and where p,= degree[Q,(z)]. The pole locations xi and
,,-
are assumed to be known.Equating coefficients of eqn. 3 for powers in z, yields a 2p order, non-singular system of simultaneous equations. In matrix form, it is
* . p = u - - (5)
UT = [?LO u,1 ' " U ( 2 D ) - ' ] ( 6 )
-
PT = b i , O Pz.O . ' . Pp.O Pl,l P 2 , l ' ' ' PA11
(7)
where
with U , = 0 for i > M ,
with P, I = 0 when pl = 1 and f o r j = 1, 2, _..,
p,
and. ' ' q 3 , O 0 ;
...
01.0 0 2 , o ' ' '
0/3,@
0 0. . '
d1,l d2,l ' . ' @p,1 01.0 pp,o 0 0 ' ' ' 0
with QJ,, = 0 for i
therefore obtained by solving eqn. 5 for E.
N - p, - 1 and f o r j = 1, 2, _ _ _ ,
p.
The coefficients of the subfilter numerator polynomials PJ(z) are
Murzte-Curlo tests: Monte-Carlo methods were applied to the problem of quantifying the average error incurred from a synthesis process as follows. 12 sets of 100 all-pole test filters, each set for a specific filter order ranging from 8th to 96th order, were gener- ated. The filters were generated by randomly placing the required number of poles within the unit circle, with a unifonn distribution. The test proceeded by computing the parallel form realisation of each test filter, using each of the synthesis methods. The errors in the resultant realisations were then measured as follows.
f i l t e r DFT H (I) 1453111
Fig. 1 Filter Jinwlation for Monte-Carlo tests
Each synthesised test filter was simulated as illustrated in Fig. 1, using double precision floating-point arithmetic. The errors in the fi-equency responses of the test filters were then measured, by coni- paring with the frequency responses of the cascade form equiva- lents, in terms of average spectral deviation, e,. This i s defined in eqn. 9: