Integrating History of Mathematics in Teaching and Learning Logarithm: A Case Study

Integrating History of Mathematics in Teaching and Learning Logarithm: A Case Study

Chung Wing Hong Patrick

Po Leung Kuk Celine Ho Yam Tong College

Usually, logarithm is introduced to students by its definition “If

= 10 ,

then = log ”. Although it is easy and straight forward for students to follow, most of students do not know why they need to learn logarithm and what is the

importance of logarithm in mathematics. By reference to the history of development of logarithm, I had tried to implement a student

-centered exploratory activity for the students in learning the concept and properties of logarithm. The lesson started from the following question:

Few students said that it is impossible to solve these equations, as it did not make sense for 10 10 10 … for times to be equal to 2 or 3! However some students recall that they have learnt

1

102 10 3.16, hence they tried to observe

the following pattern and guess that the values of should be something

between 0 and 1:

0 ? ? 0.5 ? … 1

10 1 2 3 3.16 4 … 10

At that moment the story of the mathematician John Napier and the idea of logarithm were introduced to them:

Students were curious at that moment. Afterwards a worksheet was given to them (refer to Appendix I). Since it seemed to be too difficult for students to

understand the way to find the values of log 2 and log 3 at the beginning,

x ^y

y x

“We know that if 10^x = 1, then x = 0; similarly if 10^x = 10, then x = 1. But if 10^x = 2, what will be the value of x? Moreover, how about if 10^x = 3, 10^x = 4, etc. … Can you solve these exponential equations?

x

x

x

x

“It is difficult to find the values of x in the table above, however a

mathematician called John Napier, who was born 500 years ago, had found the values of x above, without the help of computer or calculator! Finally he made it and recorded his finding into a table called Logarithm Table”

´ ´

»

=

therefore their values were given to students and I told them the values of log 2 and log 3 would be found later. Then the students were guided to find the values of log 4, log 5, etc… , as they could still remember the law of indices they had

learnt in last year, they could follow the guidelines in the worksheet

successfully and use the similar way to find the value of log 6 (refer to Figure 1).

Figure 1: Students followed the guideline to find log 4, log 5 and log 6 And we can see that the students were applying the properties of logarithm (i.e. log(M

N) = logM + logN and log(M N) = logM

–

logN) in the

worksheet, but actually those properties were not “officially” taught to them.

Students had just observed the relationship between exponential form and logarithmic form and deduced the way to manipulate logarithm by themselves.

After students had found the value of log 6, they were asked to find the value of log 7, log 8 and log 9. Most of them could find the values of log 8 and log 9 successfully, but they were frustrated in finding the value of log 7 (refer to Figure 2). Later they found that none of their classmate could find the value of log 7, and then I asked them a question:

Students were asked to express their finding in the worksheet. Most of

´ ¸

“Why is it so difficult to find the value of log 7? What is the different among the number 7 and other numbers such as 6, 8 and 9?”

them stated that 7 could not be expressed as a product of 2, 3, 4, … and some of them could point out that 7 is a prime number (refer to Figure 3). Finally they understood why it was so difficult to find the values of log 2 and log 3, since 2

and 3 were also both prime numbers (but not log 5 since log 5 could be

expressed as log(10 2) = log 10 – log 2).

Figure 2: Students tried to find log 7, log 8 and log 9

Figure 3: Students explained why it is difficult to find log 7

After the short summary, students were asked to find the values of log 11, log 12, log 13 …

to log 30. During the task, most of the students had

discovered the last properties of logarithm, which is log

=

^log (refer to

¸

M

^{n n}

M

Figure 4). Although there were some mistakes in presentation (e.g. express log 3³ into (log 3)³), it was glad to see that students could discover and apply the properties of logarithm by themselves.

Figure 4: Students tried to find different logarithm values

When students became familiar with the properties of logarithm, the

logarithm table was introduced to the students formally and straightforwardly, and they learnt how to look for a logarithm value in the table. At the same time the bibliography of Napier and the importance of logarithm table were further introduced to the students:

Students were amazed why Napier could keep working on logarithm for over twenty years (they claimed that even they loved computer games, they

would not spend 20 years on the games!). They were impressed by the

composure and enthusiasm of Napier. Afterwards more practices had been given to the students to find different values of logarithm (refer to Figure 5).

1 Full text is available at http://math.about.com/library/weekly/blbionapier.htm .

“Napier had a great interest in astronomy, which led to his

contribution to mathematics. He was involved in research that required lengthy and time consuming calculations of very large numbers. Once the idea came to him that there might be a better and simpler way to perform large number calculations, Napier focused on the issue and spent twenty

years perfecting his idea. The result of this work is what we now

calllogarithms...” ¹

Figure 5: Work on the logarithm table by students

After finding the values of log 1.21, log 1.5, log 1.92, etc., students had more practices on the property log(M N) = logM – logN. On the other hand lots of students found that the value of log 1.92 they evaluated (which was

0.2831) was slightly different from the value stated in the logarithm table

(which is 0.2833). They were frustrated since they had verified again and again and found that there were no errors in their calculation. After a short in-class discussion, some students discovered that accuracy of log 2, log 3,… given in the worksheet was not good enough (they had used calculator to clarify their finding). Then I introduced the work of another mathematician Henry Briggs, who also worked on logarithm with Napier 500 years ago. And then students were asked to follow the way of Briggs to find the value of log 2 by themselves (refer to Figure 6):

¸

Figure 6: Students tried to find the approximation of log 2

Later students knew that Briggs had found the value of 2

¹00000000000000

(which is a 30102999566399

-

digit number) in order to find a precise

approximation of log 2 = 0.30102999566398, they said that they could not believe it! They could not imagine how Briggs found the value of 2100000000000000

500 years ago, without using computer or calculator. On the other hand some students were inspired and continued to work on finding the values of log 3 and log 7 (refer to Figure 7):

Figure 7: Students found the approximation of log 3 and log 7 respectively

After the activity students were asked to complete some exercise in the

textbook. All of them could finish the exercise without major problems.

Although there was still some presentation error in their works, such as log27 = (log3)³ = 3 log3 and log2 ^{+ 1}

=

+ 1 log2, it could see that students had learnt the properties of logarithm and applied them successfully. Throughout the learning activity, the history of development of logarithm had been integrated

into the activity, but it was not the whole picture of the development of

logarithm. Actually Napier had used a geometric-kinematic scheme to obtain a well definition of logarithm (Katz, 1986, 1995), but it had not been introduced

in the lesson, because it involved abstract concept about manipulation of

arithmetic and geometric sequences, which was quite difficult to be followed by secondary four students. In order to facilitate better understand of students about

the invention and development of logarithm, the works from Briggs in

(published in 1624) was used instead in the learning activity. According to Lam (2011), Briggs took the square of 2 to get the value of 2², and then took the square again to get 2⁴, 2⁸ and finally multiple the result by 2² to find the value of 2¹⁰. He continued to find the values of 2^{100, 21000} and

x x

Arithmetica Logarithmica

2¹⁰⁰⁰⁰

by the similar way and the result was shown on the table in the fifth

chapter of as below (refer to Figure 8):

Figure 8: The work of Briggs on finding the value of 2¹⁰⁰⁰⁰ Eventually Briggs found that 2100000000000000

is a 30102999566399

-digit number, and it helped him to find a nice approximation of log 2:

2

100000000000000

=

¹⁰30102999566398

(where 1

< 10) log 2100000000000000

=

log ( 1030102999566398

) 100000000000000 log 2

=

^{log + log 10}30102999566398

100000000000000 log 2

=

^log + 30102999566398

log 2

^{= log}

100000000000000+0.30102999566398

log 2

0.30102999566398

This method only involves scientific notation and basic properties of

logarithm, and they are easy to be understood by students. On the other hand, by finding the square root of 10, and then taking square root of the result again and

again … we can get the values of

1

102,

1

104,

1

108^{, …} and use these values to find the approximation of log 2, and it is the method used to create logarithm table in 17^th century (Cho, 2010). The detail is as follows:

1

102 3.16228

,

10¹⁴ 1.77828,

1

108 1.33352,

1

1016 1.15478

1

1032 1.07461,

1

1064 1.03663,

1

10128 1.01815,

1

10256 1.00904

10000

Arithmetica Logarithmica

a a

a a a

a

´ £

´

»

» » » »

» » » »

\

Let 2

¹⁰¹⁴ ₁ then we have

1

1

2

¹⁰4 ^1.1246;

let

1

1 1032 2 then we have

1

2 1 1032 1.04659; let

1

2 1064 3 then we have

1

3 2 1064 1.00961; let

1

3 10256 4 then we have _{4 3} 10²⁵⁶¹ 1.00450; repeating the process to the ^th step and will approach to 1.

Therefore

1 1 1 1 1 1 ⁷⁷

1 1 _...

32 64 256 32 64 256 256

4 4

2

10 10 10 10 ... 10 10

.

And finally we have

77

256 77

log2 log10 0.3

256 .

(Sum up more terms in the series to find a better approximation of log 2.) All the works above had been showed to the students after the activity, and

it seemed that history of mathematics could facilitate a comprehensive

understanding of students in logarithm. Indeed, Fried (2008) states history can

play a part in teaching and learning without altering the focus of our

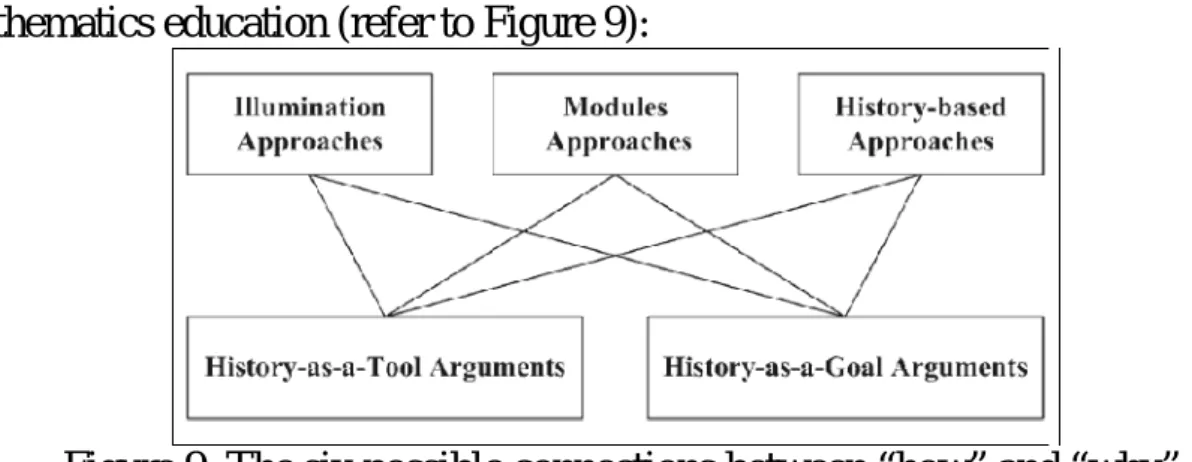
mathematics teaching, and it can be achieved by selecting suitable content from the history. Furthermore, Jankvist (2009) states that the manners in which the history of mathematics may be used in mathematics teaching may be classified into three major categories of approaches:

Illumination approach:

The teaching and learning is supplemented by

historical information. It will be usually appeared

as

“isolated factual information” such as biographies, time charts and famous problems.

Modules approach: The historical content is collected as a package which is narrowly focused on a small topic, with strong ties to the curriculum.

History-based approach:

It includes an account of historical data, a history

of conceptual developments, or something in

between.

Teachers can use different approaches based on their teaching objective:

history-as-a-tool

or

history-as-a-goal (Jankvist, 2009). Obviously history-as-a-tool modules approach had been adopted in the activity. However Jankvist highlights that there is no clear-cut between different approaches and

x x

x x x x

x x x x

x x x x

n xn

= =

= =

= =

= =

+ + + +

= =

=

´ ¸ »

´ ¸ »

´ ¸ »

´ ¸ »

´ ´ ´ ´ »

» »

also there are various combinations of “how” and “why” to use history in

mathematics education (refer to Figure 9):

Figure 9: The six possible connections between “how” and “why”

to use history in mathematics education

By using the above framework, we can obtain a clear vision and aim to apply history in mathematics teaching and learning. On the other hand, Favuel

(1991) states some reasons that have been advanced for using history in

mathematics education, for example:

Helps to increase motivation for learning Gives mathematics a human face

Showing pupils

how

concepts have developed helps their understanding

Changes pupil perceptions of mathematics

Comparing ancient and modern establishes value of modern techniques Provides opportunities for investigations

Pupils derive comfort from realizing that they are not the only ones with problems

Encourages quicker learners to look further

Helps to explain the role of mathematics in society

Can the above advantages be achieved? After the lesson I had asked the students to express their opinions on integrating historical content in learning logarithm. Here are some positive feedbacks from the students (refer to Figure

10). Lot

s

of students pointed out that story of mathematics history was

l l l

l l l l

l l

interesting and help them understand the concept of some topics in mathematics (logarithm in this case). As Favuel mentioned above, history of mathematics can

show how mathematics concepts have developed and hence helps the

understanding of students. At the same time, the attitude of students in learning mathematics has been improved. They showed respect to the mathematicians such as Napier and Briggs and also their works on logarithm, and it motivated students to participate in learning activity proactively.

Figure 10: Some positive feedbacks from students

Meanwhile some negative feedbacks were given (refer to Figure 11). A student pointed out that the method used by Briggs in calculating logarithm was out-of-dated (Indeed Euler had designed an algorithm to find the value of log 2 (Sandifer, 2005), and it was more advanced). Few students also stated that the story of mathematics history was neither related to calculation nor examination.

Figure 11: Some negative feedbacks from students

Actually the negative feedbacks above can be expected. Siu (2007) has pointed out some unfavorable factors to use history in teaching and learning mathematics, such as history of mathematics is not “mathematics”, it cannot improve the student’s grade in tests and examination, and students may not have enough general knowledge on culture to appreciate it. Although there are lots of concerns about using history in teaching mathematics, Siu still believes that integrating mathematics history in teaching and learning can provide a positive reinforcement on the affective side rather than cognitive side of students in mathematics. Actually Siu has already stated the similar point of view:

(Siu 2007, p.276)

For instance, in 1978, Siu has already published a book to encourage

students to study mathematics by referring to the history of mathematics (Siu, 1978). Moreover in 1998, International Commission on Mathematics Instruction (ICMI) has conducted a study on integrating history of mathematics in the classroom, and it was reported by Fauvel and Maanen (2000) which is by far the most comprehensive, extensive and rigorous publication in the field. Their study

provides the framework and positive outcomes of integrating history in

mathematics education.

Last but not least, mathematics is philosophical in its nature, but it does not

mean that we must adopt a philosophical approach for every second in

mathematics classroom. According to the natural way the human minds develop,

“In classes where history of mathematics is made use of, students like the subject more, but they do not necessarily perform better in the tests. One can argue that this may be an indication of a gap between what is taught and learnt and what is being assessed. But still, one cannot deny the possibility that students do not learn better with the addition of a historical dimension.”

Egan (1997) proposes the theory of educated mind with five kinds of

understanding of the human, which are somatic, mythic, romantic, philosophical and ironic. Although the theory of educated mind are based on the study of cultural and linguistic history, Tang (2005, 2006) shows the possibilities of using mathematics history to facilitate different kinds of understanding of

students in mathematics. By using the stories of Napier and Briggs, it can

facilitate students’ romantic understanding in logarithm. The followings are some characteristics of Romantic understanding: 1. the limits of reality and the

extremes of experience; 2. transcendence within reality; 3. humanized

knowledge; and 4. romantic rationality. And the central defining features of romantic understanding are the mixture of the mythic with the rational (Tang, 2006). Recall to the learning activity of logarithm, students had tried and tried again in order to find a better approximation of log 2, log 3 and so on. They learnt the concept and properties of logarithm in a humanized way, and they also experienced in pursuing limit and transcendent qualities. In the activity, the stories and works of Napier and Briggs were presented as “myth” (Napier had spent over 20 years on logarithm, Briggs had found a 30102999566399-digit number to find log 2) rather than “historical facts”, and it can facilitate better

romantic understanding of the students. With the adequate practices, it is

believed that students can proceed to philosophical understanding (including instrumental and relational understanding) in logarithm at the same time.

Usually, there is an overt focus on calculation skills and routine learning, with drills and practice being central to the process of teaching and learning mathematics. However, mathematics is not only consisting of calculation,

problem -solving and logical thinking. As Professor Siu Man Keung states that -

“Mathematics is a cultural heritage”. By exploring the humanistic aspects of

mathematics, it is believed that both students and teachers can appreciate

mathematics as a cultural-human endeavor, broaden the horizon in mathematics

teaching and learning, and finally develop a positive attitude towards

mathematics.

Reference:

Briggs, H. (1624). Arithmetica Logarithmica (Translated by Ian Bruce).

http://www.17centurymaths.com/contents/albriggs.html Egan, K. (1997).

Chicago: The University of Chicago Press.

Fauvel, J. (1991). Using History in Mathematics Education.

, pp. 3-6

Fauvel, J. and Maanen, J.A. (Eds.) (2000),

Netherlands: Kluwer Academic Publishers.

Fried, M.N. (2008). History of Mathematics in Mathematics Education: a Saussurean

Perspective. pp.185-198.

Jankvist, U.T. (2009). A categorization of the “whys” and “hows” of using history in

mathematics education. pp.

235-261.

Katz, V.J. (1986). Using History in Teaching Mathematics.

, pp. 13-19.

Katz,V.J. (1995).

Washington D.C.:Mathematical Association of America.

Sandifer, E. (2005).

.

Washington D.C.:Mathematical Association of America.

Siu, M.K. (1978).

.

Hong Kong: Students’ Time Publication. [In Chinese]

Siu, M.K. (2007).

Uppsala Universitet, pp. 268-277.

Tang, K.C. (2006).

. Iraklion, Greece: University of Crete, pp. 630-638.

(Cho) (2010) -

http://highscope.ch.ntu.edu.tw/wordpress/?p=14488

(Lam) (2011) log 2 52

http://mathcenter.ck.tp.edu.tw/Resources/ePaper/Default.aspx?id=52

The Educated Mind: How Cognitive Tools Shape Our Understanding.

For the Learning of Mathematics, Vol. 11, No. 2

History in Mathematics Education – An ICMI Study.

TheMontanaMathematics Enthusiast, Vol. 5, No. 2,

Educational Studies in Mathematics. Vol. 71,No. 3,

For the Learning of Mathematics, Vol. 6, No. 3 (Nov., 1986)

Napier's logarithmsadapted for today's classroom. In F. Swetz, J. Fauvel, O. Bekken, B. Johansson, & V.Katz(Eds.), Learn from the masters.

Finding Logarithm by Hand. In Sandifer, E. (Eds.). How Euler did it

Why Study Mathematics? Enlightenment from History of Mathematics

No, I don't use history of mathematics in my class. Why?. In F. Furinghetti, S. Kaijser & C. Tzanakis (eds), Proceedings HPM2004 & ESU4, revised ed,

History of Mathematics for the Young Educated Minds: A Hong Kong Reflection. In F. Furinghetti, S. Kaisjer and C. Tzanakis. (Eds.). Proceedings of HPM 2004 & ESU 4 (Revised Edition)

曹亮吉 。《對數表的製作^》。國立台灣大學科學教育發展中心 高瞻自然科學 教學資源平台 。

林倉億 ^。《 怎麼算？^》。教育部高中數學學科中心電子報第 期。台

北：教育部普通高級中學課程數學學科中心。

(Tang) (2005)

鄧國俊 。《初中有向數的教與學：隱喻理論與學養心智理論的啟思^》。黃毅

英主編。《蕭文強教授榮休文集：迎接新世紀重新檢視香港數學教育》。香港：香港 數學教育學會。

Appendix I: The worksheet used in the lesson

Author’s e-mail: patrick_chung@live.com