IEEE PHOTONICS TECHNOLOGY LETTERS, VOL. 23, NO. 12, JUNE 15, 2011 813
Generation of Two-Dimensional Optical Reference
Signals Based on Parametric Minimum Cross Entropy
Yi-Sheng Su, Tsung-Cheng Wu, Chung-Hsuan Wang, and Min-Kuan Chang
Abstract—In this letter, a novel design of two-dimensional (2-D) zero reference codes (ZRCs) based on parametric minimum cross entropy (PMCE) is proposed to generate 2-D optical zero reference signals (ZRSs) with low second maximum for grating alignment systems. An optical ZRS is necessary to obtain an absolute mea-surement in grating alignment systems. A method to acquire an op-tical ZRS is by means of illuminating two idenop-tical superimposed ZRCs. Because the movement between the two ZRCs is in two-axis, 2-D ZRCs are required. However, they are hard to design due to the high computational complexity, especially for large codes. The proposed PMCE method not only reduces the second maximum of 2-D optical ZRSs, but also decreases the computational com-plexity. Simulation results indicate that there are 8.33% 22.22% reductions in the second maximum of several 2-D optical ZRSs, as compared with those of the recently proposed cross-entropy (CE) method. The PMCE method proves to be a powerful tool for the design of 2-D ZRCs.
Index Terms—Autocorrelation function, combinatorial opti-mization, optical position measurement, optimization method, parametric minimum cross entropy (PMCE), two-dimensional (2-D) optical zero reference signal (ZRS), two-dimensional (2-D) zero reference code (ZRC).
I. INTRODUCTION
I
N precision engineering and microtechnology, there is an increasing demand for achieving absolute position, an origin of a coordinate, or a machine home position. To meet the demand, grating alignment systems are widely used. An important component of grating alignment systems is the optical zero reference signal (ZRS). The optical ZRSs are normally obtained by illuminating two identical superimposed zero reference codes (ZRCs). As one ZRC moves with respect to the other, the two codes overlap and the optical ZRS is the autocorrelation of the ZRC transmittance. Because the move-ment is in two-axis, two-dimensional (2-D) ZRCs are required. Based on the properties of autocorrelation, the design of goodManuscript received October 03, 2010; revised January 31, 2011; accepted March 26, 2011. Date of publication April 07, 2011; date of current version May 25, 2011. This work has been supported by the National Science Council (NSC), Taiwan, R.O.C., under Contract NSC-99-2221-E-309-004.
Y.-S. Su is with the Department of Computer Science and Information Engi-neering, Chang Jung Christian University, Tainan City 71101, Taiwan, R.O.C. (e-mail: yssu@mail.cjcu.edu.tw).
T.-C. Wu is with the Department of Communication Engineering, I-Shou University, Kaohsiung City 84001, Taiwan, R.O.C. (e-mail: tcwu@isu.edu.tw). C.-H. Wang is with the Department of Electrical Engineering, National Chiao Tung University, Hsinchu 30010, Taiwan, R.O.C. (e-mail: chwang@mail.nctu. edu.tw).
M.-K. Chang is with the Graduate Institute of Communication Engi-neering, National Chung Hsing University, Taichung, Taiwan, R.O.C. (e-mail: minkuanc@dragon.nchu.edu.tw).
Color versions of one or more of the figures in this letter are available online at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/LPT.2011.2140368
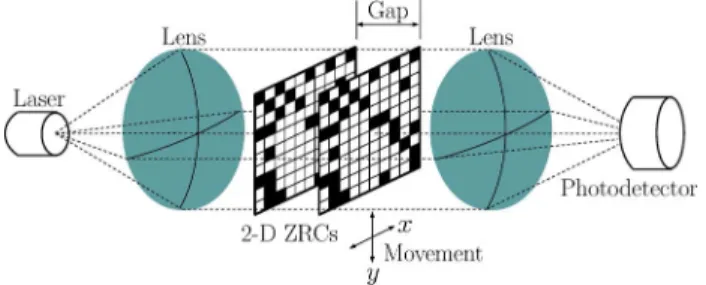
Fig. 1. System for generating 2-D optical ZRSs. Note that it is black outside the 2-D ZRCs.
2-D ZRCs can be modeled as an optimization problem of minimizing the second maximum of the autocorrelation. This problem is related to combinatorial optimization, for which exhaustive search is not feasible due to the high computational complexity.
In recent years, several results have been reported for the de-sign of good 2-D ZRCs [1]–[4]. In [1], a 2-D ZRC with 16 16 elements was presented. In [2], besides calculating a theoret-ical lower bound (LB) for the second maximum, Sáez–Landete
et al. proposed a systematic design method for 2-D ZRCs based
on the DIRECT search algorithm. The algorithm obtains the op-timal solutions only for codes with up to 10 10 elements. To cope with the limitations of [2], a genetic algorithm (GA) with a restricted search operator was proposed in [3]. In [4], motivated by the success of the cross-entropy (CE) method in solving com-plicated, large-scale combinatorial optimization problems, the CE method was proposed to improve upon the design of [3].
In this letter, we propose a novel method to design 2-D ZRCs based on parametric minimum cross entropy (PMCE). The pro-posed method can search for good 2-D ZRCs used for gener-ation of 2-D optical ZRSs. Simulgener-ation results show that this method reduces the second maximum of 2-D optical ZRSs more than the existing schemes, while requiring less computational complexity.
II. PROBLEMFORMULATION
The studied system for generating 2-D optical ZRSs is shown in Fig. 1. The system consists of two opposite identical 2-D ZRCs, at least one of which is set in an movable stage. The 2-D ZRC is a group of unequally spaced transparent and opaque pixels. To acquire a 2-D optical ZRS, a parallel ray beam prop-agates through both codes in the perpendicular direction. The optical output signal (to be registered by means of a photode-tector) is the 2-D optical ZRS and is the correlation between the two 2-D ZRCs, which is a function of the relative displacements along the and directions of the 2-D ZRC. In this letter, as
814 IEEE PHOTONICS TECHNOLOGY LETTERS, VOL. 23, NO. 12, JUNE 15, 2011
assumed in [2]–[4], we do not consider other imperfect factors such as diffraction.1
In general, a 2-D ZRC with elements can be described
by a square matrix of binary data, ,
, with the constraint , where
is the number of transparent pixels, if a trans-parent pixel is located at the position, and else-where. The design of a good 2-D ZRC generally depends on the properties of autocorrelation signal, which is defined as
, ,
where and are the relative displacement units in the and directions, respectively. Clearly,
is the signal obtained when the relative displacement between 2-D ZRCs is zero, and is the maximum value of the autocorrelation signal among all combinations of and . On the other hand, the second maximum of the
auto-correlation signal is . Ideally, a
good 2-D optical ZRS must be a single and well-distinct peak. Accordingly, we can use the ratio between the first and second
maxima, , to characterize ZRSs.
The higher the value of , the better the ZRS.
Typically, the diameter of the light beam propagating through both codes limits the number of pixels in a 2-D ZRC, while the sensitivity of the photodetection optoelectronics determines the minimum value for the first maximum of the signal. Therefore, in accord with these working requirements, we have and predetermined. It turns out that, in order to generate 2-D optical ZRSs with higher , we have to minimize the second maximum of the autocorrelation signal. Thus, the problem of designing good 2-D optical ZRSs is stated as follows:
(1) III. DESIGNMETHODOLOGY
In this section, the PMCE method, which was first proposed by Rubinstein and Dolgin [6] for solving rare event probability estimation and counting problems, is used to design 2-D ZRCs. It is a parametric method for solving the well known Kullback Minimum Cross-Entropy problem. Similar to CE method, the PMCE algorithm first associates the original deterministic opti-mization problem with a relevant rare-event probability estima-tion, and then, in order to estimate efficiently the desired quan-tity, it finds the optimal parameters of the importance sampling distribution. For a more thorough discussion of PMCE method, the reader is referred to [6].
As mentioned, in order to solve (1) by using PMCE, we first randomize (1) into an associate rare-event probability estima-tion. To this end, the element of is modeled as an in-dependent Bernoulli random variable with the probability mass 1The diffraction effect may become non-negligible as the number of pixels in
a 2-D ZRC increases. This is because an increase in the number of pixels will make pixels shrink into a smaller size, in which case the pixel size is no longer large compared to the gap between codes and the wavelength of the illuminating light [5]. The focus of our work is to introduce an efficient PMCE method to minimize the second maximum of 2-D optical ZRS under the same scenario as previous work. The design to include diffraction goes beyond the scope of this work.
function , ,
. Then the probability distribution of is
, where .
We then associate (1) with the problem of estimating the proba-bility for a given second maximum threshold . The basic idea of PMCE algorithm is to iteratively generate the sequences and ( denotes the iteration index), which converge, respectively, to the optimal and in the sense of minimum cross entropy. The optimal can then be obtained from by . Next, we elaborate the step-by-step pro-cedure of the proposed PMCE algorithm as follows:
1) Set and initialize the probability matrix
with .
2) Randomly generate samples from
.
3) Compute second maxima for and
sort them in an increasing order so that
. Set , where
and is the ceiling function.
4) Evaluate with
(2)
where is the indicator of the event that the element of , denoted by , is equal to 1 and the parameter can be obtained from the solution of the fol-lowing equation
(3)
5) Update smoothly via where
is called a smoothing parameter.
6) Output the optimal if the predefined number of itera-tions is reached. Otherwise, increase by 1 and return to Step 2.
Remarks
1) In Step 2, we may need to randomly add/remove the neces-sary 1’s to/from the generated samples in order to meet the con-straint on the number of transparent pixels in (1). 2) In Step 4, the entire sample size is used, which is in contrast to CE method, where only the “elite” sample is used. Moreover, we note that (2) is similar to the standard CE heuristic [4, formula (9)] with only one difference: the indicator function in the CE update formula is replaced here by . 3) In Step 5, is updated in a smoothed procedure in order to pre-vent a fast convergence to a local optimum.
IV. SIMULATIONRESULTS ANDDISCUSSION
In this section, some simulated performance of the proposed PMCE algorithm is presented and compared with that of several other methods [1]–[4]. In the PMCE algorithm, the total number
SU et al.: GENERATION OF 2-D OPTICAL REFERENCE SIGNALS BASED ON PMCE 815
TABLE I
COMPARISON OFSECONDMAXIMA OBTAINED BYDIFFERENTMETHODS AND THECORRESPONDINGRATIO BETWEEN THEFIRST ANDSECONDMAXIMA
SHOWN INPARENTHESIS. DATA ISREPRESENTED IN THEFORM OF ( ). A DASHMEANSTHAT THECORRESPONDINGDATA ISNOTAVAILABLE
Fig. 2. 2-D ZRCs: (a) System 1; (b) System 2; (c) System 3; (d) System 4. TABLE II
COMPARISON OFCOMPUTATIONALCOMPLEXITYBETWEENCEANDPMCE METHODS FORSEARCHING A2-D ZRC WITH AGIVENSECONDMAXIMUM
THRESHOLD. HERE, AVERAGETIME AVERAGETIMEPERITERATION
AVERAGENUMBER OFITERATIONS
is stopped when the iteration number exceeds 500. For compar-ison with [4], four grating alignment systems with different 2-D ZRCs are considered: System 1 ( , ), System
2 ( , ), System 3 ( , ), and
System 4 ( , ).2
Table I shows the second maxima obtained by different methods and the corresponding ratio between the first and second maxima. As seen from Table I, the proposed PMCE method has the smallest second maximum, hence, the largest ratio between the first and second maxima, indicating that the 2Another reason for choosing to generate known 2-D ZRCs is explained as
follows: First, recall that determines the first maximum of a 2-D ZRS. Then, given fixed and , one would desire a system employing a 2-D ZRS with lower second maximum, as the robustness and sensitivity of a system depend on the difference between the first and second maxima [3].
PMCE method is superior to existing methods. More specif-ically, we can observe that there are 9.09%, 8.33%, 22.22%, and 13.33% reductions in the second maximum for System 1, System 2, System 3, and System 4, respectively, as compared to that of the CE method. The 2-D ZRCs obtained by the PMCE method for the four systems are depicted in Fig. 2, where each black square represents a transparent pixel. At the present time, because random search cannot possibly yield a 2-D ZRC with second maximum of 11 for System 2, our method would play an important role in the design of good 2-D ZRCs for industrial applications.3
Table II compares computational complexity between CE and PMCE methods for searching a 2-D ZRC with a given second maximum threshold. For each system under considera-tion, the threshold is chosen as the second maximum obtained by the CE method shown in Table I. The search was carried out on an Intel Core 2 Duo CPU clocked at 3.0 GHz, with 4 GB of physical memory. The results presented are mean values of 100 simulation runs. Table II reveals that, for all four systems, the PMCE method has longer average time per iteration than the CE method due both to using the entire sample size to update (2) and to the need of solving (3). However, the average (searching) time of the PMCE method is still lower than that of the CE method. This is because the PMCE method requires much fewer iterations compared to the CE method.
V. CONCLUSION
In this letter, we proposed a PMCE-based algorithm that was used to minimize the second maximum of the autocorrelation signal of 2-D ZRCs. Simulation results showed that our method outperforms the existing methods, while requiring less com-putational complexity. More specifically, it was observed that there are 8.33% 22.22% reductions in the second maximum of several 2-D optical ZRSs, as compared with those of the CE method. The PMCE method has been demonstrated to be a suit-able technique to the design of 2-D ZRCs.
REFERENCES
[1] Y. Chen, W. Huang, and X. Dang, “Design and analysis of two dimen-sional zero-reference marks for alignment systems,” Rev. Sci. Instrum., vol. 74, no. 7, pp. 3549–3553, 2003.
[2] J. Sáez-Landete, J. Alonso, and E. Bernabeu, “Design of twodimen-sional zero reference codes by means of a global optimization method,”
Opt. Express, vol. 13, no. 11, pp. 4230–4236, 2005.
[3] J. Sáez-Landete, S. Salcedo-Sanz, M. Rosa-Zurera, J. Eusebio, and A. Bernabeu, “Design of two-dimensional zero reference codes with a ge-netic algorithm,” Opt. Lett., vol. 31, no. 11, pp. 1648–1650, 2006. [4] J. Chen, “Design of two-dimensional zero reference codes with
cross-entropy method,” Appl. Opt., vol. 49, no. 18, pp. 3560–3565, 2010. [5] J. Sáez-Landete, S. Salcedo-Sanz, F. Cruz-Roldán, P. Amo-López, and
M. Blanco-Velasco, “Design of two-dimensional optical alignment sig-nals robust to diffractive effects,” J. Lightw. Technol., vol. 26, no. 12, pp. 1702–1707, Jun. 15, 2008.
[6] R. Y. Rubinstein and A. Dolgin, Fast Parametric Entropy-Based and the Parametric MinxEnt Method for Counting of #P-Complete Prob-lems 2007 [Online]. Available: http://www2.technion.ac.il/~heuristics/ downloads/minxent-andrey.pdf
3A reviewer has pointed out that, currently for System 2, the second
max-imum of 14 is easily achievable by a 2-min random search and a 12-h random search can yield a 2-D ZRC with second maximum of 12, but it is not possible to achieve the second maximum of 11 with random search.